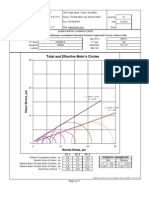
Lecture 6 Stress Path

Given: Figures 1 and 2

Required: Verify that stress paths A, B, and C of Fig.1, and A and D of Fig. 2 are correct as shown.

Solution: The initial conditions for all stress paths in Fig.1 are p = (v + h ) / 2 = v = h and q = 0. Final conditions are following equations:

For stress path A, v = h ; so

Thus the stress path A moves out on the p-axis by an amount v= h , For stress path B, v = h / 2 ; so

These values are the (p,q) coordinates of the end of stress path B. Thus the q and p both increase by an amount q = v /4 and p = 3/4 v , which means that the stress path has a slope of 1/3 or is inclined at 18.4 as shown in Fig.1. For stress path C, h = 0 and v increases by some amount.

So q = v /2 and p = v / 2. Therefore the slope of the stress path must be 1 or inclined at 45. his solution also holds for stress path A in Fig. 2. Here initial conditions are nonhydrostatic, so

The final coordinates for path A are

So q = v /2 and p = v / 2, which is the same as for stress path C in Fig.1. For stress path D in Fig. 2, v decreases while h increases. Initial ( po , q o ) are the same as path A in this figure, while the final values of ( pf , q f ) are

The actual slope of the stress path depends on the relative magnitudes of v and h , but in general it trends down and out as shown in Fig. 2.