The Nine Trigonometric Functions

Kristen Lidwell 10C Mrs. Dewey FST MMSTC

Lidwell 2 There are nine trigonometric functions, which are all based off of three original functions: cosine, sine, and tangent. The other six functions are just the original functions inverses and reciprocals. Trigonometric functions are based off of the unit circle, since the different angles and coordinates are used in the different functions. Trigonometry relates to triangles, their angles, and their sides, so it ma es sense that trigonometric functions can be used in right triangle trigonometry aside from being used as just functions. Though nine functions may seem li e a lot, each function is just a different variation of the other.

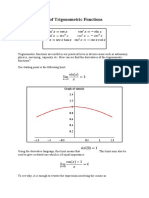
!igure ". #raph of the $osine, %nverse $osine, and &ecant !unctions

The graphs above shows the three different functions relating to the original trigonometric function, cosine. !irst is the graph of cosine, then its inverse, and then its reciprocal, secant. The first original function is the cosine function, shown in the first graph in !igure ". The cosine function is based off of the x'coordinates of points on the unit circle, such as ", ()*2, (2*2, "*2, +, continuing around the circle. ,hen an angle measure is put in as x, in y-cos.x/, the output will be its x'coordinate on the unit circle for that angle measure. The values repeat periodically as the function continues, ma ing the cosine function continuous. $osine has no

Lidwell ) asymptotes, which are lines indicating where the graph cannot touch since it would be undefined.

The period is 2 radians, which mean that for every 2 of the x'coordinates, the y'coordinates

repeat themselves. This means the fre0uency of the function is "* 2 , meaning one cycle is 2 long. The cosine function is an even function, which means it has symmetry to the y'axis. The domain of the cosine function is which symboli1es that the x'values are an element of all real numbers, and it has a range of '" 2 y 2 ". The cosine function has y'intercept of .+,"/, which is also the maximum of the function. The minimum of the cosine function is '". The x'intercepts

occur at odd multiples of

3 variation of the cosine function is the inverse cosine function, which is shown graphically in !igure "s second graph. 3s all inverses, the function is reflected over the y-x line, and the domain and range are switched from the original function of cosine. &ince a function cannot have more than one output for each input the range of the inverse cosine function

must be restricted to + 2 y 2 . The domain of inverse cosine, however, does not need to be restricted and is the same as the range of the cosine function, '" 2 x 2 ". The inverse cosine function is neither odd, nor even, and is not continuous due to the range restriction. The inverse cosine does not have a fre0uency or period since it does not repeat. ,hen a coordinate from unit circle is put in as x in y-cos'".x/, the output will be the angle measure that goes with that coordinate.

Lidwell 4 The final variation of cosine is the reciprocal, or secant function, shown in !igure "s third graph. The graph shows the secant function in red and how it relates to the original cosine function in blue. This function is y- sec.x/, but can also be pictured as y- "*cos.x/, since it is a reciprocal. &ince it is a math rule that one cannot divide by 1ero, this function has asymptotes wherever the output of y- cos.x/ is 1ero. This means since the original cosine function has x'

intercepts at odd multiples of

, the secant function has vertical asymptotes there. The only

places where the secant function intersects the original cosine are when the original cosine functions has maximums at ", or minimums at '". The domain of this function is except for

odd multiples of

, and the range is y5" or y2 '". The secant function is not continuous due to

its asymptotes, but it is even and has a period of 2 li e the original cosine function.

!igure 2. #raph of the &ine, %nverse &ine, and $osecant !unctions

The graphs above show the three different functions relating to the original trigonometric function, sine. !irst is the graph of sine, then its inverse, then its reciprocal, cosecant.

Lidwell 6 The next original trigonometric function is the sine function, shown in the first graph in

!igure 2. Li e the cosine function, it is continuous, has a period of 2 , a fre0uency of "*

,a

maximum y'value of ", a minimum y'value of '", and no asymptotes. 3lso, the cosine and sine functions have the same domain of , and range of '" 2 y 2 ".7nli e the cosine function though, the sine function is based off of the y'coordinates of points on the unit circle, such as +, "*2, (2*2, ()*2, and ". ,hen an angle measure is put in as x, in y-sin.x/, the output will be its y' coordinate on the unit circle for that angle measure. 3lso, the sine function is odd, meaning it has rotational symmetry to the origin. The y'intercept of the sine function is .+,+/, and the x'

intercepts occur at integer multiples of

The sine function also has an inverse, shown in !igure 2s second graph. The range of sine also needs to be restricted so it contains all the values of sine without having more than one output per input, so instead of being all real numbers li e the domain of sine, it was restricted to

8 *2 2 y 2 8 *2. The domain matches the cosine inverse function, '" 2 x 2 ". Li e the original sine function, the inverse sine function is odd. The function has no asymptotes, but is not continuous because of its restricted range. ,hen a y'coordinate from unit circle is put in as x in y-sin'".x/, the output will be the angle measure that goes with that coordinate. The reciprocal sine function is the cosecant function, shown in the third graph of !igure 2. The cosecant function is in red, whereas the original sine function is in blue. &ince this function is a reciprocal, it can be thought of as y-"*sin.x/, but as a function it is written out

Lidwell 9 y-csc.x/. ,here the sine function has x'intercepts at integer multiples of , the cosecant function has vertical asymptotes. The cosecant and sine functions intersect at where the sine function has minimums or maximums, at y- " or '". The domain of cosecant is except

integer multiples of , and the range is y 5 " or y 2 '". The cosecant function, li e the sine function, is an odd function. %t is not continuous since the function has the vertical asymptotes.

!igure ). #raph of the Tangent, %nverse Tangent, and $otangent !unctions

The graphs above show the three different functions relating to the original trigonometric function, tangent. !irst is the graph of tangent, then its inverse, and then its reciprocal, cotangent. The final original trigonometric function is tangent, shown in the first graph of !igure ). The tangent function values relate to the slope of the coordinates on the circle, rather than the

coordinates alone. Tangent is y-

, or y-tan.x/. &ince tangent uses the slope of the unit circle

coordinates, rather than just the coordinates, the graphs appearance is much different than of

cosine or sine. The domain of tangent is all real numbers except odd multiples of *2, and the

Lidwell : range is . ,here x- odd multiples of *2, the tangent function has vertical asymptotes, ma ing the function not continuous. The asymptotes are where the value of cosine is 1ero, since

anything divided by 1ero is undefined. The period of tangent is , and a fre0uency of "* , which

means the function repeats faster than cosine or sine, whose periods are

. The tangent function

is odd, has x'intercepts at integer multiples of , and a y'intercept at .+,+/.

The tangent function has an inverse, inverse tangent, shown in the second graph of !igure ). The domain and range of the original tangent are swapped to ma e the inverse, so the inverse tangents domain is . The range is restricted li e the other basic trigonometric functions

inverses so that there is only one output per input, ma ing the range is ' *2 ; y ; *2. 3t y- '

*2 and at y- *2 there are hori1ontal asymptotes, which are tangents vertical asymptotes reflected over the y-x line. The inverse tangent function is odd, and not continuous due to its asymptotes. The y and x'intercept of tangent inverse is .+,+/. ,hen a slope from unit circle is put in as x in y-tan'".x/, the output will be the angle measure that goes with that slope. The reciprocal of the tangent function, cotangent, is shown in the third graph in !igure ).

This function can be thought of as y-

, or y- "*tan.x/, since it is a reciprocal though it is

written as y-cot.x/. ,here the original tangent function had x'intercepts at integers multiples of

Lidwell < , the cotangent function has vertical asymptotes since one cannot divide by 1ero. The x'

intercepts of the cosine function are at odd multiples of *2, where the asymptotes of the original tangent function are. The cotangent function goes in a negative direction and decreases, where

the tangent function is increasing. The period of cotangent is , li e the period of tangent. The

domain of the cotangent function is except integers multiples of , and the range is . The cotangent function is odd, and not continuous.

>pposite

?ypotenuse

3djacent

!igure 4. =ight Triangle

!igure 4 shows a right triangle. Theta is labeled and the sides are labeled in relation to theta.

The nine trigonometric functions can be used in right triangle trigonometry. The functions can be used to either find side lengths, or theta. Theta is the angle measure of the triangle that is either going to be found, or used to find a side length. The diagonal side of the

Lidwell @ triangle is the hypotenuse, the side next to theta is the adjacent side, and the side opposite to theta is the adjacent side. The original trigonometric functions are used to find different side lengths of the triangle. The term &oh$ahToa is used to help remember the ratios of the triangle sides used to find an un nown side. The sine function uses the &oh, which stands for sine of theta e0uals the opposite

side of the triangle over the hypotenuse, and is written as sin =

. ,hen given the

theta and either the opposite side or hypotenuse, by using into the e0uation it is possible to find the un nown side length. The cosine function uses the $ah, which stands for cosine of theta

e0uals the adjacent side over the hypotenuse, and is written as cos =

. ,hen given

the theta and either the adjacent side or the hypotenuse, by plugging what is nown into the e0uation it is possible to find the un nown side length. The Toa is used for tangent, which stands

for tangent of theta e0uals opposite side over adjacent side, written as tan =

. ,hen

given the theta and an opposite or adjacent side of a right triangle, one can use tangent to find the other un nown length. The reciprocal functions are also used to find side lengths as well. The fraction used to find the side is flipped from the original trigonometric function. To find a side using cosecant,

Lidwell "+ one would use cotangent of theta e0uals the hypotenuse over the opposite side, written as csc =

, which is the reciprocal of sin =

. &ecant of theta is the triangles

hypotenuse over the adjacent side, which is written as sec=

, the reciprocal of

cos =

. $otangent of theta is the adjacent side over the opposite side, written as

cot =

, which is the reciprocal of tan =

. ,hen given a side length and theta,

either the reciprocal or the original trigonometric function can be used to find the un nown side. Aepending on which side is given though, the choice of which function can result in less mathematical error when solving. The inverse functions are used to find the measure of theta in right triangle trigonometry. The angle measure is found by ta ing the inverse of the trigonometric ratios used to find the side length, to solve for theta, instead of a side. %nverse sine is used to find theta when given the opposite side and the hypotenuse. The measure of theta is found by doing the inverse sine of the

opposite side over the hypotenuse, written as = sin'"(

). %nverse cosine is used when

finding thetas angle measure when given thetas adjacent side and the hypotenuse. To find the

Lidwell "" angle measure, one does the inverse cosine of the adjacent side over the hypotenuse, which is

written as = cos 1(

). %nverse tangent is used when trying to find theta when given

thetas opposite and adjacent side. To get the measure of theta, calculate the inverse tangent of

the opposite side over the adjacent side, which is written as tan = tan'".

/. Aepending on

the information given, inverse trigonometric functions can be very useful in find angle measures of a right triangle. 3ll in all, the nine different trigonometric are not very different from each other. The inverse and reciprocal functions should just be thought of as variations of cosine, sine, and tangent. Trigonometric functions have a variety of uses, including the unit circle, graphs, right triangles, and even real life applications. $osine and sine functions can be used to model real life periodic data, such as yearly temperatures. %f there is ever a right triangle with an un nown side, or a trigonometric graph that needs identification, there are nine trigonometric functions that will help get the job done.