Académique Documents
Professionnel Documents
Culture Documents
Fluid Mechanics: Edgar Buckingham J. Bertrand Rayleigh
Transféré par
km_ananth0 évaluation0% ont trouvé ce document utile (0 vote)
17 vues1 pageThe π theorem, which describes the relationship between physical quantities based on their dimensions, was first proved by French mathematician J. Bertrand in 1878, although it is named for Edgar Buckingham. Bertrand considered special cases in electrodynamics and heat conduction. The technique became widely known due to works by Lord Rayleigh in the 1890s. Formal generalization of the theorem for arbitrarily many quantities was given by Vaschy in 1892 and independently by Federman and Riabouchinsky in 1911. It was Buckingham who introduced using "πi" for the dimensionless variables and whose 1914 article gave the theorem its name.
Description originale:
liquids
Titre original
Pi Theorem
Copyright
© © All Rights Reserved
Formats disponibles
DOCX, PDF, TXT ou lisez en ligne sur Scribd
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentThe π theorem, which describes the relationship between physical quantities based on their dimensions, was first proved by French mathematician J. Bertrand in 1878, although it is named for Edgar Buckingham. Bertrand considered special cases in electrodynamics and heat conduction. The technique became widely known due to works by Lord Rayleigh in the 1890s. Formal generalization of the theorem for arbitrarily many quantities was given by Vaschy in 1892 and independently by Federman and Riabouchinsky in 1911. It was Buckingham who introduced using "πi" for the dimensionless variables and whose 1914 article gave the theorem its name.
Droits d'auteur :
© All Rights Reserved
Formats disponibles
Téléchargez comme DOCX, PDF, TXT ou lisez en ligne sur Scribd
0 évaluation0% ont trouvé ce document utile (0 vote)
17 vues1 pageFluid Mechanics: Edgar Buckingham J. Bertrand Rayleigh
Transféré par
km_ananthThe π theorem, which describes the relationship between physical quantities based on their dimensions, was first proved by French mathematician J. Bertrand in 1878, although it is named for Edgar Buckingham. Bertrand considered special cases in electrodynamics and heat conduction. The technique became widely known due to works by Lord Rayleigh in the 1890s. Formal generalization of the theorem for arbitrarily many quantities was given by Vaschy in 1892 and independently by Federman and Riabouchinsky in 1911. It was Buckingham who introduced using "πi" for the dimensionless variables and whose 1914 article gave the theorem its name.
Droits d'auteur :
© All Rights Reserved
Formats disponibles
Téléchargez comme DOCX, PDF, TXT ou lisez en ligne sur Scribd
Vous êtes sur la page 1sur 1
Although named for Edgar Buckingham, the theorem was first proved by French mathematician J. Bertrand[1] in 1878.
. Bertrand considered only special cases of problems
from electrodynamics and heat conduction, but his article contains in distinct terms all the basic ideas of the modern proof of the theorem and clear indication of its utility for
modelling physical phenomena. The technique of using the theorem (the method of dimensions) became widely known due to the works of Rayleigh (the first application of
the theorem in the general case[2] to the dependence of pressure drop in a pipe upon governing parameters probably dates back to 1892, [3] a heuristic proof with the use of
series expansion, to 1894[4]).
Formal generalization of the theorem for the case of arbitrarily many quantities was given first by A. Vaschy in 1892, [5] then in 1911apparently independentlyby both A.
Federman,[6] and D. Riabouchinsky,[7] and again in 1914 by Buckingham. [8] It was Buckingham's article that introduced the use of the symbol "i" for the dimensionless variables
(or parameters), and this is the source for the theorem's name.
Fluid Mechanics[edit]
Common dimensionless groups in fluid mechanics include:
Reynolds number (Re) generally important in all types of fluid problems.
Re = Vd/
Froude number (Fr) modeling flow with a free surface.
Fr = V/(gL)
Euler number (Eu) used in problems in which pressure is of interest.
Eu = V/(p/)
Vous aimerez peut-être aussi
- MANNING Robert: Short Historical Dictionary On Urban Hydrology and DrainageDocument11 pagesMANNING Robert: Short Historical Dictionary On Urban Hydrology and Drainagewilsonwong71Pas encore d'évaluation
- (Boston Studies in The Philosophy of Science 277) Paul Needham (Auth.), Paul Needham (Eds.) - Commentary On The Principles of Thermodynamics by Pierre Duhem-Springer Netherlands (2011)Document232 pages(Boston Studies in The Philosophy of Science 277) Paul Needham (Auth.), Paul Needham (Eds.) - Commentary On The Principles of Thermodynamics by Pierre Duhem-Springer Netherlands (2011)PedroPas encore d'évaluation
- Thermodynamics - WikipediaDocument13 pagesThermodynamics - WikipediaDanie ElsPas encore d'évaluation
- Pyrometry: A Practical Treatise on the Measurement of High TemperaturesD'EverandPyrometry: A Practical Treatise on the Measurement of High TemperaturesPas encore d'évaluation
- ThermodynamicsDocument14 pagesThermodynamicsdanny222Pas encore d'évaluation
- On Formally Undecidable Propositions of Principia Mathematica and Related SystemsD'EverandOn Formally Undecidable Propositions of Principia Mathematica and Related SystemsÉvaluation : 4.5 sur 5 étoiles4.5/5 (26)
- Hermodynamics Is The Branch Of: System SurroundingsDocument8 pagesHermodynamics Is The Branch Of: System SurroundingsDamisha DamishaPas encore d'évaluation
- G. N. Lewis 2' PDFDocument8 pagesG. N. Lewis 2' PDFivasiton0% (1)
- Thermodynamics - WikipediaDocument15 pagesThermodynamics - Wikipediapsri1944Pas encore d'évaluation
- ThermodynamicsDocument15 pagesThermodynamicspsri1944Pas encore d'évaluation
- Thermodynamics - WikipediaDocument15 pagesThermodynamics - Wikipediapsri1944Pas encore d'évaluation
- ThermdynamcsDocument13 pagesThermdynamcsTejas krishnakanthPas encore d'évaluation
- ThermodynamicsDocument14 pagesThermodynamicsEurich EstradaPas encore d'évaluation
- SwissDocument8 pagesSwissRajaram RamanPas encore d'évaluation
- Thermodynamics Is The Branch ofDocument2 pagesThermodynamics Is The Branch ofbennyPas encore d'évaluation
- Thermodynamics Is A Branch Of: (Hide)Document5 pagesThermodynamics Is A Branch Of: (Hide)ksrm123Pas encore d'évaluation
- History: Georg Ohm Henry Cavendish Leyden JarsDocument4 pagesHistory: Georg Ohm Henry Cavendish Leyden JarsIMBAJOEPas encore d'évaluation
- Entropy: The Gibbs Paradox: Early History and SolutionsDocument54 pagesEntropy: The Gibbs Paradox: Early History and SolutionsNina RiveroPas encore d'évaluation
- Thermodynamics - WikipediaDocument78 pagesThermodynamics - WikipediasubhajitparichhaPas encore d'évaluation
- Team ThermalDocument11 pagesTeam ThermalDamisha DamishaPas encore d'évaluation
- Famous PhysicistsDocument4 pagesFamous PhysicistsJannet De Lara VergeldeDiosPas encore d'évaluation
- Thermodynamics: Thermodynamics Is A Branch of Physics Concerned With Heat andDocument10 pagesThermodynamics: Thermodynamics Is A Branch of Physics Concerned With Heat andJayaPas encore d'évaluation
- Thermodynamics 101 - 2Document2 pagesThermodynamics 101 - 2Joseph DustPas encore d'évaluation
- 1.1 Preliminary Semantics: Read BS, Chapter 1Document18 pages1.1 Preliminary Semantics: Read BS, Chapter 1Palash KanjilalPas encore d'évaluation
- Chapter 1Document18 pagesChapter 1M Sigit A MaskarebetPas encore d'évaluation
- Famous Physicist: Sir Isaac Newton (1642-1727)Document7 pagesFamous Physicist: Sir Isaac Newton (1642-1727)babymowsPas encore d'évaluation
- History of HeatDocument31 pagesHistory of Heatkarlo marko sta. rosaPas encore d'évaluation
- Chemical Engineering Nobel Prize William Ramsay Prize in Chemistry Noble Gases E. C. WilliamDocument1 pageChemical Engineering Nobel Prize William Ramsay Prize in Chemistry Noble Gases E. C. WilliamJolteon JuniorPas encore d'évaluation
- HT MT Dimensionaless NumbersDocument14 pagesHT MT Dimensionaless Numbersvirender_ajaykumarPas encore d'évaluation
- Constantin Carathéodory and The Axiomatic ThermodynamicsDocument12 pagesConstantin Carathéodory and The Axiomatic ThermodynamicsajejeyPas encore d'évaluation
- Gas ConstantDocument2 pagesGas Constantmechanical15Pas encore d'évaluation
- Richard Becker (Auth.) - Theory of Heat-Springer Berlin Heidelberg (1967) PDFDocument393 pagesRichard Becker (Auth.) - Theory of Heat-Springer Berlin Heidelberg (1967) PDFJulian SierraPas encore d'évaluation
- Notes PHY3Document3 pagesNotes PHY3Ako ToPas encore d'évaluation
- Chapter 2 - History of Dimensional AnalysisDocument7 pagesChapter 2 - History of Dimensional AnalysisShaikh Abdur RazzakPas encore d'évaluation
- Famous Physicis-WPS OfficeDocument6 pagesFamous Physicis-WPS OfficeAbhishek B Kumar VfcPas encore d'évaluation
- History and Outlook of Statistical PhysicsDocument13 pagesHistory and Outlook of Statistical PhysicsWritobroto MukhopadhyayPas encore d'évaluation
- Mie ScatteringDocument20 pagesMie Scatteringismake31Pas encore d'évaluation
- William Gilbert Robert HookeDocument3 pagesWilliam Gilbert Robert HookeJan Alan RosimoPas encore d'évaluation
- Duisburg Utrecht Leiden Mathematics Astronomy Capacitor Leyden JarDocument7 pagesDuisburg Utrecht Leiden Mathematics Astronomy Capacitor Leyden JarMarvin GagarinPas encore d'évaluation
- Paneth, Kant, and The Philosophy of Chemistry (Ruthenberg, 2009) .Document13 pagesPaneth, Kant, and The Philosophy of Chemistry (Ruthenberg, 2009) .Eduardo AndresPas encore d'évaluation
- 81 KraghDocument37 pages81 KraghLeonPas encore d'évaluation
- A History of ThermodynamicsDocument48 pagesA History of Thermodynamicsهند صلاح الدينPas encore d'évaluation
- The Use and Misuse of The Word Heat in Physics TeachingDocument6 pagesThe Use and Misuse of The Word Heat in Physics Teaching이천호Pas encore d'évaluation
- Schrödinger and Dirac Equations For The Hydrogen Atom, and Laguerre PolynomialsDocument34 pagesSchrödinger and Dirac Equations For The Hydrogen Atom, and Laguerre Polynomialsecd4282003Pas encore d'évaluation
- EinsteinDocument1 pageEinsteinarghya_bi108Pas encore d'évaluation
- Christian Hülsmeyer and About The Early Days of Radar InventionsDocument74 pagesChristian Hülsmeyer and About The Early Days of Radar InventionsAndrei NecuţăPas encore d'évaluation
- Thermodynamics: Eastern Visayas State University Carigara CampusDocument14 pagesThermodynamics: Eastern Visayas State University Carigara CampusJordam Ian LabacladoPas encore d'évaluation
- Introduction, History and Applications: Engr. Shakeel AhmadDocument13 pagesIntroduction, History and Applications: Engr. Shakeel AhmadShakeel MohmandPas encore d'évaluation
- Amedeo AvogadroDocument4 pagesAmedeo AvogadroEnriquez JohnPas encore d'évaluation
- Amedeo AvogadroDocument4 pagesAmedeo AvogadroEnriquez JohnPas encore d'évaluation
- Amedeo AvogadroDocument4 pagesAmedeo AvogadroEnriquez JohnPas encore d'évaluation
- Heisler Chart - WikipediaDocument5 pagesHeisler Chart - WikipediaRaja KarthiPas encore d'évaluation
- Gas LawsDocument20 pagesGas LawsDavidPas encore d'évaluation
- Timeline of ThermodynamicsDocument4 pagesTimeline of ThermodynamicsBob JoePas encore d'évaluation
- Thermodynamics Is The Science Of: o o o o oDocument15 pagesThermodynamics Is The Science Of: o o o o oPratik YadavPas encore d'évaluation
- ThermodynamicsDocument8 pagesThermodynamicsec0nomistPas encore d'évaluation
- Scientist HistoryDocument3 pagesScientist Historyafzal786435Pas encore d'évaluation
- Fe250 Fe415 Fe500: SC N/SQMMDocument2 pagesFe250 Fe415 Fe500: SC N/SQMMkm_ananthPas encore d'évaluation
- Muruganantham.m Plot-15, Mannar Maruthu Pandiar Nagar, Nagai Road, ThanjavurDocument1 pageMuruganantham.m Plot-15, Mannar Maruthu Pandiar Nagar, Nagai Road, Thanjavurkm_ananthPas encore d'évaluation
- VasthuDocument4 pagesVasthuRaja ManiPas encore d'évaluation
- Cure For Autoimmune DisordersDocument1 pageCure For Autoimmune Disorderskm_ananthPas encore d'évaluation
- Proposed Residence For MR - Asraf, Kumbakonam.: Ward RobeDocument1 pageProposed Residence For MR - Asraf, Kumbakonam.: Ward Robekm_ananthPas encore d'évaluation
- The Lord Buddha'S Breathing Techniques & MeditationDocument3 pagesThe Lord Buddha'S Breathing Techniques & Meditationkm_ananthPas encore d'évaluation
- Weight Calculation For GuruvayurDocument2 pagesWeight Calculation For Guruvayurkm_ananthPas encore d'évaluation
- TedaDocument1 pageTedakm_ananthPas encore d'évaluation
- Another Symbol Is The Lightning BoltDocument17 pagesAnother Symbol Is The Lightning Boltkm_ananthPas encore d'évaluation
- Cure For InfertilityDocument8 pagesCure For Infertilitykm_ananthPas encore d'évaluation
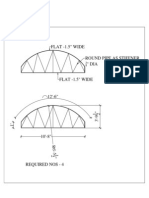
- Arch TemplateDocument1 pageArch Templatekm_ananthPas encore d'évaluation
- Cure For Urinary ProblemsDocument2 pagesCure For Urinary Problemskm_ananthPas encore d'évaluation
- Arch DesignDocument5 pagesArch Designkm_ananthPas encore d'évaluation
- Cure For Bipolar DisorderDocument5 pagesCure For Bipolar Disorderkm_ananthPas encore d'évaluation
- AstroDocument4 pagesAstrokm_ananthPas encore d'évaluation
- Accu PointDocument8 pagesAccu Pointkm_ananthPas encore d'évaluation
- Magical HerbDocument17 pagesMagical Herbkm_ananth100% (1)
- Care For MigraineDocument5 pagesCare For Migrainekm_ananthPas encore d'évaluation
- Strip Footing DesignDocument4 pagesStrip Footing Designkm_ananth100% (1)
- Big TempleDocument10 pagesBig Templekm_ananthPas encore d'évaluation
- Care For MigraineDocument5 pagesCare For Migrainekm_ananthPas encore d'évaluation
- Strip Footing DesignDocument4 pagesStrip Footing Designkm_ananth100% (1)
- Care For MigraineDocument5 pagesCare For Migrainekm_ananthPas encore d'évaluation
- Strip Footing DesignDocument4 pagesStrip Footing Designkm_ananth100% (1)
- Ayur MedicinesDocument21 pagesAyur Medicineskm_ananth100% (1)
- Guidelines Bridge DesignDocument208 pagesGuidelines Bridge Designaa19100% (13)
- STAAD Design Parameter GeneratorDocument48 pagesSTAAD Design Parameter GeneratorjaffnaPas encore d'évaluation
- Hybrid Solar System V1.01Document21 pagesHybrid Solar System V1.01km_ananthPas encore d'évaluation
- AutoCAD CommandsDocument47 pagesAutoCAD Commandskm_ananthPas encore d'évaluation
- ParaPro Assessment Preparation 2023-2024: Study Guide with 300 Practice Questions and Answers for the ETS Praxis Test (Paraprofessional Exam Prep)D'EverandParaPro Assessment Preparation 2023-2024: Study Guide with 300 Practice Questions and Answers for the ETS Praxis Test (Paraprofessional Exam Prep)Pas encore d'évaluation
- Basic Math & Pre-Algebra Workbook For Dummies with Online PracticeD'EverandBasic Math & Pre-Algebra Workbook For Dummies with Online PracticeÉvaluation : 4 sur 5 étoiles4/5 (2)
- Build a Mathematical Mind - Even If You Think You Can't Have One: Become a Pattern Detective. Boost Your Critical and Logical Thinking Skills.D'EverandBuild a Mathematical Mind - Even If You Think You Can't Have One: Become a Pattern Detective. Boost Your Critical and Logical Thinking Skills.Évaluation : 5 sur 5 étoiles5/5 (1)
- Quantum Physics: A Beginners Guide to How Quantum Physics Affects Everything around UsD'EverandQuantum Physics: A Beginners Guide to How Quantum Physics Affects Everything around UsÉvaluation : 4.5 sur 5 étoiles4.5/5 (3)
- Images of Mathematics Viewed Through Number, Algebra, and GeometryD'EverandImages of Mathematics Viewed Through Number, Algebra, and GeometryPas encore d'évaluation
- Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative TeachingD'EverandMathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative TeachingÉvaluation : 4.5 sur 5 étoiles4.5/5 (21)
- Calculus Workbook For Dummies with Online PracticeD'EverandCalculus Workbook For Dummies with Online PracticeÉvaluation : 3.5 sur 5 étoiles3.5/5 (8)
- Fluent in 3 Months: How Anyone at Any Age Can Learn to Speak Any Language from Anywhere in the WorldD'EverandFluent in 3 Months: How Anyone at Any Age Can Learn to Speak Any Language from Anywhere in the WorldÉvaluation : 3 sur 5 étoiles3/5 (79)
- Mental Math: How to Develop a Mind for Numbers, Rapid Calculations and Creative Math Tricks (Including Special Speed Math for SAT, GMAT and GRE Students)D'EverandMental Math: How to Develop a Mind for Numbers, Rapid Calculations and Creative Math Tricks (Including Special Speed Math for SAT, GMAT and GRE Students)Pas encore d'évaluation
- Who Tells the Truth?: Collection of Logical Puzzles to Make You ThinkD'EverandWho Tells the Truth?: Collection of Logical Puzzles to Make You ThinkÉvaluation : 5 sur 5 étoiles5/5 (1)
- How Math Explains the World: A Guide to the Power of Numbers, from Car Repair to Modern PhysicsD'EverandHow Math Explains the World: A Guide to the Power of Numbers, from Car Repair to Modern PhysicsÉvaluation : 3.5 sur 5 étoiles3.5/5 (9)
- A Guide to Success with Math: An Interactive Approach to Understanding and Teaching Orton Gillingham MathD'EverandA Guide to Success with Math: An Interactive Approach to Understanding and Teaching Orton Gillingham MathÉvaluation : 5 sur 5 étoiles5/5 (1)
- Transform Your 6-12 Math Class: Digital Age Tools to Spark LearningD'EverandTransform Your 6-12 Math Class: Digital Age Tools to Spark LearningPas encore d'évaluation
- Magic Multiplication: Discover the Ultimate Formula for Fast MultiplicationD'EverandMagic Multiplication: Discover the Ultimate Formula for Fast MultiplicationPas encore d'évaluation