Académique Documents
Professionnel Documents
Culture Documents
Triángulo de Pascal
Transféré par
Daniel BeltránDescription originale:
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Triángulo de Pascal
Transféré par
Daniel BeltránDroits d'auteur :
Formats disponibles
Tringulo de Pascal
De Wikipedia, la enciclopedia libre
Tringulo de Pascal o de Tartaglia El tringulo de Pascal en matemticas es un conjunto infinito de nmeros enteros ordenados en forma de tringulo que expresan coeficientes binomiales. El inters del Tringulo de Pascal radica en su aplicacin en lgebra y permite calcular de forma sencilla nmeros combinatorios lo que sirve para aplicar el binomio de Newton. Tambin es conocido como Tringulo de Tartaglia. En pases no occidentales como China o India, este tringulo se conoca y fue estudiado por matemticos cinco siglos antes de que Pascal expusiera sus aplicaciones. En China es conocido como Tringulo de Yanghui.
Contenido
1 Composicin del Tringulo de Pascal 2 Vnculo entre el tringulo de Pascal y el binomio de Newton 3 Coeficientes del binomio de Newton 4 Interpretacin en combinatoria 5 Generalizacin 6 Otra forma de dibujar el tringulo 7 Enlaces externos
Composicin del Tringulo de Pascal
El Tringulo se construye de la siguiente manera: sobre un papel cuadriculado, escribimos el nmero 1, centrado en la parte superior; despus, escribimos una serie de nmeros 1 en las casillas situadas en sentido diagonal descendente, a ambos lados; sumamos las parejas de cifras situadas horizontalmente y separadas por una casilla en blanco (1 + 1), y el resultado (2) lo escribimos debajo de dicha casilla; continuamos el proceso escribiendo, en las casillas inferiores, la suma de las dos cifras situadas sobre ellas (1 + 2 = 3)...
Las cifras escritas en las filas, tales como: 1 2 1 y 1 3 3 1 recuerdan las identidades:
pues son los coeficientes de sus monomios y, adems, se puede generalizar para cualquier potencia del binomio:
Vnculo entre el tringulo de Pascal y el binomio de Newton
La expresin que proporciona las potencias de una suma de Newton. se denomina Binomio
(1) En esta expresin, lo nico que se desconoce son los coeficientes de los monomios.
Los coeficientes de la forma desarrollada de (a + b)n se encuentran en la lnea n + 1 del Tringulo de Pascal. Hemos visto que era cierto para n = 2 y n = 3; tambin lo es para n = 0: (a + b)o = 1 = 1aob0 y con n = 1: (a + b) = a + b = 1a + 1b. Para obtener el resultado de cualquier valor de n N, se procede por induccin matemtica. Suponiendo que es cierto para un valor de n, deducimos que lo es tambin para n+1. Observemos lo que sucede con n = 4.
El desarrollo de (a + b)4 consiste en el desarrollo de (a + b) (a + b). Si slo se escriben los coeficientes, obtenemos la siguiente suma:
Obviamente, aparecen las mismas cifras desplazadas en una posicin: la suma consiste en aadir a un coeficiente el coeficiente situado a su derecha, y esto es justamente lo que se obtiene en el tringulo de Pascal.
Coeficientes del binomio de Newton
Se inscribe el tringulo de Pascal en una tabla para poder nombrar a cada coeficiente del mismo. El nmero en la lnea n y la columna p se denota:
o ms raramente
("C" por "combinacin") (por ejemplo en calculadoras de bolsillo, como la TI-86 y familia), y se dice "n sobre k", "'combinacin de n en k"' mucho ms corto que "coeficiente binomial n, k". Las casillas vacas corresponden a valores nulos. Por definicin misma, tenemos, (para todo n natural):
para cualquier valor de a y b. De hecho, es una igualdad de polinomios en Z[a, b]. Sin perder en generalidad, resulta a veces ms prctica la "definicin" :
vista como una igualdad de polinomios en Z[X]. De esta frmula se deducen dos consecuencias:
Tomando X = 1 se obtiene: La suma de los coeficientes de una misma lnea vale 2n. En efecto: 1 = 20, 1 + 1 = 2 = 2, 1 + 2 + 1 = 4 = 2, 1 + 3 + 3 + 1 = 8 = 2, 1 + 4 + 6 + 4 + 1 = 16 = 24 ... Con X = -1 se obtiene, (n > 0):
: la suma alterna de los nmeros de una misma lnea vale 0.
En efecto: 1 - 1 = 0, 1 - 2 + 1 = 0, 1 - 3 + 3 - 1 = 0, 1 - 4 + 6 - 4 + 1 = 0, 1 - 5 + 10 - 10 + 5 1 = 0 ... Las propiedades que hemos observado en el tringulo se pueden ahora escribir con todo rigor: .
(costados izquierdos y derechos del tringulo).
. ("segunda capa"). .
(simetra respecto al eje vertical del tringulo).
cuando p > n (corresponde a la zona fuera del tringulo).
Y claro, la regla de construccin del tringulo da la relacin fundamental de los coeficientes binomiales: .
Interpretacin en combinatoria
Los coeficientes binomiales son la base misma de la combinatoria. Veamos por qu: Tomemos de nuevo un binomio, por ejemplo (a + b)3, y desarrollmoslo, pero de una manera distinta del prrafo anterior:
luego quitemos las parntesis, pero sin cambiar el orden en los productos, es decir sin aplicar la conmutatividad:
Y agrupemos los trminos que contienen el mismo nmero de a, (y de b):
El primer parntesis contiene todas las palabras constituidas de un b y dos a. En este caso, es fcil ver que hay exactamente tres. En el caso general, para contar las palabras, hay que aplicar la conmutatividad, pues las palabras que contienen el mismo nmero de a y b darn el mismo trmino:
El primer factor 3, que es El segundo factor 3, que es
cuenta las tres palabras mencionadas (aab, aba y baa). cuenta las palabras hechas de dos b y un a (abb, bab y bba).
Obviamente, slo hay una palabra de tres letras constituidas de a solamente, y esto corresponde al monomio 1a, con 1 = ( 0 por ninguna b).
En vez de hablar de palabras formadas con a y b, es equivalente imaginar una hilera de n cajones inicialmente vacos, y p bolas intercambiables que se tienen que repartir, en cada cajn no cabiendo ms de una. Se trata en todos casos de repartir p objetos entre n sitios posibles, o de escoger un grupo de p objetos/sitios entre n objetos/sitios. De ah la apelacin p entre n. Todo lo anterior lleva al teorema:
Hay exactamente
maneras de escoger un conjunto de p elementos entre n elementos.
En matemtica formal, se prefiere hablar de conjuntos:
Existen
subconjuntos de cardinal p en un conjunto de cardinal n.
Este punto de vista permite hallar la frmula para los coeficientes binomiales. En efecto, para elegir el primer elemento, hay n posibilidades, luego para escoger el segundo quedan n-1 posibilidades y as sucesivamente hasta el elemento nmero p, que tiene n-p+1. El orden en el que se ha elegido estos p elementos no importa, se poda haber obtenido el mismo subconjunto de p elementos en otro orden. Hay p! permutaciones posibles de estos p elementos, es decir p! maneras de obtener el mismo conjunto.
Por tanto hay En conclusin:
subconjuntos posibles.
Verifiqumoslo en un ejemplo:
En el tringulo, el valor en la quinta lnea y segunda columna es 10. Para rematar, listemos las palabras de cinco letras formadas de 2 a y 5-2 = 3 b (en el orden alfabtico, o en el orden creciente considerando que a es la cifra 0 y b la cifra 1): aabbb, ababb, abbab, abbba, baabb, babab, babba, bbaab, bbaba, bbbaa. La frmula permite verificar todas las propiedades del prrafo anterior, sin embargo se puede prescindir de los clculos en la mayora de los casos, con tal de manipular los conceptos idneos.
Un subconjunto A de E define una particin de E en dos partes E = A B , con A B = {}= (conjunto vaco). Aqu es el complementario de A en E. Da lo mismo escoger los p elementos de A que los n-p elementos de .
Esto justifica, sin clculo, la simetra . Si p > n, no hay subconjuntos de E con p elementos, porque E contiene slo n, luego Tambin son evidentes las igualdades y porque, en el primer caso,
hay tantas maneras de escoger subconjunto de tamao 1 que de elementos de E, y en el segundo caso, slo existe un conjunto con cero elemento: el conjunto vaco. La regla fundamental tambin tiene explicacin grfica: Prueba: se escoge un elemento e cualquiera de E, que contiene n+1 elementos: E = E' {e}. Luego se consideran los subconjuntos A de E de cardenal p+1. Son de dos tipos: o contienen e, o no. Si e A, entonces falta elegir p elementos de E' para completar A. Hay
posibilidades.
Si e A, entonces falta elegir p+1 elementos de E' para definir A. Hay
posibilidades.
Sumando los dos casos, se obtiene todos las partes de p+1 elementos de E, constituido de n+1 elementos.
Hay por tanto
Un ejemplo:
Aqu va una propiedad aritmtica, sin interpretacin geomtrica: cuando n es primo, los coeficientes binomiales en la lnea n son divisibles por n, excepto los dos bordes de la misma (que valen 1). Escrito formalmente:
Teorema:
Si p es primo entonces p divide a
para k=2,3,...,n-1.
En la figura, los ejemplos estn en verde, y los contraejemplos (cuando n no es primo y p divide n) en amarillo. Prueba: en la fraccin el factor primo
n aparece una vez en el numerador y jams en el denominador. (El denominador es un producto de nmeros entre 1 y n-1). Por tanto la fraccin es divisible por n.
Generalizacin
En vez de considerar las potencias de a + b, se puede mirar las del trinomio a + b + c. (a + b + c)n es una suma de monomios de la forma p, q, r apbqcr, con p, q y r positivos, p + q + r = n, y p, q, r un natural que se tendra que llamar coeficiente trinomial.
Los clculos son similares a los del coeficiente binomial, y dan la expresin siguiente:
Corresponde al nmero de particin en tres de un conjunto de n elementos, en subconjuntos de p, q y r elementos. Un ejemplo:
Estos coeficientes se pueden hallar en la analoga tridimensional del tringulo de Pascal: Se podra llamar la pirmide de Pascal, es tambin infinita, con secciones triangulares, y el valor en cada casilla es la suma de los valores de las tres casillas encima de ella.
Se ha dibujado las primeras secciones a partir de la cumbre. Se observa una invariante por rotacin de 120 grados alrededor de un eje vertical que pasa por el vrtice. El tringulo de Pascal aparece en las tres caras de la pirmide.
Est claro que todo esto se puede generalizar a dimensiones finitas cualquieras, pero sin la posibilidad de hacer dibujos explicativos.
Otra forma de dibujar el tringulo
La ilustracin al comienzo del artculo muestra el tringulo de Tartaglia o Pascal dibujado como un tringulo equiltero. Es posible enderezarlo de tal forma que su dibujo quede como un tringulo rectngulo. De esta forma, a la izquierda queda una columna de nmeros 1. La siguiente columna deja un lugar vaco en la primera fila y sigue con la sucesin de nmeros naturales: 1, 2, 3, 4, ..., n, .... La tercera columna deja dos filas vacas y comienza con la sucesin de los nmeros triangulares: 1, 3, 6, 10, 15, .... Dibujado de esta manera es fcil ver que:
Cada nmero en una columna cualquiera es igual a la suma parcial de los elementos de la columna anterior (a la izquierda) hasta la fila anterior en orden descendente. La tercera columna es la sucesin de los nmeros triangulares; la cuarta, la de los nmeros tetradricos; la quinta, la de los nmeros pentadricos, y as sucesivamente.
Vous aimerez peut-être aussi
- Triángulo de PascalDocument11 pagesTriángulo de PascalRe-ru MartínezPas encore d'évaluation
- Triángulo de PascalDocument10 pagesTriángulo de PascalJhoel ZabalaPas encore d'évaluation
- Triángulo de PascalDocument12 pagesTriángulo de Pascalnena-lettyPas encore d'évaluation
- Triángulo de PascalDocument10 pagesTriángulo de PascalBeto ChavezPas encore d'évaluation
- Triangulo de PascalDocument4 pagesTriangulo de PascalJavier Fajardo BorjaPas encore d'évaluation
- Coeficiente BinomialDocument21 pagesCoeficiente BinomialINGENIEROSPas encore d'évaluation
- Notacion FactorialDocument14 pagesNotacion FactorialStephany Scott60% (5)
- Teorema Del BinomioDocument10 pagesTeorema Del Binomiodiego fernando quispe ariasPas encore d'évaluation
- Resumen Capítulo 0 ÁlgebraDocument3 pagesResumen Capítulo 0 ÁlgebrarsrodrickPas encore d'évaluation
- Conceptos Fundamentales de MatemáticasDocument11 pagesConceptos Fundamentales de MatemáticasPaolaPas encore d'évaluation
- IntroducciónDocument8 pagesIntroduccióncaballero1045Pas encore d'évaluation
- 2.principio de ConteoDocument14 pages2.principio de ConteoPerla VilleAlPas encore d'évaluation
- Coeficiente Binomial e Identidades CombinatoriasDocument35 pagesCoeficiente Binomial e Identidades CombinatoriasZaya SOPas encore d'évaluation
- MatematicaDocument27 pagesMatematicaSariath Azocar100% (1)
- Binomio de NewtonDocument6 pagesBinomio de NewtonEl_kenken_100% (1)
- Apuntes Analisis MatematicoDocument0 pageApuntes Analisis MatematicoDiana Carolina Romero AlavePas encore d'évaluation
- Definición de ArgumentoDocument4 pagesDefinición de ArgumentoYaneri SeverinoPas encore d'évaluation
- El Triángulo de Tartaglia o de Pascal y Su Relación Con El Binomio de NewtonDocument3 pagesEl Triángulo de Tartaglia o de Pascal y Su Relación Con El Binomio de NewtonZaryab AliPas encore d'évaluation
- Los Números EnterosDocument8 pagesLos Números EnterosStacey PetersonPas encore d'évaluation
- Propiedades de La ProbabilidadDocument6 pagesPropiedades de La ProbabilidadLUIS ENRIQUE CAMACHO GRANADOSPas encore d'évaluation
- Teoría de Los ConjuntosDocument22 pagesTeoría de Los ConjuntosVICMA DÍAZPas encore d'évaluation
- RadicalesDocument12 pagesRadicalesInternet PazPas encore d'évaluation
- 4 Suceciones y SeriesDocument10 pages4 Suceciones y SeriesvanessaPas encore d'évaluation
- Cómo Encontrar El Vértice de Una Ecuación CuadráticaDocument17 pagesCómo Encontrar El Vértice de Una Ecuación Cuadráticakelly pedrozaPas encore d'évaluation
- Unidad 1Document23 pagesUnidad 1Oscar Rolando Perez GarciaPas encore d'évaluation
- 4TO. Trabajo de Matematica Elvis Quintero 4to BDocument23 pages4TO. Trabajo de Matematica Elvis Quintero 4to BmerlyPas encore d'évaluation
- 11 MATEMATICAS I Segunda ParteDocument24 pages11 MATEMATICAS I Segunda ParteCarlos DominguezPas encore d'évaluation
- Ternas PitagóricasDocument7 pagesTernas PitagóricasxD_RnGado100% (1)
- 2 ConjuntosDocument20 pages2 Conjuntosagucol12Pas encore d'évaluation
- Numeros ConstructiblesDocument12 pagesNumeros ConstructiblesJeans Mago100% (1)
- Recurso 1Document15 pagesRecurso 1KAREN STEFFANY COLON CARABALLOPas encore d'évaluation
- Conjuntos NuméricosDocument4 pagesConjuntos NuméricosValentina SanchezPas encore d'évaluation
- 3-Cardinalidad (Hernán de La Vega)Document5 pages3-Cardinalidad (Hernán de La Vega)Antoo Zabala MileraPas encore d'évaluation
- Número CombinatorioDocument18 pagesNúmero CombinatorioJRAADESMPas encore d'évaluation
- Teoria de Conjuntos Algebra ModernaDocument17 pagesTeoria de Conjuntos Algebra ModernaCesar A. Escorcia100% (2)
- Número CardinalDocument4 pagesNúmero Cardinalatabeg7Pas encore d'évaluation
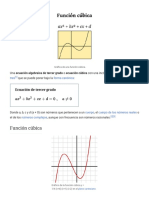
- Ecuación de Tercer Grado - Wikipedia, La Enciclopedia LibreDocument9 pagesEcuación de Tercer Grado - Wikipedia, La Enciclopedia LibreWilliam Dextre DiazPas encore d'évaluation
- Notas CombinatoriaDocument13 pagesNotas CombinatoriadezPas encore d'évaluation
- Cardinal de Una Unión de Conjuntos. Artículo de La Enciclopedia.Document4 pagesCardinal de Una Unión de Conjuntos. Artículo de La Enciclopedia.Alfredo Ayala OrtegaPas encore d'évaluation
- FactorizaciónDocument9 pagesFactorizaciónclarotecniPas encore d'évaluation
- Álgebra - L1 - Enlace Web - Conjuntos Numéricos y Algunas PropiedadesDocument4 pagesÁlgebra - L1 - Enlace Web - Conjuntos Numéricos y Algunas PropiedadesAdalberto Ornelas RenteriaPas encore d'évaluation
- 2010 Matematicas 04 13Document50 pages2010 Matematicas 04 13kudasai_sugoiPas encore d'évaluation
- 20 Raices de EcuacionesDocument12 pages20 Raices de EcuacionesAriz GarciaPas encore d'évaluation
- La Permutación y Combinación de Los Números NaturalesDocument33 pagesLa Permutación y Combinación de Los Números NaturalescristggPas encore d'évaluation
- Algebra I Desarrollo de BinomiosDocument7 pagesAlgebra I Desarrollo de BinomiosRuiz Betanzos EmilioPas encore d'évaluation
- COMBINATORIADocument14 pagesCOMBINATORIAMiguel Christian Infante LópezPas encore d'évaluation
- Guía de Estudio Números RealesDocument7 pagesGuía de Estudio Números RealesPark BæPas encore d'évaluation
- Mono MioDocument13 pagesMono Miosear_motaPas encore d'évaluation
- FactorizaciónDocument10 pagesFactorizaciónwanderley trujilloPas encore d'évaluation
- Evaluar Un PolinomioDocument8 pagesEvaluar Un PolinomioEdgardo Rito DehezaPas encore d'évaluation
- Triángulo de PascalDocument5 pagesTriángulo de PascalMiguel HernándezPas encore d'évaluation
- La Teoría de ConjuntosDocument11 pagesLa Teoría de ConjuntosRafael MatizPas encore d'évaluation
- BINOMIO DE NEWTON TareaDocument2 pagesBINOMIO DE NEWTON TareaHarol Joseph Camacho ChiloPas encore d'évaluation
- FACTORIZACIONDocument7 pagesFACTORIZACIONPaola Daniela Eguez MayorgaPas encore d'évaluation
- Factorizacion 345Document6 pagesFactorizacion 345Nery100% (1)
- Triángulo de Pascal - Wikipedia, La Enciclopedia LibreDocument33 pagesTriángulo de Pascal - Wikipedia, La Enciclopedia Libreguillermo barretoPas encore d'évaluation
- Curso básico de teoría de númerosD'EverandCurso básico de teoría de númerosÉvaluation : 5 sur 5 étoiles5/5 (2)
- Algoritmos: análisis, diseño e implementaciónD'EverandAlgoritmos: análisis, diseño e implementaciónPas encore d'évaluation
- Hoja de Trabajo #25 - AreasDocument7 pagesHoja de Trabajo #25 - AreasBrayan Vasquez FarroPas encore d'évaluation
- Educación General Basica Superior Intercultural BilingueDocument6 pagesEducación General Basica Superior Intercultural BilingueLuis Antonio GuamanPas encore d'évaluation
- 4 - Propiedades de Los ExponentesDocument6 pages4 - Propiedades de Los ExponentesMarìa Briceño OrtegaPas encore d'évaluation
- Portafolio ListoDocument16 pagesPortafolio ListoEduardo VarguezPas encore d'évaluation
- Factorizacion de Binomios y La Formula CuadráticaDocument5 pagesFactorizacion de Binomios y La Formula CuadráticaEnrrique EscobarPas encore d'évaluation
- Aplicación de Procedimientos para La Solución de Una Situación o ProblemaDocument5 pagesAplicación de Procedimientos para La Solución de Una Situación o ProblemaSantiago PatiñoPas encore d'évaluation
- Apolonio de PergeDocument2 pagesApolonio de PergeKarla GuanipaPas encore d'évaluation
- Funciones RealesDocument33 pagesFunciones RealesJonathan Tafur LuckPas encore d'évaluation
- Estándares y Expectativas de Matemáticas 11mo GradoDocument7 pagesEstándares y Expectativas de Matemáticas 11mo GradoTaller Sigma80% (5)
- Planificacion OctavoDocument11 pagesPlanificacion OctavoKatherinne Andrea Sepulveda Sagal100% (1)
- Aritmetica Numeros Con Signo 3Document14 pagesAritmetica Numeros Con Signo 3YulianaKarenPumaFlorezPas encore d'évaluation
- Tarea 2. - Elementos y Ecuaciones de La CircunferenciaDocument8 pagesTarea 2. - Elementos y Ecuaciones de La Circunferenciajavier vega0% (1)
- Sum1p2 Matematicas 2 Semestre 22 ADocument6 pagesSum1p2 Matematicas 2 Semestre 22 AJesus OchoaPas encore d'évaluation
- Tes Completos de Ecuaciones (2) - CompressedDocument87 pagesTes Completos de Ecuaciones (2) - CompressedALDO MAURICIO NARANJO MORAN0% (1)
- Potenciacion y CaracteristicasDocument4 pagesPotenciacion y Caracteristicascrykill3575% (4)
- 12 Funciones RoloDocument4 pages12 Funciones RoloARNY FLORESPas encore d'évaluation
- 163 Ingreso 2012Document45 pages163 Ingreso 2012Mei NikPas encore d'évaluation
- Numeros Reales I PDFDocument10 pagesNumeros Reales I PDFandresPas encore d'évaluation
- M5 - División EnteraDocument2 pagesM5 - División EnteraVeroo CheresPas encore d'évaluation
- Circunferencia Trigonométrica Secante y Cosecante PDFDocument3 pagesCircunferencia Trigonométrica Secante y Cosecante PDFl1m0Pas encore d'évaluation
- Curso 0 - IntegralesDocument60 pagesCurso 0 - Integralesfz fzxcPas encore d'évaluation
- Boletin 2 Geometría Avanzado UniDocument18 pagesBoletin 2 Geometría Avanzado UniCALDERON ROSALES WILLIAM CHARLYPas encore d'évaluation
- 2.1 Criterios de DivisibilidadDocument2 pages2.1 Criterios de Divisibilidadminerva castilloPas encore d'évaluation
- Trabajo de Investigación de MatemáticasDocument19 pagesTrabajo de Investigación de MatemáticasEddy Pavón AlvarezPas encore d'évaluation
- Factorial de Un NúmeroDocument3 pagesFactorial de Un NúmeroJEAN CARLOS MATOS QUIJANDRIAPas encore d'évaluation
- Semana 6Document6 pagesSemana 6danyelly gomezPas encore d'évaluation
- PM Tema 1Document4 pagesPM Tema 1Jovany ArjonaPas encore d'évaluation
- Sesión - Sistema Ecuaciones LInealesDocument19 pagesSesión - Sistema Ecuaciones LInealesFrank Gomez bernillaPas encore d'évaluation
- Ejerc 1erc (Sede)Document6 pagesEjerc 1erc (Sede)Sergio BravoPas encore d'évaluation
- Logaritmos (Cuadernillo) 2022Document5 pagesLogaritmos (Cuadernillo) 2022SanBe ImpresionesPas encore d'évaluation