Académique Documents
Professionnel Documents
Culture Documents
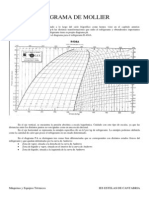
Fasciculo 2
Transféré par
Roger ParraTitre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Fasciculo 2
Transféré par
Roger ParraDroits d'auteur :
Formats disponibles
Fascculos de
Algebra Lineal
Segundo Fascculo:
Algebra Matricial
Neptal Romero
Universidad Centroccidental Lisandro Alvarado
Decanato de Ciencias y Tecnologa
Unidad de Investigaci on en Ciencias Matem aticas
Departamento de Matem aticas
Marzo, 2006
Indice general
2.
Algebra Matricial 3
2.1. Nota Hist orica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2. Matrices: Denici on y Ejemplos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.3. Algunas Matrices Especiales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.3.1. Matrices Triangulares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.3.2. Matrices Diagonales y Escalares. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.3.3. Matrices Simetricas y Antisimetricas. . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.3.4. Matriz Traspuesta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.4. Operaciones con matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.4.1. Estructura vectorial o lineal de M
mn
(K) . . . . . . . . . . . . . . . . . . . . . . . 10
2.4.2. Multiplicaci on de matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.4.3. Matrices Invertibles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.5. Operaciones Elementales por las y Matrices Elementales . . . . . . . . . . . . . . . . . . 22
2.5.1. Denici on, ejemplos y propiedades generales . . . . . . . . . . . . . . . . . . . . . . 22
2.5.2. Forma can onica de Gauss-Jordan . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.5.3. Operaciones Elementales por las y Matrices Invertibles . . . . . . . . . . . . . . . 34
2.6. Ejercicios Propuestos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
2
2
Algebra Matricial
2.1. Nota Hist orica
Las nociones primarias sobre las matrices se dice que datan del siglo II antes de Cristo; sin embargo
existen evidencias rudimentarias del uso de las mismas en el siglo IV antes de Cristo. Tomando en
consideraci on tales evidencias, se sostiene que los comienzos del uso de la herramienta matricial est a ligado
a la resoluci on de problemas que en la actualidad denominamos sistemas de ecuaciones lineales. De hecho,
en la antigua Babilonia se estudiaron problemas que involucraban ecuaciones lineales simult aneas; algunos
de tales problemas eran conservados en tablillas de arcilla
1
. Por ejemplo, una de estas tablillas, la cual
se cree fue construida alrededor de 300 a nos antes de nuestra era, contiene el siguiente problema:
Hay dos terrenos cuya area total es de 1800 yardas cuadradas. Uno produce granos en una proporci on
de
2
3
de una medida por yarda cuadrada mientras el otro lo hace en una proporci on de
1
2
de una medida
por yarda cuadrada. Si la producci on total es 1100 medidas, cu al es el tama no de cada terreno?
No obstante, los chinos estuvieron mucho m as cerca de las matrices que los babilonios; en efecto, en el
libro: Nueve Captulos de Arte Matem atico, escrito durante la Dinasta Han entre los a nos 200 y 100
antes de Cristo, existen ejemplos sobre el uso de tecnicas matriciales para resolver problemas relativos a
sistemas de ecuaciones lineales; por ejemplo, el siguiente problema (traducci on mediante!), similar al de
la tablilla Babil onica, se dice est a en tal libro:
Hay tres tipos de cereales, de los cuales tres fardos del primero, dos del segundo, y uno del tercero
hacen 39 medidas. Dos del primero, tres del segundo y 1 del tercero hacen 34 medidas. Y uno del pri-
mero, dos del segundo y tres del tercero hacen 26 medidas. Cu antas medidas de cereal son contenidas
en un fardo de cada tipo?
A pesar de las antiguas evidencias del empleo de las matrices, y rudimentarias tecnicas para la reso-
luci on de sistemas de ecuaciones lineales, no es sino hasta el siglo XIX cuando se desarrolla la estructura
matem atica del
Algebra de matrices. A este desarrollo contribuy o de forma decisiva el matem atico ingles
Arthur Cayley. En 1858 public o Memorias sobre la teora de matrices en la que introduce la denici on
de matriz, las operaciones de adici on, de multiplicaci on de un n umero real por una matriz y de multipli-
caci on de matrices; adem as del concepto de inversa de una matriz. Cayley sustuvo que obtuvo la idea de
matriz a traves de la noci on de determinante y tambien de la transformaciones geometricas de guras.
2
1
Tras la invasi on del ejercito de USA y sus aliados a Irak en el a no 2003, muchas evidencias culturales, entre ellas antiguas
tablillas de arcilla que contenan los primeros registros escritos de la humanidad, han sido destruidas, o hurtadas. El lector
interesado puede consultar el libro. La destrucci on cultural de Irak. Un testimonio de Postguerra. Fernando B aez. Alfadil
Ediciones/Octaedro - Flor de Viento. (2005)
2
Para acceder, electr onicamente, a informaci on sobre la historia de las matrices, el lector puede consultar las siguientes
direcciones: a) www-history.mcs.st-andrews.ac.uk/history/HistTopics/Matrices and determinants.html
b) palillo.usach.cl/Pamela/historia.htm y c) www.omerique.net/calcumat/matrices1.htm, de donde se ha tomado alguna de
la informaci on suministrada arriba.
3
4 2.
Algebra Matricial
2.2. Matrices: Denici on y Ejemplos.
En lo que sigue, salvo menci on de lo contrario, Kdenotar a indistintamente tanto al cuerpo conmutativo
de los n umeros reales como el de los n umeros complejos; esto es, los conjuntos R y C dotados de las
operaciones usuales de adici on y multiplicaci on con las propiedades ya conocidas.
Denici on 2.1. Dados dos enteros m 1 y n 1. Una matriz de orden mn en K es cualquier arreglo
bidimensional con m las y n columnas, una tal matriz se representa por
A =
_
_
a
11
a
12
a
1n
a
21
a
22
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
a
m2
a
mn
_
_
, (2.1)
los coecientes de A (tambien llamados componentes o entradas de A) son valores cualesquiera en K.
Estas entradas se denotan por a
ij
, con i tomando valores enteros entre 1 y m (que son las las de A);
mientras que j vara en el rango 1, , n, que determina el n umero de columnas de la matriz.
Comentario 2.1. El doble subndice ij determina la posici on que ocupa en el arreglo el coeciente a
ij
;
tal posici on es la intersecci on de la la i con la columna j; entendiendose como las de A los renglones
horizontales del arreglo, y como columnas los renglones verticales. Estos renglones (las y columnas) son
enumerados de forma creciente desde 1 hasta m y de 1 hasta n, respectivamente.
Al conjunto de todas las matrices de orden m n sobre R se denota por M
mn
(R); en cuanto que
M
mn
(C) denota al conjunto de todas las matrices de orden mn sobre C; m as generalmente, M
mn
(K)
denota el conjunto de de todas las matrices de orden mn sobre K, con K = R o K = C.
A lo largo de estas notas emplearemos la notaci on dada en (2.1); sin embargo para efectos pr acti-
cos tambien usaremos la nomenclatura abreviada A = [a
ij
]
mn
, donde a
ij
K es el coeciente de A
ubicado en la la i y columna j de la matriz A. Tambien emplearemos las notaciones que a continua-
ci on describimos. Si denotamos cada la de A = [a
ij
]
mn
por A
(1)
, A
(2)
, , A
(m)
, y cada columna por
A
(1)
, A
(2)
, , A
(n)
, entonces
_
_
A
(1)
A
(2)
.
.
.
A
(m)
_
_
y A = [A
(1)
A
(2)
A
(n)
] denotan la misma matriz A.
Observe que para cada i = 1, , m y j = 1, , n tenemos:
la i : A
(i)
= [a
i1
a
ij
a
in
], y columna j : A
(j)
=
_
_
a
1j
.
.
.
a
ij
.
.
.
a
mj
_
_
Para nalizar este primer comentario, cuando el n umero de las y columnas de una matriz dada
son iguales, diremos que tal matriz es cuadrada . As, para cualquier entero positivo n, denotamos por
M
nn
(K) al conjunto de todas las matrices cuadradas de orden nn con coecientes en K. Adem as, dada
cualquier matriz cuadrada A = [a
ij
]
nn
, al conjunto de los coecientes de A ubicados en las posiciones ii
(a
ii
para cada i = 1, , n) se les conoce como diagonal de A; claramente se observa que los coecientes de
2.2. Matrices: Denici on y Ejemplos. 5
la diagonal de una matriz cuadrada est an dispuestos justamente en la diagonal del arreglo que representa a
la matriz; la siguiente es una matriz cuadrada de orden nn cuyos coecientes son a
ij
con i, j = 1, , n.
A =
_
_
a
11
a
12
a
1n
a
21
a
22
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
a
nn
_
_
, (2.2)
Para la matriz cuadrada de orden 4 4, A =
_
_
2 0 1 3
2 3 1 2
0 0 5 4
0 0 0 2
_
_
, los coecientes encerrados en
crculos determinan la diagonal de A. El vocablo diagonal de una matriz es reservado exclusivamente
para matrices cuadradas.
Denici on 2.2. Dadas dos matrices A = [a
ij
]
mn
y B = [b
ij
]
mn
en M
mn
(K); se dice que son iguales,
se denota por A = B, si, y s olo si, a
ij
= b
ij
para todo i = 1, , m y j = 1, , n. Es decir, A = B si, y
s olo si, son del mismo orden, y coeciente a coeciente ellas son iguales.
Ejemplo 2.1. Los siguientes son ejemplos de distintos tipos de matrices.
1. La matriz nula de orden mn, es aquella matriz de orden mn cuyos coecientes son todos iguales
a cero; se acostumbra denotarla por O
mn
. Por ejemplo:
O
21
=
_
0
0
_
, O
12
=
_
0 0
, O
22
=
_
0 0
0 0
_
, y O
23
=
_
0 0 0
0 0 0
_
son las matrices nulas
de orden 2 1, 1 2, 2 2 y 2 3 respectivamente.
2. La matriz A =
_
_
1 +i 0 1 4
0 2 i 3 i
1 3 2 +i 0
_
_
es de orden 34 con coecientes en C, A M
34
(C).
Note que el coeciente que ocupa la posicion determinada por la la 2 y la columna 3 es i, mientras
que el coeciente ubicado en la la 1 y columna 1 es 1 +i.
3. Una matriz la, o tambien unila, es cualquier matriz que tiene una unica la; es decir, de orden
1 n para alg un entero positivo n. Por ejemplo, la siguiente es una matriz unila en C
A =
_
1 2 i 2 +i 0 1
M
17
(C).
4. Una matriz columna, tambien denominada unicolumna, es cualquier matriz con una unica columna;
es decir, cualquier matriz de orden m 1, para alg un entero positivo m. Por ejemplo la matriz
B =
_
_
2
1
0
4
_
_
es una matriz unicolumna con cuatro las; es decir de orden 4 1 en R; la cual
obviamente tambien puede considerarse como un elemento del conjunto M
41
(C).
5. En el conjunto M
mn
(K) denimos las siguientes m.n matrices: para cada k = 1, , m y cada
= 1, , n, denotamos por E
k
la matriz de M
mn
(K) que tiene en su entrada determinada por
la la k y columna j, el dgito 1, y las restantes entradas son todas iguales a 0. Esto es, E
k
= [e
ij
]
6 2.
Algebra Matricial
en M
mn
(K), donde e
ij
=
_
1; si i = k y j =
0; en otro caso
. Estas matrices se conocen con el nombre de
matrices can onicas de M
mn
(K) .
Por ejemplo en M
22
(K) las matrices can onicas son:
E
11
=
_
1 0
0 0
_
, E
12
=
_
0 1
0 0
_
, E
21
=
_
0 0
1 0
_
y E
22
=
_
0 0
0 1
_
.
6. Para cada entero positivo n, denominamos matriz identidad de orden n, lo cual denotamos por I
n
,
a la matriz cuadrada de orden nn cuyos coecientes de la diagonal son iguales a 1, y los restantes
son todos iguales a 0. En particular tenemos que:
I
1
=
_
1
, I
2
=
_
1 0
0 1
_
, I
3
=
_
_
1 0 0
0 1 0
0 0 1
_
_
y I
4
=
_
_
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
_
_
son las matrices identidad de orden 1 1, 2 2, 3 3 y 4 4, respectivamente.
Note que la matriz identidad I
n
la hemos podido denir por I
n
= [
ij
]
nn
, donde
ij
denota el
denominado delta de Kronecker; esto es,
ij
=
_
1, si i = j
0, si i = j
.
Ejemplo 2.2. Las matrices pueden ser ultilizadas para el almacenamiento de datos.
1. La siguiente matriz suministra informaci on sobre la distancia, medida en kil ometros, entre algunas
de las ciudades de Venezuela:
B
a
r
q
u
i
m
e
t
o
C
a
r
a
c
a
s
M
a
r
a
c
a
i
b
o
M
e
r
i
d
a
Barquimeto
Caracas
Maracaibo
Merida
_
_
0 363 322 421
363 0 706 682
322 706 0 401
421 682 401 0
_
_
.
2. Supongamos que tres productos industriales, Prod. 1, Prod. 2 y Prod. 3, son elaboradors a a partir
de cuatros componentes: A, B, C y D. La siguiente matriz ofrece la informaci on sobre la cantidad
de unidades de cada componente necesaria para la elaboraci on de cada producto.
_
_
A B C D
Prod. 1 2 3 4 5
Prod. 2 1 2 3 0
Prod. 3 2 3 2 1
_
_
.
2.3. Algunas Matrices Especiales
A continuaci on presentaremos algunos subconjuntos se matrices que podramos catalogar de especiales,
y que ser an empleadas m as adelante.
2.3. Algunas Matrices Especiales 7
2.3.1. Matrices Triangulares
Denici on 2.3. Una matriz cuadrada A = [a
ij
]
nn
en M
nn
(K) se denomina triangular superior si
para todo i > j se tiene a
ij
= 0. Al conjunto de matrices triangulares superiores de orden n n sobre K
lo denotamos por TS
n
(K).
Observe que una matriz cuadrada A = [a
ij
]
nn
en M
nn
(K) es triangular superior si, y s olamente si,
todos los elementos que est an por debajo de la diagonal de A son todos iguales a 0.
Ejemplo 2.3.
1. Toda matriz cuadrada nula y la matriz identidad I
n
, para cualquier entero positivo n, son matrices
triangulares superiores.
2. Las siguientes matrices son triangulares superiores:
_
_
0 1 2
0 3 1
0 0 4
_
_
,
_
_
1 0 0
0 3 0
0 0 2
_
_
,
_
_
1 2 3 4
0 1 2 3
0 0 1 2
0 0 0 1
_
_
.
3. Las siguientes matrices no son triangulares superiores:
_
_
0 1 2
0 3 1
0 1 4
_
_
,
_
_
1 0 0
0 3 0
1 0 2
_
_
,
_
_
1 2 3 4
0 1 2 3
1 0 1 2
1 0 0 1
_
_
.
Denici on 2.4. Una matriz cuadrada A = [a
ij
]
nn
en M
nn
(K) se denomina triangular inferior si para
todo i < j se tiene a
ij
= 0. Al conjunto de matrices triangulares inferiores de orden n n sobre K lo
denotamos por TI
n
(K).
Como antes, esta denici on implica que A = [a
ij
]
nn
en M
nn
(K) es triangular inferior si, y s olo si,
todos los elementos que est an por encima de la diagonal de A son todos iguales a 0.
Ejemplo 2.4.
1. La matriz nula O
n
y la matriz identidad I
n
son triangulares inferiores cualquiera que sea el entero
positivo n.
2. Las siguientes matrices son triangulares inferiores:
_
_
0 0 0
1 0 0
1 2 0
_
_
,
_
_
1 0 0
0 3 0
0 0 2
_
_
,
_
_
1 0 0 0
1 2 0 0
1 2 3 0
1 2 3 4
_
_
.
3. Las siguientes matrices no son triangulares inferiores:
_
_
0 1 0
1 0 0
2 1 0
_
_
,
_
_
1 0 1
0 3 0
1 0 2
_
_
,
_
_
1 2 3 4
0 1 2 3
1 0 1 2
1 0 0 1
_
_
.
La forma general de las matrices triangulares superiores e inferiores de orden n n son, respectiva-
mente:
_
_
a
11
a
12
a
1n1
a
1n
a
22
a
2n1
a
2n
.
.
.
.
.
.
.
.
.
O a
n1n1
a
n1n
a
nn
_
_
y
_
_
a
11
a
21
a
22
O
.
.
.
.
.
.
.
.
.
a
n11
a
n12
a
n1n1
a
n1
a
n2
a
nn1
a
nn
_
_
,
8 2.
Algebra Matricial
entendiendose que el smbolo Osignica que todos los coecientes por debajo (resp. por encima) de la
diagonal son iguales a 0.
2.3.2. Matrices Diagonales y Escalares.
Denici on 2.5. Una matriz cuadrada A = [a
ij
]
nn
en M
nn
(K) se denomina matriz diagonal si a
ij
= 0
para todo i = j. Al conjunto de matrices diagonales de orden n n sobre K lo denotamos por D
n
(K).
Claramente toda matriz diagonal es al mismo tiempo triangular superior e inferior, pues todos los
coecientes que no est an en la diagonal son iguales a 0. De hecho, se demuestra de manera muy simple
que D
n
(K) = TS
n
(K) TI
n
(K); dejamos los detalles al lector.
Denici on 2.6. Una matriz cuadrada A = [a
ij
]
nn
en M
nn
(K) se denomina matriz escalar si es
diagonal y existe un escalar K tal que a
ii
= para todo i = 1, , n. Al conjunto de matrices
escalares de orden n n sobre K se denota por E
n
(K).
De esta deniciones sigue que las matrices diagonales y escalares de orden n n en K son, respecti-
vamente, de la forma:
_
_
a
1
a
2
O
.
.
.
O a
n1
a
n
_
_
y
_
O
.
.
.
O
_
;
en ocasiones a la matriz escalar de orden nn que tiene en su diagonal al escalar se le denota por I
n
.
Ejemplo 2.5. Las siguientes matrices son diagonales: [1],
_
2 0
0 3
_
,
_
_
1 0 0
0 1 0
0 0 5
_
_
, para todo n 1 la
matriz identidad I
n
, toda matriz cuadrada nula, toda matriz escalar (E
n
(K) D
n
(K)).
Las matrices escalares son muy simples: son las aquellas matrices diagonales que en su diagonal tienen
el mismo valor. Obviamente existen matrices diagonales que no son escalares.
2.3.3. Matrices Simetricas y Antisimetricas.
Denici on 2.7. Una matriz cuadrada A = [a
ij
]
nn
en M
nn
(K) se denomina matriz simetrica si para
todo i, j = 1, , n con i = j se cumple a
ij
= a
ji
. Al conjunto de matrices simetricas de orden n n
sobre K se denota por S
n
(K).
Denici on 2.8. Una matriz cuadrada A = [a
ij
]
nn
en M
nn
(K) se denomina matriz antisimetrica si
para todo i, j = 1, , n se cumple a
ij
= a
ji
. Al conjunto de matrices antisimetricas de orden n n
sobre K se denota por AS
n
(K).
Ejemplo 2.6.
1. Las siguientes son matrices simetricas:
a) Todas las matrices diagonales, entre ellas, por supuesto, las escalares y en particular la iden-
tidad de orden n y la matriz nula de orden n n para cualquier entero positivo n.
2.3. Algunas Matrices Especiales 9
b)
_
1 0
0 1
_
;
_
1 2
2 1
_
;
_
_
1 2 0
2 3 4
0 4 0
_
_
y
_
_
2 1 2 1
1 0 3 2
2 3 1 4
1 2 4 1
_
_
.
2. Las siguientes son matrices antisimetricas:
a) La matriz nula de orden n n para cualquier entero positivo n.
b)
_
0 1
1 0
_
;
_
0
3 0
_
;
_
_
0 2 0
2 0 4
0 4 0
_
_
y
_
_
0 1 2 1
1 0 3 2
2 3 0 4
1 2 4 0
_
_
.
3. Las siguientes no son matrices simetricas:
_
1 0
2 1
_
;
_
1 2
2 1
_
;
_
_
1 2 0
2 3 4
0 4 0
_
_
y
_
_
2 1 2 0
1 0 3 2
2 3 1 4
1 2 4 1
_
_
(por que?)
4. Las siguientes no son matrices antisimetricas:
_
0 1
1 0
_
;
_
0
2 0
_
;
_
_
0 2 0
2 1 4
0 4 0
_
_
y
_
_
0 1 2 1
1 0 3 2
2 3 1 4
1 2 4 0
_
_
(por que?)
Comentario 2.2. De las propias deniciones de matrices simetricas y antisimetricas se desprenden las
siguientes armaciones, sus vericaciones se dejan al lector:
1. Dada cualquier matriz simetrica A = [a
ij
]
nn
S
n
(K), para cada i = 1, , n, al considerar la
la y columna i de A como puntos en K
n
, se tiene que estos son iguales: la i de A es igual a la
columna i de A.
2. Dada cualquier matriz antisimetrica A = [a
ij
]
nn
AS
n
(K), para todo i = 1, , n, al considerar
la la y columna i de A como puntos en K
n
, se tiene que estos puntos son uno el negativo del otro;
en particular, los coecientes que est an ubicados en la diagonal de A son todos iguales a 0.
3. La unica matriz de orden n n, cualquiera sea el entero n 1, que es al mismo tiempo simetrica
y antisimetrica es la matriiz nula de orden n n.
4. la forma general de las matrices simetricas y antisimetricas de orden n n es, respectivamente,
como sigue:
_
_
a
11
a
12
a
1n
a
12
a
22
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
1n
a
2n
a
nn
_
_
y
_
_
0 a
12
a
1n
a
12
0 a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
1n
a
2n
0
_
_
.
10 2.
Algebra Matricial
2.3.4. Matriz Traspuesta
Denici on 2.9. Dada cualquier matriz A = [a
ij
]
mn
en M
mn
(K), se dene la matriz traspuesta de
A, denotada por A
t
, como la matriz A
t
= [b
k
]
nm
en M
nm
(K) tal que, para cada k = 1, , n y
= 1, , m, se cumple b
k
= a
k
.
A diferencia de las anteriores matrices especiales que hemos introducido, este concepto no est a restricto
exclusivamente a matrices cuadradas; de hecho, y como podr a observarse de la denici on, si una matriz A
tiene m as y n columnas, entonces su traspuesta A
t
tiene n las y m columnas; es decir, se intercambian
el n umero de las y columnas; adem as, para cada i = 1, , m la la i de A es justamente la columna i
de A
t
. Podemos decir entonces que trasponer una matriz signica intercambiar las por columnas.
Ejemplo 2.7. Dada la matriz A =
_
_
1 0 1
2 2 1
3 2 0
0 4 5
_
_
, sigue que A
t
=
_
_
1 2 3 0
0 2 2 4
1 1 0 5
_
_
. En cuanto
que si B =
_
1 2 0 3 4
y C =
_
_
2 0 1
0 1 2
1 2 0
_
_
, entonces B
t
=
_
_
1
2
0
3
4
_
_
y C
t
= C.
Proposici on 2.1. Cualquiera sea la matriz A M
mn
(K) se tiene:
1. (A
t
)
t
= A.
2. A = A
t
si, y s olo si, A es simetrica.
Demostraci on: Supongamos que A = [a
ij
]
mn
y A
t
= [b
k
]
nm
M
nm
(K). Demostraremos la segun-
da parte, la primera queda para el lector.
(=) Si A = A
t
, entonces n = m, adem as, para cada i, j = 1, , m se tiene a
ij
= b
ij
; pero por la
denici on de A
t
sigue que b
ij
= a
ji
, con lo cual la matriz A es simetrica, pues es cuadrada y para cada
i, j = 1, , m se tiene a
ij
= a
ji
.
(=) Recprocamente, supongamos que A es una matriz simetrica. Entonces A es cuadrada (m = n) y
para cada i, j = 1, , m se tiene a
ij
= a
ji
. Si hacemos A
t
= [b
k
]
mm
M
mm
(K), sigue que b
k
= a
k
,
pero por ser A simetrica concluimos que b
k
= a
k
para todo k, = 1, , m; de esta forma, A = A
t
.
2.4. Operaciones con matrices
Ahora nos proponemos introducir tres tipos de operaciones con matrices: las dos primeras (una adici on
y una multiplicaci on de un escalar por una matriz) dotar an al conjunto M
mn
(K) de una misma estructura
algebraica conocida como espacio vectorial, a veces llamada estructura lineal. La tercera operaci on es una
multiplicaci on entre matrices, la cual, junto a las anteriores operaciones, dotar a al conjunto de las matrices
cuadradas de una estructura algebriaca conocida como algebra.
2.4.1. Estructura vectorial o lineal de M
mn
(K)
Denici on 2.10. Llamaremos adici on usual de matrices, o simplemente adici on de matrices, a la ope-
raci on entre matrices del mismo orden con coecientes en K, denotada por el smbolo +, tal que para
2.4. Operaciones con matrices 11
cada par de matrices A, B M
mn
(K) de la siguiente manera:
si A =
_
_
a
11
a
12
a
1n
a
21
a
22
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
a
m2
a
mn
_
_
y B =
_
_
b
11
b
12
b
1n
b
21
b
22
b
2n
.
.
.
.
.
.
.
.
.
.
.
.
b
m1
b
m2
b
mn
_
_
, entonces
A+B =
_
_
a
11
+b
11
a
12
+b
12
a
1n
+b
1n
a
21
+b
21
a
22
+b
22
a
2n
+b
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
+b
m1
a
m2
+b
m2
a
mn
+b
mn
_
_
. (2.3)
Abreviadamente: si A = [a
ij
]
mn
, B = [b
ij
]
mn
M
mn
(K), entonces A + B = [c
ij
]
mn
M
mn
(K) y
para cada i = 1, , m y j = 1, , n se cumple c
ij
= a
ij
+ b
ij
. A la matriz A + B se le conoce con el
nombre de suma de A m as B.
Denici on 2.11. Llamaremos multiplicaci on usual de escalares por matrices, a la operaci on que asocia
a cada escalar K y a cada matriz A =
_
_
a
11
a
12
a
1n
a
21
a
22
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
a
m2
a
mn
_
_
M
mn
(K), otra matriz de
M
mn
(K), que se denota por A, se conoce como producto de por A y se dene por:
A =
_
_
a
11
a
12
a
1n
a
21
a
22
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
a
m2
a
mn
_
_
. (2.4)
De forma abreviada se escribe A = [c
ij
]
mn
, donde c
ij
= a
ij
, para cada i = 1, , m y j = 1, , n,
siempre que K y A = [a
ij
]
mn
M
mn
(K).
Comentario 2.3. Note que las operaciones que acabamos de denir son muy simples, para sumar dos
matrices: ambas deben tener el mismo orden y sus coecientes estar en K, y la entrada ubicada en la la
i con la columna j de la matriz suma, es igual a la suma de los correspondientes n umeros ubicados en la
misma posici on dentro de las matrices que estamos sumando. En cuanto al producto de un escalar por
una matriz, basta multiplicar el escalar dado por cada una de los valores ubicados en cada una de las
entradas de la matriz dada.
Ejemplo 2.8.
1. Dadas A =
_
_
1 +i 1 0
2 i 2
0 3 2 i
1 2 1
_
_
, B =
_
_
1 i 2 1
2 i 1
1 1 i
0 0 1
_
_
y = 2, tenemos:
A+B =
_
_
(1 +i) + (1 i) 1 + 2 0 + 1
2 + (2) i +i 2 + 1
0 + 1 3 + 1 2 i +i
1 + 0 2 + 0 1 + 1
_
_
=
_
_
2 1 1
0 0 3
1 2 2
1 2 2
_
_
y B =
_
_
2 2i 4 2
4 2i 2
2 2 2i
0 0 2
_
_
.
12 2.
Algebra Matricial
2. Sea O = [o
ij
]
mn
la matriz nula de orden m n. Cualquiera sea A = [a
ij
]
mn
M
mn
(K) se
cumple A+O = A. En efecto, si hacemos A+O = [c
ij
]
mn
, entonces c
ij
= a
ij
+o
ij
= a
ij
+0 = a
ij
para cada i = 1, , m y j = 1, , n. Sigue por tanto de la denici on 2.10 que A+O = A.
3. Dada la matriz A = [a
ij
]
mn
M
mn
(K), sea B = [b
ij
]
mn
M
mn
(K) tal que b
ij
= a
ij
para
todo i = 1, , m y j = 1, , n. Entonces tenemos
A+B = [a
ij
]
mn
+ [b
ij
]
mn
= [a
ij
+b
ij
]
mn
= [a
ij
+ (a
ij
)]
mn
= [o
ij
]
mn
, donde o
ij
= 0, i = 1, , m, j = 1, n.
De esta forma A + B = O. Puede demostrarse, de hecho ver pr oximo teorema, que B es la unica
matriz en M
mn
(K) que tiene esta propiedad.
4. La suma de dos matrices tambien puede ser empleada para almacenar informaci on. Consideremos
una empresa que tiene dos f abricas ubicadas en diferentes ciudades: digamos ciudad A y ciudad
B. En ambas f abricas se producen los mismos 3 productos: P1, P2 y P3. El costo de producci on
de una unidad de cada producto en cada f abrica depende de los costos de insumos y del pago al
personal de cada f abrica. Las matrices A y B expresan los costos de producci on, en bolvares, de
cada producto en las f abricas ubicadas en las ciudades A y B respectivamente:
A =
_
_
Insumos Personal
P1 25 300
P2 15 250
P3 22 310
_
_
y B =
_
_
Insumos Personal
P1 26 310
P2 20 280
P3 19 294
_
_
;
por ejemplo, la la 2 de la matriz A dice que el costo de producci on de una unidad del P2 en la
f abrica de la ciudad A esta discriminado de la siguiente forma: 15 bolvares en insumos y 250 en
pago al personal.
De esta forma la matriz C = A + B =
_
_
Insumo Personal
Prod. 1 51 610
Prod. 2 35 530
Prod. 3 41 604
_
_
contiene la informaci on
global de los costos de producci on de los tres productos de la empresa. Por ejemplo, la la 2
contiene la informaci on global del costo de producci on de una unidad del producto P2 en ambas
f abricas, y discriminado en insumos y pagos al personal.
Teorema 2.1 (Estructura Lineal de M
mn
(K)). Cualesquiera sean las matrices A, B y C en
M
mn
(K) y los escalares , K siempre se satisfacen las siguientes propiedades:
[A1] A+B = B +A. (Conmutatividad)
[A2] (A+B) +C = A+ (B +C). (Asociatividad)
[A3] Existe una unica matriz O
en M
mn
(K) tal que para cada A M
mn
(K) vale O
+ A = A; de
hecho O
es la matriz nula de orden mn. (Elemento neutro)
[A4] Para cada A en M
mn
(K) existe una unica matriz A
M
mn
(K) tal que A + A
= O; de hecho
A
= [b
ij
]
mn
con b
ij
= a
ij
para todo i = 1, , m y cada j = 1, , n. A
se conoce por matriz
opuesta y se denota por A. (Elemento simetrico)
[M1] (A+B) = A+ B. (Distributividad)
2.4. Operaciones con matrices 13
[M2] ( +)A = A+A. (Distributividad)
[M3] ()A = ( A) = (A).
[M4] 1 A = A.
Demostraci on: Mostraremos algunos de los enunciados del teorema, el resto se deja como un ejercicio
para el lector.
[A2] Sean A = [a
ij
]
mn
, B = [b
ij
]
mn
y C = [c
ij
]
mn
matrices en M
mn
(K). Entonces:
(A+B) +C = ([a
ij
]
mn
+ [b
ij
]
mn
) + [c
ij
]
mn
= [a
ij
+ b
ij
]
mn
+ [c
ij
]
mn
= [(a
ij
+b
ij
) +c
ij
]
mn
= [a
ij
+ (b
ij
+c
ij
)]
mn
(por que?)
= [a
ij
]
mn
+ [b
ij
+c
ij
]
mn
= A+ (B +C).
[A4] En el anterior ejemplo mostramos que para toda matriz A = [a
ij
]
mn
, la matriz B = [b
ij
]
mn
con
b
ij
= a
ij
para todo i = 1, , m y j = 1, , n, hace que A+B sea la matriz nula. Veamos ahora que
esta es la unica con esa propiedad. Supongamos que C = [c
ij
]
mn
es tal que A + C = O; es decir, para
cada i = 1, , m y j = 1, , n se satisface a
ij
+ c
ij
= 0. Dado que tanto a
ij
como c
ij
son n umeros
en K y a
ij
+ c
ij
= 0, entonces c
ij
= a
ij
para cada i = 1, , m y j = 1, , n. Lo cual demuestra la
unicidad de la matriz que sumada a A resulta la matriz nula. En adelante a esta matriz la denotaremos
por A.
Proposici on 2.2 (Propiedades adicionales). Cualesquiera sean las matrices A, B, C en M
mn
(K),
siempre se cumplen las siguientes propiedades:
1. A+B = A+C, entonces B = C (Ley de Cancelaci on).
2. A = O si, y s olo si, = 0 o A es la matriz nula.
3. Si A
denota la matriz opuesta de A M
mn
(K), entonces A
= (1)A.
4. (A+B)
t
= A
t
+B
t
y (A)
t
= A
t
, para todo K.
5. Cualesquiera sean los enteros k, 2, los escalares
1
, ,
k
K y las matrices A
1
, , A
en
M
mn
(K), siempre se satisfacen:
a) (A
1
+ +A
k
) = A
1
+ +A
k
; abreviadamente se escribe:
_
k
i=1
A
i
_
=
k
i=1
A
i
.
b) (
1
+ +
k
)A =
1
A+ +
k
A; abreviadamente:
_
k
i=1
i
_
A =
k
i=1
i
A.
Demostraci on: Mostraremos algunas de las propiedades enunciadas, las dem as se dejan como ejercicio
para el lector.
2. Dados K y A = [a
ij
]
mn
M
mn
(K) tenemos
A = O [a
ij
]
mn
= [o
ij
]
mn
, donde o
ij
= 0 para todo i = 1, m, j = 1, , n
[a
ij
]
mn
= [o
ij
]
mn
, donde o
ij
= 0 para todo i = 1, m, j = 1, , n
a
ij
= 0 para todo i = 1, m, j = 1, , n
= 0 o a
ij
= 0 para todo i = 1, m, j = 1, , n. (por que?)
14 2.
Algebra Matricial
Esto claramente demuestra la segunda parte del teorema.
5b). Usaremos inducci on matem atica sobre el entero k 2. Supongamos que k = 2; veriquemos que
(
1
+
2
)A =
1
A+
2
A. En efecto, si hacemos A = [a
ij
]
mn
M
mn
(K), entonces
(
1
+
2
)A = (
1
+
2
)[a
ij
]
mn
= [(
1
+
2
)a
ij
]
mn
= [
1
a
ij
+
2
a
ij
]
mn
= [
1
a
ij
]
mn
+ [
2
a
ij
]
mn
(por que?)
=
1
[a
ij
]
mn
+
2
[a
ij
]
mn
=
1
A+
2
B.
Supongamos ahora como cierto (hip otesis inductiva) que para todo entero k entre 2 y 1 se cumple
(
1
+ +
k
)A =
1
A+ +
k
A.
Mostraremos entonces que la misma identidad vale cuando k = . En efecto:
(
1
+ +
1
+
)A = ((
1
+ +
1
) +
)A
= (
1
+ +
1
)A+
A (por que?)
= (
1
A+ +
1
A) +
A (por que?)
=
1
A+ +
1
A+
A.
La propiedad 5a) se muestra similarmente.
En vista que la suma de matrices del mismo orden y el producto de un escalar por una matriz producen
matrices del mismo orden (son operaciones cerradas!), podemos efectuar cualquier cantidad nita de tales
operaciones; esto tiene un signicado muy especial en el
Algebra Lineal, a continuaci on formalizamos esta
noci on.
Denici on 2.12. Dado un n umero nito de matrices del mismo orden: A
1
, A
2
, , A
en M
mn
(K),
decimos que A M
mn
(K) es combinaci on lineal de A
1
, A
2
, , A
, si existen escalares
1
,
2
, ,
en K, tales que A se expresa como:
A =
1
A
1
+
2
A
2
+ +
.
Al conjunto de todas las combinaciones lineales de las matrices A
1
, A
2
, , A
en M
mn
(K) lo denotamos
por CL({A
1
, A
2
, , A
}); esto es,
A CL({A
1
, A
2
, , A
})
1
, ,
K tales que A =
1
A
1
+
2
A
2
+ +
.
Ejemplo 2.9.
1. La matriz nula de orden m n es combinaci on lineal de cualquier n umero nito de matrices
A
1
, , A
en M
mn
(K). Esto sigue del hecho que O
mn
= 0A
1
+ + 0A
k
; recuerde que
0A = O
mn
. En particular esto implica que CL({A
1
, A
2
, , A
}) es siempre un conjunto no vaco,
al menos contiene a la matriz nula.
2. A =
_
2 1 2 2
5 0 6 1
_
es combinaci on lineal de A
1
=
_
1 0 2 1
3 1 4 0
_
y A
2
=
_
0 1 2 0
1 2 2 1
_
, pues
una simple cuenta muestra que A = 2A
1
+ (1)A
2
.
3. Cualquier matriz A =
_
a b
c d
_
es combinaci on lineal de las matrices can onicas E
11
=
_
1 0
0 0
_
,
E
12
=
_
0 1
0 0
_
, E
21
=
_
0 0
1 0
_
y E
22
=
_
0 0
0 1
_
; basta chequear que A = aE
11
+bE
12
+cE
21
+dE
22
.
2.4. Operaciones con matrices 15
4. El ejemplo anterior se generaliza muy f acilmente; es decir, cualquier matriz A = [a
ij
]
mn
M
mn
(K) es combinaci on lineal de las matrices can onicas E
k
de M
mn
(K). Recordemos que
E
k
M
mn
(K) es la matriz de orden mn que tiene en la entrada de la la k y columna al dgi-
to 1, y las restantes entradas son todas iguales a 0. Luego es simple vericar que A =
m
k=1
n
=1
a
k
E
k
;
as que CL({E
11
, E
12
, , E
mn
}) = M
mn
(K).
Comentario 2.4. El problema de decidir si una matriz A es combinaci on lineal de un conjunto nito de
matrices A
1
, , A
es un problema que conduce a resolver simult aneamente un determinado conjunto
nito de cierto tipo de ecuaciones, las cuales ser an estudiadas m as adelante.
2.4.2. Multiplicaci on de matrices
Pasaremos ahora a introducir una operaci on que no necesariamente est a denida para cualquier par
de matrices con entradas en el cuerpo K.
Comenzemos considerando dos matrices, ambas con entradas en K: una de ellas es una matriz unico-
lumna A =
_
a
1
a
2
a
n
y la otra es unila, digamos B =
_
_
b
1
b
2
b
n
_
_
. Se dene el producto de A por
B, lo que denotamos como AB, a la matriz de orden 1 1 cuya unica entrada es
a
1
b
1
+a
2
b
2
+ +a
n
b
n
=
n
j=1
a
j
b
j
; (2.5)
esto es, AB = [c]
11
, donde c =
n
j=1
a
j
b
j
. Claramente esta matriz de orden 1 1 se identica con el
escalar c K; de manera que podemos identicar a AB como un escalar, siempre que A M
1n
(K) y
B M
n1
(K) cualquiera sea el entero positivo n.
Denici on 2.13. Dadas dos matrices A = [a
ik
]
mp
M
mp
(K) y B = [b
kj
]
pn
M
pn
(K). Si
A
(1)
, , A
(m)
son las las de A y B
(1)
, , B
(n)
son las columnas de B, se dene la matriz produc-
to de A por B como la matriz AB = [c
ij
]
mn
(K) M
mn
(K) tal que, para cada i = 1, , m y todo
j = 1, , n se tiene
c
ij
= a
i1
b
1j
+a
i2
b
2j
+ +a
in
b
nj
=
n
k=1
a
ik
b
kj
. (2.6)
Esquem aticamente
AB = [c
ij
]
mn
=
_
_
.
.
.
a
i1
a
i2
a
ip
.
.
.
_
_
_
_
b
1j
b
2j
b
pj
_
_
=
_
_
.
.
.
c
ij
.
.
.
_
_
Comentario 2.5. Observe que la entrada de la la i con la columna j de la matriz producto AB, c
ij
en
(2.6), se obtiene justamente mediante el producto de la matriz unila A
(i)
y la matriz unicolumna B
(j)
;
es decir, c
ij
= A
(i)
B
(j)
para cada i = 1, , m y cada j = 1, , n; ver (2.5).
16 2.
Algebra Matricial
Es importante se nalar que el producto de una matriz A por una matriz B no siempre est a denida; la
matriz producto AB est a denida si, y s olo si, el n umero de columnas de la matriz A es igual al n umero
de las de la matriz B. En particular matrices cuadradas del mismo orden siempre se pueden multiplicar,
y su producto es igualemente una matriz cuadrada del mismo orden.
Ejemplo 2.10.
1. Consideremos las matrices A =
_
_
1 0
2 1
3 1
_
_
y B =
_
2 1 0 2
3 0 1 1
_
. Dado que A es de orden
32 y B de orden 24, entonces tiene sentido el producto AB, pero no el producto BA puesto que
el n umero de columnas de B no es igual al n umero de las de A. Procedamos entonces a calcular
la matriz producto AB. Observe que la matriz AB es, seg un la denici on anterior, de orden 3 4;
esto es, AB =
_
_
c
11
c
12
c
13
c
14
c
21
c
22
c
23
c
24
c
31
c
32
c
33
c
34
_
_
, donde c
ij
= A
(i)
B
(j)
para todo i = 1, 2, 3 y j = 1, 2, 3, 4. As
AB =
_
_
1 0
2 1
3 1
_
_
_
2 1 0 2
3 0 1 1
_
=
_
_
(1)2 + 0 3 (1)1 + 0 0 (1)0 + 0(1) (1)(2) + 0(1)
2 2 + 1 3 2 1 + 1 0 2 0 + 1(1) 2(2) + 1(1)
(3)2 + 1 3 (3)1 + 1 0 (3)0 + 1(1) (3)(2) + 1(1)
_
_
=
_
_
2 1 0 2
7 2 1 5
3 3 1 5
_
_
.
Note adem as que AA ni BB tienen sentido por la misma raz on que BA carece del mismo.
2. Ahora consideremos las matrices A =
_
i 1 i
2 0
_
y B =
_
1 0
2 +i 1
_
. Dado que ambas son
matrices cuadradas del mismo orden, tienen sentido las matrices AA, AB, BA y BB. Calculemos
las matrices producto: AA, BB, AB y BA.
AA =
_
i 1 i
2 0
_ _
i 1 i
2 0
_
=
_
i i + (1 i)2 i(1 i) + (1 i)0
2 i + 0 2 2(1 i) + 0 0
_
=
_
1 2i 1 +i
2i 2 2i
_
;
BB =
_
1 0
2 +i 1
_ _
1 0
2 +i 1
_
=
_
1 1 + 0(2 +i) 1 0 + 0(1)
(2 +i)1 + (1)(2 +i) (2 +i)0 + (1)(1)
_
=
_
1 0
0 1
_
;
AB =
_
i 1 i
2 0
_ _
1 0
2 +i 1
_
=
_
i 1 + (1 i)(2 +i) i 0 + (1 i)(1)
2 1 + 0(2 +i) 2 0 + 0(1)
_
=
_
3 1 +i
2 0
_
;
BA =
_
1 0
2 +i 1
_ _
i 1 i
2 0
_
=
_
1 i + 0 2 1(1 i) + 0 0
(2 +i)i + (1)2 (2 +i)(1 i)
_
=
_
i 1 i
3 + 2i 3 i
_
.
Note que AB = BA, esto dice que la multiplicaci on de matrices, a pesar de estar denidas AB y
BA, no es una operaci on conmutativa.
2.4. Operaciones con matrices 17
3. Consideremos cualquier matriz A M
mn
(K), digamos A =
_
_
a
11
a
12
a
1n
a
21
a
22
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
a
m2
a
mn
_
_
. Dado que
_
0 0 0
_
a
1j
a
2j
.
.
.
a
mj
_
_
= 0; y
_
a
i1
a
i2
a
im
_
0
0
.
.
.
0
_
_
= 0,
se deduce por tanto que si O
pm
y O
n
son las matrices nulas de orden p m y n , entonces
O
pm
A = O
pn
y AO
n
= O
m
, (2.7)
esto es, al multiplicar la matriz nula (por la izquierda o la derecha) por cualquier matriz (siempre
que tenga sentido hacer esta multiplicaci on) el resultado el nuevamente una matriz nula.
Por otra parte, si E
i
(1 i m) es la matriz unila con m columnas tal que son entradas son
iguales a 0, excepto la entrada i-esima que es 1, entonces
E
i
A =
_
0 0 1 0 0
_
a
11
a
12
a
1n
a
21
a
22
a
2n
. . . . . . . . . . . . . . . . . . . . .
a
m1
a
m2
a
mn
_
_
=
_
a
i1
a
i2
a
in
; (2.8)
mientras que si F
j
(1 j j) es la matriz unicolumna con n las tal que son entradas son iguales
a 0, excepto la entrada j-esima que es 1, entonces
AF
j
=
_
_
a
11
a
12
a
1n
a
21
a
22
a
2n
. . . . . . . . . . . . . . . . . . . . .
a
m1
a
m2
a
mn
_
_
_
_
0
.
.
.
0
1
0
.
.
.
0
_
_
=
_
_
a
1j
a
2j
.
.
.
a
mj
_
_
. (2.9)
Claramente de (2.8) y (2.9) se deduce de forma inmediata que si I
m
e I
n
son las matrices identidades
de orden mm y n n respectivamente, entonces I
m
A = A y AI
n
= A.
4. Al igual que la matriz suma, la matriz producto permite almacenar e interpretar cierta informaci on.
Supongamos que un determinado conglomerado de personas: adultos y j ovenes, es clasicado por
sexo, y tales datos se almacenan en el arreglo A =
_
J ovenes Adultos
Masculino 220 98
Femenino 234 105
_
. Por otra
parte, los datos sobre el consumo mensual de carnes, vegetales y frutas, medidos en Kg, de cada
joven y cada adulto se muestran mediante la matriz B =
_
Carnes Vegetales Frutas
J ovenes 4 3 6
Adultos 3 6 8
_
.
18 2.
Algebra Matricial
Luego la matriz producto AB =
_
Carnes Vegetales Frutas
Masculino 1174 1248 2104
Femenino 1251 1332 2244
_
representa la cantidad
de kilogramos de alimentos (carnes, vegetales y frutas) que consume la poblaci on masculina y
femenina de dicho conglomerado; as por ejemplo, el valor 1248 de la la 1 y segunda columna de
AB dice que la poblaci on masculina consume al mes 1248 kilogramos de vegetales.
Teorema 2.2. La multiplicaci on de matrices satisface las siguientes propiedades:
1. Para toda A M
mn
(K) vale: AO
n
= O
m
y O
pm
A = O
pn
, donde O
ks
es la matriz nula
de orden k s cualesquiera sean los enteros positivos k y s.
2. Para toda A M
mn
(K) vale: I
m
A = A y AI
n
= A, siendo que I
k
es la matriz identidad de orden
k k para todo entero positivo k.
3. Cualesquiera sean las matrices A M
mn
(K), B M
np
(K) y C M
p
(K) siempre se cumple
la propiedad asociativa: (AB)C = A(BC).
4. Para todas las matrices A M
mn
(K) y B, C M
np
(K) siempre se cumple la propiedad distri-
butiva: A(B +C) = AB +AC.
5. Para todas las matrices A, B M
mn
(K) y C M
np
(K) siempre se cumple la propiedad distri-
butiva: (A+B)C = AC +BC.
6. Para todo escalar K y A, B M
mn
(K): (AB) = (A)B = A(B).
7. Para todas las matrices A M
mn
(K) y B M
np
(K): (AB)
t
= B
t
A
t
.
Demostraci on: En el ejemplo anterior mostramos las dos primeras propiedades, ahora mostraremos la
tercera septima, las restantes quedan como ejercicio para el lector.
3. Sean A = [a
ij
]
mn
, B = [b
ij
]
np
y C = [c
ij
]
p
, todas con coecientes en K. Dado que el n umero
de columnas de A y de las de B son iguales tiene sentido la matriz producto AB, la cual es de orden
m p. De igual forma tienen sentido las matrices BC, que es de orden n ; por tanto tienen sentido
las matrices producto: (AB)C y A(BC) ambas de orden m. Hagamos AB = [d
ij
]
mp
, BC = [e
ij
]
n
,
(AB)C = [f
ij
]
m
y A(BC) = [g
ij
]
m
. Debemos mostrar que para todo i = 1, , m y cada j = 1, ,
vale f
ij
= g
ij
. En efecto, de la denici on de multiplicaci on de matrices tenemos que
f
ij
=
p
k=1
d
ik
c
kj
y g
ij
=
n
s=1
a
is
e
sj
, donde d
ik
=
n
s=1
a
is
b
sk
y e
sj
=
p
k=1
b
sk
c
kj
,
de esta forma:
f
ij
=
p
k=1
_
n
s=1
a
is
b
sk
_
c
kj
=
p
k=1
_
n
s=1
a
is
b
sk
c
kj
_
=
n
s=1
_
p
k=1
a
is
b
sk
c
kj
_
=
n
s=1
a
is
_
p
k=1
b
sk
c
kj
_
=
n
s=1
a
is
e
sj
= g
ij
;
con lo cual (AB)C = A(BC).
7. Sean A = [a
ij
]
mn
y B = [b
ij
]
np
; luego es claro que A
t
= [e
ij
]
nm
y B
t
= [f
ij
]
pn
, donde e
ij
= a
ji
para todo i = 1, , n y j = 1, , m; y f
ij
= a
ji
para todo i = 1, , p y j = 1, , n. Observe que
2.4. Operaciones con matrices 19
tienen sentido las matrices matrices producto AB y B
t
A
t
. Si hacemos AB = [c
ij
]
mp
y B
t
A
t
= [d
ij
]
pm
,
entonces para cada i = 1, , m y j = 1, , p tenemos:
c
ij
=
n
k=1
a
ik
b
kj
y d
ij
=
n
k=1
f
ik
e
kj
.
Dado que al hacer (AB)
t
= [h
ij
]
pm
, tenemos h
ij
= c
ji
para todo i = 1, , p y j = 1, , m, entonces
para demostrar la propiedad 7 es suciente vericar que h
ij
= d
ij
para todo i = 1, , m y j = 1, , p.
En efecto:
h
ij
= c
ji
=
n
k=1
a
jk
b
ki
=
n
k=1
e
kj
f
ik
=
n
k=1
f
ik
e
kj
= d
ij
;
por tanto (AB)
t
= B
t
A
t
.
Comentario 2.6. Tal y como se observa en la denici on 2.13, para que tenga sentido la multiplicaci on
de dos matrices cualesquiera, digamos A y B, el n umero de columnas de A y el n umero de las de B
deben coincidir para as obtener la matriz producto AB. Por tanto, para tengan sentido al mismo tiempo
las matrices AB y BA es necesario y suciente que ambas tengan el mismo n umero de las como de
columnas; esto es, que ambas sean cuadradas del mismo orden. En particular, al considerar cualquier
matriz A M
mm
(K), siempre tienen sentido las matrices productos A
2
= AA, A
3
= AAA, y en
general, para cada entero positivo n 1, tiene sentido la potencia A
n
= AA A
. .
n veces
. Por conveniencia
se adopta que A
0
= I
m
. Note que para todo entero n 1 vale A
n
= AA
n1
. As en particular, si
A, B M
mm
(K), entonces tienen sentido, por ejemplo, expresiones como: (A + B)
2
, A
3
+ AB
2
, etc.
Dado que la multiplicaci on de matrices no es una operaci on conmutativa; es decir, no siempre vale
AB = BA (aunque ambas sean cuadradas del mismo orden), entonces f ormulas cl asicas como las del
binomio de Newton: (A + B)
2
= A
2
+ 2AB + B
2
, en general no son verdaderas cuando de trata de
matrices. De hecho puede demostrarse que (A+ B)
2
= A
2
+ 2AB +B
2
si, y s olo si, AB = BA.
Considerando entonces la posibilidad de tener potencias A
k
con A una matriz cuadrada y k un entero
no negativo, surge la inquietud sobre la posibilidad de poder tener expresiones como A
1
. En efecto,
esto es posible; pero no todas las matrices cuadradas son candidatas para poder efectuar este tipo de
potenciaci on; tal y como veremos a continuaci on
2.4.3. Matrices Invertibles
Denici on 2.14. Dada cualquier matriz A M
mm
(K), se dice que A es invertible (tambien se conoce
como no singular) si existe una matriz B M
mm
(K) tal que AB = BA = I
m
.
Ejemplo 2.11.
1. La matriz identidad I
m
de orden m m para cualquier m 1 es invertible, pues I
m
I
m
= I
m
, ver
teorema 2.2.
2. La matriz nula O
m
de orden m m es no invertible (o singular) pues cualquiera sea la matriz
B M
mm
(K) se tiene que O
m
B = I
m
pues O
m
B = O
m
, ver teorema 2.2.
3. La matriz A =
_
1 1
1 2
_
es invertible pues para B =
_
2 1
1 1
_
se verica al realizar las operaciones
AB y BA que AB = BA =
_
1 0
0 1
_
.
20 2.
Algebra Matricial
4. No toda matriz diferente de la matriz nula es invertible. Por ejemplo consideremos A =
_
1 2
0 0
_
.
Dado que esta matriz tiene una la nula, cualquiera sea la matriz B M
22
(C), el producto AB
tiene al menos la segunda la nula. En efecto; si hacemos B =
_
a b
c d
_
, entonces:
AB =
_
1 2
0 0
_ _
a b
c d
_
=
_
1 a + 2 c 1 b + 2 d
0 a + 0 c 0 b + 0 d
_
=
_
a + 2c b + 2d
0 0
_
.
En consecuencia es imposible que exista B M
22
(C) tal que AB =
_
1 0
0 1
_
. Similarmente se
muestra que si A tiene una columna nula, entonces no es invertible. De hecho esto es una propiedad
general; es decir, si A M
mm
(K) tiene al menos una la, o una columna nula, entonces A no es
invertible; ver ejercicio propuesto 21 en la p agina 40.
Finalizamos este ejemplo con la siguiente observaci on: para la matriz A =
_
1 2
0 0
_
elegimos B de
manera que a + 2c = 0 y b + 2d = 0, entonces AB = O
22
; por ejemplo, B =
_
2 2
1 1
_
tiene
esta propiedad. Esto muestra que el producto de dos matrices no nulas, no necesariamente es no
nula, de hecho AB =
_
1 2
0 0
_ _
2 2
1 1
_
=
_
0 0
0 0
_
.
Comentario 2.7. Los problemas de existencia, tanto en la Matem atica como en otras ciencias, pueden
tornarse problemas de difcil decisi on u obtenci on. La situaci on en el caso de matrices no deja de ser dife-
rente; por ello es necesario conocer y dominar algunas herramientas extras, adicionales a la multiplicaci on
de matrices, que permitan abordar el problema de responder a la cuesti on de si una matriz cuadrada dada
es o no invertible; y en caso de serlo, c omo obtener una matriz B que satisfaga la condici on expresada
en la denici on anterior. Una de tales herramientas ser a expuesta y desarrollada m as adelante. A ttulo
de motivaci on, supongamos que queremos saber si la matriz A =
_
2 1
1 1
_
es o no invertible. Claramente
para poder tomar una decisi on debemos conseguir una matriz B =
_
a b
c d
_
, que en particular satisfa-
ga AB =
_
1 0
0 1
_
. Esta ultima identidad conduce inmediatamente, luego de realizar la multiplicaci on e
igualar matrices, al problema de obtener escalares a, b, b y d que de manera simult anea satisfagan las
siguientes ecuaciones
_
_
2a +c = 1
2b +d = 0
a +c = 0
b +d = 1
.
Antes de emprender la tarea de conocer las herramientas necesarias para abordar este tipo de problemas,
conoceremos algunas propiedades b asicas sobre matrices invertibles.
Teorema 2.3. Dadas matrices A, B M
mm
(K), se satisfacen las siguientes propiedades:
1. (Unicidad de la inversa) Si A M
mm
(K) es invertible, entonces existe una unica matriz
P M
mm
(K) tal que AP = PA = I
m
; esto es, si hay una otra matriz Q M
mm
(K) tal que
AQ = QA = I
m
, entonces P = Q.
2.4. Operaciones con matrices 21
Esto establece la unicidad de las matrices P M
mm
(K) que satisfacen la identidad AP = PA = I
m
.
Por tanto, en adelante, si A M
mm
(K) es invertible, a la unica matriz P M
mm
(K) que satisface
AP = PA = I
m
la denominamos inversa de A y la denotamos por A
1
.
2. Si A M
mm
(K) es invertible, entonces A
1
tambien lo es, y (A
1
)
1
= A.
3. Si A M
mm
(K) y B M
mm
(K) son invertibles, entonces AB tambien es invertible y se cumple
que (AB)
1
= B
1
A
1
.
4. Si A M
mm
(K) es tal que AP = I
m
y QA = I
m
, entonces P = Q y A es invertible; de hecho,
A
1
= P = Q.
5. Dada A M
mm
(K) es invertible. Si X, Y M
m1
(K) son tales que AX = AY , entonces X = Y .
Adem as, para cualquier Y M
m1
(K), existe X M
m1
(K) tal que AX = Y .
Demostraci on:
1. Supongamos que A es invertible y que existen dos matrices P, Q M
mm
(K) satisfaciendo que
PA = AP = I
m
= QA = AQ. Luego, usando estas identidades sigue inmediatamente:
P = P I
m
= P(AQ) = (P A)Q = I
m
Q = Q.
2. Sean A M
mm
(K) invertible y A
1
la unica matriz en M
mm
(K) que satisface AA
1
= A
1
A = I
m
;
esto es, la inversa de A. Entonces de la misma denici on tenemos que A
1
es invertible y A = (A
1
)
1
es la unica matriz que multiplicada tanto a la derecha como a la izquierda de A
1
resulta la identidad.
3. Sean A, B M
mm
(K) invertible y A
1
, B
1
M
mm
(K) sus respectivas inversas. Mostrar que AB
es invertible signica encontrar una matriz C en M
mm
(K) tal que (AB)C = I
m
= C(AB); en tal caso
C es la inversa de AB; es decir, C = (AB)
1
. Tomemos C = B
1
A
1
, y veamos que tal matriz satisface
lo requerido. En efecto:
(AB)C = (AB)(B
1
A
1
) = A(BB
1
)A
1
= AI
m
A
1
= AA
1
= I
m
;
de la misma forma se verica C(AB) = I
m
. Por tanto, AB es invertible y (AB)
1
= B
1
A
1
.
4. Se deja como ejercicio para el lector. Note que esta propiedad dice que si una matriz cuadrada tiene
una inversa a la izquierda y otra a la derecha, entonces la matriz es invertible y las inversas laterales
coinciden.
5. Primero mostraremos que si AX = O
m1
, entonces X = O
m1
. En efecto, sea X M
m1
(K) tal que
AX = O
m1
. Dado que A es invertible, existe A
1
M
mm
(K) tal que AA
1
= I
m
= A
1
A. Luego, al
multiplicar AX = O
m1
a ambos lados por A
1
, y por la izquierda, tenemos:
X = I
m
X = (A
1
A)X = A
1
(AX) = A
1
O
m1
= O
m1
.
Supongamos ahora que X, Y M
m1
(K) son tales que AX = AY . Sigue por tanto que
AX AY = A(X Y ) = O
m1
(por que?)
Por tanto X Y = O
m1
; es decir, X = Y .
Dejamos al lector la tarea de vericar que bajo la misma hip otesis de invertibilidad de la matriz
A, se cumple que si para Y M
m1
(K) dado, existe X M
m1
(K) tal que AX = Y , entonces tal
X M
m1
(K) es unico.
22 2.
Algebra Matricial
Comentario 2.8. Como hemos visto, por denici on, para que una matriz cuadrada A M
mm
(K) sea
invertible se requiere que exista B M
mm
(K) tal que AB = BA = I
m
. En realidad esta denici on se
puede haber expresado diciendo:
Denici on 2.15. Una matriz A M
mm
(K) es invertible si existe B M
mm
(K) de manera que se
cumplan alguna de las siguientes dos condiciones: AB = I
m
o BA = I
m
En Matem atica, en cualquier ciencia, cuando se ofrecen dos, o m as, deniciones de una misma propie-
dad, se debe demostrar que tales deniciones son equivalentes. En el caso particular que estamos tratando,
es obvio que la denici on 2.14 implica la denici on 2.15. Realmente la segunda denici on tambien implica
la primera; es decir, son equivalentes. Pero para dar una demostraci on de esta segunda implicaci on se
requiere de un poco m as de desarrollo te orico, el cual ser a abordado en la siguiente secci on.
2.5. Operaciones Elementales por las y Matrices Elementales
Lo que denominaremos operaciones elementales por las son tres tipos de operaciones que deniremos
sobre el conjunto de todas las matrices de orden m n sobre el cuerpo K, cualesquiera sean los enteros
positivos m y n. Esta nuevas operaciones constituyen una herramienta muy util para efectuar una amplia
variedad de c alculos que son empleados usualmente en los cursos b asicos de
Algebra Lineal; por ejemplo,
el uso de estas operaciones elementales por las permitir a decidir, de manera muy simple, cu ando una
matriz cuadrada dada es o no invertible; adem as, en el caso de ser invertible tambien ofecer a una tecnica
de obtenci on de su inversa. Las operaciones elementales por la tambien ofrecer an herramientas de c alculo
para abordar la resoluci on de sistemas de ecuaciones lineales.
2.5.1. Denici on, ejemplos y propiedades generales
Denici on 2.16. Una operaci on elemental por las es cualquier correspondencia M
mn
(K) M
mn
(K)
que asocia a cada matriz A M
mn
(K) una matriz en M
mn
(K) de alguno de los siguientes tipos:
Tipo I: multiplicaci on de una la de A por un escalar K\{0}. La notaci on f
i
f
i
signica
que la la i se multiplica por el escalar no nulo .
Tipo II: sustituci on de una la de A por la suma de dicha la y un m ultiplo no nulo de otra de
las las de A. La nomenclatura f
i
f
i
+ f
j
dice que la la la i se sustituye por la suma de la
la i y veces la la j, con diferente de 0.
Tipo III: transposici on de dos de las las de la matriz A. Esta operaci on elemental se denota por
f
i
f
j
, lo cual indica que las las i y j se intercambian.
Ejemplo 2.12.
1. El resultado de aplicar la operaci on f
1
2 f
1
sobre la matriz
_
2 1 0
0 3 1
_
es la matriz
_
4 2 0
0 3 1
_
;
esto se simboliza mediante:
_
2 1 0
0 3 1
_
f
1
2f
1
_
4 2 0
0 3 1
_
.
2.
_
_
2 1 0
0 3 1
0 0 2
_
_
f
2
f
2
+2f
3
_
_
2 1 0
0 3 5
0 0 2
_
_
indica que se ha aplicado a la matriz
_
_
2 1 0
0 3 1
0 0 2
_
_
la operaci on
elemental por las f
2
f
2
+ 2f
3
; es decir, la segunda la se ha sustituido por ella m as dos veces
la tercera la.
2.5. Operaciones Elementales por las y Matrices Elementales 23
3. Mientras que al aplicar la operaci on f
2
f
3
a
_
_
2 1 0
0 3 1
0 0 2
_
_
se obtiene
_
_
2 1 0
0 0 2
0 3 1
_
_
. Esto se denota
por
_
_
2 1 0
0 3 1
0 0 2
_
_
f
2
f
3
_
_
2 1 0
0 0 2
0 3 1
_
_
.
Teorema 2.4. Dada una operaci on elemental por las e : M
mn
(K) M
mn
(K), en adelante oef, existe
otra oef del mismo tipo, e
1
: M
mn
(K) M
mn
(K), tal que para toda matriz A M
mn
(K) se tiene
e
1
(e(A)) = A y e(e
1
(A)) = A. Es decir, las oef son aplicaciones invertibles y sus inversas son tambien
oef, y adem as del mismo tipo.
3
Demostraci on: Supongamos que e : M
mn
(K) M
mn
(K) es la oef del Tipo I que la i-esima la de
cada matriz A de M
mn
(K) es sustituida por el producto del escalar K\{0} y la la i de A; es decir,
e es la oef f
i
f
i
. Consideremos ahora la oef e
1
: M
mn
(K) M
mn
(K) dada por f
i
1
f
i
.
Veamos que e
1
(e(A)) = A y e(e
1
(A)) = A. En efecto, sea A cualquier matriz de M
mn
(K); observe que
las oef e y e
1
unicamente alteran la la i (las restantes quedan iguales); de hecho, la la i de e(A) es
A
(i)
, mientras que la la i de e
1
(A) es
1
A
(i)
. Por tanto, al aplicarle e
1
a e(A), la la i de la nueva
matriz e
1
(e(A)) es el producto de
1
por la la i de e(A); esto es,
1
(A
(i)
), lo cual implica que la la
i de e
1
(e(A)) es justamente la la i de A; y como las restantes las (las diferentes de i) no tienen ninguna
alteraci on, concluimos que e
1
(e(A)) = A. De la misma forma se verica e(e
1
(A)) = A. Con lo cual la oef
f
i
f
i
tiene como inversa a la oef f
i
1
f
i
, que obviamente es del mismo Tipo I.
De forma similar se muestra que las oef de los tipos II y III tambien son invertibles; de hecho, la oef
del Tipo II f
i
f
i
+f
j
tiene como inversa a la oef f
i
f
i
f
j
; mientras que la inversa de la oef
del Tipo III f
i
f
j
es ella misma. Se dejan los detalles al lector.
Denici on 2.17. Dadas matrices A, B M
mn
(K), se dice que A es equivalentes por las B, se donota
A
oef
B, si existe una secuencia nita de oef que permite obtener B a partir de A. Es decir, si existe
un entero k 1 y oef e
1
, e
2
, , e
k
tales que (e
1
e
2
e
k
)(A) = B; simb olicamente se escribe
A
e
1
A
1
e
2
A
2
e
k1
A
k1
e
k
B.
Ejemplo 2.13. Para las matrices A =
_
_
0 1 3
0 1 1
2 1 4
_
_
y B =
_
_
2 1 4
0 1 1
0 0 4
_
_
se tiene A
oef
B. En
efecto:
A =
_
_
0 1 3
0 1 1
2 1 4
_
_
f
1
f
3
_
_
2 1 4
0 1 1
0 1 3
_
_
f
3
f
3
f
2
_
_
2 1 4
0 1 1
0 0 4
_
_
= B.
Comentario 2.9. Supongamos que A, B M
mn
(K) son tales que A
oef
B; es decir, existen oef
e
1
, e
2
, , e
k
tales que (e
1
e
2
e
k
)(A) = B. Entonces tambien se tiene que B
oef
A; es decir, tambien
existen oef que permiten ir desde B hacia A; en otras palabras, la relaci on binaria
oef
es una relaci on
simetrica. Esto sigue de los siguientes hechos: primero, las oef son invertibles y sus inversas son tambien
oef (es m as, del mismo tipo); y segundo, cualesquiera sean las funciones invertibles f
1
, f
2
, , f
k
: A A,
la funci on composici on f
1
f
2
f
k
: A A es invertible, y su inversa (f
1
f
2
f
k
)
1
satisface:
(f
1
f
2
f
k
)
1
= f
1
k
f
1
2
f
1
1
.
3
Recuerde que una funci on f : A B (A y B son conjuntos cualesquiera) es invertible si, y s olamente si, existe otra
funci on g : B A tal que, para todo a A y todo b B se satisfacen: (g f)(a) = a y (f g)(b) = b
24 2.
Algebra Matricial
Por tanto, si (e
1
e
2
e
k
)(A) = B, al aplicar la inversa (e
1
e
2
e
k
)
1
a ambos lados por la
izquierda, tenemos:
A = (e
1
e
2
e
k
)
1
(B) = (e
1
k
e
1
2
e
1
1
)(B);
por lo que B
oef
A.
El siguiente resultado dice algo m as que la propiedad de simetra de
oef
.
Teorema 2.5. La equivalencia por las
oef
en el conjunto M
mn
(K) es una relaci on de equivalencia:
1. toda matriz de M
mn
(K) es equivalente por las a s misma, A
oef
A. (reexividad);
2. si A M
mn
(K) es equivalente por las a B M
mn
(K), entonces B es equivalente por las a A;
es decir, A
oef
B = B
oef
A (simetra); y
3. si A M
mn
(K) es equivalente por las a B M
mn
(K) y B es equivalente por las a C en
M
mn
(K), entonces A es equivalente por las a C; esto es: (A
oef
B y B
oef
C) = A
oef
C.
(transitividad)
Demostraci on: La reexividad de
oef
sigue inmediatamente del hecho que toda oef es invertible y su
inversa es otra oef; por tanto si e y e
1
son oef, una la inversa de la otra, entonces (e e
1
)(A) = A para
toda matriz A M
mn
(K); es decir, A
oef
A. La simetra de
oef
fue demostrada en el comentario
anterior. Dejamos la vericaci on de la transtividad al lector.
A raz de la propiedad de simetra que posee la relaci om binaria
oef
, en lugar de decir que A es
equivalente por las a B, simplemente diremos que A y B son equivalentes por las; pues en presencia
de A
oef
B, tambien se tiene B
oef
A.
Denici on 2.18. Una matriz cuadrada E M
mm
(K) se dice matriz elemental si existe una oef e tal
que E = e(I
m
). Es decir, una matriz elemental es el resultado de aplicar una s ola (cualquiera) oef a la
matriz identidad.
Ejemplo 2.14. Las siguientes matrices son elementales:
_
2 0
0 1
_
,
_
_
1 0 0
0 1 3
0 0 1
_
_
,
_
_
1 0 0
0 0 1
0 1 0
_
_
pues todas se obtienen de una matriz identidad a traves de una s ola operaci on elemental por las; en
efecto, la primera se obtiene al aplicarle a I
2
la operaci on f
1
2 f
1
; la segunda y tercera de I
3
al
aplicarles, respectivamente, las operaciones: f
2
f
2
+ 3 f
3
y f
2
f
3
.
Teorema 2.6. Dadas A M
mn
(K) y una operaci on elemental por las e, si E es la matriz elemental
correspondiente a e; esto es, E = e(I
m
), entonces EA = e(A).
Demostraci on: La demostraci on se debe hacer considerando cada uno de los tipos de oef. Supongamos
que e es una oef del Tipo I, es decir, e es de la form f
i
f
i
, donde i es alg un ndice entre 1 y m, y
K\ {0}. Claramente, como E se obtiene de I
m
al aplicarle e, entonces las las de E, E
(1)
, , E
(m)
,
son: E
(r)
= [0 0 1 0 0], siempre que r sea distinto de i y la entrada no nula es la r-esima; mientras
que la la i-esima de E es E
(i)
= [0 0 0 0], donde la entrada no nula es la i-esima. Recordemos
que en el item 4 del ejemplo 2.10, ver p agina 16, se mostr o que al multiplicar por la izquierda cualquier
matriz unila can onica por cualquier matriz A, da como resultado la la de A correspondiente al ndice
2.5. Operaciones Elementales por las y Matrices Elementales 25
de tal matriz can onica unila. De manera pues que al realizar la multiplicaci on EA, tenemos que las las
r, con r = i, son las correspondientes las de A; es decir, EA
(r)
= A
(r)
, con r = i, y la la i-esima de EA
se obtiene como el producto EA
(i)
A; de manera simple se verica que este producto es justamente la la
i de A multiplicada por el escalar . De esta forma, EA es la misma matriz que se obtiene al aplicar la
operaci on elemental e a la matriz A.
Las vericaciones del teorema con oef de los tipos II y III se dejan como ejercicio al lector.
Corolario 2.1. Sean A, B M
mn
(K) con A
oef
B y e
1
, , e
k
oef tales que (e
1
e
k
)(A) = B.
Si E
1
, , E
k
son las respectivas matrices elementales correspodientes a las oef e
1
, , e
k
; esto signica,
E
i
= e
i
(I
m
) para cada i = 1, , m, entonces E
1
E
k
A = B.
Demostraci on: La demostraci on sigue por inducci on sobre el entero k a partir del teorema 2.6. Cla-
ramente, el enunciado del corolario es verdadero para k = 1 (es la conclusi on del teorema anterior!).
Supongamos como v alido el enunciado del corolario (hip otesis inductiva) para todo valor entero de k
entre 1 y 1. Vamos a demostrar ahora que tambien es verdadero cuando k = .
Sean e
1
, , e
oef tales que (e
1
e
)(A) = B, y sean E
i
= e
i
(I
m
) con i = 1, , las matrices
elementales correspondientes. Luego:
B = (e
1
e
)(A) = (e
1
e
1
)(e
(A)) (por que?)
= (e
1
e
1
)(E
A) = (E
1
E
1
)E
A (por que?)
= E
1
E
1
E
A;
por tanto la demostraci on est a completa.
Corolario 2.2. Si A, B M
mn
(K) son equivalentes por las, entonces existe una matriz invertible
F M
mm
(K) tal que F A = B.
Demostraci on: Del corolario anterior tenemos que existe un n umero nito de matrices elementales
E
1
, , E
k
, todas de orden mm, tales que E
1
E
k
A = B. Como cada matriz elemental es invertible
y el producto de matrices invertible, entonces el corolario sigue.
Corolario 2.3. Toda matriz elemental es invertible, y su inversa es tamben una matriz elemental.
Demostraci on: Sean E M
mm
(K) la matriz elemental dada por la oef e; es decir, E = e(I
m
). Del
teorema anterior sabemos que para cualquier matriz A M
mm
(K) se cumple EA = e(A). Considere
ahora la oef f que es la inversa de e, y sea F la matriz elemental correspondiente; esto es, F = f(I
m
).
Luego como EA = e(A) vale para toda A M
mm
(K), en particular se tiene EF = e(f(I
m
)), pero
e(f(I
m
)) = I
m
pues e y f son una la inversa de la otra. As, EF = I
m
y de la misma forma se muestra
que FE = I
m
; con lo cual la demostraci on del corolario est a completa.
Ejemplo 2.15.
1. Consideremos la matriz A =
_
2 1 0 1
3 2 3 0
_
y la operaci on elemental que sustituye la segunda
la por la suma de tal la y menos una vez la primera la; esta es e = f
2
f
2
+ (1)f
1
.
Claramente, la matriz obtenida a partir de A luego de aplicarle una vez esta operaci on elemental
es e(A) =
_
2 1 0 1
1 1 3 1
_
. Por otro lado, la matriz elemental de orden 2 2 asociada a e es
26 2.
Algebra Matricial
E =
_
1 0
1 1
_
. De esta forma tenemos que
EA =
_
1 0
1 1
_ _
2 1 0 1
3 2 3 0
_
=
_
2 1 0 1
1 1 3 1
_
= e(A).
2. Las matrices A =
_
_
2 1 1 5
0 1 2 0
1 1 3 4
_
_
y B =
_
_
1 1 3 4
0 1 2 0
0 0 13 13
_
_
son equivalentes por las
pues:
A
f
1
f
3
_
_
1 1 3 4
0 1 2 0
2 1 1 5
_
_
f
3
f
3
2 f
1
_
_
1 1 3 4
0 1 2 0
0 3 7 13
_
_
f
3
f
3
3 f
2
B.
Como hemos empleado las operaciones e
1
= f
1
f
3
, e
2
= f
3
f
3
2 f
1
y e
3
= f
3
f
3
3 f
2
,
las matrices elementales de orden 3 3 correspondientes a cada una de ellas respectivamente son
E
1
=
_
_
0 0 1
0 1 0
1 0 0
_
_
, E
2
=
_
_
1 0 0
0 1 0
2 0 1
_
_
y E
3
=
_
_
1 0 0
0 1 0
0 3 1
_
_
,
entonces se tiene que E
3
E
2
E
1
A = B ya que (e
3
e
2
e
1
)(A) = B.
3. Consideremos la oef e : M
22
(K) M
22
(K) dada por f
2
f
2
+2f
1
; entonces la matriz elemental
correspondiente a e es E =
_
1 0
2 1
_
. Dado que la oef f dada por f
2
f
2
2f
1
es la inversa de e,
sigue que la matriz elemental F =
_
1 0
2 1
_
, que es asociada a f, satisface EF = FE =
_
1 0
0 1
_
;
es decir, E
1
= F y F
1
= E.
2.5.2. Forma can onica de Gauss-Jordan
Antes de introducir lo que denominaremos forma can onica de Gauus-Jordan de matrices de orden
mn, es conveniente hacer una revisi on de algunas de las implicaciones algebraicas que trae consigo la
existencia de una relaci on de equivelencia.
Supongamos que sobre el conjunto no vaco A est a denida una relaci on de equivalencia ; esto es:
reexiva, simetrica y transitiva (ver teorema 2.5). Asociada a una tal relaci on se introduce el concepto
de clase de equivalencia.
Denici on 2.19. Dado a A, se denomina clase de equivalencia de a, lo denotamos por [a]
, al conjunto
[a]
= {b A : a b};
es decir, la clase de equvalencia de a, es el conjunto de elementos de A que est an relacionados con a seg un
la relaci on .
Claramente por la reexividad, para todo a A se cumple a [a]
; por tanto las clases de equi-
valencias son subconjuntos no vacos de A. Por otra parte, se puede demostrar que para cualquier par
a, b A se cumple s olamente una de las dos siguientes opciones: o [a]
= [b]
, o bien [a]
[b]
= ; es
2.5. Operaciones Elementales por las y Matrices Elementales 27
decir, dos clases de equivalencias de uma misma relaci on, o son iguales, o disjuntas. Esto en realidad es
consecuencia de la siguiente propiedad: dados a, b A, se cumple a b si, y s olo si, [a]
= [b]
. De esta
forma, dado que A =
_
aA
[a]
(verifquelo!), entonces las clases de equivalencias diferentes que existen
dividen al conjunto A en partes que son disjuntas; esto se denomina una partici on de A, la partici on
inducida por . Finalmente, supongamos que tenemos [a]
; a cualquier elemento b [a]
(entre ellos el
propio a) se le conoce como representante de la clase de equivalencia [a]
.
Retornando a la clase de equivalencia
oef
sobre el conjunto de matrices M
mn
(K), la dada por
las oef; lo que deseamos es encontrar representantes simples de cada clase. De hecho, encontraremos
una matriz para cada clase de equivalencia, y la denominaremos forma can onica de Gauss-Jordan, la
cual tambien es conocida de otras formas, por ejemplo, matriz escalonada reducida por las, o forma
reducida por las; ac a adoptamos la denominaci on Gauss-Jordan en honor a: Carl Friedrich Gauss,
matem atico alem an (1777-1855), conocido como el principe de los matem aticos; y al tambien alem an
Wilhelm Jordan (1842-1899) especialista en Geodesia
4
; justamente la primera vez que aparece publicado
lo referente a matrices (y el metodo) de Gauss-Jordan fue en un libro de Geodesia escrito por Wilhelm
Jordan; por tanto, no debe confundirse este Jordan con el famoso matem atico frances Camille Jordan
(1838-1922) que trabaj o sobre teora de matrices.
Denici on 2.20. Una matriz A M
mn
(K) se dice escalonada si es la matriz nula, o de lo contrario
satisface las dos siguientes propiedades:
las las nulas son las ultimas; y
si a
1j
1
, a
2j
2
, , a
rj
r
son las primeras entradas no nulas de cada la no nula, las cuales son deno-
minadas pivotes de A, entonces j
1
< j
2
< < j
r
.
Toda matriz escalonada de orden mn con entradas en K es de la forma:
_
_
0 0 a
1j
1
0 0 0 0 a
2j
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 0 0 a
rj
r
0 0 0 0 0 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 0 0 0 0
_
_
, (2.10)
donde lo se nalado con * indica que tal posici on puede estar ocupada por cualquier valor en K. Esto es,
A tiene una forma escalonada descendiente de izquiera a derecha, formada por sus entradas nulas.
Ejemplo 2.16.
1. La matriz identidad de cualquier orden es escalonada, en crculo se idican los elementos pivotes de
I
3
; que son las entradas no nulas en cada la no nula.
_
_
1 0 0
0 1 0
0 0 1
_
_
.
4
Ciencia que trata de la forma y dimensi on de la Tierra
28 2.
Algebra Matricial
2. La matriz
_
_
2 3 4 1
0 0 0 1
0 0 0 0
0 0 0 0
_
_
es escalonada, los pivotes est an encerrados en crculos.
3. Toda matriz triangular superior cuyas entradas en la diagonal sean todas diferentes de 0 es una
matriz escalonada. Es cierto la misma armaci on si algunas de las entradas en la diagonal es nula?
Son escalonadas las matrices triangulares inferiores, diagonales y escalares?
4. Las siguientes matrices no son escalonadas, por que?:
_
_
0 2 0
1 0 1
0 0 0
0 0 0
_
_
,
_
_
1 2 0
0 3 0
2 0 0
_
_
,
_
_
2 0 0 3
0 0 0 0
0 0 0 1
_
_
,
_
_
0 0 0 3
1 0 1 0
0 0 0 0
_
_
,
_
_
0 0 0 0 0
0 0 0 0 0
0 3 1 2 0
0 0 2 1 0
0 0 0 3 0
_
_
.
Teorema 2.7. Dada cualquier matriz A M
mn
(K), existe una matriz escalonada que es equivalente
por las a la matriz A.
Demostraci on: La demostraci on de este teorema es algortmica. Sea A una matriz en M
mn
(K). Si A
es la matriz nula, no hay que hacer nada, ya es una matriz escalonada. Supongamos entonces que A es
no nula, entonces procedemos de acuerdo a los siguientes pasos (este es el algoritmo):
Paso 1: Se inicializa un contador: k = 1
Paso 2:
Si las las por debajo de la la k son nulas, entonces tal matriz ya es
escalonada, y la demostraci on est a completa. Caso contrario, se emplean
oef del Tipo III para: colocar las las nulas en las posiciones nales, y
en la la k se coloca una la de forma que el ndice de columna de su
primera entrada no nula sea menor o igual que el ndice de columna de
la primera entrada no nula de las restantes las no nulas.
Paso 3:
Mediante oef de Tipo II, f
i
f
i
f
k
( = 0), se anulan todas las
entradas que est an debajo de la primera entrada no nula de la la k.
Paso 4: Se hace k k + 1 y se va al Paso 2
Dado que la matriz A tiene un n umero nito de las (m en este caso), entonces el algoritmo es nito;
por tanto la matriz as obtenida es escalonada y equivalente por las a la matriz inicial A.
Comentario 2.10. Observe que la demostraci on que acabamos de presentar, en tanto que es algoritmica,
no es la unica forma de obtener una matriz escalonada equivalente por las a la matriz dada. Por otra
parte, suponiendo que mediante este algoritmo, o cualquier otro, se ha obtenido una matriz escalonada
B
oef
A, mediante oef del Tipo I, los pivotes de B, digamos B
ij
i
, con i = 1, , r y j
1
< j
2
< < j
r
,
podemos hacerlos iguales a 1, pues todos ellos son diferentes de 0; adem as, usando operaciones elementales
del Tipo II se pueden hacer 0 las entradas ubicadas por encima de estos pivotes, lo cual ofrece otra matriz
escalonada equivalente a A.
2.5. Operaciones Elementales por las y Matrices Elementales 29
Ejemplo 2.17. Vamos a obtener una matriz escalonada equivalente por las a A =
_
_
0 0 0 0
2 2 1 3
4 0 2 6
0 3 0 2
2 0 1 3
_
_
.
A =
_
_
0 0 0 0
2 2 1 3
4 0 2 6
0 3 0 2
2 0 1 3
_
_
f
1
f
5
_
2 0 1 3
2 2 1 3
4 0 2 6
0 3 0 2
0 0 0 0
_
_
f
2
f
2
+f
1
f
3
f
3
2 f
1
_
_
2 0 1 3
0 2 0 6
0 0 0 0
0 3 0 2
0 0 0 0
_
_
f
3
f
4
_
2 0 1 3
0 2 0 6
0 3 0 2
0 0 0 0
0 0 0 0
_
_
f
3
f
3
3
2
f
2
_
2 0 1 3
0 2 0 6
0 0 0 11
0 0 0 0
0 0 0 0
_
_
,
que es una matriz escalonada y equivalente por las a A. Observe que no es la unica de tales matrices;
pues haciendo 1 las entradas encerradas en crculos se obtiene otra matriz escalonada equivalente por
las a A; vea el comentario anterior.
El siguiente teorema, cuya demostraci on puede incluso ser obviada, es importante pues introduce
un invariante (propiedad com un a una cierta clase de matrices) en las matrices escalonadas que son
equivalentes por las.
Teorema 2.8. Sean A y B matrices escalonadas cualesquiera en M
mn
(K) tales que A
oef
B, entonces
el n umero de las no nulas (y por tanto el n umero de las nulas) en ambas es el mismo.
Demostraci on: Del corolario 2.2 existe una matriz invertible E M
mm
(K) tal que EA = B. Obvia-
mente si alguna de estas matrices, A o B, es nula, entonces la otra tambien; por tanto no habra nada
que demostrar. Supongamos entonces que ambas son nulas.
Sean r 1 y r
1 el n umero de las no nulas de A y B respectivamente. Sean j
1
< < j
r
y
j
1
< < j
r
los ndices de las columnas de A y B, respectivamente, que contienen los pivotes de B y
C. Observe que en tales columnas, las entradas ubicadas debajo de los pivotes son iguales a 0. Adem as
de demostrar que r = r
, tambien mostraremos que los ndices de las columnas donde est an los pivotes
de A y B son los mismos; esto es, para cada k = 1, , r se tiene j
k
= j
k
.
Supongamos que r r
; caso contrario invertimos los papeles de A y B, y as tenemos las condici on.
Note que las columnas de A, A
(j)
, con ndices 1 j < j
1
son todas nulas. Dado que B = EA y cada
columna j de B, satisface B
(j)
= EA
(j)
, entonces las columnas B
(j)
de B, con 1 j < j
1
, son todas
nulas. Esto implica que j
1
j
1
. Empleando el mismo argumento al cambiar A por B y E por F = E
1
se obtiene j
1
j
1
, de donde j
1
= j
1
.
Por otro lado, la columna A
(j
1
)
de A es A
(j
1
)
=
_
_
a
1j
1
0
.
.
.
0
_
_
= a
1j
1
e
(1)
, donde e
(k)
denota la k-esima
matriz unicolumna can onica. En vista de que B
(j
1
)
= EA
(j
1
)
se tiene B
(j
1
)
= Ea
1j
1
e
(1)
= b
1j
1
e
(1)
, con
30 2.
Algebra Matricial
b
1j
1
= 0; es decir,
Ee
(1)
=
11
e
(1)
, para alg un
11
= 0.
Observe que si r = 1; es decir que todas las columnas A
(j)
de A con j j
1
son de la forma a
1j
e
(1)
,
entonces de la identidad de arriba sigue que las columnas B
(j)
de B con j j
1
son de la forma b
1j
e
(1)
,
por tanto r
= 1 y la demostraci on estara completa. Supongamos entonces que r 2, es decir existe
j
2
> j
1
, las columnas A
(j)
de A para j
1
< j < j
2
son de la forma a
1j
e
(1)
, mientras que la columna
A
(j
2
)
=
_
_
a
1j
2
a
2j
2
0
.
.
.
0
_
_
= a
1j
2
e
(1)
+ a
2j
2
e
(2)
con a
2j
2
= 0. Esto implica, como antes, que las columnas B
(j)
de
B para j
1
< j < j
2
son de la forma b
1j
e
(1)
, de donde j
2
j
2
. Invirtiendo los papeles, de la misma
manera como fue indicado arriba, tenemos la desigualdad j
2
j
2
, de donde j
2
= j
2
. Adem as, como
B
(j
2
)
= EA
(j
2
)
, se deduce similarmente que:
Ee
(2)
=
21
e
(1)
+
22
e
(1)
, para ciertos
21
,
22
con
22
= 0.
Ahora procedemos por recurrencia; es decir, asumamos como cierto que para todo 1 k < r vale:
j
k
= j
k
y que Ee
(k)
=
k
j=1
kj
e
(j)
, donde
kk
= 0;
mostraremos que lo mismo vale para el ndice k +1. En efecto, las columnas A
(j)
de A con j
k
< j < j
k+1
tienen todas las entradas iguales a 0 entre la la k + 1 y la la m; es decir, A
(j)
=
k
i=1
ji
e
(i)
. Como
B
(j)
= EA
(j)
, entonces para cada j con j
k
< j < j
k+1
, la columna B
(j)
es sumatoria de m ultiplos de
e
(1)
, , e
(k)
; esto indica que tales columnas de C tienen todas las entradas iguales a 0 entre las las
k + 1 y la la m. Por tanto j
k+1
j
k+1
. Al invertir los papeles de A por B se tiene j
k+1
j
k+1
, con
lo cual j
k+1
= j
k+1
; lo cual demuestra que j
k
= j
k
y Ee
(k)
=
k
j=1
kj
e
(j)
, donde
kk
= 0 para todo
k = 1, , r.
Finalmente, las las r + 1, , m de A son todas nulas, esto dice que las columnas de A con ndices
j = j
r
+1, , n son sumatorias de multiplos de e
(1)
, , e
(r)
; por tanto, como B = EA, las columnas de
B m as all a de la columna j
r
son sumas de m ultiplos de e
(1)
, , e
(r)
. Luego es imposible que exista una
columna B
(j)
de B, con ndice superior a j
r
que tenga entradas no nulas por debajo de la la r; as r = r
y la demostraci on est a completa.
Denici on 2.21. Dada A M
mn
(K), se conoce con el nombre de rango de A, o tambien rango la de
A, al n umero de las no nulas que tiene cualquier matriz escalonada equivalente por las a A. Tal entero
no negativo se denota por rg(A).
Comentario 2.11. El teorema que acabamos de demostrar, y la denici on que ha permitido introducir,
constituyen un elemento b asico para entender varios procesos, tanto te oricos como de c alculo, que son
abordados empleando herramientas del
Algebra Lineal. Al respecto, es signicativo mencionar lo siguiente:
El rango es un invariante para las matrices que son equivalentes por las; esto es, cualquier par de
matrices que sean equivalente por las tienen el mismo rango; esto es justamente el teorema anterior.
Dada una matriz A M
mn
(K), su rango es un entero r con 0 r m; claramente la unica matriz
de rango 0 es la matriz nula.
2.5. Operaciones Elementales por las y Matrices Elementales 31
De la propia denici on de matriz escalonada sigue que el rango de cualquier matriz de orden m n
es siempre menor o igual al mn{m, n}. Se deja al lector la vericaci on de esta armaci on. Cuando una
matriz de orden mn tiene rango igual a mn{m, n}, se dice que tiene rango m aximo.
Dos matrices del mismo orden pueden tener el mismo rango, sin embargo no tienen porque ser equiva-
lentes por las. Por ejemplo, las matrices A =
_
2 0 1 4
0 1 0 4
_
y B =
_
2 0 1 4
0 0 1 4
_
tienen el mismo rango,
en este caso igual a 2, pero no son equivalentes por las ya que los ndices de las columnas donde est an
las primeras entradas no nulas de las las no nulas son diferentes; ver teorema anterior.
Ejemplo 2.18. Determinemos el rango de A =
_
_
2 0 1
1 1 2
3 1 3
1 1 2
_
_
. Lo que debemos hacer es obtener
una matriz equivalente por las a A que sea escalonada y luego contar el n umero de las no nulas de esta
ultima.
A
f
2
f
1
_
1 1 2
2 0 1
3 1 3
1 1 2
_
_
f
2
f
2
2 f
1
f
3
f
3
3 f
1
f
4
f
4
+ f
1
_
_
1 1 2
0 2 3
0 2 3
0 0 0
_
_
f
3
f
3
f
2
_
1 1 2
0 2 3
0 0 0
0 0 0
_
_
.
Luego el rango de A es igual a 2.
Denici on 2.22. Una matriz A M
mn
(K) se dice escalonada reducida por las si es nula, o en caso
contrario es: escalonada, los pivotes son todos iguales a 1 y las entradas arriba de los pivotes son nulas.
Toda matriz no nula escalonada reducida por las tiene la forma:
_
_
0 0 1 0 0
0 0 0 0 1 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 0 0 1
0 0 0 0 0 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 0 0 0 0
_
_
, (2.11)
siendo que lo se nalado con * indica que tal posici on puede estar ocupada por cualquier valor en K.
Ejemplo 2.19.
1. La matriz identidad de cualquier orden es claramente escalonada reducida por las.
2. La matriz
_
_
1 3 4 0
0 0 0 1
0 0 0 0
0 0 0 0
_
_
es escalonada reducida por las.
3. No todas las matrices escalonadas son reducidas por las; as como tampoco matrices cuyos pivotes
sean iguales a 1, siendo estos las unicas entradas no nulas en sus respectivas columnas. Las siguientes
32 2.
Algebra Matricial
matrices son ejemplos que demuestran estas armaciones.
_
_
4 3 4 0
0 0 0 1
0 0 0 0
0 0 0 0
_
_
,
_
_
1 0 0 0 1
0 0 0 1 2
0 1 0 0 3
0 0 1 0 3
0 0 0 0 0
0 0 0 0 0
_
_
.
4. Las siguientes matrices no son escalonadas reducidas por las, por que?:
_
_
0 1 0
1 0 1
0 0 0
0 0 0
_
_
,
_
_
1 0 0
0 3 0
0 0 0
_
_
,
_
_
1 0 0 0
0 0 0 0
0 0 0 1
_
_
,
_
_
0 0 0 1
1 0 1 0
0 0 0 0
_
_
,
_
_
0 0 0 0 0
0 0 0 0 0
0 1 0 0 0
0 0 0 0 0
0 0 0 0 0
_
_
.
Teorema 2.9. Toda matriz A M
mn
(K) es equivalente por las a una unica matriz escalonada reducida
por las.
Demostraci on: Si A es la matriz nula, no hay nada que demostrar pues la unica matriz equivalente por
las a A es la propia matriz nula, que es escalonada reducida por las. Supongamos entonces que A es no
nula. La existencia de una matriz escalonada reducida por las que sea equivalente por las a la matriz
A est a garantizada en el comentario 2.10. Veamos ahora la unicidad. Supongamos que G, J M
mn
(K)
son matrices escalonadas reducidas por las tales que A
oef
G y A
oef
J; por tanto existen matrices
invertible E, F M
mm
(K) tales que EA = G y FA = J. Luego existe H M
mm
(K) invertible tal
que HG = J, de hecho H = F
1
E. Por la transitividad de la relaci on
oef
tenemos que G
oef
F.
Note que ambas matrices son, en particular, escalonadas. Consecuentemente, seg un el teorema 2.8, si
j
1
< j
2
< < j
r
y j
1
< j
2
< < j
r
son los ndices de las columnas de E y F, respectivamente, donde
est an los pivotes de estas matrices (recuerde que tales pivotes son iguales a 1), entonces r = r
y para
cada 1 k r se cumple j
k
= j
k
. Por denici on de escalonada reducida por las y la anterior condici on
sobre los ndices j
k
con 1 k r, se tiene:
E
(j
k
)
= F
(j
k
)
= e
(k)
para todo 1 k r; donde e
(k)
es la matriz unicolumna can onica que tienen
el dgito 1 en su entrada k y 0 en las restantes;
para cada j
k
< j < j
k+1
, con 1 k < r; o toda j
k
< j, con k = r, se tiene:
E
(j)
=
_
_
e
1j
.
.
.
e
kj
0
.
.
.
0
_
_
=
k
i=1
e
ij
e
(i)
y F
(j)
=
_
_
f
1j
.
.
.
f
kj
0
.
.
.
0
_
_
=
k
i=1
f
ij
e
(i)
.
En vista de la primera propiedad arriba mencionada, debe mostrarse que E
(j)
= F
(j)
para toda j diferente
de las j
1
, , j
r
. Ahora bien, esta misma condici on y el hecho que HE
(j)
= F
(j)
para toda j, implica en
2.5. Operaciones Elementales por las y Matrices Elementales 33
primer lugar que He
(j)
= e
(j)
para toda j = 1, , r; y en segundo termino lo que deseamos mostrar.
En efecto, usando la segunda de las propiedades antes expuesta se tiene que para toda j diferente de
j
1
, , j
r
vale:
HE
(j)
= H
_
k
i=1
e
ij
e
(i)
_
=
k
i=1
e
ij
He
(i)
=
k
i=1
e
ij
e
(i)
; pero
HE
(j)
= F
(j)
=
k
i=1
f
ij
e
(i)
;
de donde
k
i=1
e
ij
e
(i)
=
k
i=1
f
ij
e
(i)
; es decir, E
(j)
= F
(j)
para toda j diferente de las j
1
, , j
r
.
Ejemplo 2.20. Determinemos la matriz escalonada reducida por las que es equivalente por las a la
matriz A =
_
_
2 2 4 6 4
3 6 3 15 3
5 8 1 17 9
1 1 11 7 7
_
_
. Empleando los procedimientos antes descritos tenemos:
A
f
1
1
2
f
1
_
1 1 2 3 2
3 6 3 15 3
5 8 1 17 9
1 1 11 7 7
_
_
f
2
f
2
+3 f
1
f
3
f
3
5 f
1
f
4
f
4
f
1
_
_
1 1 2 3 2
0 3 9 6 3
0 3 11 2 1
0 2 9 4 5
_
_
f
2
1
3
f
2
_
1 1 2 3 2
0 1 3 2 1
0 3 11 2 1
0 2 9 4 5
_
_
f
1
f
1
+f
2
f
3
f
3
+ 3 f
2
f
4
f
4
2 f
2
_
_
1 0 5 1 3
0 1 3 2 1
0 0 2 4 2
0 0 3 8 3
_
_
f
3
1
2
f
3
_
1 0 5 1 3
0 1 3 2 1
0 0 1 2 1
0 0 3 8 3
_
_
f
1
f
1
5 f
3
f
2
f
2
3 f
3
f
4
f
4
3 f
3
_
_
1 0 0 9 8
0 1 0 8 4
0 0 1 2 1
0 0 0 2 6
_
_
f
4
1
2
f
4
_
1 0 0 9 8
0 1 0 8 4
0 0 1 2 1
0 0 0 1 3
_
_
f
1
f
1
+9 f
4
f
2
f
2
+ 8 f
4
f
3
f
3
2 f
4
_
_
1 0 0 0 35
0 1 0 0 28
0 0 1 0 7
0 0 0 1 3
_
_
.
Con lo cual A tiene rango m aximo (rg(A) = 4); note que la matriz B =
_
_
1 0 0 0 35
0 1 0 0 28
0 0 1 0 7
0 0 0 1 3
_
_
es
escalonada reducida por las, y obviamente equivalente por las a A; por tanto la unica de este tipo
equivalente por las a A.
Corolario 2.4. Para cualquier par de matrices A, B M
mn
(K) se cumple: A
oef
B si, y s olo si, son
equivalentes a la misma matriz escalonada reducida por las.
Demostraci on: (=) Supongamos que A
oef
B. Sean G y F en M
mn
(K) las matrices escalonadas
reducidas por las equivalentes por las a A y B respectivamente. Como A
oef
G y B
oef
F, entonces
34 2.
Algebra Matricial
A
oef
F (por que?). Ahora bien, por la unicidad de las matrices escalonadas reducidas por las
equivalentes por las a una matriz dada, sigue que G = F.
(=) Sigue inmediatamente de la transitividad de la relaci on binaria
oef
.
Comentario 2.12. Interpretemos este corolario en terminos de las nociones de clases de equivalencia
antes recordadas. Si consideramos cualquier matriz A M
mn
(K), entonces toda matriz B en la clase
de equivalencia [A]
oef
tiene la matriz escalonada reducida por las de A. Esto es, podemos seleccionar
las matrices escalonadas reducidas por las como los representantes de las correspondientes clases de
equivalencias inducidas por la relaci on
oef
. As que en adelante a esas matrices escalonadas reducidas
por las las denominaremos formas can onicas de Gauss-Jordan.
Note que:
la forma can onica de cualquier matriz nula es ella misma;
la matriz identidad I
m
, cualquiera sea el natural m, dado que es escalonada reducida por las, es
una de las tantas formas can onicas de Gauss-Jordan en M
mm
(K);
la matriz B obtenida en el ejemplo anterior es la forma can onica de Gauss-Jordan de cualquier
matriz que sea equivalente por las a la matriz A del ejemplo.
2.5.3. Operaciones Elementales por las y Matrices Invertibles
Como recordaremos, cuando se introdujo el concepto de matrices invertibles, o no singulares, comen-
tamos que para abordar el problema de existencia de la inversa de una matriz cuadrada, en caso de que
exista, se requiere de herramientas adicionales a la simple multiplicaci on de matrices. Ac a nos dedica-
remos a conocer una de tales herramientas, de hecho vamos a estudiar la estrecha relaci on que existe
entre las operaciones elementales por las, la forma can onica de Gauss-Jordan de matrices cuadradas, el
problema de decidir si una matriz es invertible o no y el c alculo de su inversa, en caso que sea invertible.
El siguiente resultado establece una caracterizaci on, en terminos de su forma can onica de Gauss-
Jordan, de las matrices invertibles.
Teorema 2.10. Cualquier matriz A M
mm
(K) es invertible si, y s olo si, su forma can onica de Gauss-
Jordan es la matriz identidad I
m
.
Demostraci on: (=) Supongamos inicialmente que A M
mm
(K) es invertible. Mostraremos que su
forma can onica de Gauss-Jordan es I
m
. Por el absurdo, supongamos que esto no es as; es decir, que su
forma can onica de Gauss-Jordan, digamos B M
mm
(K), no es la matriz identidad I
m
. Dado que B
es una matriz cuadrada, si no es la identidad, entonces tiene al menos una la nula (por que?). Como
sabemos, existe una matriz invertible E M
mm
(K), producto de matrices elementales, tal que EA = B;
lo cual en particular implica que B es invertible. Ahora bien, cualquier matriz cuadrada con al menos
una la, o una columna, nula no puede ser invertible (ver ejercicio propuesto 21 en la p agina 40); luego
B no tiene las nulas y en consecuencia es la matriz identidad I
m
.
(=) Recprocamente, supongamos que la forma can onica de Gauss-Jordan de A es I
m
; luego existe E
en M
mm
(K), producto de matrices elementales, tal que EA = I
m
. Dado que E es invertible, sigue que
A = E
1
I
m
= E
1
; por tanto A es invertible; adem as, su inversa A
1
es justamente A
1
= E.
Corolario 2.5. A M
mm
(K) es invertible si, y s olo si, rg(A) = m.
Demostraci on: Se deja al lector.
2.5. Operaciones Elementales por las y Matrices Elementales 35
Determinando inversas de matrices mediante oef
Supongamos que A M
mm
(K) es invertible; por el teorema anterior conocimos no s olo que su forma
can onica de Gauss-Jordan es la identidad I
m
, sino que en la propia demostraci on del teorema se dice
quien es la matriz inversa de A. En efecto, si E = E
k
E
1
, con E
j
(j = 1, , k) elemental, es una
matriz tal que EA = I
m
, entonces A
1
= E = E
k
E
1
I
m
. Esto que signica en terminos pr acticos?
Pues simplemente que al aplicar a I
m
la misma secuencia de oef que se aplican a A para obtener su forma
can onica de Gauss-Jordan, en este caso I
m
, se obtiene la inversa de A.
Esquem aticamente los dos procesos descritos se pueden realizar al mismo tiempo; esto se hace consi-
derando una matriz de orden m2m, en la que del lado izquierdo se coloca la matriz A y del lado derecho
la matriz I
m
; luego se van aplicando oef a esta matriz de orden m 2m siguiendo los procedimientos
para hallar la forma can onica de Gauss-Jordan de A. As, despues de un n umero nito de pasos (cada
uno de ellos denido por una oef) se obtiene en lado izquierdo la forma can onica de Gauss-Jordan de A,
mientras que en lado derecho se obtiene una matriz equivalente por las a la identidad. En el caso que A
sea invertible, en el lado izquierdo tendremos la identidad y en el derecho aparece A
1
.
[A|I
m
]
e
1
[A
1
|E
1
]
e
2
[A
2
|E
2
E
1
]
e
3
e
k1
[A
k1
|E
k1
E
2
E
1
]
e
k
[I
m
|A
1
]. (2.12)
Ejemplo 2.21. Dada la matriz A =
_
_
2 2 4
3 6 3
5 8 1
_
_
; averig uemos si es invertible o no, y en caso de
que lo sea, determinemos su inversa. Procedamos colocando en un mismo arreglo, en este caso de orden
3 6, la matriz A del lado izquierdo y la identidad I
3
en el lado derecho; luego procedemos como lo
descrito arriba.
_
_
2 2 4 1 0 0
3 6 3 0 1 0
5 8 1 0 0 1
_
_
f
1
1
2
f
1
_
_
1 1 2
1
2
0 0
3 6 3 0 1 0
5 8 1 0 0 1
_
_
f
2
f
2
+3 f
1
f
3
f
3
5 f
1
_
_
1 1 2
1
2
0 0
0 3 9
3
2
1 0
0 3 11
5
2
0 1
_
_
f
2
1
3
f
2
_
_
1 1 2
1
2
0 0
0 1 3
1
2
1
3
0
0 3 11
5
2
0 1
_
_
f
1
f
1
+f
2
f
3
f
3
+3 f
2
_
_
1 0 5 1
1
3
0
0 1 3
1
2
1
3
0
0 0 2 1 1 1
_
_
f
3
1
2
f
3
_
_
1 0 5 1
1
3
0
0 1 3
1
2
1
3
0
0 0 1
1
2
1
2
1
2
_
_
f
1
f
1
5 f
3
f
2
f
2
3 f
3
_
_
1 0 0
3
2
17
6
5
2
0 1 0 1
11
6
3
2
0 0 1
1
2
1
2
1
2
_
_
.
Concluimos por tanto que la matriz A es invertible pues su forma can onica de Gauss-Jordan es la identi-
dad; y la matriz que aparece en el lado derecho es la inversa de A; es decir, A
1
=
_
_
3
2
17
6
5
2
1
11
6
3
2
1
2
1
2
1
2
_
_
.
Ejemplo 2.22. Consideremos ahora la matriz A =
_
_
1 2 1
2 1 3
4 5 1
_
_
. Procedamos como antes para ver si
36 2.
Algebra Matricial
A posee inversa, y de ser as calcular tal matriz.
_
_
1 2 1 1 0 0
2 1 3 0 1 0
4 5 1 0 0 1
_
_
f
3
f
3
4 f
1
f
2
f
2
2 f
1
_
_
1 2 1 1 0 0
0 3 5 2 1 0
0 3 5 4 0 1
_
_
f
3
f
3
f
2
_
_
1 2 1 1 0 0
0 3 5 2 1 0
0 0 0 2 1 1
_
_
.
Dado que en el lado izquierdo del arreglo ampliado ya se tiene una forma escalonada equivalente por las
a A y tal matriz escalonada tiene una la nula, entonces A no es invertible pues rg(A) = 2 < 3. Puede,
obviamente, continuarse el proceso de obtenci on de la forma can onica de Gauss-Jordan de A (ya no se
requiere la parte de la derecha); de hecho:
_
_
1 2 1
0 3 5
0 0 0
_
_
f
2
1
3
f
2
_
_
1 2 1
0 1
5
3
0 0 0
_
_
f
1
f
1
2 f
2
_
_
1 0
7
3
0 1
5
3
0 0 0
_
_
.
Por tanto la forma can onica de Gauss-Jordan de A es B =
_
_
1 0
7
3
0 1
5
3
0 0 0
_
_
.
Comentario 2.13. Haciendo uso de la forma can onica de Gauss-Jordan hemos visto que si para A en
M
mm
(K) existe B M
mm
(K) invertible tal que BA = I
m
, entonces A es invertible y A
1
= B; esto
es, para vericar que A sea invertible basta con hallar una matriz invertible B que multiplicada a la
izquierda de A resulte la identidad. Como recordaremos, la denici on de invertibilidad de matrices es
m as especca, ver p agina 19, se requiere de una matriz B M
mm
(K) tal que AB = BA = I
m
para
que A sea invertible, y en tal caso A
1
= B. Surge por tanto la siguiente interrogante: se podr a concluir
la invertibilidad de A si existe B M
mm
(K) de forma que AB = I
m
o BA = I
m
?
Consideremos que BA = I
m
; si B M
mm
(K) es invertible, entonces por lo anterior A es invertible.
Supongamos que B no es invertible. Sea J M
mm
(K) la forma can onica de Gauss-Jordan de B.
Note que J tiene al menos una la nula, pues B es no invertible. Luego existe E M
mm
(K) invertible
(producto de matrices elementales) tales que EB = J. Dado que BA = I
m
, tenemos:
E(BA) = EI
m
= E y E(BA) = (EB)A = JA;
as que E = JA. Recuerde que E es invertible y J tiene al menos una la nula. Esto es una contradicci on!,
vea nuevamente el ejercicio propuesto 21 en la p agina 40. Concluimos de esta forma que si BA = I
m
, con
A, B M
mm
(K), entonces A es invertible y A
1
= B. Con los mismos argumentos se muestra que si
AB = I
m
, con A, B M
mm
(K), entonces A es invertible y A
1
= B.
Cu al es la moraleja de esta corta historia? Pues que no hace falta vericar tanto AB = I
m
como
BA = I
m
, con B M
mm
(K), para armar que A es invertible y que A
1
= B; basta con tener una de
esas condiciones satisfechas para que A sea invertible y su inversa igual a B; es m as, se puede demostrar
que: una de las condiciones anteriores se satisface si, y s olo si, la otra condici on de la denici on de
invertibilidad tambien se cumple; se deja la vericaci on al lector
2.6. Ejercicios Propuestos 37
2.6. Ejercicios Propuestos
1. Clasique cada una de las matrices dadas, seg un sean: triangular superior, triangular inferior,
diagonal, escalar, simetrica o antisimetrica:
a)
_
_
2 0 1
0 1 1
0 0 0
_
_
b)
_
_
1 0 0
0 1 0
0 0 1
_
_
c)
_
_
1 0 1
0 1 1
1 1 0
_
_
d)
_
_
1 0 0
0 2 0
0 0 3
_
_
e)
_
_
2 0 0
0 2 0
0 0 2
_
_
f)
_
_
2 0 1
0 1 1
0 0 0
_
_
g)
_
_
0 0 1
0 0 2
1 2 0
_
_
h)
_
_
1 1 1
1 1 2
1 2 1
_
_
i)
_
_
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
_
_
d)
_
_
0 0 1
0 1 0
1 0 0
_
_
2. Determine la matriz traspuesta de cada una de las matrices que se listan a continuaci on.
a)
_
_
2 0 1
0 1 1
0 0 0
_
_
b)
_
_
0 0 1 2
0 1 0 1
1 0 0 2
_
_
c)
_
_
0 0 1
0 0 2
1 2 0
_
_
d)
_
_
1 0 0
1 2 0
2 2 3
_
_
e)
_
_
2 0 0
1 2 0
1 0 2
_
_
3. Dadas las matrices
A =
_
_
2 1 i
3 0 1 i
0 1 2 i
_
_
, B =
_
_
1 2 0
i 2i 0
4 1 3
_
_
, C =
_
_
2 1 3
0 2 5
2 0 3
_
_
,
D =
_
_
1 +i i 2 0
i 1 i 3 1
0 1 2 1 +i
_
_
, y E =
_
_
1 2 3 4
2 3 4 1
3 4 1 2
_
_
.
Realizar cada una de las siguientes operaciones:
a) A+ 2B b) A
2
B + 3B
2
c) (A+B)
2
d) AB +AC
t
e) CB BC
f) CD 2E g) 2D
t
A3E
t
h) A(B 2C
2
) b)
1
2
(C +C
t
) c)
1
2
(C C
t
)
4. Una empresa de productos qumicos produce dos reactivos A y B en dos laboratorios X e Y. Durante
la fabricaci on de los reactivos de producen tres agentes contaminantes: a,b y c. Por cada kilogramo
de cada reactivo producido se generan ciertas cantidades, en kilogramos, de tales contaminantes que
se expresan mediante la matriz C =
_
a b c
A 0,05 0,02 0,12
B 0,08 0,1 0,025
_
. Dado que es necesario la eliminaci on
de tales contaminantes, la empresa invierte, por kilogramo de cada contaminante, cierta cantidad
en bolvares que se expresa para cada laboratorio mediante D =
_
_
X Y
a 1250 540
b 850 1000
c 250 1010
_
_
. Interprete
cada una de las entradas de la matriz CD.
38 2.
Algebra Matricial
5. La producci on de un kilogramo de los alimentos P y Q requiere de cierta cantidad, en gra-
mos, de tres conservantes: a, b y c. Los valores de estas cantidas se almacenan en la matriz
A =
_
a b c
P 25 20 15
Q 100 10 25
_
. Ahora bien, la ingesta de cada gramo de los respectivos conservantes
produce en el organismo cierta cantidad, medida en microgramos, de los agentes cancerigenos v y
w; estas cantidades se expresan por B =
_
_
v w
a 150 100
b 50 70
c 200 10
_
_
. Interprete cada una de las entradas de
la matriz AB.
6. Demostrar que cualquier matriz A =
_
a b
c d
_
es combinaci on lineal de las matrices can onicas:
E
11
=
_
1 0
0 0
_
, E
2
=
_
1 1
0 0
_
, E
3
=
_
1 1
1 0
_
y E
2
=
_
1 1
1 1
_
. Generalizar esta propiedad en M
mn
(K).
7. Sea A =
_
_
0 0 0
1 0 0
0 1 0
_
_
. Demostrar que A
2
=
_
_
0 0 0
0 0 0
1 0 0
_
_
y A
3
= O. Generalizar para A de orden
mm.
8. Una matriz A de orden mm se dice nilpotente de orden k 1 si A
k
= O y A
k1
= O.
Decidir cu ales de las siguientes matrices son nilpotentes:
_
_
1 1 0
1 1 0
2 2 0
_
_
,
_
_
0 5 10
0 1 2
0 3 6
_
_
,
_
_
6 0 1
2 3 2
1 3 1
_
_
y
_
_
0 1 0 0
0 0 1 0
0 0 0 1
0 0 0 0
_
_
.
Demostrar que si A es nilpotente de orden 2, entonces I
m
A es invertible y su inversa es I
m
+A.
9. Una matriz A de orden mm se dice ortogonal si AA
t
= A
t
A = I
m
, donde A
t
es la traspuesta de
A.
Decidir cu ales de las siguientes matrices son ortogonales:
_
_
1 1 0
1 1 0
2 2 0
_
_
,
_
_
1 0 0
0 0 1
0 1 0
_
_
,
_
_
1 0 0
0
1
2
1
2
0
1
2
1
2
_
_ y
_
cos sen
sen cos
_
, con R.
Demostrar que A M
mm
(K) es ortogonal si, y s olo A es invertible y A
1
= A
t
.
10. Para R, sea A
=
_
cos sen
sen cos
_
. Demostrar que para cualquier entero positivo k se cumple
que A
k
=
_
cos k sen k
sen k cos k
_
.
11. Dos matrices A, B M
mm
(K) se dice que conmutan si AB = BA.
a) Determine todas las matrices B M
22
(K) que conmutan con A =
_
1 2
2 1
_
.
2.6. Ejercicios Propuestos 39
b) Que matrices conmutan con una matriz diagonal?
c) Dadas A, B M
mm
(K), ambas simetricas. Demostrar que AB es simetrica si, y s olo si,
AB = BA.
d) Demostrar que A M
22
(K) conmuta con cualquier matriz B M
22
(K) si, y s olo si, A
conmuta con cada una de las matrices can onicas. Es cierto en general?; esto es, vale tal
propiedad para A M
mm
(K) cualquiera sea m 2?
12. Dada cualquier matriz A M
mm
(K). Demostrar que B =
1
2
(A+A
t
) es simetrica y C =
1
2
(AA
t
)
es antisimetrica. Deducir que toda matriz cuadrada se expresa como la suma de una matriz simetrica
y una antisimetrica.
13. Completar la demostraciones de: proposici on 2.1, teorema 2.1, proposici on 2.2 y teorema 2.2..
14. Demostrar que cualesquiera sean los enteros k, 2, los escalares
1
, ,
k
K y las matrices
A
1
, , A
M
mn
(K), se cumple:
_
_
k
j=1
j
_
_
_
i=1
A
i
_
=
k
j=1
i=1
(
j
A
i
) =
i=1
k
j=1
(
j
A
i
).
15. Dadas matrices A, B M
mm
(K), demostrar que (A+B)
2
= A
2
+ 2AB +B
2
si, y s olo si, A y B
conmutan.
16. Decidir acerca de la veracidad o falsedad de cada una de las siguientes proposiciones. Justique
razonadamente su respuesta; esto es, ofrezca una demostraci on si la proposici on es verdadera, o un
contraejemplo en caso que sea falsa.
a) La suma de matrices triangulares es triangular.
b) La suma y el producto de matrices triangulares superiores (resp. inferiores) es triangular su-
perior (resp. inferior).
c) Si A y B son matrices triangulares superiores (resp. inferiores, diagonales, escalares, simetricas
o antisimetricas) del mismo orden, y es un escalar, entonces A + B es tambien triangular
superior (resp. inferior, diagonal, escalar, simetrica o antisimetrica).
d) Siempre tiene sentido calcular potencias enteras de cualquier matriz.
e) Si A M
mn
(K) y B M
nk
(K) son tales que AB es la matriz nula de orden mk, entonces
alguna de las matrices A, B es nula.
f ) Si A M
mm
(K) es tal que AA
t
= O, entonces A = O.
g) Toda matriz cuadrada no nula es invertible.
h) Para todo par de matrices cuadradas del mismo orden A y B se cumple AB = BA.
i ) Si A es una matriz cuadrada, entonces para todo par de enteros positivos k, se cumplen
A
k
A
= A
A
k
= A
k+
.
j ) Si A, B M
mm
(K), entonces (A+B)
2
= A
2
+AB +BA+B
2
.
k) Si A y B son matrices cuadradas invertibles del mismo orden, entonces A+B tambien lo es.
l ) Si A y B son del mismo orden las cuales son equivalentes por las, y si C y D son matrices
escalonadas equivalentes por las a A y B, respectivamente, entonces C = D.
40 2.
Algebra Matricial
m) Si A y B son del mismo orden las cuales son equivalentes por las, entonces tienen el mismo
rango.
n) Si A es una matriz cuadrada cuya forma can onica de Gauss-Jordan tiene una la nula, entonces
A es invertible.
n) Si A M
mm
(K) tiene rango k < m, entonces A no es invertible.
17. Sea = 0. Demostrar que para todo entero positivo n vale la identidad:
_
cos sen
1
k
sen cos
_n
=
_
cos(n) sen(n)
1
k
sen(n) cos(n)
_
.
18. Completar la demostraci on del teorema 2.3.
19. Sean A =
_
a b
c d
_
. Demostrar que A es invertible si, y s olo si ad cb = 0. En tal caso, vericar
que la inversa de A es A
1
=
1
adbc
_
d b
c a
_
. Empleando este criterio, cu ales de las siguientes
matrices son invertible?
_
1 2
1 1
_
,
_
a b
b a
_
y
_
1 1
1 1
_
.
20. Para cualquier entero k 2 vale: si A
1
, A
2
, , A
k
son matrices invertibles de M
mm
(K), entonces
el producto A
1
A
2
A
k
es invertible y (A
1
A
2
A
k
)
1
= A
1
k
A
1
k1
A
1
1
.
Sea A M
mm
(K). Demostrar que A es invertible si, y s olo si, para cada entero positivo k, A
k
es
invertible; en tal caso
_
A
k
_
1
= A
k
= A
1
A
1
. .
k veces
.
Sean A, B M
mm
(K) tales que AB es invertible. Demostrar que tanto A como B son invertibles.
Generalize tal propiedad para un n umero nito de matrices. Compare con la primera parte de este
ejercicio.
21. Sea A M
mm
(K). Demostrar que:
a) si la la i de A, A
(i)
, es nula, entonces para cualquier matriz B M
mp
(K), la la i de la
matriz producto AB tambien es nula.
b) si la columna j de A, A
(j)
, es nula, entonces para cualquier matriz B M
pm
(K), la columna
j de BA tambien es nula.
Deducir que cualquier matriz cuadrada con al menos una la, o una columna, nula no es invertible.
22. Sean A, B M
mm
(K) invertibles tales que A + B tambien lo es. Demostrar que A
1
+ B
1
es
tambien invertible, y adem as (A
1
+B
1
)
1
= A(A+B)
1
B = B(A+B)
1
A.
23. Completar la demostraci on del teorema 2.6.
24. Demostrar que el rango de cualquier matriz de orden mn es siempre menor o igual al mn{m, n}.
25. Demostrar el corolario 2.5.
2.6. Ejercicios Propuestos 41
26. Para cada una de las matrices se listan a continuaci on determine su rango y forma can onica de
Gauss-Jordan.
_
1 2 1 4
,
_
_
0
2
5
2
_
_
,
_
1 2 1 4
2 3 1 2
_
,
_
_
2 1 7 10
1 1 8 14
3 4 3 0
_
_
y
_
_
2 1 2 0
1 1 1 2
3 2 3 2
2 1 0 1
2 4 5 3
_
_
.
27. Empleando operaciones elementales por las, determine cu ales de las siguientes matrices es inver-
tible; para aquellas que lo sean, encontrar su inversa.
_
2 2
1 4
_
,
_
2 1
8 4
_
,
_
a b
b a
_
, (a = 0),
_
_
2 2 1
4 2 0
2 1 0
_
_
,
_
_
2 0 1
4 0 0
2 1 0
_
_
,
_
_
5 5 1
1 1 1
0 2 3
_
_
,
_
_
5 2 3
1 2 3
1 2 1
_
_
,
_
_
i 2 1 +i
i 3i 1
i 4 + 6i 1 2i
_
_
,
_
_
1 i 2 i
1 0 1 +i
1 +i 2 2 +i
_
_
,
_
_
1 1 1 1
1 3 1 2
5 9 1 6
1 2 1 1
_
_
,
_
_
2 0 1 5
1 3 3 2
1 2 3 1
3 1 2 5
_
_
y
_
_
2 0 1 2 1 0
1 2 1 1 2 2
1 0 1 1 2 1
1 2 1 3 1 2
0 1 2 1 2 1
2 1 2 1 0 0
_
_
.
28. Determine los valores de R, si es que existen, de manera que la matriz A =
_
_
1 2
1 0 0
1 1 1
_
_
sea
invertible. Determine su inversa en tales casos.
29. Sean A M
mm
(K) y A
(1)
, , A
(m)
las las de A. Demostrar que si una de tales las se escribe
como la suma de m ultiplos de las restantes las, entonces A es no invertible. Es cierto el recproco?
Sugerencia: Demuestre que bajo tal hip otesis la forma can onica de Gauss-Jordan de A tiene al menos una la nula
30. Dada A = [a
ij
] M
mn
(C), se dene la traspuesta hermitiana de A como la matriz A
= [b
ij
] de
M
nm
(C) tal que b
ij
= a
ji
para todo i = 1, , n y cada j = 1, , m.
a) Determine A
para cada una de las matrices dadas.
_
1 1 i
2 i 0
_
,
_
1 2
3 4
_
,
_
1 +i i 2
2 +i 3 2i 2
_
y
_
_
1 +i 0
2 +i 1 + 2i
2 i
_
_
.
b) Demostrar cada una de las siguientes armaciones:
1) A, B M
mn
(C): (AB)
= A B
.
2) A M
mn
(C) y B M
np
(C): (AB)
= B
.
3) C y A M
mn
(C): (A)
= A
.
4) A M
mn
(C): (A
= A.
42 2.
Algebra Matricial
c) Una matriz A = [a
ij
] M
mm
(C) se dice: hermitiana si A
= A; y es antihermitiana si
A
= A. Demostrar:
1) Si A es hermitiana, entonces a
ii
R para todo i = 1, , m. Es cierto el recproco?
2) Si A es antihermitiana, entonces a
ii
/ R para todo i = 1, , m. Es cierto el recproco?
3) Si A es diagonal y hermitiana, entonces todas las entradas de A son n umeros reales.
Que puede decir si A es diagonal y antihermitiana?
4) Si A es hermitiana, entonces existen matrices A
1
y A
2
con todas sus entradas en R tales
que: A
1
es simetrica, A
2
es antisimetrica y A = A
1
+iA
2
.
31. Al igual que las operaciones elementales por la, se introducen las operaciones elementales por
columnas y matrices elementales por columnas:
Tipo I: multiplicar una columna por un escalar no nulo: c
j
c
j
;
Tipo II: sustituir una columna por ella m as un m ultiplo de otra: c
j
c
j
+c
i
; y
Tipo III: intercambiar dos columnas: c
j
c
i
.
Una matriz cuadrada se dice elemental por columna si es obtenida de la identidad mediante
la aplicaci on de una unica operaci on elemental por columnas.
Se propone al lector desarrollar una teora paralela a la de operaciones elementales por las, ma-
trices elementales, rango la, formas escalonadas, formas can onicas de Gauss-Jordan y la relaci on
con matrices invertibles, pero ahora empleando operaciones elementales por columna y matrices
elementales por columnas.
32. Toda matriz A M
mn
(K) se puede expresar como una matriz por bloques; esto se obtiene trazando
uno o m as segmentos horizontales y verticales atravesando el arreglo A; los subarreglos denidos
por los sectores obtenidos mediante tales segmentos se les conoce como bloques de A, o tambien
como submatrices de A. La matriz A =
_
_
1 2 9 0
2 1 0 0
0 0 0 0
_
_
puede expresarse de diferentes manera como
una matriz por bloques; por ejemplo:
a)
_
A
1
A
2
A
3
A
4
_
, donde A
1
=
_
1 2
2 1
_
, A
2
=
_
9 0
0 0
_
, A
3
= A
4
=
_
0 0
;
b)
_
A
1
A
2
A
3
A
4
_
, donde A
1
=
_
1 2 9
2 1 0
_
, A
2
=
_
0
0
_
, A
3
=
_
0 0
y A
4
=
_
0
; o tambien como
c)
_
A
1
A
2
_
, donde A
1
=
_
1 2 9 0
y A
2
=
_
2 1 0 0
0 0 0 0
_
; o incluso con A
1
=
_
1 2 9 0
2 1 0 0
_
y A
2
=
_
0 0 0 0
.
i). Sean A, B M
mn
(K) las cuales han sido separadas por bloques de la misma manera:
A =
_
_
A
11
A
12
A
1k
A
21
A
22
A
2k
.
.
.
.
.
.
.
.
.
A
p1
A
p2
A
pk
_
_
y B =
_
_
B
11
B
12
B
1k
B
21
B
22
B
2k
.
.
.
.
.
.
.
.
.
B
p1
B
p2
B
pk
_
_
.
2.6. Ejercicios Propuestos 43
Demostrar que
A+B =
_
_
A
11
+B
11
A
12
+B
12
A
1k
+B
1k
A
21
+B
21
A
22
+B
22
A
2k
+B
2k
.
.
.
.
.
.
.
.
.
A
p1
+B
p1
A
p2
+B
p2
A
pk
+B
pk
_
_
, y A =
_
_
A
11
A
12
A
1k
A
21
A
22
A
2k
.
.
.
.
.
.
.
.
.
A
p1
A
p2
A
pk
_
_
.
ii). Sean A M
mn
(K) y B M
n
(K) que descompuestas en bloques:
A =
_
_
A
11
A
12
A
1k
A
21
A
22
A
2k
.
.
.
.
.
.
.
.
.
A
p1
A
p2
A
pk
_
_
y B =
_
_
B
11
B
12
B
1s
B
21
B
22
B
2s
.
.
.
.
.
.
.
.
.
B
k1
B
k2
B
ks
_
_
de manera que tenga sentido la operaci on A
it
B
tj
para todo 1 i p, 1 t k y 1 j s.
Demostrar que
AB =
_
_
C
11
C
12
C
1s
C
21
C
22
C
2s
.
.
.
.
.
.
.
.
.
C
p1
C
p2
C
pk
_
_
donde C
ij
=
k
t=1
A
it
B
tj
.
iii). Una matriz cuadrada A de orden m m se dice diagonal por bloques si se escribe da la
forma A =
_
_
A
1
A
2
O
.
.
.
O A
k1
A
k
_
_
, donde las matrices A
j
(j = 1, , k) son cuadradas, no
necesariamente del mismo orden, pero cuya de ordenes es m; y fuera de la diagonal los restantes
bloques son matrices nulas. Demostrar:
a) Para cada entero positivo s se cumple A
s
=
_
_
A
s
1
A
s
2
O
.
.
.
O A
s
k1
A
s
k
_
_
.
b) Si B =
_
_
B
1
B
2
O
.
.
.
O B
k1
B
k
_
_
es otra matriz diagonal por bloques y descompuesta de
la misma forma que A, entonces AB =
_
_
A
1
B
1
A
2
B
2
O
.
.
.
O A
k1
B
k1
A
k
B
k
_
_
. Demues-
44 2.
Algebra Matricial
tre tambien que A es invertible si, y s olo si cada matriz A
j
(j = 1, , k) es invertible, y en
tal caso A
1
=
_
_
A
1
1
A
1
2
O
.
.
.
O A
1
k1
A
1
k
_
_
.
33. Sea A =
_
_
A
1
A
2
O
.
.
.
O A
k1
A
k
_
_
una matriz diagonal por bloques. Demostrar que la forma
can onica de Gauss-Jordan de Aes tambien diagonal por bloques B =
_
_
B
1
B
2
O
.
.
.
O B
k1
B
k
_
_
,
donde cada bloque B
j
en la diagonal de B es la forma can onica de Gauss-Jordan de A
j
. Deducir
que el rango de A es la suma de los rangos de las matrices bloques de la diagonal. Proporcione
ejemplos de tales matrices.
34. Dar un concepto de cuando una matriz cuadrada est a en la forma triangular superior (resp. inferior)
por bloques. Expresar la forma can onica de Gauss-Jordan de una tal matriz en terminos de las
formas can onicas de Gauss-Jordan de las matriz bloques de la diagonal de la matriz triangular
superior por bloques. Proporciones ejemplos de tales tipos de matrices.
35. Dada A M
mn
(K), se dice que A es invertible por la izquierda, si existe L M
nm
(K) tal que
LA = I
n
; y es invertible por la derecha, si existe R M
nm
(K) tal que AR = I
m
. Las matrices L
y R se conocen como inversas laterales de A, por la izquierda y la derecha respectivamente.
a) Determine, en caso de existir, inversas laterales de la matriz A = [1 0 1].
b) Mediante ejemplos vericar que las inversas laterales pueden no ser unicas; de hecho pueden
existir innitas matrices que son inversas por un mismo lado.
c) Demostrar que si A es cuadrada, entonces A es invertible, seg un la denici on 2.14, si, y s olo
si, es invertible tanto por la derecha como por la izquierda; en tal caso las inversas laterales
coinciden con la inversa de A.
d) Puede una matriz cuadrada ser invertible por un lado y no por el otro?
e) Construya ejemplos de matrices que tengan inversa por un lado, pero no sea invertible por el
otro lado.
Vous aimerez peut-être aussi
- Diagrama de Mollier SolkaneDocument11 pagesDiagrama de Mollier SolkaneCesar Orlando Barria VeraPas encore d'évaluation
- Biblioteca Camara 2016 12 001 PDFDocument45 pagesBiblioteca Camara 2016 12 001 PDFmauricioPas encore d'évaluation
- REFRIGERACIONDocument128 pagesREFRIGERACIONRoger ParraPas encore d'évaluation
- GIZ Tutorial Refrigeración 2015Document144 pagesGIZ Tutorial Refrigeración 2015Roger ParraPas encore d'évaluation
- Biblioteca Camara 2016 12 001 PDFDocument45 pagesBiblioteca Camara 2016 12 001 PDFmauricioPas encore d'évaluation
- Diseño y Calculos Aislamiento AISLAM GT3 - 07 (IDAE)Document64 pagesDiseño y Calculos Aislamiento AISLAM GT3 - 07 (IDAE)El3ctrikPas encore d'évaluation
- Manual de Aplicaciones - DANFOSSDocument152 pagesManual de Aplicaciones - DANFOSSMarquiño Riveros Geronimo100% (3)
- 9110 - David Solis Ansi 2 Iiar-Ciemi - RevDocument47 pages9110 - David Solis Ansi 2 Iiar-Ciemi - RevRoger Ramos100% (1)
- Tanque Y&v 13 (Chaq - Aislante)Document2 pagesTanque Y&v 13 (Chaq - Aislante)Roger ParraPas encore d'évaluation
- DiorcaDocument89 pagesDiorcaRoger ParraPas encore d'évaluation
- Presentación DomoDocument32 pagesPresentación DomoRoger ParraPas encore d'évaluation
- Fallas en PinturaDocument18 pagesFallas en PinturaRoger ParraPas encore d'évaluation
- Fallas en PinturaDocument31 pagesFallas en Pinturaleunam26100% (2)
- Ir-S-06 Manejo Del CambioDocument24 pagesIr-S-06 Manejo Del CambioIllargi Uzcanga Meabe25% (4)
- Si-S-04 - (2015) Requisitos SihoDocument68 pagesSi-S-04 - (2015) Requisitos SihoMarielys Hernandez92% (12)
- Tanque Y&V 13 (I)Document3 pagesTanque Y&V 13 (I)Roger ParraPas encore d'évaluation
- Presentacion Producto 12 (I)Document4 pagesPresentacion Producto 12 (I)Roger ParraPas encore d'évaluation
- Tanque Y&v 13 Tuberia InoxidableDocument3 pagesTanque Y&v 13 Tuberia InoxidableRoger ParraPas encore d'évaluation
- Tabla Equivalecia PDVSA O-201 - Agost 11Document2 pagesTabla Equivalecia PDVSA O-201 - Agost 11Roger ParraPas encore d'évaluation
- Tanque San Felipe 13 (II)Document7 pagesTanque San Felipe 13 (II)Roger ParraPas encore d'évaluation
- Tanque Y&v 13 Sustrato FerrosoDocument6 pagesTanque Y&v 13 Sustrato FerrosoRoger ParraPas encore d'évaluation
- Presentacion Sikarustex (II) 13Document15 pagesPresentacion Sikarustex (II) 13Roger ParraPas encore d'évaluation
- Sanblasol - 10-4-12Document4 pagesSanblasol - 10-4-12Roger ParraPas encore d'évaluation
- Presentacion Sikarustex (II) 13Document15 pagesPresentacion Sikarustex (II) 13Roger ParraPas encore d'évaluation
- Inver. Delran - 05-06-12Document6 pagesInver. Delran - 05-06-12Roger ParraPas encore d'évaluation
- Recub. Galvanizado (X) 13Document5 pagesRecub. Galvanizado (X) 13Roger ParraPas encore d'évaluation
- HCL-Melonws (08-03-13) IIDocument4 pagesHCL-Melonws (08-03-13) IIRoger ParraPas encore d'évaluation
- Epoxifenolico S400 13Document17 pagesEpoxifenolico S400 13Roger ParraPas encore d'évaluation
- HCL - 12-7-12Document9 pagesHCL - 12-7-12Roger ParraPas encore d'évaluation
- Respeto A La Dignidad HumanaDocument11 pagesRespeto A La Dignidad HumanaSámely Durán Antezana100% (1)
- Medidores de Vibracion SegundoDocument11 pagesMedidores de Vibracion SegundoYinis Andreiita Acevedo100% (1)
- Informes de Actividad de PromocionDocument38 pagesInformes de Actividad de PromocionDelia Ma PCPas encore d'évaluation
- TR-01 Protocolo de Trazo y Replanteo de Tuberia AciDocument1 pageTR-01 Protocolo de Trazo y Replanteo de Tuberia AciJonatan ParedesPas encore d'évaluation
- Modelado Sistémico Y Simulación (SI 701) : Docente: Anival Torre CamonesDocument97 pagesModelado Sistémico Y Simulación (SI 701) : Docente: Anival Torre CamonesNILO ISRAEL PEÑA TASAYCOPas encore d'évaluation
- Oficio SterenDocument1 pageOficio SterenivanabeltrancarreonPas encore d'évaluation
- El huevo de obsidiana: efectos energéticos y terapéuticosDocument10 pagesEl huevo de obsidiana: efectos energéticos y terapéuticosLupita CuevasPas encore d'évaluation
- Práctica 03 (Preparación)Document11 pagesPráctica 03 (Preparación)John QueralesPas encore d'évaluation
- Control de bombeo con variador de velocidadDocument7 pagesControl de bombeo con variador de velocidadJosé FlzPas encore d'évaluation
- 06 de Junio de 2021Document56 pages06 de Junio de 2021Efra GonzalezPas encore d'évaluation
- Redes DefDocument78 pagesRedes DefJose F. ZapataPas encore d'évaluation
- Contracción Muscular-Impulso NerviosoDocument3 pagesContracción Muscular-Impulso NerviosoRosanaLunaVillanuevaPas encore d'évaluation
- Actividades de Enfermería en La Visita DomiciliariaDocument4 pagesActividades de Enfermería en La Visita Domiciliariamaria valentina segoviaPas encore d'évaluation
- sm3 Geometria2Document35 pagessm3 Geometria2Gustavo AraratPas encore d'évaluation
- Producto - Com 6º - Sva 09Document6 pagesProducto - Com 6º - Sva 09Mateo OrvarPas encore d'évaluation
- Ensamble y DesensambleDocument8 pagesEnsamble y DesensambleKristian BarriosPas encore d'évaluation
- Manual Motoniveladora 2020Document123 pagesManual Motoniveladora 2020Alumnos Teóricos67% (3)
- 7 Decisiones (El Regalo Del Viajero)Document8 pages7 Decisiones (El Regalo Del Viajero)AlejandroB.CoaguilaPas encore d'évaluation
- Em Botella DoDocument20 pagesEm Botella DoOliver RomeroPas encore d'évaluation
- SILVERADO InmovilizadorDocument67 pagesSILVERADO InmovilizadorClaudio BravoPas encore d'évaluation
- Villoro. Filosofía para Un Fin de Época. CitasDocument3 pagesVilloro. Filosofía para Un Fin de Época. CitasoliverioPas encore d'évaluation
- Dieta equilibrada para Hermes y JoséDocument6 pagesDieta equilibrada para Hermes y JoséPiero CorimanyaPas encore d'évaluation
- Nuestra Cocina - Cocina VascaDocument108 pagesNuestra Cocina - Cocina VascaMariano GómezPas encore d'évaluation
- Semana 06 - Agregados para La Construccion 02Document45 pagesSemana 06 - Agregados para La Construccion 02GROVER ESPINOZA MONARESPas encore d'évaluation
- El Sabor de La NostalgiaDocument35 pagesEl Sabor de La NostalgiaJose RodriguezPas encore d'évaluation
- Ejercicios para ExamenDocument2 pagesEjercicios para Examenmiguel felix felixPas encore d'évaluation
- FactorialDocument3 pagesFactorialRonald HerreraPas encore d'évaluation
- Advanced Pragmatic Psychology - Gary M. Douglas Susanna Mittermaier - Z LibraryDocument111 pagesAdvanced Pragmatic Psychology - Gary M. Douglas Susanna Mittermaier - Z Librarynicolas.chainPas encore d'évaluation
- Normas de seguridad para ayudantes de grúa optimizan la seguridadDocument15 pagesNormas de seguridad para ayudantes de grúa optimizan la seguridadLeiva Gonzales S. PatriciaPas encore d'évaluation
- El Camino de Jesús en 47 fotosDocument165 pagesEl Camino de Jesús en 47 fotosJAndresPuertaLopezPas encore d'évaluation