Académique Documents
Professionnel Documents
Culture Documents
Supercapacitor Model
Transféré par
Leng SovannarithDescription originale:
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Supercapacitor Model
Transféré par
Leng SovannarithDroits d'auteur :
Formats disponibles
SIITME2009 15th International Symposium for Design and Technology of Electronics Packages
Modeling and Simulation of Supercapacitors
C. Frca, D. Petreu, I. Ciocan and N. Palaghi
Department of Applied Electronics, Faculty of Electronics, Telecommunications and Information Technology, Technical University of Cluj-Napoca, Cluj-Napoca, Romania Email: Cristian.Farcas@ael.utcluj.ro
Abstract: In this paper we present some models for supercapacitors. The supercapacitors are used more and more in high level industries such as: traction systems, automotive industry, aerospace industry, telecommunications etc. Undestanding supercapacitors operation mode is necessary so we can be able to determine the applications which require these components, and to be able to choose between supercapacitors and other energy storage devices. In this paper were used some models for the implementation of supercapacitors, and the simulations made in Orcad 9.2 to determine their operation, are in time and frequency domain. Also, the models were implemented in Simulink 7.5 and the simulation results prove the models accuracy. Two test measurements on the ECOND Pscap350 supercapacitor were realized and using the measurement data, two methods to compute the parameters are presented.
high peak power due to their internal equivalent series resistance (ESR). The ultracapacitors, also known as supercapacitors, solves many of the limitations that arise with batteries. The biggest downside to ultracapacitors is that though they have a larger power density than batteries, they also have a smaller energy density than batteries. This means that for a capacitor and battery of equal volume, the battery can potentially store more energy than the capacitor, but the capacitor can output stored energy as power at a faster rate compared to the battery [1]. The supercapacitor resembles a regular capacitor with the exception that it offers very high capacitance in a small package. Energy storage is by means of static charge rather than of an electro-chemical process that is inherent to the battery. Applying a voltage differential on the positive and negative plates charges the supercapacitor [2]. The supercapacitor can be recharged and discharged virtually an unlimited number of times. Unlike the electrochemical battery, there is very little wear and tear induced by cycling and age does not affect the supercapacitor much. In normal use, a
195 17-20 Sep 2009, Gyula, Hungary
1. INTRODUCTION
Electrical energy can be stored in two different ways: indirectly in batteries as potentially available chemical energy requiring faradic oxidation and reduction of the electro-active agents to release charges that can perform electrical work when they flow between two electrodes having different electrode potentials, and directly in an electrostatic way as negative and positive electric charges on the plates of a capacitor by a process termed as non-faradic electrical energy storage.
Batteries have several downsides that eliminate their use as the primary power storage source. They recharge slowly, have a limited number of recharge cycles, require large volumes of space and weight, have a cold intolerance, and while batteries have a high energy density they also have a very low power density which means they are good for constant low power devices, but cannot produce short bursts of
978-1-4244-50330309/$26.00 2009 IEEE
SIITME2009 15th International Symposium for Design and Technology of Electronics Packages
supercapacitor deteriorates to about 80 percent after 10 years. The self-discharge of the supercapacitor is substantially higher than that of the electro-chemical battery. Supercapacitors with an organic electrolyte are affected the most. In 30 to 40 days, the capacity decreases from full charge to 50 percent. In comparison, a nickel-based battery discharges about 10 percent during that time [3].
battery. And they can deliver all their stored energy virtually instantaneously within a few thousandths of a second. In energy storage by a capacitor, only an excess and a deficiency of electron charges on the capacitor plates have to be established on charge and the reverse on discharge and no chemical changes are involved. Accordingly, a capacitor has an almost unlimited recyclability, typically between 105 and 106 times. As a result, capacitors have a substantially low energy-density. When comparing supercapacitors with batteries the main difference is in energy and power density. A supercapacitor has a higher power density than a battery, but it has a significantly lower energy density than a battery, as in figure 2 [4].
103 102 10 Supercapacitors 1 10-1 Capacitors 10-2 1 10 102 Specific power [W/kg] 103 104
2. SUPERCAPACITORS VERSUS BATTERY
A storage battery has two different types of active materials entrapped in a suitably conductive matrix as anodes and cathodes to sustain the net cell reactions, while a capacitor comprises a dielectric sandwiched between two identical electrodes (figure 1).
Charge +Q Dielectric -Q
S pecific energy [W h/kg ]
Lead Acid, NiCd, LiIon Batteries
Electric field E
Fig. 1. Conventional capacitor.
Fig. 2. Ragone plot of various energy storage devices.
Batteries are particularly good at storing electrical energy for later usage. Its getting the electrical energy out of a battery fast enough that can sometimes create difficulties. During the storage of electrochemical energy in a battery, chemical interconversions of the electrode materials occur usually with concomitant phase changes. Although the overall energy changes can be conducted in a relatively reversible thermodynamic route, the charge and discharge processes in a storage battery often involve irreversibility in inter-conversions of the chemical electrode-reagents. Accordingly, the cycle-life of storage batteries is usually limited, and varies with the battery type. Capacitors are at the opposite end of the scale. They store power as static electricity rather than in the reversible, faradic chemical reaction found in a
The specific energy is given by:
Specific energy = U I t m
(1)
where
U[V] is voltage, I[A] electric current, t[s] time and m[kg] mass. The specific power is:
Specific power =
U I m
(2)
The main differences between the performances of supercapacitors and accumulators can be easily noticed as in table 1 [5]:
978-1-4244-50330309/$26.00 2009 IEEE
196
17-20 Sep 2009, Gyula, Hungary
SIITME2009 15th International Symposium for Design and Technology of Electronics Packages
Accumulators Faradic reactions Mass transfer between the electrodes
Energy storage method
Supercapacitors Mostly electrostatic interactions Ionic charge accumulation at the active material/electrolyte interface
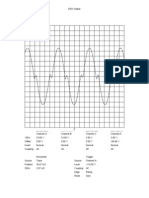
precision digital multimeter Fluke 8845A. The voltage on the supercapacitor is recorded every second, and by plotting this voltage versus time is obtained the graph presented in Figure 3.
Volatge on ECOND PSCAP350
12
10
Voltage[V]
Discharge curve Depending on cycling profile Impact of the active material degradation and parasitic phenomena such as electrolyte degradation 60 Wh/kg (alkaline) 140 Wh/kg (Li-ion) 0.4-0.8 kW/kg (alkaline) 0.3-1.5 kW/kg (Liion)
Cycle life
>>1 000 000 Impact of parasitic phenomena such as electrolyte degradation
0 0 200 400 600 Tim e[s] 800 1000
Fig. 3. Voltage from screening test using Econd PScap350.
Energy level Power level
1-10 Wh/kg
1-6 kW/kg
We used a model for our supercapacitor starting from a model proposed in [5], [6]. The Spice model is presented in figure 4 and the Simulink model is presented in figure 5.
R1 4m
Tab. 1. Acumulators versus supercapacitors.
3. MODELING OF SUPERCAPACITORS EXTRACTION OF PARAMETERS
Starting from experimental results, we extract the parameters. For experimental measurements one used the supercapacitor Econd PScap350. Table 2 presents the specified parameters for this supercapacitor:
Parameter Nominal Voltage Nominal Capacitance Mass Value 14 [V] 350 [F] 24 [kg]
0
S1 I1
+ +
Rp 10m
C1 23
S VOFF = 11.07V VON = 11.05V R3 10
R2 200
C 300
Tab. 2. Specific parameters for Econd PScap350.
The measurement consist of charging the supercapacitor at a current of 10A, until the voltage on the supercapacitor reaches the value 11V, as it was set, then the current is cut off for about 10 minutes. After that, a negative current of -20A was applied, in order to discharge the supercapacitor. For discharging the supercapacitor one used an electronic load from Chroma. The experimental data was recorded with a
Fig. 4. The Spice model of the supercapacitor.
Using the experimental results presented in figure 3, we can calculate the parameters of the model presented in figure 4. The capacitance value (C) can then be calculated using:
978-1-4244-50330309/$26.00 2009 IEEE
197
17-20 Sep 2009, Gyula, Hungary
SIITME2009 15th International Symposium for Design and Technology of Electronics Packages
C=
Q U
(3)
Q = i (t )dt is charge and
The measurement points that are selected in our case are: (316s; 11.062V) and (317s; 11.042V). The value on R1 is:
R1 = 11.062V 11.042V 0.02 = = 0.002 = 2m 10 A 10
where
U is voltage. In order to calculate this value, we choose the time period when the voltage rise from 2V up to 9V. From figure 3, we can observe that the time is:
t = 255 46 = 209[ s]
(9)
(4)
and the charge will be:
Q = 10[ A] 209[ s ] = 2090[C ]
Since the self discharge is low, the value of the R2 resistance is hard to acquire from measurement analysis. A slow discharge means that the resistance value must be high, but according to our measurements, the self-discharge is not very slow. A conclusion from the observed results is that a good estimate value on the resistance is 200 . R3 is the name of the resistance used in the balancing circuit. The value on the resistance R3 can be calculated by measuring the voltage drop after the charging current has been turned off. The resistance value can be calculated using:
R3 = t u ln 1 C u 0
(5)
Using the equation (3) we can calculate the main capacitance of the supercap:
C= Q 2090C = = 298.57 F 300 F 7V U
(6) (10)
The value of the capacitance C1 is chosen to be one thirteenth of C. The capacitance C1 illustrates the influence of the voltage in the total capacitance of supercapacitor. The impact of the C1 component in the model is very small, which means that a change in its value does not impact model accuracy much. The value for C1 is:
Cp = C 300 = 23F 13 13
where u0 and u1 are the first and second voltage points. The measurements points that are chosen: (316s; 11.062V), the maximum point on the charging curve, and (376s; 10.895V).
R3 = t 60s = 10 u1 10.895 300 F ln C ln u 11.062 0
(7)
(11)
The value of the series resistance R1 can be found by observing a rapid change in charging current and measuring the initial voltage variation. This voltage variation has a steeper inclination than the variation that occurs right after because of the supercapacitor self-discharge. The variation corresponds to the voltage drop over the resistance R1. The value on R1 is calculated using the voltage drop that occurs right after the current is cut off. Using the following equation:
R1 = u i
4. SIMULATION RESULTS
The Simulink model of the basic circuit for the supercapacitor is presented in Figure 5. The relay block controls the switch that connects the balancing resistance R3 to the circuit. Since that part of the circuit is supposed to keep the voltage over the supercapacitor from rising too high, it is set to be connected when the voltage goes above 11.07V. It is disconnected when the voltage goes below 11.05V. These voltage values are selected after studying the measured voltage curve where it can be seen that a significant derivative change occurs after a voltage peak at 11.05V. This derivative change can be interpreted to occur because of the connection of the
198 17-20 Sep 2009, Gyula, Hungary
(8)
978-1-4244-50330309/$26.00 2009 IEEE
SIITME2009 15th International Symposium for Design and Technology of Electronics Packages
extra resistance since the increased load means that the voltage increases slower. The relay block in Simulink can only be set to have a turn on value that is larger than or equal to the turn off value which is why turn on is set to 11.07 V. The protection provided by this circuit is important because supercapacitors are sensitive to over voltage.
the current is cut off. It can be noticed a slow selfdischarge in time. The moment when a negative current of -20A is applied, the voltage on the supercapacitor decreases, having a double slope when compared to the charging curve. Figure 7 highlights the sudden voltage variation the moment when the negative current is applied.
Voltage on ECOND PSCAP350 11.1 11 10.9 10.8 Voltage[V] 10.7 10.6 10.5 10.4 10.3 10.2
X: 786.1 Y: 10.88
X: 786.5 Y : 10.84
800 Time[s]
Fig. 7. Steeper voltage variation due to the negative current. Fig. 5. The Simulink model of the supercapacitor.
The values of the components previous computed are applied for this Simulink model. The simulation time was set to be 1030s, a current vector was specified in Matlab Command Window, then by plotting time versus voltage, the result in Figure 6.
Voltage on ECOND PSCAP350 12
The same basic circuit model for supercapacitor is implemented in Orcad PSpice, in order to compare the results obtained experimentally and in Simulik program. By modeling in OrCAD, the circuit consists entirely of regular electrical components, as shown in Figure 4. Current and voltage on the supercapacitor are presented in figure 8.
10A
10
8 Voltage[V]
-0A
-10A
SEL>> -21A I(I1)
2
12V
200
400
600 Time[s]
800
1000
8V
Fig. 6. The Simulink result for voltage on supercapacitor Econd PScap.
4V
As it can be observed, the result is very similar to the measurement data. When the supercapacitor is charged at 10 A, the voltage increases almost linearly, and then it has approximately the same value when
978-1-4244-50330309/$26.00 2009 IEEE 199
0V 0s 0.2Ks -V(R1:2) 0.4Ks 0.6Ks Time 0.8Ks 1.0Ks 1.2Ks
17-20 Sep 2009, Gyula, Hungary
SIITME2009 15th International Symposium for Design and Technology of Electronics Packages
Fig. 8. Current (up) and voltage (down) on the supercapacitor.
The voltage increases linearly during the time interval when the 10A current is applied, then is has a slow self discharge as long as the current is cut off. By applying a negative current of -20A, the supercapacitor discharges, having a double slope when compared to the charging curve. The same observation, that the result is very similar to the measurement data, can be made analyzing this result in Orcad.
10.8V
presented in the paper. The results prove the accuracy of the models and of the method used to compute the components values.
ACKNOWLEDGEMENTS
The application was developed on the frame of PNII TRANS-SUPERCAP Romanian national project no. D21018/2007.
REFERENCES
[1] L. D. Druxman, Power Conversion from Environmentally Scavenged Energy Sources, Sandia National Laboratories, Livermore, California, 2000. [2] R. Signorelli, J. Schindall, J. Kassakian, Carbon Nanotube Enhanced Double Layer Capacitor, Proceedings of 14th International Seminar on Double Layer Capacitors and Similar Energy Storage Devices. Deerfield Beach, FL: Florida Educational Seminar, pp. 49-61, 2004. [2] http://www.batteryuniversity.com [3] F. Belhachem, S. Ral, B. Davat, A physical based model of power electric double-layer supercapacitors, Proceeding of Industry Applications Conference, vol.5, pp. 3069-3076, 2000. [4] Anthony Green The Non-Battery Battery-The Potential Role of Supercapacitors in Standby Power Applications, The Battcon 2002 Proceedings, Ft. Lauderdale, Florida, USA, 2002, http://www.battcon.com/PapersFinal2002/GreenPaper2 002.pdf [5] P. Johansson, B. Andersson, Comparison of Simulation Programs for Supercapacitor Modelling. Model Creation and Verification, Chalmers University of Technology, Sweden, 2008. [6] A. Grama, D. Petreu, R. Gltu, I. Ciocan, Equivalent Models Study of Supercapacitors Behavior, Proceedings of 14th International Symposium for Design and Technology of Electronic Packages (SIITME 2008), pp. 50-54, 2008.
10.0V
9.0V
8.0V
684.7s -V(R1:2)
720.0s
760.0s Time
800.0s
836.7s
Fig. 9. Voltage steeper variation by applying the negative current.
The voltage steeper variation by applying the negative current can be see in figure 9.
5. CONCLUSIONS
In this paper two models used for modeling the supercapacitor are presented. One model is developed using Simulink 7.5 and the second model is implemented in Orcad 9.2. The model parameters are extracted from experimental measurements using a supercapacitor Econd PScap350. The measurement consist of charging the supercapacitor at a current of 10A, until the voltage on the supercapacitor reaches the value 11V, as it was set, then the current is cut off for about 10 minutes. After that, a negative current of -20A was applied, in order to discharge the supercapacitor. The voltage on the supercapacitor is recorded every second, by a precision digital multimeter Fluke 8845A. A method for computing the parameters values (using significant points from measurement data) is
978-1-4244-50330309/$26.00 2009 IEEE
200
17-20 Sep 2009, Gyula, Hungary
Vous aimerez peut-être aussi
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeD'EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeÉvaluation : 4 sur 5 étoiles4/5 (5794)
- KhmerKeyboard NiDA V1.0Document1 pageKhmerKeyboard NiDA V1.0Leng SovannarithPas encore d'évaluation
- The Little Book of Hygge: Danish Secrets to Happy LivingD'EverandThe Little Book of Hygge: Danish Secrets to Happy LivingÉvaluation : 3.5 sur 5 étoiles3.5/5 (399)
- Part IIDocument281 pagesPart IILeng SovannarithPas encore d'évaluation
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryD'EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryÉvaluation : 3.5 sur 5 étoiles3.5/5 (231)
- FC-GEE-8 - Electrical Transmission and DistributionDocument1 pageFC-GEE-8 - Electrical Transmission and DistributionLeng SovannarithPas encore d'évaluation
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceD'EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceÉvaluation : 4 sur 5 étoiles4/5 (894)
- Bridgelux Introduces More Compact COB LEDs For Retrofit Lamps - LEDsDocument9 pagesBridgelux Introduces More Compact COB LEDs For Retrofit Lamps - LEDsLeng SovannarithPas encore d'évaluation
- The Yellow House: A Memoir (2019 National Book Award Winner)D'EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Évaluation : 4 sur 5 étoiles4/5 (98)
- 2.3.7. Detailed Description of The Effective MassDocument4 pages2.3.7. Detailed Description of The Effective MassDr-Syed Zulqarnain HaiderPas encore d'évaluation
- Shoe Dog: A Memoir by the Creator of NikeD'EverandShoe Dog: A Memoir by the Creator of NikeÉvaluation : 4.5 sur 5 étoiles4.5/5 (537)
- Philips Lumileds Launches New Lime LED and Multi-Emitter Package, Demos at SIL - LEDsDocument3 pagesPhilips Lumileds Launches New Lime LED and Multi-Emitter Package, Demos at SIL - LEDsLeng SovannarithPas encore d'évaluation
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureD'EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureÉvaluation : 4.5 sur 5 étoiles4.5/5 (474)
- An Introduction To Interpolation Theory, 2007 (Lunardi - A.)Document125 pagesAn Introduction To Interpolation Theory, 2007 (Lunardi - A.)Leng SovannarithPas encore d'évaluation
- Never Split the Difference: Negotiating As If Your Life Depended On ItD'EverandNever Split the Difference: Negotiating As If Your Life Depended On ItÉvaluation : 4.5 sur 5 étoiles4.5/5 (838)
- 8) Controlling LED Brightness Using PWM - WFFwikiDocument5 pages8) Controlling LED Brightness Using PWM - WFFwikiLeng SovannarithPas encore d'évaluation
- Grit: The Power of Passion and PerseveranceD'EverandGrit: The Power of Passion and PerseveranceÉvaluation : 4 sur 5 étoiles4/5 (587)
- NTC ThermistorsDocument44 pagesNTC Thermistorskn65238859Pas encore d'évaluation
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaD'EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaÉvaluation : 4.5 sur 5 étoiles4.5/5 (265)
- 1 s2.0 0003491680902882 MainDocument14 pages1 s2.0 0003491680902882 MainLeng SovannarithPas encore d'évaluation
- RNDocument62 pagesRNLorenzo CarrieriPas encore d'évaluation
- ADocument1 pageAmiguel_maahPas encore d'évaluation
- The Emperor of All Maladies: A Biography of CancerD'EverandThe Emperor of All Maladies: A Biography of CancerÉvaluation : 4.5 sur 5 étoiles4.5/5 (271)
- 8) Controlling LED Brightness Using PWM - WFFwikiDocument5 pages8) Controlling LED Brightness Using PWM - WFFwikiLeng SovannarithPas encore d'évaluation
- On Fire: The (Burning) Case for a Green New DealD'EverandOn Fire: The (Burning) Case for a Green New DealÉvaluation : 4 sur 5 étoiles4/5 (73)
- 9) Usb RGB Led Vu Meter - WffwikiDocument4 pages9) Usb RGB Led Vu Meter - WffwikiLeng Sovannarith100% (2)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersD'EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersÉvaluation : 4.5 sur 5 étoiles4.5/5 (344)
- 8) Controlling LED Brightness Using PWM - WFFwikiDocument5 pages8) Controlling LED Brightness Using PWM - WFFwikiLeng SovannarithPas encore d'évaluation
- Team of Rivals: The Political Genius of Abraham LincolnD'EverandTeam of Rivals: The Political Genius of Abraham LincolnÉvaluation : 4.5 sur 5 étoiles4.5/5 (234)
- Philips Lumileds Launches New Lime LED and Multi-Emitter Package, Demos at SILDocument6 pagesPhilips Lumileds Launches New Lime LED and Multi-Emitter Package, Demos at SILLeng SovannarithPas encore d'évaluation
- 9) Usb RGB Led Vu Meter - WffwikiDocument4 pages9) Usb RGB Led Vu Meter - WffwikiLeng Sovannarith100% (2)
- Connector: 2.0mm Pitch/disconnectable Crimp Style ConnectorsDocument3 pagesConnector: 2.0mm Pitch/disconnectable Crimp Style ConnectorsLeng SovannarithPas encore d'évaluation
- Mikro CDocument6 pagesMikro CLeng SovannarithPas encore d'évaluation
- Bridgelux Introduces More Compact COB LEDs For Retrofit Lamps - LEDsDocument9 pagesBridgelux Introduces More Compact COB LEDs For Retrofit Lamps - LEDsLeng SovannarithPas encore d'évaluation
- The Unwinding: An Inner History of the New AmericaD'EverandThe Unwinding: An Inner History of the New AmericaÉvaluation : 4 sur 5 étoiles4/5 (45)
- Electrical Power Supply and DistributionDocument122 pagesElectrical Power Supply and Distributionmmalamuti9325100% (4)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyD'EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyÉvaluation : 3.5 sur 5 étoiles3.5/5 (2219)
- Extrapolation MethodsDocument39 pagesExtrapolation MethodsLeng SovannarithPas encore d'évaluation
- FC-GEE-9 Electrical Transmission and DistributionDocument1 pageFC-GEE-9 Electrical Transmission and DistributionLeng SovannarithPas encore d'évaluation
- Philips Lumileds Launches New Lime LED and Multi-Emitter Package, Demos at SIL - LEDsDocument3 pagesPhilips Lumileds Launches New Lime LED and Multi-Emitter Package, Demos at SIL - LEDsLeng SovannarithPas encore d'évaluation
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreD'EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreÉvaluation : 4 sur 5 étoiles4/5 (1090)
- FC GEE 8 Electrical TransientDocument2 pagesFC GEE 8 Electrical TransientLeng SovannarithPas encore d'évaluation
- PIC12F508/509/16F505 Data Sheet: 8/14-Pin, 8-Bit Flash MicrocontrollersDocument99 pagesPIC12F508/509/16F505 Data Sheet: 8/14-Pin, 8-Bit Flash MicrocontrollersJon LópezPas encore d'évaluation
- Electrical Power Supply and DistributionDocument122 pagesElectrical Power Supply and Distributionmmalamuti9325100% (4)
- FC GEE 8 Electrical TransientDocument2 pagesFC GEE 8 Electrical TransientLeng SovannarithPas encore d'évaluation
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)D'EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Évaluation : 4.5 sur 5 étoiles4.5/5 (119)
- FC GEE 8 Electrical TransientDocument2 pagesFC GEE 8 Electrical TransientLeng SovannarithPas encore d'évaluation
- FC GEE 8 Electrical TransientDocument2 pagesFC GEE 8 Electrical TransientLeng SovannarithPas encore d'évaluation
- IEM Mobil O Graph ManualDocument92 pagesIEM Mobil O Graph ManualHomo CyberneticusPas encore d'évaluation
- Electrochemical EnergyDocument18 pagesElectrochemical EnergyJay Wilmar Huelar100% (1)
- INDUSTRIAL FAN PROVIDES COOL COMFORTDocument10 pagesINDUSTRIAL FAN PROVIDES COOL COMFORTPengadaan RSUDKPas encore d'évaluation
- Oes Catlog 2020 v5Document58 pagesOes Catlog 2020 v5ramiz razaPas encore d'évaluation
- Dc-Ac Inverters: Owner's ManualDocument32 pagesDc-Ac Inverters: Owner's Manualalex castroPas encore d'évaluation
- Ac AssignmentDocument3 pagesAc AssignmentAditya GuptaPas encore d'évaluation
- Xartu1 ManualDocument63 pagesXartu1 ManualjesusPas encore d'évaluation
- Trimble SPS985 GNSS Smart Antenna: Getting Started GuideDocument34 pagesTrimble SPS985 GNSS Smart Antenna: Getting Started GuideTony KagelPas encore d'évaluation
- MPPT Solar Charge Controller Instruction ManualDocument12 pagesMPPT Solar Charge Controller Instruction ManualNkosilozwelo SibandaPas encore d'évaluation
- EverStart MaxxDocument20 pagesEverStart MaxxEric DuttonPas encore d'évaluation
- Her Body and Other Parties: StoriesD'EverandHer Body and Other Parties: StoriesÉvaluation : 4 sur 5 étoiles4/5 (821)
- Technical Manual - UP Range - 03Document51 pagesTechnical Manual - UP Range - 03Emad OthmanPas encore d'évaluation
- Reolink Go PT Series Quick Start Guide April 2022Document49 pagesReolink Go PT Series Quick Start Guide April 2022Claire LouisePas encore d'évaluation
- Debi Prasad Dash - ARAI-PIP Presentation PDFDocument39 pagesDebi Prasad Dash - ARAI-PIP Presentation PDFvarun sharmaPas encore d'évaluation
- 2021 Aprilia RS660 and Tuono 660 Service ManualDocument420 pages2021 Aprilia RS660 and Tuono 660 Service ManualApriliaPas encore d'évaluation
- Ibot - Robotics Club of Iit Madras Tutorial 1.1.1 Build Your Basic BotDocument21 pagesIbot - Robotics Club of Iit Madras Tutorial 1.1.1 Build Your Basic BotJavier Dorado SánchezPas encore d'évaluation
- Understanding Voltage Behavior of Lithium-Ion Batteries in Electric Vehicles ApplicationsDocument17 pagesUnderstanding Voltage Behavior of Lithium-Ion Batteries in Electric Vehicles Applicationsrudraee41Pas encore d'évaluation
- CORDLESS PLUNGE SAW PTS 20-Li A1 PDFDocument68 pagesCORDLESS PLUNGE SAW PTS 20-Li A1 PDFΑλεξης ΝεοφυτουPas encore d'évaluation
- Electricity Electronics Test Banswer KeyDocument6 pagesElectricity Electronics Test Banswer KeyGary Nugas0% (1)
- Remington HC7150 ProPower Hair ClipperDocument148 pagesRemington HC7150 ProPower Hair ClipperGheorghiu Malita TamaraPas encore d'évaluation
- Be FR NLDocument198 pagesBe FR NLNaltu IonelPas encore d'évaluation
- HR12-650WL (v.17)Document2 pagesHR12-650WL (v.17)GeorgePas encore d'évaluation
- Sony A7s Manual PDFDocument96 pagesSony A7s Manual PDFVasco DiasPas encore d'évaluation
- BAE SECURA PVS SOLAR Technical SpecificationDocument2 pagesBAE SECURA PVS SOLAR Technical SpecificationNguyễn Anh DanhPas encore d'évaluation
- Molicel Li BatteryDocument1 pageMolicel Li BatteryShyam SrinivasanPas encore d'évaluation
- Techfill Nicad Manual - T-SeriesDocument25 pagesTechfill Nicad Manual - T-Seriesvideo irfanPas encore d'évaluation
- User Instruction Manual: Hoyer AdvanceDocument22 pagesUser Instruction Manual: Hoyer AdvanceGuilhermePas encore d'évaluation
- PH 1100 L Operating ManualDocument74 pagesPH 1100 L Operating ManualAlex VallesterosPas encore d'évaluation
- AH Sharp ShooterDocument4 pagesAH Sharp ShooterBernardo AlvaradoPas encore d'évaluation
- Safety Manual B1Document78 pagesSafety Manual B1parthasarathipkPas encore d'évaluation
- Lithium Ion Technical ManualDocument13 pagesLithium Ion Technical ManualTapabrata DamPas encore d'évaluation