Multi-Degree of Freedom Systems

1
1. General n-degree of freedom vibration system
1.1. Matrices in the equations of motion
| |{ } | |{ } | |{ } { } ( ) M x C x K x F t + + = `` `` ``

when
| |
1 11 12 1
2 21 22 2
1 2
0 0
0 0

0
0
n
n
n n n nn
m m m m
m m m m
M
m m m m
( (
( (
( (
= =
( (
( (
( (

. . . .






| |
11 12 1
21 22 2
1 2
=
n
n
n n nn
k k k
k k k
K
k k k
(
(
(
(
(
(

. . .

1.2. Positive definite & Positive semi-definite.

<Definition> Positive definiteness
An nn matrix
| |
11 12 1
21 22 2
1 2
n
n
n n nn
m m m
m m m
M
m m m
(
(
(
=
(
(

. . .

is positive definite if for any given vector

{ }
1
2
n
x
x
x
x



=
`


)
.
,
{ }
| |
{ } 0
T
x M x and
{ }
| |
{ } 0
T
x M x = if and only if { } 0 x = .

usually diagonal for
lumped-mass &
stiffness systems
In general, it is an n by n
positive definite matrix.
In general, its an nxn matrix.
It usually has a narrow diagonal bandwidth.
In general, it is positive semi-definite.
If there is no rigid body mode allowed, it
should be positive definite.
Multi-Degree of Freedom Systems
2
<Theorm> Positive Definiteness of the mass matrix
The mass matrix
| |
1
2
0 0
0 0
0
0 0
n
m
m
M
m
(
(
(
=
(
(

. .

is positive definite.
[proof]
Consider the kinetic energy of a vibration system
( ) ( ) ( ) { }
| |
{ }
2 2 2
1 1 2 2
1 1 1 1
= + + + =
2 2 2 2
T
k n n
E m x m x m x x M x ` ` ` ` `
where { }
1
2
=
n
x
x
x
x



`


)
`
`
.
`
and
| |
1
2
0 0
0 0
=
0
0 0
n
m
m
M
m
(
(
(
(
(

. .

.
Since 0
k
E and =0
k
E if and only if { } { } = 0 x` , the mass matrix | |
M
is positive definite.

<Definition> Positive Semi-Definiteness
A nn matrix
| |
11 12 1
21 22 2
1 2
=
n
n
n n nn
k k k
k k k
K
k k k
(
(
(
(
(

. . .

is positive semi-definite if for any given vector

{ }
1
2
=
n
x
x
x
x



`


)
.
,
{ }
| |
{ } 0
T
x K x .

Multi-Degree of Freedom Systems
3
<Theorem> Positive semi-definiteness of the stiffness matrix
The stiffness matrix
| |
11 12 1
21 22 2
1 2
=
n
n
n n nn
k k k
k k k
K
k k k
(
(
(
(
(

. . .

is positive semi-definite.
[Proof]
Consider the process which make the system change from { }
0
0
0
0
x



=
`


)
.
to { }
1
2
n
n
x
x
x
x



=
`


)
.


1
st
process: { }
0
0
0
0
x



=
`


)
.
{ }
1
1
0
0
x
x



=
`


)
.
i.e. x
1
changes from 0 to x
1
while x
j
= 0 for all
j > 1. ( x
j
is constrained such that x
j
= 0.)

2
nd
process : { }
1
1
0
0
x
x



=
`


)
.
{ }
1
2
2
0
0
x
x
x




=
`



)
.
i.e. x
2
changes from 0 to x
2
while x
1
= x
1
and
x
j
= 0 for all j > 2.

i-th process : { }
1
1
1
1
0
0
0
i
i
x
x
x
x

=
`





)
.
.
{ }
1
1
1
0
0
i
i
i
x
x
x
x
x

=
`





)
.
.
i.e. x
i
changes from 0 to x
i
while x
1
= x
1
,
x
2
= x
2
, .. , x
i-1
= x
i-1
, and x
j
= 0 for all j > i.
i-th
Multi-Degree of Freedom Systems
4
n-th process : { }
1
2
1
1
0
n
n
x
x
x
x

=
`



)
. { }
1
2
1
n
n
n
x
x
x
x
x

=
`



)
. i.e. x
n
changes from 0 to x
n
while and
x
j
= x
j
for all j < n so that the final of the system the whole process become the desired state {x}
n
.

Now calculate the potential energy. The increase of the potential energy through the each sub-process
can be calculated as follows:
1
st
process:
1 1
2
1 1 1 11 1 1 11 1
0 0
1
( ) ( )
2
x x
p
E Fdx k x dx k x = = =


( Since 0 1
j
x j = , no contribution is made by the force exerted on 1
j
m j )
2
nd
process:
2 2
2
2 2 2 21 1 22 2 2 21 1 2 22 2
0 0
1
( ) ( ) ( )
2
x x
p
E F dx k x k x dx k x x k x = = + = +


. . .
i-th process:
1 1 2 2
0 0
2
1 1 2 2 ( 1) 1
( )
1
( )
2
i i
x x
p i i i i i ii i i
i i i i i i i i ii i
E Fdx (k x k x k x )dx
k x x k x x k x x k x

= = + + +
= + + + +

. . .
n-th process:
1 1 2 2
0 0
2
1 1 2 2 ( 1) 1
( )
1
( )
2
n n
x x
p n n n n n nn n n
n n n n n n n n nn n
E F dx (k x k x k x )dx
k x x k x x k x x k x

= = + + +
= + + + +

Therefore, the potential energy of the final state will be

=

= = =
|
|
.
|

\
|
+
)
`

= =
n
i
i
j
j i ji
n
i
i ii
n
i
i p p
x x k x k E E
2
1
1 1
2
1
) (
2
1
) (



If [K] is symmetric, then
1 1
2
2 1 2 1 1 1 1
1 1
( )
2 2
n i n i n n n
ji i j ij i j ij i j ii i
i j i j i j i
k x x k x x k x x k x

= = = = = = =
| | | |
= =
| |
\ . \ .


11
21 22
31 32 33
41 42 43 44
1 2 3 4 n n n n nn
k
k k
k k k
k k k k
k k k k k
(
(
(
(
(
(
(
(
(

. . . .

Multi-Degree of Freedom Systems

5
Therefore { } | |{ }
1 1
1 1
2 2
n n
T
p ij i j
i j
E k x x x K x
= =
= =

Since E
p
is always non-negative, [K] is positive semi-definite.
Note that E
p
= 0 when the system moves in a rigid body translation. Hence, E
p
= 0 even when
{x}{0}. This implies that [K] is not positive definite sometimes. Therefore, we can guarantee that
[K] is positive semi-definite only.

<Theorem> The stiffness matrix is symmetric.
[Proof] Now we will try to prove that [K] is symmetric.
Consider the two processes. Process and Process .
Process
-1
st
process: { }
0
0
0
0
I
x




=
`


)
.
{ }
1
0
0
0
0
0
0
0
0
i
I
x
x










=
`








)
.
.
.


-2
nd
process: { }
1
0
0
0
0
0
0
0
0
i
I
x
x










=
`








)
.
.
.
{ }
2
0
0
0
0
0
0
0
i
I
j
x
x
x

=
`








)
.
.
.

j-th
j-th
i-th
i-th
i-th
j-th
Multi-Degree of Freedom Systems
6

Process :
-1
st
process: { }
0
0
0
0
0
0
0
0
0
0
II
x










=
`








)
.
.
.
{ }
1
0
0
0
0
0
0
0
0
II
j
x
x

=
`








)
.
.
.


-2
nd
process : { }
1
0
0
0
0
0
0
0
0
II
j
x
x

=
`








)
.
.
.
{ }
2
0
0
0
0
0
0
0
i
II
j
x
x
x

=
`








)
.
.
.

The potential energy obtained by the process, Process
2 2
1 1
( ) ( ) ( )
2 2
P I ii i jj j ji i j
E k x k x k x x = + +
The potential energy obtained by process
2 2
1 1
( ) ( ) ( )
2 2
P II jj j ii i ii j i
E k x k x k x x = + +
Since the final state is identical and the potential energy is determined by the state independently
the process through which the final state is achieved
ij ji P P
k k E E = = ) ( ) (

i-th
j-th
i-th
j-th
i-th
j-th
i-th
j-th
Multi-Degree of Freedom Systems
7
Since i, j are arbitrarily chosen, ,
ij ji
k k i j = [ K] is symmetric.

This completes the proof of the theorem [K] is positive semi-definite.

2. Responses of n-degree of freedom systems
z It is time to go back to the equation of motion for the multi-degree of freedom vibration system.
z The main idea of the method is that we can solve the coupled n-differential equations by a proper
transformation and by solving the uncoupled n-differential equations.
z The problem or questions is how we can find an appropriate transformation that makes the coupled
n-differential equations into uncoupled n-differential equations

2.1. Solving Technique
Suppose we can find a linear transformation such that
{ } | |{ } x z = i.e.
1 1 11 12 1
2 21 22 2 2
1 2
( ) ( )
( ) ( )
( ) ( )
n
n
n n nn n n
x t z t
x t z t
x t z t



(
(

(
=
` `
(

(

) )

. . . . .

and
| | | || | | |
1
1 0 0
0 1 0
0 0 1
M I

(
(
(
= =
(
(

. . .

and
| | | || |
1 1
1
2 2
2 0 0
0
0 2 0
2
0
0 0 2
n n
n n
C

(
(
(
(
(
= =
(
(
(
(

. . .

and

| | | || |
2
1
2
1
2 2
2
0 0
0
0 0
0
0 0
n
n
K

(
(
(
(
(
= =
(
(
(
(

(

. . .

.

Multi-Degree of Freedom Systems
8
The equation of motion
| |{ } | |{ } | |{ } { } M x C x K x F + + = `` `
Since { } { } [ ] x z = `` `` , { } { } [ ] x z = ` ` , { } { } [ ] x z = , Eq. can be re-written as
| || |{ } | || |{ } | || || | { } M z C z K z F + + = `` `
Now Multiply the both side of Eq by
| |
T
to yield
| | | || |{ } | | | || |{ } | | | || || | | | { }
T T T T
M z C z K z F + + = `` `
By the assumption, becomes
{ } { } { } | | { }
2
0 0
2
0 0
T
n n n
z z z F
( (
( (
+ + =
( (
( (


`` `


or
2
1
2 1, 2, , 3
n
i i i i ji j
j
z z z F i
=
+ + = =

`` `
since
ji
is the component of []
T
at i-th row and j-th column.
Eq implies a set of independent n-differential equations whose solutions are known as
( ) ( ) ( )
( ) ( )
( )
( )
0 0
0
1
0
1
cos sin
1
sin
i i
i i
t i i i i
i i id id
id
n
t
t
j id
ij
j
id
z z
z t e z t t
F e t dt

=
+
= +
`
)

( +
`

)

`

Once all the z
i
(t)s are obtained, the response of the system {x(t)} can be obtained by using the
transformation {x(t)} = []{z(t)} i.e. ( ) ( )
1
n
i ij j
j
x t z t
=
=

.
Therefore, the response (, whether free or forced, ) of the system can be easily obtained. The
remaining question is Does there exist such a matrix [] ?
The answer is Yes. So, we will show how to find it!

2.2. Normalization with respect to Mass Matrix [M]
For many vibration systems, the mass matrix is a diagonal matrix, i.e.
Multi-Degree of Freedom Systems
9
| |
1
2
3
0 0 0
0 0 0
0 0 0
0 0 0
n
m
m
M m
m
(
(
(
( =
(
(
(

. . . .

.
Note that [M] is symmetric. Now consider
1
2
1/ 2
3
1/ 0 0 0
0 1/ 0 0
0 0 1/ 0
0 0 0 1/
n
m
m
M
m
m

(
(
(
(
( =
(
(
(
(

. . . .

.
Then,
| | | |
1/ 2 1/ 2
1 0 0
0 1 0
0 0 1
T
M M M I

(
(
(
( ( = =

(
(

. . .

.
Consider a new variables { }
1
2
( )
( )
( )
( )
n
y t
y t
y t
y t



=
`


)
.
such that { } { }
1/ 2
x M y

( =

.
Then, the equation of motion will be
| | { } | | { } | | { } { }
1/ 2 1/ 2 1/ 2
M M y C M y K M y F

( ( ( + + =

`` `
4

Multiply the both sides of Eq. by
1/ 2
T
M

(

to yield
| | { } | | { }
| | { } { }
1/ 2 1/ 2 1/ 2 1/ 2
1/ 2 1/ 2 1/ 2

T T
T T
M M M y M C M y
M K M y M F


( ( ( ( +

( ( ( + =

`` `

{ } | | { } | | { } { }
1/ 2 1/ 2 1/ 2 1/ 2 1/ 2
T T T
y M C M y M K M y M F

( ( ( ( ( + + =

`` `
Let
| |
1/ 2 1/ 2
T
K M K M

( ( ( =

. Note that K (

is symmetric.

Multi-Degree of Freedom Systems
10
2.3. Diagonalization of K (


For simplicity, consider the case that the damping force is zero. i.e.
| |
0 C . Then, Eq can be
reduced to the following:
{ } { } { }
1/ 2
T
y K y M F

( ( + =

``
Does there exist a transformation matrix [] such that
| | | |
2
1
2
1
2 2
2
0 0
0
0 0
0
0 0
n
n
K

(
(
(
(
(
( = =

(
(
(
(

(

. . .

.
Now we can use the important theorem in Linear Algebra.

<Theorem> Similarity
Every real symmetric matrix is orthogonally similar to a real diagonal
matrix.
<Definition> Orthogonal Matrix.
For a n X n matrix [], [] is orthogonal if []
T
[] = [I]
This implies that []
T
= []
-1
!
<Definition> Similarity.
Two nXn matrices [A] and [B] are similar if there exists a (transformation)
matrix [] such that []
-1
[A][]=[B].

The theorem Every real symmetric matrix is orthogonally similar to a real diagonal matrix.
implies that: For a real nn symmetric matrix K
(

, there exists a transformation matrix []
that is orthogonal such that
Multi-Degree of Freedom Systems
11
| | | | | | | |
2
1
2
1
2 2
2
0 0
0
0 0
0
0 0
T
n
n
K K

(
(
(
(
(
( (
= = =
(
(
(
(

(

. . .

In order that
i
( I = 1, 2, , n ) are real, K
(

should have real non-negative eigenvalues.
This is true because [K] is positive semi-definite.
The proof of this claim is simple. Suppose there exists a negative eigenvalue
i
2
of K
(

,
{ } { } { } | | | |{ } { } { } ( ) ( )
2 2
2
1
0
0
n
T T T T
n i i
i
y K y z K z z z z
=
(
(
( (
= = =
(
(

.
Consider the case that 0
i
z and 0
i
z = i j

.
Then, { } { } ( ) ( )
2 2
0
T
i i
y K y w z
(
= <

. (
i
2
is negative) This is contradiction to the
assumption that K
(

is positive semi-definite.
(We have to prove that if
| |
K is positive semi-definite, so is | |
1 2 1 2
T
K M K M

( ( ( =

.
But it is trivial because | |
1 2 1 2
T
K M K M
( ( ( =


where
1
1 2 2
0 0
0 0
0 0
n
m
m
M
m
(
(
(
( =
(
(
(

. . .

)
Therefore, the equation of motion can be rewritten as
| |{ } | |{ } { }
1 2
T
z K z M F

( ( + =

``
Multiply the both sides of Eq. by []
T
to yield
| | | |{ } | | | |{ } | | { }
1 2
T
T T T
z K z M F

( ( + =

``
Multi-Degree of Freedom Systems
12
{ } { } | | { }
2 1 2
0
0
T
T
n
z z M F

(
(
( + =

(
(

``

or ( )
2
1
( )
n
i i ji j
j
z z F t
=
+ =

`` (i = 1, 2, 3, , n)
where [] = [M
-1/2
][] and
ij
is the i-th row and j-th column component of [].
Note that { } { } | |{ } | |{ }
1 2 1 2
x M y M z z

( ( = = =

.
In other words,
| |{ } | |{ } { } M x K x F + = ``
| || |{ } | || |{ } { } M z K z F + = ``

| | | || |{ } | | | || |{ } | | { }
T T T
M z K z F + = ``
{ } { } | | { }
2
0
0
T
n
z z F
(
(
+ =
(
(

``

For the given initial conditions, { }
10
20
0
0
t
n
x
x
x
x
=



=
`


)
.
, { }
10
20
0
0
t
n
x
x
x
x
=



=
`


)
`
`
`
.
`
and
a given forcing function { }
1
2
( )
( )
( )
n
F t
F t
F
F t



=
`


)
.
,
since []
-1
= ([M
-1/2
][])
-1
= []
-1
[M
-1/2
] = []
T
[M
1/2
] = []
T
[M
-1/2
][M
1/2
][M
1/2
] = []
T
[M
-1/2
]
T
[M] =
([M
-1/2
][])
T
[M] = []
T
[M], we can find the corresponding initial condition for {z(t)} by the following
formula:
Multi-Degree of Freedom Systems
13
{ } | | { }
1 0
1
10
2 0 20
1
0 0
0
0
1
( ) [ ] ( )
n
j j j
j
n
T j j j
j
t t
n
n
jn j j
j
m x
z
m x z
z t M x t
z
m x

=
=
= =
=







= = =
` `


)


)

.
.

{ } | | { }
1 0
1
10
2 0 20
1
0 0
0
0
1
( ) [ ] ( )
n
j j j
j
n
T j j j
j
t t
n
n
jn j j
j
m x
z
m x z
z t M x t
z
m x

=
=
= =
=







= = =
` `


)


)

`
`
` `
` `
.
.
`
`
and
{ } | | { }
1
( )
n
T
ji j
j
Q F F t
=

= =
`
)

or
( )
0 0
1
n
i ji j j
j
z m x
=
=

,
( )
0 0
1
n
i ji j j
j
z m x
=
=

` ` ,
1
( ) ( )
n
i ji j
j
Q t F t
=
( =

.

2.4. Solution
Solve the n-ordinary differential equations:
( )
2
( )
i i i i
z z Q t + = `` with the I.C.
0
(0)
i i
z z = ,
0
(0)
i i
z z = ` ` (i = 1, 2, 3, , n)
When
( )
1
( ) ( )
n
i ji j
j
Q t F t
=
=

| | | | | |
0
0
0
1
cos sin ( ) sin ( )
t
i
i i i i i i
i i
z
z z t t Q t d

= + +

`
.
Since { } | |{ } ( ) ( )
i
x t z t = , | |
1
( ) ( )
n
i il l
l
x t z t
=
=

.

Multi-Degree of Freedom Systems
14
2.5. Modal Analysis
Let { }
i
be the i-th column of the matrix
| | . i.e. { }
1
2
i
i
i
ni

=
`


)
.
.
Note that
{ } | |{ } { } { } { } { }
{ } { }
1 2
1 1
( ) ( ) , , , ( )
( ) ( )
i i
n
n n
i i
i i
i i
x t z t z t
z t z t


= =
( = =

= =



For free vibrations, ( ) 0
i
F t i .
| | | |
0
0
( ) cos sin
i
i i i i
i
z
z t z t t

= +
`
.
If the I.C. is given such that
0
0
i
z and
0
0
j
z = j i and
0
0
j
z = ` j .
Then, { } | |{ }
0
( ) cos
i i
i
x t z t = .

This implies that the response of the system has only one frequency component and the
amplitudes of vibration at other masses are determined if the amplitude of vibration at one
mass is given.

In other words, the free vibration of system can be represented as a superposition of n-fixed-
pattern vibrations with frequencies
1
,
2
, ,
n
.

The fixed pattern of vibration {}
i
corresponding to a natural frequency
i
is called the
corresponding mode shape to a natural frequency
i
.

The combination of a natural frequency,
i
, and its corresponding mode shape is called a
(vibration) mode of the given vibration system.

In the case of forced vibrations, (If {x}
t=0
= {0} and
0
{ } {0}
t
x
=
= ` )
0
1
( ) ( ) sin[ ( )]
t
i i i
i
z t Q t d

0
1 1
1
{ ( )} [ ]{ } ( ){ } { } ( ) sin[ ( )]
n n
t
i i i i i
t t
i
x t z z t Q t d

= =
= = =



Therefore, in the case of forced vibrations, the response of the system can be seen as a
Multi-Degree of Freedom Systems
15
superposition of modal responses.
i-th modal response would be z
i
(t){}
i
. Note that the mode shape is fixed in spite of any
given forcing function.

2.6. Damped System
Now it is time to consider a mechanical vibration system with a damper. The equation of motion will
be as follows;
[ ]{ } [ ]{ } [ ]{ } { } M x C x K x F + + = `` `
There are various mechanisms for damping forces. Hence, it is impossible to show that [C] is
symmetric, or so. But the damping forces are usually very small compared to the spring forces in most
case on structural dynamics.

Now we propose a special case in which the equation of motion can be solved by the
similar method to that for undamped system response.
Suppose [ ] [ ] [ ] C M K = + , i.e. The damping coefficient matrix [C] can be
represented by a sum of a constant () times [M] and a constant () times [K]. Then,
2
1
2
2
2 2
3
2
[ ] [ ][ ] [ ] [ ][ ] [ ] [ ][ ] [ ] [ ][ ] [ ] [ ][ ]
0 0 0
0 0 0
[ ] [ ] 0 0 0
0 0 0
T T T T T
n
n
C M K M K
I





= + = +
( +
(
+
(
(
= + = +
(
(
(
+

. . . .

Another important case is that [C] is such a matrix that
1 1
2 2 2
2 0 0
0
0 2 0
[ ] [ ][ ] 2
0
0 0 2
T
n n
n n
C




(
(
(
(
(
= =
(
(
(
(

. . .

Note that if [ ] [ ] [ ] C M K = + ,
2
1
2 2 2
i
i i
i i



+
= = + . i.e. This is a
special case of the above case. ( i.e.
0
[ ] [ ][ ] 2
0
T
n n
C
(
(
=
(
(

)
Then, The equations of motion will be:
Multi-Degree of Freedom Systems
16
[ ] [ ][ ]{ } [ ] [ ][ ]{ } [ ] [ ][ ]{ } [ ] { }
T T T T
M z C z K z F + + = `` `
2
{ } [ 2 ]{ } [ ]{ } { }
n n n
z z z Q + + =


`` ` or
2
2 ( ) ( )
i i i i i i i
z z z Q t + + = `` ` i = 1,2,3,,n.
The ordinary differential equations
2
2 ( )
i i i i i i i
z z z Q t + + = `` ` can be solved. For
given initial conditions,
( ) ( )
( ) 0 0
0
0
1
( ) { cos[ ] sin[ ]} ( ) sin[ ( )]
( ) ( )
ip ih
i i i i
Z t Z t
t
t t i i i i
i i id id i id
id id
ih ip
z z
z t e z t t Q e t d
z t z t





+
= + +
= +


`

Since
1 1
free vibration terms force vibration terms
induced by the initial induced by the external
condition forces
{ ( )} [ ]{ ( )} ( ){ } ( ){ }
n n
ih i ip i
i i
x t z t z t z t
= =
= = +

_ _
.

2.7. How to find []: modal matrix
Now the question is how we can find the modal matrix [] where [] = [M
1/2
][]. Note that
[] = [M
-1/2
][], consider the i-th column of [], {}
i
. Since [] is orthogonal,
{ } { }
T
i j ij
= . Since
2
0
[ ] [ ][ ]
0
T
n
K
(
(
=
(
(

Note that since
1 1
2 2
[ ] [ ] [ ][ ]
T
K M K M

= ,
2
0 if
{ } [ ]{ }
if
T
i j
j
i j
K
i j

=

=

Since [ ]{ }
j
K is an n-dimensional vector, [ ]{ }
j
K should be linearly dependent on
{}j, i.e.
2
[ ]{ } { }
j j j
K = . Then
2 2 2
{ } [ ]{ } { } { } { } { }
T T T
i j i j j j i j j
K = = =
Therefore, if we find all the eigenvalues and eigenvectors of [ ] K , we can construct pre-
modal matrix such that
1 2
[ ] [{ } ,{ } , ,{ } ]
n
= .
The eigenvectors of [ ] K can be found by solving the eigenvalue problem
Multi-Degree of Freedom Systems
17
2
[ ]{ } { } K = .
Since
1 1
2 2
[ ] [ ] [ ][ ]
T
K M K M

= ,
1
2
[ ]{ } { } M

= and
1 1
2 2
1
[ ] [ ] M M

= ,
Eq becomes
1 1
2 2
2
[ ][ ]{ } [ ]{ } M K M

= .
Multiply by
1
2
[ ] M
1 1
2 2
2 2
[ ]{ } [ ][ ]{ } [ ]{ } K M M M = =

Hence, we can find the modal matrix [] by solving the associated eigenvalue problem,
2
[ ]{ } [ ]{ } K M =

Now lets solve the associated eigenvalue problem

2.8. Solution Method for Eigenvalue Problem
| | | | | | | |
2 2
{ } { } { } 0 K M K M ( = =


In order to { } {0} , | | | |
2
det 0 K M ( =

--- or

2
11 1 12 1
2
12 22 2 2
2
1 2
det 0
n
n
n n nn n
k m k k
k k m k
k k k m

(
(

(
=
(
(

. . .

---
This gives n-th order polynomial equation of
2
. Therefore, we can find n-values for
2
.

Let
1
2
,
2
2
, . ,
n
2
be the n-roots of the polynomial equation. Then, we can find the eigenvector
(or modal vector) by solving the following equation:
2
1 11 1 12 1
2
2 12 22 2 2
2
1 2
0
0
0
i i n
i i n
ni n n nn i n
k m k k
k k m k
k k k m



(
(

(
=
` `
(

(

(
) )

. . . . .

---
Multi-Degree of Freedom Systems
18
Equation provide the direction of i-th modal vector. Hence, first set { }
1
2
i
i
i
i
ni

=
`


)
.

and determine
i
by the orthogonality of the modal matrix, i.e. { } | |{ } 1
T
i i
= and
obviously { } | |{ } 0
T
j i
= if i j .
The modal matrix [] can be constructed by collection the eigenvectors {}
i
, i.e.
| | { } { } { }
1 2
, , ,
n
( =

.


3. Exercises
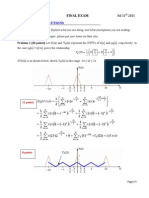
3.1. <Exercise 1>
1 1 2
2 0 mx kx kx + = ``
2 1 2
2 0 mx kx kx + = ``
1 1
2 2
0 2 0
0 2 0
x x m k k
x x m k k
| | | | ( ( | |
+ =
| | | ( (

\ . \ . \ .
``
``

[Step 1] Solve the associated eigenvalue problem.
| |{ } | |{ }
2
K x M x = .
1 1 2
2 2
2 1
1 2
x x
k
x x m

(
=
` `
(

) )

2 1
det 0
1 2

(
=
(


where
2
2
0

= and
2
0
k
m
=
( )
2
2
2 1 4 3 0 = + = , ( )( ) 3 1 0 = 1, 3 = .
1 0 2 0
, 3 3
k k
m m
= = = =
[Step 2] Find eigenvectors
Case (i)
0
=
m
m
k
2k
k
Multi-Degree of Freedom Systems
19
{ }
11 11
1
1
12 12
2 1 1 1 1 1
0 0
1 2 1 1 1 1



( (
= = =
` ` `
( (

) ) )

Normalization
1 1
1 0 1
1
1 0 1
T
m
m

(
=
` `
(
) )
.
2
1
1 1
1
1 1
T
m
| |

| =
` `
|
) )
\ .
.
2
1
2 1 m = .
Since
1
1
2m
= , ( )
1
1 2
1
1 2
m

=
`

)

Case (ii)
0
3 =
{ }
2
1 1
0
1 1

(
=
(


{ }
2
2
1
1


=
`

)

Normalization:
2 2
2 2
1 1
2 1
1 1
T
m m

= =
` `

) )
. Hence,
2
1
2m
=
{ }
2
1 2
1
1 2
m

| |
= |
|

\ .

[Step 3] Construct a Modal matrix [].
| | { } { }
1 2
1 1
1
,
1 1
2m

(
( = =
(




[Step 4] Solve the uncoupled differential equations.
( ) ( ) ( )
2 10
1 0 1 1 10 0 0
0
0 cos sin
z
z z z t z t t

+ = = +
`
``
( )
( ) ( )
2 20
2 0 2 2 20 0 0
0
3 0 cos 3 sin 3
z
z z z t z t t

+ = = +
`
``
| |
1
10 10
20 20
z x
z x

=
` `
) )
,
| |
1
10 10
20 20
z x
z x

=
` `
) )
` `
` `
or
( )
( )
( ) ( ) { }
( ) ( )
{ }
( ) ( )
( ) ( )
1
1 0 1 0 2 0 2 0
1 2
2
1 0 1 0 2 0 2 0
cos sin cos 3 sin 3
1 1
1 1
cos sin cos 3 sin 3
1 1
2 2
x t
t t t t
x t
t t t t
m m




(
= + + + (
`



)

(
= + + + (
` `



) )
Apply I.C.s
m
1
m
2
m
1
m
2
1
st
mode
2
nd
mode
Multi-Degree of Freedom Systems
20

10
1 2
20
10
0 0
1 2
20
1 1
1 1
2 2
1 1
3
1 1
2 2
x
x
m m
x
x
m m




+ =
` ` `

) ) )

+ =
` ` `

) ) )
`
`
Solve these equations to get
1
,
2
,
1
,
2
.

3.2. <Examples> : Three-degree of freedom system

Equation of motion
1 1 1 1 2 1 2 1
2 2 2 2 1 3 2 3 2
3 3 3 3 2 3
( ) ( )
( ) ( ) ( )
( ) ( )
m x k x k x x f t
m x k x x k x x f t
m x k x x f t
= +
= +
= +
``
``
``

Express the above equations in matrix forms.
1 1 1 2 2 1 1
2 2 2 2 3 3 2 2
3 3 3 3 3 3
0 0 0 ( )
0 0 ( )
0 0 0 ( )
m x k k k x f t
m x k k k k x f t
m x k k x f t
+ ( (

( (
+ + =
` ` `
( (

( (
) ) )
``
``
``
. (1)
Consider the case that m
1
= m
2
= m
3
= m, k
1
= k
2
= k
3
= k . Then, Eq. (1) becomes:
1 1 1
2 2 2
3 3 3
1 0 0 2 1 0 ( )
0 1 0 1 2 1 ( )
0 0 1 0 1 1 ( )
x x f t
m x k x f t
x x f t
( (

( (
+ =
` ` `
( (

( (
) ) )
``
``
``

Step I : solve the associated eigen-value problem.
2 2 2
2 1 0 1 0 0
[ ] [ ] 1 2 1 0 1 0 det [ ] [ ] 0
0 1 1 0 0 1
K M k m K M
( (
( (
( = =

( (
( (


Multi-Degree of Freedom Systems
21
2 1 0
det 1 2 1 0
0 1 1

(
(
=
(
(


2
(2 ) (1 ) (1 ) (2 ) 0 =
3 2
5 6 1 0 3.24698, 1.55496, 0.198062 + =
1
2 1 1
3
1.801938 1 0 0 0.554958
1 1.801938 1 0 { } 1.000
0 1 0.801938 0 1.24698
x
x
x

(

(
= =
` ` `
(

(
) ) )

1
2 2 2
3
0.44504 1 0 0 1.000
1 0.44504 1 0 { } 0.44504
0 1 0.55496 0 0.80193
x
x
x

(

(
= =
` ` `
(

(
) ) )

1
2 3 3
3
1.24698 1 0 0 1.000
1 1.24698 1 0 { } 1.24698
0 1 2.24698 0 0.55496
x
x
x

(

(
= =
` ` `
(

(
) ) )

Step II : Construct a normal matrix
| |
1 2 3
1 2 3 1 2 3
1 2 3
0.554958
[ ] { } { } { } 0.44504 1.24698
1.24698 0.80193 0.55496



(
(
= =
(
(


Since [ ] [ ][ ] [ ]
T
M I = ,
1 1
{ } [ ]{ } 1
T
M = , hence,
2 2 2 2 2
1 1
{ (0.554958 1.0000 1.24698 )} 2.862938 m m + + = .
1
0.59101
m
=
2 2 2
2 2 2
{ } [ ]{ } 1 { (1 0.44504 0.80193 )} 1
T
M m = + + =
2
0.736979
m
=
2 2 2
3 3 3
{ } [ ]{ } 1 { (1 1.24698 0.55496 )} 1
T
M m = + + =
3
0.591009
m
=
Therefore,
0.327986 0.736979 0.591009
1
[ ] 0.59101 0.327985 0.736976
0.73698 0.591006 0.327986
m
(
(
=
(
(

.
Multi-Degree of Freedom Systems
22

Step IV : Solve the uncoupled differential equations
2 2
1 0 1 1
0.44504 ( ) z z Q t + = `` where { ( )} [ ] { }
T
Q t f = .
Therefore,
1 11 1 21 2 31 3
( ) ( ) ( ) ( ) Q t f t f t f t = + + . i.e.,
1 1 1 2 3
( ) { } { } [0.327986 ( ) 0.59101 ( ) 0.73698 ( )] /
T
Q t f f t f t f t m = = + + .
2 2
2 0 2 2
1.24698 ( ) z z Q t + = `` where
2 2 1 2 3
( ) { } { } [0.736979 ( ) 0.327985 ( ) 0.591006 ( )] /
T
Q t f f t f t f t m = = +
2 2
3 0 3 3
1.80194 ( ) z z Q t + = `` where
3 3 1 2 3
( ) { } { } [0.591009 ( ) 0.736976 ( ) 0.327986 ( )] /
T
Q t f f t f t f t m = = + .


For the given initial conditions, x
1
(0) = x
2
(0) = x
3
(0) = 0,
1 2 3
(0) (0) (0) 0 x x x = = = ` ` ` ,
1 1 2 3 0
0
0
1 1
( ) [0.327986 ( ) 0.59101 ( ) 0.73698 ( )]sin[0.44504 ( )]
0.44504
t
z t f f f t d
m

= + +

2 1 2 3 0
0
0
1 1
( ) [0.736979 ( ) 0.327985 ( ) 0.591006 ( )]sin[1.24698 ( )]
1.24698
t
z t f f f t d
m

= +

3 1 2 3 0
0
0
1 1
( ) [0.591009 ( ) 0.736976 ( ) 0.327986 ( )]sin[1.80194 ( )]
1.80194
t
z t f f f t d
m

= +

Step V : Transform and obtain the solution
Since {x} = []{z} = z
1
(t){}
1
+ z
2
(t){}
2
+ z
3
(t){}
3
,
Multi-Degree of Freedom Systems
23
1
2 1 2 3 0
0
0
3
1 2 3
0
0
( ) 0.327986
1
( ) [0.327986 ( ) 0.59101 ( ) 0.73698 ( )]sin[0.44504 ( )] 0.59101
0.44504
( ) 0.73698
1
[0.736979 ( ) 0.327985 ( ) 0.591006 ( )]sin[1
1.24698
t
t
x t
x t f f f t d
m
x t
f f f
m

= + +
` `

) )
+ +

0
1 2 3 0
0
0
0.736979
.24698 ( )] 0.327985
0.591006
0.591009
1
[0.591009 ( ) 0.736976 ( ) 0.327986 ( )]sin[1.80194 ( )] 0.736976
1.80194
0.327986
t
t d
f f f t d
m

)


+ +
`

11 12 13
21 22 23 0
31 32 33
1
Let [ ] ,
i i
m



(
(
= =
(
(

. Then,
3
1 1 2 2 3 3
1
1 1
( ) [ ( ) ( ) ( )] ( )
i i i i ji j
j
Q t f t f t f t f t
m m

=
= + + =

. Hence,
3
0
0
1
0
1 1
( ) [ ( )]sin[ ( )]
t
i ji j i
j
i
z t f t d
m


=
=

and
3 3
0
0
0 1
0
1 1
{ ( )} ( ) sin[ ( )] { }
t
ji j i i
i j
i
x t f t d
m


= =
(

=
` (
)