Académique Documents
Professionnel Documents
Culture Documents
Additional Revision Questions Solutions
Transféré par
Nicholas TehDescription originale:
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Additional Revision Questions Solutions
Transféré par
Nicholas TehDroits d'auteur :
Formats disponibles
Additional Revision Questions Solutions
1(a) In general,
th
n bracket contains n terms
sum of number of term in nbrackets ) 1 (
2
........ 3 2 1 + = + + + + = n
n
n (shown)
(b) Sum of integers in nbrackets
] 2 ) 1 ( 4 )[ 1 (
4
) 2 ( 1 ) 1 (
2
) 2 ( 2 ) 1 (
2 2
1
+ + + =
)
`
+ +
(
+ = n n n
n
n
n
n
n
( ) 2 ) 1 (
4
2
+ + + = n n n
n
(shown)
(c) Total number of terms in ( ) 1 n brackets ) (
2
1
) 1 1 (
2
1
n
n
n
n
= +
=
Last term in
th
n ) 1 ( bracket n n n n n
n
= + =
(
+ =
2
2 ) )( 1 ( 2 ) 2 ( 1 ) (
2
1
2
First term in
th
n bracket 2
2
+ = n n (shown)
Sum of integers in
th
n bracket ( ) | | ) 1 )( ( ) 2 )( 1 ( 2 2
2
2 2
+ = + + = n n n n n
n
(shown)
2 (i)
12
1
3
2
1
3
2
12
1 1
<
|
\
|
<
|
\
|
n n
Solving gives 205 . 7 > n , minimum value of 8 = n (shown)
(ii) ( ) ( ) ( )
(
(
+ |
\
|
+ |
\
|
+ =
=
........ ..........
3
2
12
3
2
12 12
4
2
2
2 2
1
i
i
A
5
1296
3
2
1
12
2
2
=
(
(
(
(
(
\
|
= (shown)
3. Let the proposition
n
P be ( )
1
1
2 2 ) 1 (
+
=
= +
n
n
r
r
n r , where
+
n
Considering :
1
P LHS 4 ) 2 )( 1 1 ( = + = and 4 ) 2 )( 1 (
2
= ; since LHS=RHS,
1
P is true.
Assume
k
P is true for some ,
+
k ie ( )
1
1
2 2 ) 1 (
+
=
= +
k
k
r
r
k r
For :
1 + k
P ( )
1 1 1
1
1
1
2 ) 2 ( 2 2 ) 2 ( 2 ) 1 ( 2 ) 1 (
+ + +
=
+
=
+ + = + + + = +
k k k
k
r
r
k
r
r
k k k r r
) 1 ( 2 ) 2 2 ( 2 ) 2 ( 2
2 1 1
+ = + = + + =
+ + +
k k k k
k k k
k
P is true is
1 + k
P true. Since
1
P is true, by Mathematical Induction,
( )
1
1
2 2 ) 1 (
+
=
= +
n
n
r
r
n r for all
+
n (shown)
4. =
+
+
=
= =
1
1 1 1
1 1
r r e
e
U
N
r
r
N
r
r
1
1
e
e
2
1
1+
2
1
e
e
3
1
2
1
+
3
1
e
e
4
1
3
1
+
N
e
e 1
1
1 1
+
+
N N
1
1
1
1
..........
1 1 1
) 1 (
3 2
+
+
(
+ + + =
N e e e e
e
N
1
1
1
1
1
1
1
1
) 1 (
+
+
(
(
(
(
(
|
|
\
|
|
\
|
|
\
|
=
N
e
e e
e
N
1
1
1
1
1 1
) 1 (
+
+
(
(
(
(
(
|
|
\
|
|
\
|
=
N
e
e
e
e
e
e
N
N
1
1
1
1
+
+
=
N e
e
N
N
1
1
1 1
+
+ =
N
e
N
N
e
N
+
=
1
1
(shown)
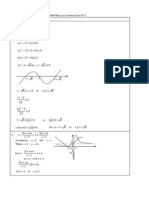
From the graph on the left, it is observed that
1
1
1
+ N
(bolded curve)
N
e
N
>
+
=
1
1
for all 0 > N
N
e
Hence, 0 >
N
S (shown)
5(i) y y
x x x f 2 ) (
2
+ = | 4 | ) ( + = x x g
4
1 0 x
4 0 x
1
, 0 [ =
g
R ); for
1
f to exist, largest possible domains for f are 1 x or 1 x .
However, since ) (x fg DOES NOT exist, ie
f g
D R , 1 x is rejected and the
largest domain satisfying all conditions is 1 x . (shown)
(ii) ( )
2 2
2 | 4 2 | ) ( + = + + = x x x x gf
For , 12 ) ( > x gf ( ) > + 12 2
2
x 0 ) 2 )( 4 ( 0 8 2
2
> + > + x x x x
4 < x or 2 > x (shown)
6(a) k f f = = ) 0 ( ) 2 ( , hence f is not one-one. (shown)
y From the graph on the left, it can be
seen that the largest possible
) (x f domain for
1
f to exist is , ( 1]
1 k where 1 = (shown)
0 1 x
When f and
1
f intersect, x k x x x x f = + = 2 ) (
2
Substituting
2
1
= x gives
4
7
2
1
2
1
3 3
2
2
=
|
\
|
|
\
|
= = x x k (shown)
(b) ,
2 1 2 1
) (
2
2
x x x x
x gh =
|
\
|
= 1 x (shown)
( ) , 0 ( , =
h g
R D 1] , 0 ( = 1]
Substituting this new domain , 0 ( = 1] into g gives , 1 [ =
gh
R ) 0 (shown)
7. Let the proposition
n
P be
=
+ =
n
r
n n n r r
1
), 1 4 )( 1 (
6
1
) 1 2 ( , where
+
n
Considering :
1
P LHS=( ) , 1 ) 1 2 ( 1 = RHS= ; 1 ) 3 )( 2 )( 1 (
6
1
= since LHS=RHS,
1
P is true.
Assume
k
P is true for some ,
+
k ie
=
+ =
k
r
k k k r r
1
) 1 4 )( 1 (
6
1
) 1 2 (
For :
1 + k
P | |
+
= =
+ + + =
1
1 1
1 ) 1 ( 2 ) 1 ( ) 1 2 ( ) 1 2 (
k
r
k
r
k k r r r r
) 1 2 )( 1 ( ) 1 4 )( 1 (
6
1
+ + + + = k k k k k )] 1 2 ( 6 ) 1 4 ( )[ 1 (
6
1
+ + + = k k k k
( ) ) 3 4 )( 2 )( 1 (
6
1
6 11 4 ) 1 (
6
1
2
+ + + = + + + = k k k k k k
| || | 1 ) 1 ( 4 1 ) 1 ( ) 1 (
6
1
+ + + + = k k k
k
P is true is
1 + k
P true. Since, by Mathematical Induction,
=
+ =
k
r
k k k r r
1
) 1 4 )( 1 (
6
1
) 1 2 ( for all
+
k (shown)
th
r term of series
) 2 )( 1 2 ( )] 2 )( 1 ( 2 )][ 2 )( 1 ( 1 [ r r r r = + + =
= =
= = + + +
n
r
n
r
r r r r
1 1
) )( 1 2 ( 2 ) 2 )( 1 2 ( ..... .......... ) 6 )( 5 ( ) 4 )( 3 ( ) 2 )( 1 (
) 1 4 )( 1 (
3
1
) 1 4 )( 1 (
6
1
2 + =
(
+ = n n n n n n (shown)
8. ( )
=
+
=
+
sec sec
tan 1
1
1
1
2
2 2
d dx
x
d
( ) C x x C + + = + + =
1
tan sec ln | tan sec | ln (shown)
y
(i) 1 x y
3 2
1
=
R
2
1
1
1
2
+
=
x
y
0 3 x
(ii) Area of R ( ) | |
4
3
tan sec ln
2
3
2
1
2
1
1
1
3
0
1
3
0
2
+ =
|
|
\
|
|
\
|
+
=
x x dx
x
4
3
) 3 2 ln( + = sq units (shown)
(iii)
+ = |
\
|
=
3
0
2
2
3
0
4
1
2
1
y y dx y V
+
+
+
=
3
0
2
2
4
1
1
1
1
1
dx
x
x
dx
( )
(
+ + =
(
+ + =
4
3
) 3 2 ln(
3 4
1
tan sec ln tan
3
0
1 1
x x x x
513 . 0 = cubic units (shown)
9 (a) ( ) 3 10 2 5 ) 1 ( 2 ) 1 ( 5
2 2
1
+ = + + = =
+
n n n n n u u T
n n n
10 ] 3 ) 1 ( 10 [ ) 3 10 (
1
= + + =
n n T T
n n
The difference between consecutive terms of the sequence forms an AP. (shown)
| | 12900 ) 10 )( 1 50 ( ) 13 ( 2
2
50
50
= + = S (shown)
(b) (i) After 1
st
operation, volume extracted ) 50 ( 05 . 0 =
volume left ) 50 ( 95 . 0 ) 50 ( 05 . 0 50 = =
After 2
nd
operation, volume extracted ( ) ) 50 ( 95 . 0 05 . 0 =
total volume extracted ( ) ) 50 ( 95 . 0 05 . 0 ) 50 ( 05 . 0 + =
( )
95 . 0 1
95 . 0 1 ) 50 ( 05 . 0
] 95 . 0 1 )[ 50 ( 05 . 0
2
= + =
( )
2
95 . 0 1 50 =
volume left ( ) ( )
2 2
95 . 0 50 95 . 0 1 50 50 = =
After 3
rd
operation, volume extracted ( )( )
2
95 . 0 50 05 . 0 =
total volume extracted ( ) ( )( )
2
95 . 0 50 05 . 0 ) 50 ( 95 . 0 05 . 0 ) 50 ( 05 . 0 + + =
( )
95 . 0 1
95 . 0 1 ) 50 ( 05 . 0
] 95 . 0 95 . 0 1 )[ 50 ( 05 . 0
3
2
= + + =
( )
3
95 . 0 1 50 =
Hence, after noperations, total volume extracted ( )
n
95 . 0 1 50 = (shown)
(ii) Total volume = > 25 ) 5 . 0 ( 50 ( ) 25 95 . 0 1 50 >
n
> 5 . 13 n least value of 14 = n (shown)
It is not possible to extract all the air in the bottle unless an infinite (unattainable) number of
operations have been carried out. (shown)
10 (i) ,
4
3
1
= u ,
36
5
2
= u ,
144
7
3
= u
400
9
4
= u
,
4
3
1
=
=
n
r
r
u ,
9
8
25
24
,
16
15
for , 1 = n 2 , 3 and 4 respectively (shown)
(ii)
= = =
+
=
+
+
=
n
r
n
r
n
r
r
r r r r
r
u
1
2 2
1
2 2
1
) 1 (
1 1
) 1 (
1 2
=
4
1
1
2
) 1 (
1
1
+
=
n
(shown)
9
1
4
1
16
1
9
1
2 2
) 1 (
1 1
+
n n
(iii) Let the proposition
n
P be
2
1
2 2
) 1 (
1
1
) 1 (
1 2
+
=
+
+
=
n r r
r
n
r
, where
+
n
Considering :
1
P LHS= ,
4
3
) 1 1 (
1 2
2
=
+
+
RHS= ;
4
3
4
1
1 = since LHS=RHS,
1
P is true.
Assume
k
P is true for some ,
+
k ie
2
1
2 2
) 1 (
1
1
) 1 (
1 2
+
=
+
+
=
k r r
r
k
r
For :
1 + k
P
2 2
1
2 2
1
1
2 2
) 2 ( ) 1 (
1 ) 1 ( 2
) 1 (
1 2
) 1 (
1 2
+ +
+ +
+
+
+
=
+
+
=
+
=
k k
k
r r
r
r r
r
k
r
k
r
2 2 2
) 1 (
1
1
) 2 ( ) 1 (
1 ) 1 ( 2
+
+
+ +
+ +
=
k k k
k
(
+
+
+
=
2 2
) 2 (
3 2
1
) 1 (
1
1
k
k
k
(
+
+
+
=
(
+
+
+
=
2
2
2 2
2
2
) 2 (
) 1 (
) 1 (
1
1
) 2 (
3 2 ) 2 (
) 1 (
1
1
k
k
k k
k k
k
2
) 2 (
1
1
+
=
k
k
P is true is
1 + k
P true. Since
1
P is true, by Mathematical Induction,
2
1
2 2
) 1 (
1
1
) 1 (
1 2
+
=
+
+
=
n r r
r
n
r
for all
+
n (shown)
2 2
2
1
1
1
1
3
1
9
1
9
8
) 1 1 (
1
1
n n
u u u
r
r
n
r
r
n
r
r
=
+
= =
=
=
(shown)
(iv) 1
1
1
=
= r
r
u (shown)
11(i) Vector normal to
2
is
|
|
|
\
|
0
0
1
4
0
0
1
0
1
4
0
0
1
=
|
|
|
\
|
|
|
|
\
|
=
|
|
|
\
|
r and Cartesian equation of
2
is 4 = x (shown)
(ii) For ,
1
; 2 2
1
0
0
5 = =
|
|
|
\
|
|
|
|
\
|
b
b
a
for
2
, 4 4
0
0
1
5 = =
|
|
|
\
|
|
|
|
\
|
a
b
a
(shown)
Direction vector of line of intersection
|
|
|
\
|
=
|
|
|
\
|
|
|
|
\
|
=
0
1
0
0
0
1
1
0
0
Equation of line of intersection is
|
|
|
\
|
+
|
|
|
\
|
=
0
1
0
2
5
4
r (shown)
(iii)
|
|
|
\
|
=
|
|
|
\
|
|
|
|
\
|
=
4
0
8
2
5
4
6
5
4
PQ
Since , 0
0
1
0
=
|
|
|
\
|
PQ point Qis directly above point P foot of perpendicular from Q
to line l
|
|
|
\
|
= =
2
5
4
OP (shown)
(iv)
Q
d
|
|
|
\
|
=
1
0
0
n
P
Shortest distance from Qto 4
1
= =
n PQ
units(shown)
5
1
80
4
4
0
8
4
sin = =
|
|
|
\
|
= (shown)
12(i) For point , A ; 4
2
0
1
0
0
4
=
|
|
|
\
|
|
|
|
\
|
=
For point , P 4 1
2
0
1
1
1
=
|
|
|
\
|
|
|
|
\
|
=
Point Alies on
1
but point P does not. (shown)
(ii) P
|
|
|
\
|
1
1
|
|
|
\
|
2
0
1
A
|
|
|
\
|
0
0
4
N
(
(
(
(
|
|
|
\
|
=
2
0
1
AP NP
|
|
|
\
|
2
0
1
|
|
|
\
|
=
|
|
|
\
|
(
(
(
|
|
|
\
|
|
|
|
\
|
=
2
0
1
2
0
1
5
1
2
0
1
5
1
1
3
= = + = NP OP ON NP ON OP
|
|
|
\
|
=
|
|
|
\
|
|
|
|
\
|
1
2
2
0
1
1
1
(shown)
(iii) For ,
2
= = AN AP n
2
|
|
|
\
|
=
(
(
(
|
|
|
\
|
|
|
|
\
|
|
|
|
\
|
5
2
0
0
4
1
2
1
3
|
|
|
\
|
5
2
Equation of
2
is
8 5
2
0
0
4
5
2
=
|
|
|
\
|
|
|
|
\
|
=
|
|
|
\
|
r (shown)
Line of intersection of
1
and
2
has the direction vector
|
|
|
\
|
=
1
2
AN
Equation of line of intersection is
|
|
|
\
|
+
|
|
|
\
|
=
1
2
0
0
4
r (shown)
(iv) If all 3 planes intersect in a line, then for ,
3
direction vector of l (ie line of intersection of
1
and
2
) must be perpendicular to .
3
n
Hence, 4 0
2
1
1
1
2
= =
|
|
|
\
|
|
|
|
\
|
(shown)
(v) The augmented matrix when 2 = is given by
|
|
|
\
|
4 2 1 1
16 2 5 4
4 2 0 1
Solving this gives the common point of intersection
|
|
|
\
|
=
0
0
4
(shown)
13.
( )( )
( )
, 1
5
2
2 5
|
\
|
= = =
k
i
k i
e w e w , 0 = k , 1 2
( ) ( ) ( ) ( ) |
\
|
|
\
|
|
\
|
|
\
|
=
5
4
5
4
5
2
5
2
, , , , 1
i i i i
e e e e w (shown)
(i)
( ) ( ) ( ) ( )
) (
2
sin 2 1
2 2 2 2
i e e e e e
i i i i
i
|
\
|
=
(
(
=
|
\
|
|
\
|
|
\
|
|
\
|
(shown)
(ii) Let
( )
( )
2
cos
2
1
) (
2
sin 2
1
1
1
1
1 1
2
2
ec ie
i e
e w
z
z
z
w
i
i
i
|
\
|
\
|
=
|
\
|
=
=
+
=
( )
2
cot
2 2
1
2
cos
2
sin
2
cos
2
1 i
ec i i =
(
=
|
\
|
=
2
cot 1
2
1
i where ,
5
2
=
5
4
The roots are given by
|
\
|
5
cot 1
2
1
i and
|
\
|
5
2
cot 1
2
1
i (shown)
14. (a) Let wbe the root(s) of the equation
|
\
|
+
= + =
6
2 ) (
3
2
1
2
3
k i
e i w ,
ie
|
\
|
+
=
18 3
2
) (
k
i
e w where , 0 = k 1, 2
Hence,
( ) ( ) ( ) |
\
|
|
\
|
|
\
|
=
18
13
18
11
18
, ,
i i i
e e e w (shown)
0 3 1 0 1
3 1
6 3
3 6
= + = + z z
z z
i z
2
1
2
3
2
4 3 3
3
=
=
and
( ) ( ) ( ) |
\
|
|
\
|
|
\
|
=
18
13
18
11
18
, ,
i i i
e e e z (shown)
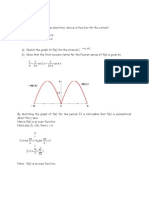
(b) Im
Locus of ) (w Q
i 2 Locus of ) (z P
k
0 3 Re
6 units
1
w
i 4
6
From the above Argand Diagram, observing the right angle triangle, 3
6 6
sin = = k
k
(shown)
(i) Maximum value of 6
1
= w w (shown)
(ii)
6
Range is
3
2
) 4 3 arg(
3
+ i w (shown)
15(a)
( )
C
x
x
C
x
x
dx
x
dx
x
+
+
= +
+
|
\
|
=
2 3
2 3
ln
8
1
2 3
2 3
ln
4
1
2
1
2 3
2
2
1
4 9
1
2 2 2
(shown)
(b)
x
2
cos x x dx
x
dx 2 sin
4
1
2
1
2
2 cos 1
+ =
+
=
(shown)
(i) Let , 2 x y = then ( )
=
3
2
0
2
3
0
2
cos
2
1
2 cos
x dy y dx
16
3
6
2 sin
4
1
2
1
2
1
3
2
0
=
(
+ =
x x (shown)
(ii) ( )
+
(
\
|
+ =
3
0
3
0
3
0
2
2 sin
4
1
2
1
) ( 2 sin
4
1
2
1
cos
x x x x x dx x x dx
3
0
2
2 cos
8
1
4
1
8
3
6 3
|
|
\
|
+ = x x
16
3
3 8
36 8
1
16
1
36
3 8
18
2 2 2
+ =
(
+
|
|
\
|
+ + =
(shown)
16(i)
( )
( )
( )
( )
C
x
C
x
dx x x dx
x
x
+
+
= +
+
= + =
+
7
2
7
2
8
2
8
2
5 2 28
1
) 7 (
5 2
4
1
5 2 ) (
4
1
5 2
(shown)
(ii)
=
=
+
dx
x
e
dx
x
e
dx
x x
e
x x x
2
tan
2
tan tan
cos sin 1 ) sin 1 )( sin 1 (
( ) C e dx e x
x x
+ = =
tan tan 2
sec (shown)
(iii) ( )
=
|
\
|
\
|
= dx xe e x dx e x x e dx e x
x x x x x 3 3 2 3 2 3 3 2
3
2
3
1
3
1
) 2 (
3
1
C e xe e x dx e xe e x
x x x x x x
+ + =
(
=
3 3 3 2 3 3 3 2
27
2
9
2
3
1
3
1
3
1
3
2
3
1
(shown)
17 (i)
( ) ( )( )
( )( )
2
3 2 2 2
2
1
1
1 1
1 1
1
1
1
1
1
1
e
e
e e
e e e
e
e e
e
e e
e
e
e u
=
+
+ +
=
+
+ +
=
+
+
=
+
+ =
3
4
3
2
3
1
1
1
1
1
e
e
e
e
e e u
=
|
|
\
|
+ = Conjecture is
n
n
n
e
e
u
=
+
1
1
1
(shown)
(ii) Let the proposition
n
P be
n
n
n
e
e
u
=
+
1
1
1
, where
+
n
Considering :
1
P , 1
1
) 1 )( 1 (
1
1
2
1
e
e
e e
e
e
u + =
+
=
= hence
1
P is true.
Assume
k
P is true for some ,
+
k ie
k
k
k
e
e
u
=
+
1
1
1
For :
1 + k
P
|
|
\
|
+ = + =
+
+
1
1
1
1
1 1
k
k
k
k
e
e
e e
u
e
e u
( )( )
1
2
1
1 1
1
1
1
1 1
+
+
+
+ +
+ +
=
k
k
k
k k
e
e
e
e e e e
k
P is true is
1 + k
P true. Since
1
P is true, by Mathematical Induction,
n
n
n
e
e
u
=
+
1
1
1
for all
+
n (shown)
(iii) When , n e
e
e
e
e
u
n
n
n
n
n
=
=
+ + 1 1
1
1
(shown)
18.
( )
= =
+
=
+
=
+ + +
+ +
+ +
+
+
+
n
r
n
r
r r
r
r
n
1 1
) 1 (
2
1
2
1
......... 2 1
1
.........
3 2 1
1
2 1
1
1
1
(shown)
Let the proposition
n
P be
1
1
1
......... 2 1
1
.........
3 2 1
1
2 1
1
1
1
2
1
+
=
|
\
|
+ + +
+ +
+ +
+
+
+
n n
,
ie
1
1
1
) 1 (
1
) 1 (
2
2
1
1 1
+
=
+
=
+
= =
n r r r r
n
r
n
r
where
+
n
Considering :
1
P LHS= ,
2
1
) 1 1 )( 1 (
1
=
+
RHS= ;
2
1
1 1
1
1 =
+
since LHS=RHS,
1
P is true.
Assume
k
P is true for some ,
+
k ie
1
1
1
) 1 (
1
1
+
=
+
=
k r r
k
r
For :
1 + k
P
) 2 )( 1 (
1
1
1
1
) 2 )( 1 (
1
) 1 (
1
) 1 (
1
1
1
1
+ +
+
+
=
+ +
+
+
=
+
=
+
=
k k k k k r r r r
k
r
k
r
2
1
1
2
1
1
1
1
2
1
1
1
1
1
+
=
|
\
|
+
+
+
=
|
\
|
+
+
=
k k
k
k k k
k
P is true is
1 + k
P true. Since
1
P is true, by Mathematical Induction,
1
1
1
) 1 (
1
1
+
=
+
=
n r r
n
r
for all
+
n (shown)
1
) 1 (
1
1
=
+
= r
r r
(shown)
19 (i)
A 4 P 1 B
|
|
|
\
|
=
(
(
(
|
|
|
\
|
+
|
|
|
\
|
=
+
=
1
2
3
3
2
5
2
2
5
4
5
1
5
4 OA OB
OP (shown)
(ii) Both
1
and contain the direction vector
|
|
|
\
|
3
2
7
as well as points Aand B .
[ Since
1
contains the line l , then it also contains the point A; since P also lies on ,
1
in addition the chords AP and PB must exist as a continuous line, therefore B also lies on .]
1
Hence, vector equation of line of intersection is
|
|
|
\
|
+
|
|
|
\
|
=
3
2
7
2
2
5
r (shown)
Another direction vector lying on
|
|
|
\
|
=
|
|
|
\
|
|
|
|
\
|
= =
4
0
8
3
2
5
1
2
3
1
AP
|
|
|
\
|
1
0
2
|
|
|
\
|
=
|
|
|
\
|
|
|
|
\
|
=
4
1
2
3
2
7
1
0
2
1
n and equation of :
1
0
4
1
2
1
2
3
4
1
2
=
|
|
|
\
|
|
|
|
\
|
=
|
|
|
\
|
r (shown)
Let angle between planes
1
and be
Then n n n =
1
cos
1
n
|
|
|
\
|
=
|
|
|
\
|
|
|
|
\
|
11
34
5
4
1
2
11
34
5
cos
4
1
2
|
|
|
\
|
Solving , 0 cos = ie
o
90 = (shown)
(upright)
Line l
B 1
1
P
4
A
2
d
1
d
Required ratio 1 : 4 cos : cos 4 :
2 1
= = = d d (shown)
20 (i) 4
2
1
2
2 1
2 2 =
|
|
|
\
|
|
|
|
\
|
1
l lies on
1
(shown)
(ii)
|
|
|
\
|
=
|
|
|
\
|
|
|
|
\
|
=
3
6
6
2
2
1
2
1
2
2
n
|
|
|
\
|
1
2
2
and equation of :
2
5
1
2
2
1
2
0
1
2
2
=
|
|
|
\
|
|
|
|
\
|
=
|
|
|
\
|
r (shown)
(iii) Equation of :
3
0
1
1
1
=
|
|
|
\
|
r (shown)
(iv) Equation of :
4
4
1
0
1
=
|
|
|
\
|
r
Augmented matrix is given by
|
|
|
\
|
4 1 0 1
0 1 1 1
4 2 1 2
which is reduced to
|
|
|
\
|
0 0 0 0
4 0 1 0
4 1 0 1
Let , = z then line of intersection is given by
|
|
|
\
|
+
|
|
|
\
|
=
|
|
|
\
|
=
|
|
|
\
|
=
1
0
1
0
4
4
4
4
z
y
x
r
(shown)
21 (a) Using the identity
|
\
|
|
\
| +
=
2
sin
2
sin 2 cos cos
B A B A
B A , we have
( )
4 cos 10 cos
2
1
3 sin 7 sin
2
2
= =
d
x d
Integrating both sides wrt ,
C
d
dx
+ + =
4 sin
8
1
10 sin
20
1
When , 0 = 0 0 = = C
d
dx
Integrating both sides once again wrt ,
B x + = 4 cos
32
1
10 cos
200
1
When , 0 =
800
21
0 = = B x ; hence
800
21
4 cos
32
1
10 cos
200
1
+ = x (shown)
When , 0 = x , 42 . 1 = , 72 . 1 14 . 3 (shown)
(b) (i) Differentiating both sides of
y
xe z = wrt x gives
( ) ) (x e
dx
dy
e
dx
dz
y y
+ = ; substituting into (1) as defined in the question gives x
dx
dz
2 = (shown)
(ii) Integrating both sides of x
dx
dz
2 = wrt : x k x xe k x z
y
+ = + =
2 2
x
k
x e
y
+ =
|
\
|
+ =
x
k
x y ln
(shown)
(iii)
y
|
\
|
=
x
x y
1
ln
1 0 1 1.62 x
618 . 0
Vous aimerez peut-être aussi
- Tenth Dimension Ebook PDFDocument227 pagesTenth Dimension Ebook PDFshit-_happens100% (5)
- 2008 h2 Math Prelim p1 (Solns)Document19 pages2008 h2 Math Prelim p1 (Solns)Utsav NiroulaPas encore d'évaluation
- ACJC 2014 H2 Maths Supp Exam (Solution For Students)Document9 pagesACJC 2014 H2 Maths Supp Exam (Solution For Students)RaymondZhangPas encore d'évaluation
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document10 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongPas encore d'évaluation
- F.H. Parker - A Demonstration of Epistemological RealismDocument27 pagesF.H. Parker - A Demonstration of Epistemological RealismdaPipernoPas encore d'évaluation
- Tree NotesDocument67 pagesTree NotesRahul RawatPas encore d'évaluation
- Homework #3, Sec 10.3Document6 pagesHomework #3, Sec 10.3Masaya Sato100% (8)
- Interpreting Graphs LessonDocument5 pagesInterpreting Graphs LessonChristina AlexanderPas encore d'évaluation
- AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document12 pagesAJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongPas encore d'évaluation
- 2014 2 JOHOR SMKTinggiKluang Maths QADocument8 pages2014 2 JOHOR SMKTinggiKluang Maths QASK100% (2)
- Additional Calculus Problems 2-Integration and Applications SolutionsDocument5 pagesAdditional Calculus Problems 2-Integration and Applications SolutionsNicholas TehPas encore d'évaluation
- HCI 2008 Promo W SolutionDocument12 pagesHCI 2008 Promo W SolutionMichael CheePas encore d'évaluation
- Additional Calculus Problems - Integrations and Applications SolutionsDocument4 pagesAdditional Calculus Problems - Integrations and Applications SolutionsNicholas TehPas encore d'évaluation
- Anggota KelompokDocument36 pagesAnggota Kelompokanon_267791969Pas encore d'évaluation
- 2011 Set B Mock Paper 1 SolutionsDocument15 pages2011 Set B Mock Paper 1 SolutionsJordan TiongPas encore d'évaluation
- Digital Assignment 1: B1 + TB1 Statistics For Engineers (Mat-2001) Prof. Kalaivani KDocument9 pagesDigital Assignment 1: B1 + TB1 Statistics For Engineers (Mat-2001) Prof. Kalaivani KHappy AsiamPas encore d'évaluation
- Jawaban 5.2Document7 pagesJawaban 5.2Nanda SafiraPas encore d'évaluation
- 2010 DHS Paper 1solDocument10 pages2010 DHS Paper 1solnothingtodo1992Pas encore d'évaluation
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document22 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongPas encore d'évaluation
- 18th March Shift-1 Mathematics (Crackjee - Xyz)Document12 pages18th March Shift-1 Mathematics (Crackjee - Xyz)StockPlusIndiaPas encore d'évaluation
- Musune Complex AssignDocument10 pagesMusune Complex AssignMakani MusunePas encore d'évaluation
- Functions, Limits & Continuity DifferentiationDocument5 pagesFunctions, Limits & Continuity DifferentiationSharath Aefdsffdf FdPas encore d'évaluation
- A-Level H2 Maths 2010 - Paper 2: Mathematics (Higher 2) 9740/02Document11 pagesA-Level H2 Maths 2010 - Paper 2: Mathematics (Higher 2) 9740/02Lawrence Lim Ah KowPas encore d'évaluation
- Week7 CHAPTER 1: Laplace Transform MAT485/565: (N) N n-1 n-2 (2) (n-1)Document4 pagesWeek7 CHAPTER 1: Laplace Transform MAT485/565: (N) N n-1 n-2 (2) (n-1)qistinaPas encore d'évaluation
- Logaritmos - Ejercicios 2Document1 pageLogaritmos - Ejercicios 2Christian Ricardo Calderon SorianoPas encore d'évaluation
- Hector Daniel Castro Perez - 100410 - 100Document9 pagesHector Daniel Castro Perez - 100410 - 100Hector Daniel Castro PerezPas encore d'évaluation
- Exercise5 PDFDocument3 pagesExercise5 PDFRaveenaPas encore d'évaluation
- H2 9740 2010 Paper 2 SolutionDocument7 pagesH2 9740 2010 Paper 2 SolutionqeemengPas encore d'évaluation
- 2007 Ajc h2 Prelims Paper 1 SolutionsDocument9 pages2007 Ajc h2 Prelims Paper 1 Solutionsvincesee85Pas encore d'évaluation
- Ath em Ati CS: L.K .SH Arm ADocument10 pagesAth em Ati CS: L.K .SH Arm APremPas encore d'évaluation
- DHS 2021 H2 Math JC1 Mid-Year Exam (Sol)Document10 pagesDHS 2021 H2 Math JC1 Mid-Year Exam (Sol)Sim Jun Ming Reeve (Sajc)Pas encore d'évaluation
- Penang JitSin MathsT P1 2015 QADocument13 pagesPenang JitSin MathsT P1 2015 QAlingbooPas encore d'évaluation
- Tutorial-05 (Answers)Document9 pagesTutorial-05 (Answers)lahirudb1Pas encore d'évaluation
- Answers-Chaks Pure Maths P2 Ex 1 Pure Mathematics0001Document13 pagesAnswers-Chaks Pure Maths P2 Ex 1 Pure Mathematics0001Michael MyamboPas encore d'évaluation
- Sección 1.3 y 1.4Document5 pagesSección 1.3 y 1.4juancho 507Pas encore d'évaluation
- Skema Add Math Melaka K2 2023Document9 pagesSkema Add Math Melaka K2 2023HASWIN EDU HUBPas encore d'évaluation
- AP EAMCET 2019 Previous Year Question Papers With Solutions - 20th April 2019 Evening ShiftDocument220 pagesAP EAMCET 2019 Previous Year Question Papers With Solutions - 20th April 2019 Evening Shiftyashwanthkumarmannava18Pas encore d'évaluation
- AP EAMCET 2018 Previous Year Question Papers With Solutions - 23rd April 2018 Evening ShiftDocument195 pagesAP EAMCET 2018 Previous Year Question Papers With Solutions - 23rd April 2018 Evening Shiftyashwanthkumarmannava18Pas encore d'évaluation
- ST Paul 2019 Answer P1Document7 pagesST Paul 2019 Answer P1g-22255924Pas encore d'évaluation
- Answers Paper AIEEEDocument17 pagesAnswers Paper AIEEESuyash ChauhanPas encore d'évaluation
- Actividad 2 Sumas de RiemannDocument7 pagesActividad 2 Sumas de RiemannFlakita VianethPas encore d'évaluation
- Rvhs h2 Math p1 SolutionsDocument13 pagesRvhs h2 Math p1 SolutionsjimmytanlimlongPas encore d'évaluation
- 2020 Nov PPR 2 Suggested Marking Guide by TrockersDocument29 pages2020 Nov PPR 2 Suggested Marking Guide by TrockersPriscaPas encore d'évaluation
- 2010 Set B Paper 3 RVHS Promo (Solutions)Document12 pages2010 Set B Paper 3 RVHS Promo (Solutions)Lim Kew ChongPas encore d'évaluation
- JEE Main 2021 March 18 Question Paper With Solutions by R - dxUKhGJDocument69 pagesJEE Main 2021 March 18 Question Paper With Solutions by R - dxUKhGJhari kishorePas encore d'évaluation
- 2010-H2 Maths-Integration and Its Applications (Tut 3) - Int Applications Solutions)Document13 pages2010-H2 Maths-Integration and Its Applications (Tut 3) - Int Applications Solutions)Anita Yun Chu PengPas encore d'évaluation
- Maths 1Document22 pagesMaths 1ramkumarashvanth09Pas encore d'évaluation
- Vidyalankar Vidyalankar Vidyalankar Vidyalankar: Advanced Engineering MathematicsDocument16 pagesVidyalankar Vidyalankar Vidyalankar Vidyalankar: Advanced Engineering MathematicsPooja JainPas encore d'évaluation
- 2024 Live 22 MarkingDocument7 pages2024 Live 22 Markingcodavenger596Pas encore d'évaluation
- 2006 AJC H2 MY SolnDocument9 pages2006 AJC H2 MY Solnjunie9201Pas encore d'évaluation
- Class - XII: Mathematics (041) SQP Marking Scheme (2019-20)Document13 pagesClass - XII: Mathematics (041) SQP Marking Scheme (2019-20)ganesh kumarPas encore d'évaluation
- Be Computer-Engineering Semester-4 2018 May Applied-Mathematics-Iv-CbcgsDocument19 pagesBe Computer-Engineering Semester-4 2018 May Applied-Mathematics-Iv-Cbcgsminji kunPas encore d'évaluation
- JEE Main 2021 18 March Shift 1 MathDocument17 pagesJEE Main 2021 18 March Shift 1 MathmedhaPas encore d'évaluation
- A-4 Lunes 29-06-2022 - 29-06-2022Document17 pagesA-4 Lunes 29-06-2022 - 29-06-2022Alexander Zapata SequeirosPas encore d'évaluation
- Mathematics Sample Paper Solutions Section-ADocument19 pagesMathematics Sample Paper Solutions Section-APoonamBhardwajPas encore d'évaluation
- Material Informativo 2Document8 pagesMaterial Informativo 2marco andonairePas encore d'évaluation
- Solution IYMC Qualification Round 2020Document3 pagesSolution IYMC Qualification Round 202072 Tanvir AhmedPas encore d'évaluation
- Revision FourierDocument19 pagesRevision FourierHazim NaharPas encore d'évaluation
- Paper B SolutionDocument11 pagesPaper B SolutiontimchanymPas encore d'évaluation
- Nios Math 2018Document9 pagesNios Math 2018Vineet KumarPas encore d'évaluation
- Seminar 4Document3 pagesSeminar 4Б. ДөлгөөнPas encore d'évaluation
- Ten-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesD'EverandTen-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesPas encore d'évaluation
- Answers to Selected Problems in Multivariable Calculus with Linear Algebra and SeriesD'EverandAnswers to Selected Problems in Multivariable Calculus with Linear Algebra and SeriesÉvaluation : 1.5 sur 5 étoiles1.5/5 (2)
- Analytic Geometry: Graphic Solutions Using Matlab LanguageD'EverandAnalytic Geometry: Graphic Solutions Using Matlab LanguagePas encore d'évaluation
- 12 Gold 4 - C2 Edexcel PDFDocument17 pages12 Gold 4 - C2 Edexcel PDFNicholas TehPas encore d'évaluation
- Arithmetic ISF Notes DLDocument2 pagesArithmetic ISF Notes DLNicholas TehPas encore d'évaluation
- 2016 Specimen Paper 2 Mark SchemeDocument6 pages2016 Specimen Paper 2 Mark SchemeMaheerPas encore d'évaluation
- Areas of Similar Figures: Practice QuestionsDocument2 pagesAreas of Similar Figures: Practice QuestionsNicholas TehPas encore d'évaluation
- Chem Energetics MCQDocument18 pagesChem Energetics MCQNicholas TehPas encore d'évaluation
- 9709 w12 Ms 33Document7 pages9709 w12 Ms 33Nicholas TehPas encore d'évaluation
- 9647 H2 Chemistry (2014)Document11 pages9647 H2 Chemistry (2014)Nicholas TehPas encore d'évaluation
- Ec MacrobudgetfpDocument3 pagesEc MacrobudgetfpNicholas TehPas encore d'évaluation
- Raffles Junior College Jc1 Promotion Examination 2008Document10 pagesRaffles Junior College Jc1 Promotion Examination 2008Mathathlete100% (1)
- Other School 1 EM P2Document24 pagesOther School 1 EM P2Nicholas TehPas encore d'évaluation
- Preliminary Examination: Exam Date: Duration: 2 HoursDocument22 pagesPreliminary Examination: Exam Date: Duration: 2 HoursNicholas TehPas encore d'évaluation
- Other School 2 EM P2Document19 pagesOther School 2 EM P2Nicholas TehPas encore d'évaluation
- Ec MacroiaiDocument15 pagesEc MacroiaiNicholas TehPas encore d'évaluation
- Statistics Revision SolutionsDocument10 pagesStatistics Revision SolutionsNicholas TehPas encore d'évaluation
- Ebook C Programming Program Design Including Data Structures 8Th Edition Malik Test Bank Full Chapter PDFDocument35 pagesEbook C Programming Program Design Including Data Structures 8Th Edition Malik Test Bank Full Chapter PDFrowenathuyzdwqr100% (12)
- Introduction To Systems Approach in Water Quality Decision ProblemsDocument3 pagesIntroduction To Systems Approach in Water Quality Decision ProblemsMALL SUBPas encore d'évaluation
- Section 1.1.2 Thermal Conductivity of A GasDocument2 pagesSection 1.1.2 Thermal Conductivity of A GasGho VinsenPas encore d'évaluation
- ADDDocument162 pagesADDrahimPas encore d'évaluation
- Module 3: Sampling and Reconstruction Problem Set 3Document20 pagesModule 3: Sampling and Reconstruction Problem Set 3aniPas encore d'évaluation
- (ASTM International) Manual On Presentation of DataDocument116 pages(ASTM International) Manual On Presentation of DataJuan Ros100% (1)
- 05 Modeling Dynamic and Static Behavior of Chemical ProcessesDocument47 pages05 Modeling Dynamic and Static Behavior of Chemical ProcessesAsrul SaniPas encore d'évaluation
- Frequency Response For Control System Analysis - GATE Study Material in PDFDocument8 pagesFrequency Response For Control System Analysis - GATE Study Material in PDFnidhi tripathiPas encore d'évaluation
- Syllabus For AutoCAD-3D Modeling.Document3 pagesSyllabus For AutoCAD-3D Modeling.yesuppu56Pas encore d'évaluation
- Optimized Fractional-N PLL For FMCW Radar Indoor Positioning ApplicationsDocument4 pagesOptimized Fractional-N PLL For FMCW Radar Indoor Positioning ApplicationsDragan StanicPas encore d'évaluation
- Lesson 1.3: General Properties of Indefinite IntegralsDocument6 pagesLesson 1.3: General Properties of Indefinite IntegralsMarkPas encore d'évaluation
- 15 Famous Greek Mathematicians and Their ContributionsDocument16 pages15 Famous Greek Mathematicians and Their ContributionsMallari MarjoriePas encore d'évaluation
- R7211003 Electromagnetic Waves and Transmission LinesDocument1 pageR7211003 Electromagnetic Waves and Transmission LinessivabharathamurthyPas encore d'évaluation
- Cambridge IGCSE: PHYSICS 0625/63Document16 pagesCambridge IGCSE: PHYSICS 0625/63...Pas encore d'évaluation
- COMSATS University Islamabad: Sahiwal CampusDocument8 pagesCOMSATS University Islamabad: Sahiwal CampusHamid SaeedPas encore d'évaluation
- Irstlm ManualDocument8 pagesIrstlm ManualagataddPas encore d'évaluation
- Ven DiagramDocument5 pagesVen DiagramNadine MillaminaPas encore d'évaluation
- Finite Element AnalysisDocument160 pagesFinite Element AnalysisRichie Richard0% (1)
- Marine Engineering Mtech AssignmentDocument3 pagesMarine Engineering Mtech AssignmentDaniel Inemugha100% (1)
- Research Article: CFD Study of Industrial FCC Risers: The Effect of Outlet Configurations On Hydrodynamics and ReactionsDocument17 pagesResearch Article: CFD Study of Industrial FCC Risers: The Effect of Outlet Configurations On Hydrodynamics and ReactionsAzharuddin_kfupmPas encore d'évaluation
- Unil Ecch 26 MagnetismDocument72 pagesUnil Ecch 26 Magnetismeviegonzalez211Pas encore d'évaluation
- Transitivity of PreferenceDocument5 pagesTransitivity of PreferenceAli Asgor RatonPas encore d'évaluation
- Syllogism Made EasyDocument20 pagesSyllogism Made EasympvetriveluPas encore d'évaluation
- Investment Decision Making and RiskDocument10 pagesInvestment Decision Making and RiskEdzwan RedzaPas encore d'évaluation