ENT142 ENGINEERING DYNAMICS

ZOL BAHRI RAZALI

1 |







HOW to understand Engineering DYNAMICS
Friendly notes to understand as simple as 123


Zol Bahri Razali














ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

2 |


ABSTRACT

Is an Engineering Mechanics : DYNAMICS is a tough subject?
Obviously most of engineering students at college and university
expect that the subject is tough and very difficult to understand. Why?
Maybe they have experienced with a pre-requisite subject : STATICS.
The DYNAMICS is a practical subject and an expansion of theoretical
knowledge of Statics. If really students understand and can imagine
the Free Body Diagram (FBD) in Statics, they are easy to imagine the
movement of the particle in FBD in DYNAMICS. Therefore they will
understand the concept of movement in this subject, and understand
what is DYNAMICS.

This book will guide students to understand the concept of
DYNAMICS through a method of 123, as simple as to understand
123. For engineering students at college and university, this simple
book is expected to give them to understand basic theoretical
knowledge on DYNAMICS especially in Free Body Diagram (FBD).
For individual who work at higher level of engineering such as
Engineers, Designers or Technicians, this book might be not suitable
for references because the contents is not in depth and breadth, i.e
too simple and very basic theoretical knowledge.



ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

3 |




ACKNOWLEDGEMENT

Main references of this note are from the references:

1. Hibbeler, R.C. 2002. Engineering Mechanics : Dynamics. 2
ed
.
Prentice Halls, Pearson Education Asia Pte. Ltd., Singapore.
2. Hibbeler, R.C. 2001. Engineering Mechanics : Statics. 2
ed
.
Prentice Halls, Pearson Education Asia Pte. Ltd., Singapore.
3. Hibbeler, R.C. 2010. Engineering Mechanics : Dynamics. Twelfth
Edition in SI Unit. Prentice Halls, Pearson Education South Asia
Pte. Ltd., Singapore..
4. Meriam, J.L. and Kraige, L.G. 2001. Engineering Mechanics:
Dynamics, John Willey & Sons, Inc.
5. Beer, F.P., Johnston, E.R. and Clausen, W.E. 2004. Vector
Mechanics for Engineers: Dynamics, Mc Graw Hill.






ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

4 |

CHAPTER 12

INTRODUCTION TO DYNAMICS


Chapter Objectives
To introduce the concepts of position, displacement, velocity and acceleration
To study particle motion along a straight line and represent this motion graphically
To investigate particle motion along a curved path using different coordinate
systems
To present an analysis of dependent motion of two particles
To examine the principles of relative motion of two particles using translating axes



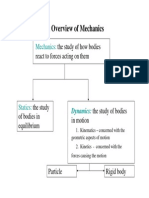
12.1 Introductions

- Mechanics branch of the physical science that is concerned with the state of
rest or motion of bodies subjected to the action of the forces

- Mechanics of rigid body - divided into statics and dynamics

- Statics - concerned with the equilibrium of the body that is either at the rest or
moves with constant velocity

- Dynamics - concerned with the accelerated motion of a body. Presented in 2 parts:
a) Kinematics geometric aspect of motion
b) Kinetics analysis of the force causing the motion
diff diff
BASICALLY: s v a

intg intg
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

5 |


12.2 Rectilinear Kinematics: Continuous Motion

Rectilinear Kinematics at any given instant, the particles position, velocity and
acceleration.

Position the straight line path of a particle. From the origin (o), position vector r specify
the location of the particle (p).












Convenient (r) represent by (s)

Displacement the change in its position
Eg : If the particle moves from P to P, the displacement is r = r- r
s = s s
















s is positive particles final position is to the right of its initial position, ie :
s>s.
Displacement of a particle vector quantity
Distance traveled is a positive vector.
r
O
s
r


r Ar


s As



s

Displacement

P P
O
s
s

Position

P
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

6 |

{Velocity}

If the particle moves through a displacement r, from P-P during the time
interval t, the average velocity

Vavg = r , V = dr : instantaneous velocity
t dt


V as an algebraic scalar, V = ds
dt










t or dt always positive:
1. particle moving the right, velocity is positive
2. particle moving to the left velocity is negative.

The magnitude of the velocity is known as the speed.
( units : m/s )
v
avg
= s
t


t

v

P P
O s

As
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

7 |

{ Acceleration }

Provided the velocity of the particle is known at two point P P, the average
acceleration

a
avg
=
t
v
A
A











v A difference in the velocity during the time interval v A = v - v

Acceleration: a =
dt
dv

a
acceleration

a =
2
2
dt
s d

a
deceleration



deceleration when the particle is slowing down
- speed decreasing
- v v v = A
1
is negative

acceleration is zero when velocity is constant.
- o v v v = = A

( unit = m/s
2
)

a ds = v dv a =
dt
dv
& v =
dt
ds






a

P P
O s

v v
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

8 |

constant acceleration each of three kinematics equations a
c
=
dt
dv

a = a
c

v =
dt
ds
, a
c
ds = vdv
maybe integrated to obtained formula
that related a,v,s,t.




The three formulas of constant acceleration :

1) Velocity as a function of time
}
=
v
vo
dv
}
t
o
c
a dt

v = v
o
+ a
c
t


2) Position as a function of time


} }
=
s
o
t
o
c
v ds ( + a
c
t) dt t a v dt ds v
c o
+ = =

s = s
o
+ v
o
t +
2
1
a
c
t
2


3) Velocity as a function of position

v.dv = a
c
.ds
} }
=
o
v
s
s
c
o o
ds a vdv

=> v
2
= v
2
0
+ 2a
c
( s-s
o
)


This formula only useful when the acceleration is constant and when t = o ,
s = s
o
, v = v
o


e.g. a body fall freely toward the earth.





+
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

9 |

See Example:

- 12.1
- 12.2
- 12.3
- 12.4
- 12.5


Exercise : 12.1
- 12.2
- 12.3
- 12.4
- 12.5




0194579207





















ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

10 |


12.3 Rectilinear Kinematics: Erratic Motion

When particles motion during a time is erratic, may best be describes graphically using a
series of curves.

Using the kinematics equations:


dt
dv
a = = v
dt
ds
dv v ds a . . =

a) Given s-t graph, construct the v-t equations


s










t



b) t v graph t a graph













v = , dt ds
By experimentally, if the position can
be determined during the time of
period, graph s-t can be plotted.

By v = , dt ds the graph v-t can be
plotted.
( slope of s-t graph = velocity ).
dt
dv
a =


dt
dv
a =
(slope of t v graph = acceleration)

See example 12.6, page 19
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

11 |

c) t a graph , t v graph













































using dt ds a = ,
A
}
= adt v

( change in velocity = area
under t a ) graph. )

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

12 |

d) t v graph t s graph













































dt ds v = A
}
= vdt s

(displacement = area under t v
graph)

See example 12.7, page 21

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

13 |

e) s a graph s v graph.

dv v ds a . . =

between the limits
o
v v = at
o
s s =

2
1
( )
2
0
2
1
v v =
}
1
.
s
s
o
ds a

1
v v = at
1
s s = = area under s a graph

















f) s v graph s a graph

dv v ds a . . =

) (
ds
dv
v a =

acceleration = velocity x slope of s v graph.


See Example 12.8.
Exercise:
- 12.42
- 12.43
- 12.44
- 12.45
- 12.46
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

14 |


12.4 General Curvilinear Motion

- curvilinear motion occurs when the particle moves along a curved path.


- position- considered a particle located
at point p on a space curve defined by
the path function s.

- position vector r = r ( t )
- magnitude and direction change as the
particle moves along the curve.






- displacement- during small line At, the
particle moves a distance As along the
curves.

r = r + Ar

- the displacement Ar represent the
change in the particles position.


Ar = r - r





- velocity during the time t A , the average
velocity.

V
avg
=
t
r
A
A
, V =
dt
dr


- dr will be tangent to the curve at p, the
direction of V is also tangent to the
curve.


Path
P


r s
O

s

Position
P
As

Ar P
r
r
O


s

Displacement
v



P

r


O

s

Velocity
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

15 |


The magnitude of v, called speed. V =
dt
ds
.

V
t
v
avg
A
A
=
, where Av = v
1
- v

Instant a new acceleration, t A 0


dt
dv
a =


2
2
dt
r d
a =

Velocity vector is always directed
tangent to the path.


a tangent to the hodograph, not tangent
to the path of motion.

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

16 |


12.5 Curvilinear Motion: Rectangular Components

Displacement

r = xi + y j + zk

magnitude of r always positive

r = (x
2
+ y
2
+ z
2
)

unit vector u
r
= (1/r)r



Velocity

v = v
x
+ i v
y
+ j vZ k

v =
dt
dr
=

dt
d
( xi ) +
dt
d
( y j ) +
dt
d
( z k )

v =
dt
dr
= v
x
i + v
y
j + v
z
k ,
where : v
x
=
.
x
v
y
=
.
y

v
z
=
.
z


The velocity has a magnitude defined as the positive value of

v = (v
x
2
+ v
y

2
+ v
z
2
)






ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

17 |

Acceleration :



a =
dt
dv
= a
x
i + a
y
j
+ a
z
k

where : a
x
=
.
x
v =
..
x
a
y
=
.
y
v =
..
y
a
z
=
.
z
v =
..
z




The acceleration has a magnitude defined by the positive value of

a = (a
x
2
+ a
y
2
+ a
z
2
)



See Example 12.9 and 12.10.
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

18 |


12.6 Motion of a Projectile

The free-flight motion of a projectile studied in terms of its rectangular
components. The projectiles acceleration always acts in the vertical direction.

Projectile launched at point (
o
x ,
o
y ) , initial velocity is V
o
, having two components
( V
o
)
x
and ( V
o
)
y
. The projectile has a constant downward acceleration,
a
c
= g = 9.81
2
s m .




















Horizontal motion : -

Since a
x
= 0 ; v = v
o
+ a
c
t ; v
x
= ( v
o
)
x

x = x
o
+ v
o
t +
2
1

at
2

; x = x
o
+ ( v
o
)
x
t

v
2
= v
o
2
+ 2a
c
( s-s
o
) ; v
x
= ( v
o
)
x



First and last equation indicated that the horizontal component of velocity always remains
constant during the motion.









ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

19 |

Vertical motion : -

Since a
y
= -g. + v = v
o
+ a
c
t ; v
y
= ( v
o
)y gt.

y = y
o
+ v
o
t +
2
1
a
c
t
2
; y = y
o
+ (v
o
) yt -
2
1
g

v
2
= v
o
+ 2 a
c
( y- y
2
) ; v
y
2
= (v
o
)
2
-2g (y)

Only two of the above three equations are independent of one another.

Problems involving the motion of projectile can have at most three unknowns
since only three independent equations can be written.

- one equations in the horizontal direction.
- two equations in the vertical direction.

Once v
x
and v
y
are obtained, the resultant velocity v which is always tangent to the
path.


See Example:
- 12.11
- 12.12
- 12.13
Exercise:
- 12.71
- 12.72
- 12.73
- 12.74
- 12.75

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

20 |


12.7 Curvilinear motion: Normal and tangential components

When the path along which a particle is moving is known, it is convenient to
describe the motion using n and t components (normal and tangent) to the path, and at the
instant considered here their origin located at the particle.


Planer motion :-


( at instant considered )
o - center of curvature.
s - radius of curvature.

taxis - tangent to the curve at P.

n-axis - perpendicular to the t- axis,
directed from P towards the center of
curvature.

Positive direction , will be designated
by the unit vector, u
n
( normal ) and u
t

( tangent ).







Velocity :-

Since the particle moving , s is a function of time. The particle velocity v has a
direction that is always tangent to the path, and the magnitude that is determined by
taking the time derivative of the path function s = s(t) .

v =
dt
ds


v = vu
t


where v =
.
s



ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

21 |

Acceleration :-

The acceleration of the particle is the time rate of the change of the velocity.
a =
.
v =
.
v u
t
+ v
.
u
t



by formulation ,


.
u
t
=
.
o u
n
=
s
s
.
u
n
=
s
v
u
n



substitute to the above equation

a = a
t
u
t
+ a
n
u
n


where a
t
=
.
v

or a
t
ds = v.dv

and a
n
=
s
v
2



magnitude of acceleration is the
positive value of a =
2 2
n t
a a +



Two special cases of motion :

1) The particle moves along a straight line , s .
o a
n
= ,
t
a a = =
.
v
The tangential components of acceleration represents the time rate of change in the
magnitude of the velocity.

2) The particle moves along a curve with a constant speed then
. ,
2
.
s v a a o v a
n t
= = = =

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

22 |


12.8 Relative motion analysis of two particles using Translating Axes


Position :


The axes of this frame are only persuitted to
translate relative to the fixed frame . The
relative position of B with respect to A
is designate by a relative position vector
r
A B
.


r
B
= r
A
+ r
A B





Velocity : An equation that related the velocities of the particle can be determined by
taking the time derivative.

v
B
= v
A
+ v
A B


where v
B
=
dt
dr
B


v
A
=
dt
dr
A


v
A B
=
dt
dr
A B



v
B
and v
A
- refer to absolute velocities
- observed from the fixed frame.

v
A B
- relative velocity
- observed from the translating frame.





v
B/A

v
B


v
A

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

23 |

Acceleration :


A B A B
a a a + =



A B
a is the acceleration of B as seen by the observer located at A and translating with
the x,y,z reference frame.





































a
B/A



a
A
a
B

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

24 |

CHAPTER 13

KINEMATICS OF A PARTICLE
(FORCE & ACCELERATION)


Chapter Objectives
To state Newtons Law of Motion and Gravitational Attraction and to define mass
and weight
To analyze the accelerate motion of a particle using the equation of motion with
different coordinate systems.
To investigate central force motion and apply it to problems in space mechanics




13.1 Newtons Law of Motion

Galileo (1590) - experiment to study the motion of pendulum and falling bodies.
- the effects of forces acting on bodies in motion.

Isaac Newton (1687)

o 1
st
Law - A particle originally at rest, or moving in the straight line
with a constant velocity, will remain in this state provided
the particle is not subjected to an unbalanced force.

o 2
nd
Law A particle acted upon by an unbalanced force F,
experiences an acceleration a that has the same direction as the
force and a magnitude that is directly proportional to the force.

o 3
rd
Law The mutual forces of action and reaction between two
particles are equal, opposite and collinear.

Note : - The unbalanced force acting on the particle is proportional to the time rate of
the change of the particles linear momentum.

Newtons 2
nd
law of motion relates the accelerated motion of a particle to the force
that act on it.

F = ma where m: mass of the particle.
( equation of motion )

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

25 |

Since m is constant , we can also write F =
dt
mv d ) (
, where mv is the particles
linear momentum.

Albert Einstein ( 1905 ) developed the theory of relativity and place limitation on
on the use of Newtons second law.


~ Newtons Law of Gravitational Attraction ~

F = G
r
m m
2 1
where :
F force of attraction between two particles

G - universal constant of gravitation
G = 66.73 + 10
12
2
3
kgs
m


m
1
,m
2
- mass of each of the two particles

r - distance between centre.


~ Mass and weight ~

Property of matter by which we can compare the response of one body with that of
another.

w = m.g , w weight

by comparison F = ma , we term g the acceleration due to gravity.














m (kg)


a = g (m/s
2
)


W = m.g (N)

SI system
[W = m.g (N)]

[g = 9.81
2
s
m
]
Weight w = kg
2
s
m


= N
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

26 |


13.2 The equation of motion

The resultant force F
R
= EF
EF = a m.















The resultant of these forces produce the vector a m. , its magnitude and direction can be
represented on the kinetic diagram.


F
2
F
2

F
R
= EF
P ma
F
1
P
F
1

a
F.B.D. Kinetic diagram
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

27 |


13.3 Equation of motion for a system of particles

F
i
+ F
i
=
i i
a m ( EF = ma )

where F
i
- resultant ext. force.
f
i
- resultant int. force.


a
ma = E
i i
a m EF = . . . g a m


If r
a
is position vector which locates at the center of mass G.

Spring If the particle is connected to an elastic spring.

F
s
= ks

s =
o
l l

where : = l deformed length

o
l = unreformed length.


Kinematics If the velocity are position of the particle is to be found, apply the
kinematics equation.

acceleration is a function of time.


dt
dv
a = ,
dt
ds
v =

acceleration is a function of displacement : integrate . . . dv v ds a =

acceleration is constant , to determined the velocity or position of the particle.

- v = v
o
+ a
c
t

- s = s
o
+ v
o
t +
2
1
a
c
t
2


- v
2
= v
o
2
+ 2
c
a ( s-s
o
)

In all cases, make sure the positive inertial coordinates directions.


m
i
a
i

Kinetic diagram
F
i


f
i


F.B.D.
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

28 |


13.4 Equation of motion : rectangular coordinates

When the particle moving relative to a inertial x, y, z frame, the force acting
maybe expressed in term of their i, j, k. components.

EF = a m.
EF i
x
+ EF
y
j + EF
z
k = ) ( k a j a i a m
z y x
+ +

EF
x
=
x
a m.
EF
y
=
y
a m . .
EF
z
=
z
a m.


Procedure for analysis.

1) FBD :- Draw the FBD, it provides a graphical representation that accounts for all
the forces (EF) which act on the particle.

2) Equation of motion :- use scalar or Cartesian vector analysis (3-D)for the solution.

a) Friction :

If the particle contacts the rough surface, it maybe necessary to use the frictional
Equation.


F
f
= . N
k
where :

[ F
f
always act on the FBD such
k
- coefficient of kinetic friction.
that it opposes the motion of the F
f
- magnitude of the friction
particle relative to the surface it N - Normal forces.
contacts ]


See Example:
- 13.1
- 13.2
- 13.3
- 13.4

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

29 |

Exercise : 13.1
- 13.2
- 13.3
- 13.4
- 13.5

13.5 Equation of motion : Normal and tangential coordinates

When the particle moves over a curved path, the equation of motion for the
particle maybe written in the tangential, normal and binormal directions.

EF = ma

EF
t
u
t
+ EF
n
u
n
+ EF
b
u
b
=
n t
a m a m . . +

where F
t
,F
n
, F
b
- force components acting on the particle in the tangential, normal and
binormal.


There is no motion of the particle in the binormal direction, since the particle is
constrained to move along the path.

EF
t t
a m. =
dt
dv
a
t
= ( time rate of change in the
magnitude of velocity )
EF
n n
a m. =

EF . o
b
=

EF
t
acts in the direction of motion, the particles speed will be increase.
Opposite direction, the speed will slow down.

g
v
a
n
2
= ( time rate of change in the velocity direction )

vector always acts in the positive n direction ( toward the paths centre of
curvature), EF
n
which cause
n
a , also acts in this direction.




ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

30 |













Procedure for Analysis

The motion of a particle along a known curved path, normal and tangential coordinates
should be considered.

FBD Draw the FBD for the particle

Equation of motion as mention

Kinematics
g
v
an
ds
dv
v at
dt
dv
a
t
2
, . , = = =

If the path is defined as y = f (x), the radius of curvature at the
point where the particle located can be obtained:

= [1 + (
dx
dy
)
2
]
3/2
/ ,d
2
y / dx
2
,

See Example:
- 13.6
- 13.7
- 13.8
- 13.9

Exercise : 13.48
- 13.49
- 13.50
- 13.51
- 13.52
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

31 |

CHAPTER 14

KINEMATICS OF A PARTICLE
(WORK AND ENERGY)


Chapter Objectives
To develop the principle of work and energy and apply it solve problems that
involve force, velocity and displacement
To study problems that involves power and efficiency
To introduce the concept of a conservative force and apply the theorem of
conservation of energy to solve kinetics problems



14.1 The work of a force

A force F does work when the particle undergoes a displacement in the direction
of the force.

Eg : particles moves along the paths, from
position r to r, dr = r r, where dr = ds. If
the angle u, the work dU is done by F is a
scalar quantity

dU = F.ds cos u

Definition of the dot product dU = F.dr

dU = F.ds cos u
= F.dr

dU = 0 when F perpendiculars.
dr = ds cos u

Work of a variable force.


If the particle undergoes finite displacement
along its path, s
1
to s
2
, work is determined
by integration.


u
2 1
=
}
=
2
1
.
s
r
dr F
}
2
1
cos
s
s
F u.
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

32 |




If ( F cos u vs s ) is plotted, working
components as the area under the curve,
from position s
1
to s
2
.






Work of constant force moving along a straight line









If the F
c
has a constant magnitude and acts at a constant angle u from its straight line
path, so work done F
c
is

u
2 1
= F
c
cos u
}
2
1
s
s
d s
= F
c
cos u ( s
2
- s
1
).

Work F
c
represents the area of the rectangle.

Work of weight

The particle moves along the path s, from s
1
to s
2
.At the immediate point, the
displacement dr = dxi + dy j + dz k .
Since w = -w j

u
2 1
=
}
dr f .

=
}
+ +
2
1
) ).( (
r
r
dzk dyj dxi wj

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

33 |

=
}
=
2
1
1
1
1 2
) ( y y w wdy
u
2 1
= -w (y
2
- y
1
)

This, work done is equal to the magnitude of
the particles weight times its vertical displacement.



Work of spring

The magnitude of force developed in a linear elastic spring when the spring is displaced a
distance s from its unstreched position is F
s
= k
s
, where k is the spring stiffness. If the
spring is elongated or compressed from a position s
1
to a further position s
2
, the work
done on the spring by F
s
is positive, since in each case, the force and displacement are in
the same direction.

U
1-2
=
}
2
1
s
s
Fsds =
}
2
1
s
s
ksds

= .
2
1
2
1
2
1
2
2
ks ks
















When the particle is attach to a spring, then the force Fs exerted on the particle is
opposite to that exerted on the spring.

The force will do negative work on the particle when the particle is moving so as a
further elongate ( or compress ) the spring.

U
1-2
= - ( ).
2
1
2
1
2
1
2
2
ks ks

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

34 |

If both same direction positive work .opposite direction negative work.
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

35 |


14.2 Principle work and energy

If the particle has a mass, m and is subjected to a system of external forces, represented
by the resultant F
R
= EF
t
= ma
t
.

Applying the kinematics equation:




ds
dv
v a
t
. =

}
2
1
s
s
t
ds F =
}
2
1
.
v
v
mvdv
=
2
1
2
2
2
1
2
1
mv mv







EU
2 1
= the sum of the work done by all the forces acting as the particle
moves from point 1 -2.

T =
2
2
1
mv T = particle final kinetic energy
mv
2
1
2
= particle initial kinetic energy
T
1
+ EU
1-2
= T
2


Note : i ) EF
t
=
t
a m. , to obtain
t
a , integrate
t
a = . .
ds
dv
v

ii ) EF
n
=
n
a m. cannot be used, since these force do no work on the particle on
the forces directed normal to the path.










ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

36 |

Procedure for analysis

The principle of work and energy is used to solve the kinetic problems that involve
velocity , force and displacement.


FBD : Draw FBD in order to account for all the forces.

Principle of w = E :

T
1
+ EU
1-2
= T
2


Kinetic energy at the initial / final point always positive T =
2
2
1
mv

A forces does work when it moves through its displacement in the direction of the
force.( +ve same direction )

Force that are functions of displacement must be integrate to obtain the work.

The work of a weight weight magnitude and the vertical displacement.
U
w
= w
y
( + + ).

The work of spring ,
s
=
2
1
ks
2
.

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

37 |


14.3 Principle of Work and Energy for a system of particles




th
i particles
m
i
mass
F
i
resultant external force
f
i
resultant internal force





Which applies in the tangential direction, the principle of work and energy:


} }
= + +
2
1
2
1
2
2
2
2
1
) ( ) (
2
1
i
i
i
i
s
s
s
s
i i t t i i
v m ds fi ds Fi v m


For all of the
th
i particles.



}

}

= + +
2
1
2
1
2
2
2
1
2
1
) ( ) (
2
1
i
i
i
i
s
s
i
s
i i t t i i
v m ds fi ds Fi v m


ET
1
+ EU
2 1
= ET
2


systems final
kinetic energy

work done by all the
external or internal forces.


systems initial kinetic energy.









ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

38 |

Work of Friction Caused by Sliding.




The cases where a body is sliding over the
surface on another body in the presence of
friction.






Applied force P just balance the resultant
friction force . .N
k





2 2
2
1
2
1
mv N Ps mv
s k
= +

is satisfied when P =
k
N



The sliding motion will generate heat, a form of energy which seems not to be accounted
for in the W&E equation.

See Example:
- 14.2
- 14.3
- 14.4
- 14.5
- 14.6
Quiz:
- 14.1 14.41 (each student has to answer one question)
v v

P P



s
W


P



F =
k
N

N
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

39 |


14.4 Power and Efficiency

Defined as the amount of work performance per unit of time.

P =
dt
du
where du = F.dr
=
dt
dr F.

= F.
dt
dr
or P = F.V.

Power is a scalar, where in the formulation; V represents the velocity of the point which
is acted upon by the force, F.

I Wa H = I
s
J
= I N.
s
m
= I w

Note:

The term power provides the useful basis for determining the type of motor or
machine which is required to do a certain amount of work in a given time. For example,
two pumps may each be able to empty a reservoir if given enough time, however the
pump having the larger power will be complete the job sooner.



The mechanical efficiency of a machine is defined as the ratio
of the output of useful power produce by the machine to the
input of power supplied to the machine.


input power
output power
E

=

If the energy applied,
input energy
output energy
E

=

Since machines consist of a series of moving parts, frictional forces will always be
developed within the machine, and as result, extra energy or power is needed to
overcome these forces.

The efficiency of a machine is always less than 1




Power
Efficiency

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

40 |

Procedure for Analysis

o Determine the external force F
o If accelerating , a m F . = E
o One F and V have been found, P = F.V = Fr cosu
o In some problem F per unit time, P =
dt
du



See Example:
- 14.7
- 14.8
Exercise
- 14.42
- 14.43
- 14.44
- 14.45
- 14.46
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

41 |


14.5 Conservative forces and potential energy

Conservative force

When the work done by a force in moving a particle from one point to another is
independent of the path followed by the particle, the force is called a conservative
force.

e.g. : - weight of the particle
: - the force of an elastic spring

weight depends on the particles vertical displacement
spring depends only on the extension/compression.

in contrast force of friction exerted on a moving objects depends on the
path/neoconservative.

Potential Energy

Energy - capacity for doing works.
- from the motion of particle kinetic energy.
- from the position of particle ( fixed datum / reference ) - potential
energy
(potential energy due to gravity ( weight ) and elastic spring is important.)

Gravitational potential energy: V
g
= Wy



















ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

42 |

Elastic potential energy: V
e
=
2
2
1
s
k


[ V
e
always + ve, the spring has the
capacity for always doing positive
work ] when the spring back to
outstretch position.










Potential Function

If a particle is subjected to both gravitational and elastic forces, - potential function.

V = V
g
+ V
e


U
2 1
= V
1
- V
2
work done by a conservative force.


E.g. : potential function for a particle of
weight W, suspended from a spring can be
expressed in term of its position, s ,
measured from a datum.

V = V
g
+ V
e

= - W(s) +
2
2
1
ks



If the particle moves from s
1
to lower s
2
,


U )
2
1
( )
2
1
(
2
2 2
2
1 1 2 1 2 1
ks Ws ks Ws V V + + = =

= )
2
1
2
1
( ) (
2
1
2
2 1 2
ks ks s s W

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

43 |


14.6 Conservation of Energy

When the particle acted upon by a system of both conservative and neoconservative,
work done by conservative position.

+ = + +
2 2 2 1 1 1
) ( V T noncons U V T

If noncons is zero =>
2 2 1 1
V T V T + = +

Note : conservative force (not follow the path ) weight / spring
neoconservative force (follow exactly the path ) friction.

2 2 1 1
V T V T + = + conservation of mechanical energy, conservation energy.


Note : during the motion, sum of potential and kinetic energies remains constant.
For this occur, kinetic energy must be transformed into potential energy and
vice versa.


E.g. : The ball of weight w is dropped from a height, h above the ground (datum).

at initial position, mechanical energy
E = T
1
+ V
1

= ) (
2
1
2
1 g e
v v mv + +
= wh mv +
2
1
2
1

= 0 + wh
= . wh


When the ball has fallen a distance ,
2
h
its speed can be determined by using:

) ( 2
2
0
2
o c
y y a v v + = Therefore:
= ) ( 2
o c
y y a
= )
2
( 2
h
g
2 2
T V E + =
v = )
2
( 2
h
g =
2
) (
2
1
)
2
( gh m
h
w +
= gh 2 =
2
) (
2
1
)
2
( gh
g
w
h
w +
= . wh
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

44 |


When the ball strikes the ground, P.E. (0) and

) ( 2
2 2
o c o
y y a v v + = Total energy:
= ) .( . 2 h g
= gh 2
3 3
T V E + =
=
2
) 2 (
2
1
0 gh
g
w
+
= . wh




































ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

45 |

CHAPTER 15

KINETICS OF A PARTICLE:
IMPULSE & MOMENTUM



Chapter Objectives
To develop the principle of linear impulse and momentum for a particle
To study the conservation of linear momentum for particles
To analyze the mechanics of impact
To introduce the concept of angular impulse and momentum
To solved problems involving steady fluid streams and propulsion with variable
mass



15.1 Principle of Linear Impulse & Momentum

- Equation of motion for a particle of mass m:

= =
dt
dv
m ma F

- Rearranging:

} }
=
2
1
1
2
t
t
v
v
dv m dt F

or

}
=
2
1
1 2
t
t
mv mv dt F











Eq. 1
Linear Momentum
principle of linear impulse &
momentum
(time integration of the
equation of motion)
linear particles
impulse linear
momentum
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

46 |

- Vector of L = mv in Eq. 1 is referred to as the particles linear momentum
- Magnitude of mv units of mass-velocity




- Integral I = } F dt in Eq. 1 is referred to as the linear impulse
- Measures the effect of a force during the time the force acts.
- Magnitude: force-time
- If force expressed as a function of time, impulse = direct evaluation of the integral
- If force constant direction during the time period t
1
to t
2
, impulse = area under the
curve of force vs. time:
}
=
2
1
t
t
dt F I

- If force constant in magnitude & direction:
= =
}
) (
1 2
2
1
t t F dt F I
c
t
t
c
shaded rectangular area
















2 1
2
1
mv dt F mv
t
t
= +
}

- Initial momentum of the particle at t
1
plus the vector sum
of all the impulses applied to the particle during the time
interval t
1
to t
2
is equivalent to the final momentum of the
particle at t
2
.

Linear Impulse
Principle of Linear Impulse & Momentum
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

47 |








- The scalar x, y, z components of the previous equation are:
2 1
2 1
2 1
) ( ) (
) ( ) (
) ( ) (
2
1
2
1
2
1
z
t
t
z z
y
t
t
y y
x
t
t
x x
v m dt F v m
v m dt F v m
v m dt F v m
= +
= +
= +
}

- To solve a linear impulse and momentum:

a) FBD - establish the x, y, z inertial frame of reference
- draw the particles FBD account for all the forces that produce impulses on
the particle
- establish direction & sense of the particles initial & final velocities

b) Principle of Impulse & Momentum
- apply the principle:
2 1
2
1
mv dt F mv
t
t
= +
}

- if motion occurs on x-y plane the 2 scalar component equation can be formulated
by:

1. resolving the vector components of F from FBD
2. using the data on the impulse and momentum diagrams









Scalar Equation
Procedure for Analysis
See Example:
- 15.1
- 15.2
- 15.3
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

48 |






15.2 Principle of Linear Impulse & Momentum for a System of Particles


=
dt
dv
m F
i
i i







- Multiplying both sides by dt and integrating between the limits t = t
1
, v
i
= (v
i
)
1
&
t = t
2
, v
i
= (v
i
)
2
,


}

= +
2 1
) ( ) (
2
i i
t
t
i i i
v m dt F v m



The initial linear momenta of the system
added vectorially to the impulses of all
the external forces acting on the system
during the time period t1 to t2 are equal
to the systems final linear momenta.



- Location of mass centre G of the system:

= =
i i i G
m m r m r m ,

- Taking the time derivatives:

=
i i G
v m v m




Total linear momentum of the system of particles plus (vectorially)
the external impulses acting on the system of particles during the
time interval t
1
to t
2
equal to the aggregate particles final linear
momentum.
Sum of
external
forces
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

49 |





15.3 Conservation of Linear Momentum for a System of Particles

- When the sum of the external impulses acting on a system of particles is zero:


=
2 1
) ( ) (
i i i i
v m v m


- In other form:
2 1
) ( ) (
G G
v v =

- Applied when particles collide or interact.

- Nonimpulsive forces: - causing negligible impulses
- including any force that is very small compared to other
larger (impulsive) forces

- Impulsive forces: - forces which are very large & act for a very short period
of time; produce a significant change in momentum
- normally occur due to an explosion or the striking of one
body against another





















conservation of linear momentum
See Example:
- 15.4
- 15.5
- 15.6
- 15.7
- 15.8
Exercise:
- 15.32
- 15.33
- 15.34
- 15.35
- 15.36
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

50 |





15.4 Impact

- Impact occurs when two bodies collide with each other during a very short period
of time causing relatively large (impulsive) forces to be exerted between two
bodies.
- E.g.: striking of a hammer on a rail golf club on a ball

- Central impact the direction of motion of
the mass centers of the two colliding
particles is along a line passing through the
mass centers of the particles






- Oblique impact when the motion of one or
both of the particles is at angle with the line
of impact






- Particle have the initial momenta, (v
A
)
1
> (v
B
)
1

- During the collision the particles will undergo a period of deformation equal but
opposite deformation impulse } P dt
- At maximum deformation both particles move with common velocity v
- Then a period of restitution occurs (particles will either return to original shape or
remain deform) restitution impulse } R dt pushes particles apart from another,
where } P dt > } R dt
- Just after separation, particles final momenta = (v
B
)
2
> (v
A
)
2

Analysis of Central Impact
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

51 |



- To determine the velocities, apply conservation of momentum for the system of
particles by referring to the figure above:

+ m
A
(v
A
)
1
+ m
B
(v
B
)
1
= m
A
(v
A
)
2
+ m
B
(v
B
)
2


- To solve for final velocities (initial values of particles will be known in most
cases), consider deformation phase:

+ m
A
(v
A
)
1
- } P dt = m
A
v

- For restitution phase:

+ m
A
(v
A
)
1
- } R dt = m
A
( v
A
)
2


- Ratio of the restitution impulse to the deformation impulse = coefficient of
restitution, e:

v v
v v
dt P
dt R
e
A
A

= =
}
}
1
2
) (
) (


- For particle B:
1
2
) (
) (
B
B
v v
v v
dt P
dt R
e

= =
}
}


- If remove unknown v:
1 1
2 2
) ( ) (
) ( ) (
B A
A B
v v
v v
e

=

+
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

52 |




- In general, value of e = between zero and one:

1. Elastic Impact (e = 1): If the collision between the two particles is perfectly
elastic, deformation impulse } P dt = equal and opposite to restitution impulse
} R dt

2. Plastic Impact (e = 0): No restitution impulse given to the particles (} R dt = 0);
after collision, both particles couple or stick together and move with common
velocity.





- Use the following two equations:
1. The conservation of momentum applies to the system of particles,
Emv
1
= Emv
2

2. The coefficient of restitution, e = [(v
B
)
2
(v
A
)
2
] / [(v
A
)
1
(v
B
)
1
], relates the
relative velocities of the particles along the line of impact, just before and
just after collision.






- In determining (v
Ax
)
2
, (v
Ay
)
2
, (v
Bx
)
2
and (v
By
)
2
,
consider these four equations:
1. Momentum of the system is conserved along
the line of impact, x axis, so that Em(v
x
)
1
=
Em(v
x
)
2

2. The coefficient of restitution, e = [(v
Bx
)
2

(v
Ax
)
2
] / [(v
Ax
)
1
(v
Bx
)
1
], relates the relative
velocity components of the particles along the
line of impact (x axis)
3. Momentum of particle A is conserved along
the y axis, perpendicular to the line of impact,
since no impulse acts on particle A in this
direction.
4. Momentum of particle B is conserved along
the y axis, perpendicular to the line of impact,
since no impulse acts on particle B in this
direction.
Coefficient of Restitution
Procedure for Analysis
(Central Impact)
Procedure for Analysis
(Oblique Impact)
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

53 |

See Example:
- 15.9
- 15.10
- 15.11



15.5 Angular Momentum

- Angular momentum of a particle about point O = moment of the particles
linear momentum about O.
- Also being referred to as the moment of momentum.





- If a particle is moving along a curve lying in the
x-y plane, magnitude of Ho:

(H
o
)
z
= (d)(mv)

- Common unit = kg m
2
/ s
- Direction right-hand rule




- If the particle is moving along a space curve, angular momentum Ho:

Ho = r x mv

- In Cartesian components:
z y x
z y x
mv mv mv
r r r
k j i
Ho=








Scalar Formulation
Vector Formulation
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

54 |

CHAPTER 16

PLANAR KINEMATICS OF
A RIGID BODY



Chapter Objectives
To classify the various types of rigid-body planar motion
To investigate rigid-body translation and show how to analyze motion about a
fixed axis
To study planar motion using an absolute motion analysis
To provide relative motion analysis of velocity and acceleration using a translating
frame of reference
To show how to find the instantaneous center of zero velocity and determine the
velocity of a point on a body using this method
To provide a relative motion analysis of velocity and acceleration using a rotating
frame of reference




16.1 Rigid-Body Motion






Particles of a rigid body move along paths equidistant from a fixed plane
Has 3 types:

1. Translation
- every line segment on the body remains parallel to its original direction during the
motion
- rectilinear translation: path of motion along equidistant straight lines
- curvilinear translation: path of motion along curved lines which are equidistant









Planar motion
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

55 |

2. Rotation about a fixed axis
- all particles of the body (except those lie on the
axis of rotation) move along circular paths



3. General plane motion
- undergoes a combination of translation
and rotation

















16.2 Translation












Position:
- location of points A and B defined from fixed x, y reference frame using
position vectors r
A
and r
B

- x,y coordinate system fixed in the body where origin = A (base point)
- position of B with respect to A = relative position vector r
B/A
(r of B with respect to
A)
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

56 |

- vector addition: r
B
= r
A
+ r
B/A


Velocity:
- relationship between instantaneous velocities of A and B obtained by taking the
time derivative of the position equation:


v
B
= v
A
+ dr
B/A
/dt

Since dr
B/A
/dt = 0 due to the magnitude of r
B/A
= constant, and v
B
= v
A
= absolute
velocities,
v
B
= v
A

Acceleration:
- time derivative of velocity equation:

a
B
= a
A


- velocity and acceleration equation indicates that all points in a rigid body
subjected to either rectilinear or curvilinear translation move with the same velocity
and acceleration.



16.3 Rotation About a Fixed Axis

Angular motion

- only lines or bodies undergo angular motion
- angular motion of a radial line r located within the shaded plane and directed from
point O on the axis of rotation to point P


1. Angular position

- angular position or r = defined by angle u
- measured between a fixed reference line and r


2. Angular displacement

- defined by the change in the angular position,
measured as a differential du
- has a magnitude of du, measured in degrees, radians
or revolutions, where 1 rev = 2t rad.
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

57 |

- Since motion is about a fixed axis, direction of du
which always along the axis
- Direction determine by the right hand rule





3. Angular velocity

- defined as the time rate of change in angular position,
e, where e = du / dt +

- has a magnitude measured in rad/s
- direction always along the axis of rotation where
the sense of rotation being referred as clockwise or
counterclockwise
- arbitrarily chosen counterclockwise as positive


4. Angular acceleration

- measures the time rate of change of the angular velocity
- magnitude: o = de / dt or o = d
2
u / dt
2
+

- direction depends on whether e is increasing or decreasing
- e.g.: if e is decreasing, o = angular deceleration, direction opposite to e
- by eliminating dt from the above equation,

o du = e de +


5. Constant angular acceleration

- when angular acceleration of the body is constant,

o = o
c


+ e = e
o
+ o
c
t

+ u = u
o
+ e
o
t + o
c
t
2


+ e
2
= e
o
2
+ 2o
c
(u - u
o
)

where u
o
= initial angular position
e
o
= initial angular velocity
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

58 |









Motion of point P
- as rigid body rotates, point P travels along a circular
path of radius r and center at point O.

1. Position
- defined by the position vector r, which extends from
O to P


2. Velocity
- has a magnitude of u
u

r v r v
r
= = ,
- since r = constant, u
u

r v v r v
r
= = = = , 0
- since r v e u e = = ,

- direction of v = tangent to the circular path
- magnitude and direction of v accounted from:
p
r v = e

where r
p
: directed from any point on the axis of rotation
to point P

- to establish the direction of v right hand rule
- by referring to the figure,
since
r v
r v r r
r v
p
p
=
= =
=
e
e |
| e
, sin
sin



3. Acceleration
- can be expressed in terms of its normal and tangential components:
where
r a r a
dt d r v r
v a dt dv a
n t
n t
2
2
,
, / , ,
/ , /
e o
e o e

= =
= = =
= =

- tangential components represents the time rate of change in the velocitys
magnitude
- normal component time rate of change in the velocitys direction
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

59 |

- acceleration in terms of vector cross product:
since
) (
&
: :
p p
p
p
p
p
r r a
r v
dt
dr
dt
d
dt
dr
r
dt
d
dt
dv
a
+ =
= = =
+ = =
e e o
e
e
o
e
e


- by referring to the next figure, r r a
p t
o | o = = sin
- applying right hand rule yields
p
r o in the direction
of a
t

- hence obtain
r r
a a a
n t
2
e o =
+ =

- magnitude:
2 2
t n
a a a + =




Procedure for Analysis:

To determine velocity and acceleration of a point located on a rigid body that is rotating
about a fixed axis:

a) Angular Motion
1. Establish positive sense of direction along the axis of rotation and show it
alongside each kinematics equation as it is applied.
2. If a relationship is known between any two of the 4 variables o, e, u and t, then a
third variable can be obtained by using one of the following kinematics equation
which relates all 3 variables:
e e u o
e
o
u
e d d
dt
d
dt
d
= = = , ,
3. For constant angular acceleration, use:
) ( 2
0
2
0
2
2
2
1
0 0
0
u u o e e
o e u u
o e e
+ =
+ + =
+ =
c
c
c
t t
t

4. o,e, u - determine from algebraic signs of numerical quantities.

b) Motion of P
1. Velocity of P and components of acceleration can be determine from:
r a
r a
r v
n
t
2
e
o
e
=
=
=

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

60 |

2. If geometry of problem is different to visualize, use:
r r a
r r a
r r v
p n
p t
p
2
) ( e e e
o o
e e
= =
= =
= =

Note:
- r
p
directed from any point on the axis of rotation to point P
- r lies in the plane of motion P
- vectors expressed in terms of its i, j, k components.

See Example 16.1 and 16.2.



16.5 Relative-Motion Analysis: Velocity

General motion: combination of translation and
rotation
To view motions separately use relative-
motion analysis, involving 2 sets of coordinate
axes
Fixed reference measures the absolute position
of 2 points A & B on the body
Translating reference do not rotate with the
body; only allowed to translate with respect to
the fixed frame; origin attached to the selected
base point A







- Position vector r
A
specifies the location of base point A
- Relative position r
B/A
locates point B with respect to point A
- by vector addition, position of B: r
B
= r
A
+ r
B/A






- Points A & B undergo displacements dr
A
& dr
B
during an instant of time dt
- Consider general plane motion by its component parts:
- entire body translates by dr
A
A moves to its final position and B to B
Position
Displacement
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

61 |

- rotated about A by du - B moves to its final position (relative displacement
dr
B/A
)
- displacement of B:
A B A B
dr dr dr
/
+ =



















- to determine the relationship between the velocities of points A and B take the
time derivative (divide displacement equation by dt):
dt
dr
dt
dr
dt
dr
A B A B /
+ =






A B A B
v v v
/
+ =












absolute
velocities of
points A & B
Velocity
due to rotation about A

due to translation of A

due to translation & rotation

relative
velocity
v
B/A

relative velocity of B with
respect to A

velocity of base point A

velocity of point B
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

62 |

- since v
B/A
also representing the effect of circular motion about A:
A B A B
A B A B
r v v
r v
/
/ /
+ =
=
e
e















A) Vector Analysis

1. Kinematics Diagram

- Establish the directions of the fixed x,y coordinates and draw a kinematics
diagram of the body
- Indicate v
A
, v
B
, e, r
B/A

- If magnitudes of v
A
, v
B
or e are unknown, the sense of direction can be
assumed

2. Velocity Equation

- To apply
A B A B
r v v
/
+ = e , express the vectors in Cartesian vector form and
substitute them into the equation.
- Evaluate the cross product and then equate the i and j components to obtain
two scalar equations.
- If negative answer obtained for an unknown magnitude, direction of vector
opposite to that shown on the kinematics diagram.

B) Scalar Analysis

1. Kinematics Diagram

- Draw a kinematics diagram to show the relative motion
- Consider body to be pinned momentarily at base point A, magnitude: v
B/A
=
e r
B/A

- Direction of v
B/A
established from the diagram

relative-position vector drawn
from A to B

angular velocity of the body

velocity of base point A

velocity of point B
Procedure for Analysis
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

63 |

2. Velocity Equation

- From equation v
B
= v
A
+ v
B/A
, represent each vectors graphically by showing
magnitudes and directions.
- Scalar equation determine from x & y components of these vectors.


See Example:







Exercise






























16.4 16.37 16.58 16.63
16.6 16.7 16.8 16.9
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

64 |

CHAPTER 17

KINETICS OF A RIGID BODY
(FORCE AND ACCELERATION)



Chapter Objectives
To introduce the methods used to determine the mass moment of inertia of a body
To develop the planar kinetic equation of motion for a symmetric rigid body
To discuss applications of these equations to bodies undergoing translation,
rotation about a fixed axis and general plane motion




17.1 Moment of Inertia


A body has a definite size and shape.
F = m.a (mass is a measure of the body resistance to acceleration)
Rotational aspect, caused by moment, M

M = Io where I moment inertia
- moment inertia is a measure of the resistance of a body to
angular acceleration (M = Io)

Moment inertia as the integral of the second moment about an axis of all the element of
mass, dm which compose the body.

dm r I
m
}
=
2


- moment arm, r perpendicular distance from z axis
- Value of I, different for each axis
- If material having variable density, , which dm = dV,
dV r I
V

}
=
2

- When being a constant,
dV r I
V
}
=
2





ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

65 |

Procedure for analysis.

For integration, consider only symmetric bodies having surface which are generated by
revolving a curve about an axis.










Shell element Dish element
- height, z, radius, r = y radius, y
- thickness, dy - thickness, dz
- dV = (2ty) (z) dy - dv = (ty
2
)dz


See Example:

- 17.1
- 17.2


Parallel Axis Theorem

If the moment of inertia of the body about an axis passing through the bodys mess centre
is known, then moment of inertia about any other parallel axis may be determined by
parallel axis theorem.















ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

66 |

Using Phythagorean theorem,

r
2
= (d + x)
2
+ y
2

Hence, moment of inertia,

} } }
} }
+ + + =
+ = =
m m m
m m
dm d dm x d dm y x I
dm x d dm r I
2 2 2
2 2
' 2 ) ' ' (
] ) ' [(






Where I
G
moment inertia about z axis passing through the mass center, G
m mass of the body
d perpendicular distance.


Radius of Gyration

Moment of inertia of a body about a specified axis, using the radius of gyration, k.

m
I
k mk I = = ,
2


Similarity between k & r, from dI = r
2
dm, moment of inertia of an elemental mass, dm of
the body about an axis.

Composite bodies

The body of constructed of a number of simple shape such as disk, spheres and rods, the
moment of inertia of the body about any axis, z can be determined by adding
algebraically the moment of inertia of all the composite shape.

+ = ) (
2
md I I
G


See Example:
- 17.3
- 17.4






I
G
zero through total mass, m
(since r
2
= x
2
+y
2
) mass
center
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

67 |


17.2 Planar Kinetic Equations of Motion

Limit of study planar kinetic to rigid bodies, which along with their loadings, are
considered to be symmetrical.




The inertial frame of reference x, y, z has its
origin coincident with the arbitrary point P in
the body. By definition, these axes do not rotate
and are either fixed or translate with constant
velocity.






Equation of translation motion.

- The external forces represent the effect of gravitation electrical, magnetic or contact force
between adjacent bodies.
- The analysis of a system of particles:
G
ma F

=
(the translation equation of motion far the mass centre of a rigid body)

- The sum of all the external forces acting on the body is equal to the bodys mass times
the acceleration of its mass centre, G
- For x-y plane,
y
G
y
x
G
x
a m F
a m F
) (
) (

=
=


Equation of rotational motion








Particle FBD Particle kinetic diagram
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

68 |

where : F
i
resultant external force
f
i
resultant internal force far I particle cause by interactions with adjacent
particle
m
i
mass of particle
a
i
instant acceleration

If moments of the force acting on the particle are summed about point P:

i i i i
a m r f r F r = +
or
i i i P
a m r M = ) (

The moment about P can be expressed in term of acceleration of point P.











If the body has an angular acceleration and angular velocity w,

) ( ) (
2
r r a r m M
p i i P
e o + =
) ( ) ( [
2
r r r r a r m
p i
+ = e o

Cross product operation with Cartesian component,

)]} ( [ ) ( ] ) ( ) [( ) {( ) ( yj xi k yj xi j a i a yj xi m k M
y P x P i i P
+ + + + + = o
k y x a x a y m
y P x P i
] ) ( ) ( [
2 2
o o + + + =

] ) ( ) ( [ ) (
2
r a x a y m M
y P x P i i p
o + + =

Letting m
i
dm,

o ) ) ( ) ( ) )( (
2
dm r a xdm a ydm M
m
y P
m
x P
m
p
} } }

+ + =

EM
P
represent only the moment of the external forces acting on the body about P.


ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

69 |

Note: the resultant of moment of the internal force is zero, since for the entire body, these
forces occur in equal and opposite collinear, thus the moment of each pairs of forces
about P cancels.


The integral of first and second term are wed to locate the bodys centre mass G

Since } y dm = m and } x dm = x m, and if point P coincides with the mass centre a for
the body, x = = 0,

o
G p
I M =

This rotational equation of motion state that the sum of the moment of all the external
forces computed about the bodys mass center G, is equal to the product of moment of
inertia of the body about an axis passing through G and the bodys angular acceleration.











=
P k p
M ) (
where
k
kinetics moment

When moments of the external force shown, on the free body diagram are summed about
point P, they are equivalent to the sum of the `kinetic-moments of the component of ma
G

about P plus the kinetic moment of I
G
o.

Equation of motion:

o
G
G
y G
y
x G
x
I M
a m F
a m F
=
=
=

) (
) (

or

=
P k p
M ) (





ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

70 |


17.3 Equation of Motion :Translation

When the rigid body undergoes a translation, all the particles of the body have the same
acceleration,


a
G
= a
o = 0

Rotational equation of motion applied at point G,
E M
G
= 0




Rectilinear translation:
All the particles of the body travel along parallel straight line path.












Since I
G
o = 0, only ma
G
on the kinetic diagram:

0
) (
) (
=
=
=

G
y G
y
x G
x
M
a m F
a m F










ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

71 |

CHAPTER 18

PLANAR KINEMATICS OF
A RIGID BODY:
WORK AND ENERGY



Chapter Objectives
To develop formulation for the kinetic energy of a body and define the various
ways a force and couple do work
To apply the principle of work and energy to solve rigid-body planar kinetics
problems that involve force, velocity and displacement
To show how the conservation of energy can be used to solve rigid-body planar
kinetic problems




18.1 Kinetic Energy

- Consider the rigid body shown with an arbitrary
ith particle of the body, having a mass dm, is
located at r from the arbitrary point P.
- If at the instant shown the particle has a velocity v
i
,
then the particles kinetic energy, T
i
= dm v
i
2

- Kinetic energy of the entire body:
}
=
m
i
v dm T
2
2
1


- In terms of velocity of point P,
j x v i j v
yj xi k j v i v
v v v
y p x p
y p x p
p i p i
] ) [( ] ) [(
) ( ) ( ) (
/
e e
e
+ + =
+ + + =
+ =


- Square of magnitude of vi:
2 2 2
2 2 2 2 2 2
2 2 2
) ( 2 ) ( 2
) ( 2 ) ( ) ( 2 ) (
] ) [( ] ) [(
r x v y v v
x x v v y y v v
x v y v v v v
y p x p p
y p y p x p x p
y p x p i i i
e e e
e e e e
e e
+ + =
+ + + + =
+ + = =




ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

72 |



- Substitute the equation of K.E.:

} } } }
+ + =
m m m
y p x p
m
p
dm r dm x v dm y v v dm T ) ( ) ( ) ( ) ( ) ( ) (
2 2
2
1
2
2
1
e e e






2
2
1
2
2
1
) ( ) ( e e e
P y p x p p
I m x v m y v mv T + + =

- For , 0 = = y x
2
2
1
2
2
1
e
G G
I mv T + =






- For a body which having either rectilinear or
curvilinear translation, e = 0,

2
2
1
G
mv T =








- Body has both translation & rotational kinetic energy:

2
2
1
2
2
1
e
G G
I mv T + =

- Note that v
G
= r
G
e,
2 2
2
1
) ( e
G G
I mr T + =



entire
mass m
of the
body
bodys center of mass G with
respect to P
bodys
moment of
inertia I
P

Translation
Rotation about a
fixed axis
moment of
inertia, I
o

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

73 |


2
0 2
1
e I T =






- Kinetic Energy:
2
2
1
2
2
1
e
G G
I mv T + =









18.2 The Work of a Force

a) Work of a Variable Force

}
=
s
F
ds F U u cos

where:

U
F
work done by force
F external force
s path
u - angle between the tails of the force
vector & the differential
displacement


b) Work of a Constant Force

s F U
C FC
) cos ( u =

where:

U
FC
work done by force
F
C
external force
S translation
u - angle of direction
General Plane
Motion
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

74 |


c) Work of a Weight


- undergoes a vertical displacement Ay
- upward direction negative work
(weight and displacement opposite
directions)

y W U
W
A =





d) Work of a Spring Force


) (
2
1 2
1
2
2 2
1
s k s k U
S
=

for
1 2
s s >

where:
k
s
= F
s
= spring force
s
1
= initial compression position
s
2
= further position


e) Forces That Do No Work

- act at a fixed points on the body or
having direction perpendicular to the
displacement
- refer to figure rolling resistance force
F
r
does no work since acting on a
round body as it rolls without slipping
over a rough surface
- due to F
r
acts at a point which has zero
velocity (instantaneous center, IC)
during any instant of time dt.
- work of F
r
= 0


See Example 18.1.

ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

75 |



18.3 The Work of a Couple

- when body translates positive work of one force
cancels the negative work of the other
- body undergoes different rotation du about an axis,
each force undergoes displacement ds
u
= (r/2) du
- total work done:

u
u
u u
d M
d Fr
d F d F dU
r r
M
=
=
+ =
) (
) ( ) (
2 2


- when body rotates through finite angle u (rad), work
of a couple:
}
=
2
1
u
u
u d M U
M


- for constant magnitude,

U
M
= M (u
2
- u
1
)

- work is positive for M and (u
2
- u
1
) are having the
same direction.

- See Example 18.2.




18.4 Principle of Work and Energy

= +
2 2 1 1
T U T










bodys initial translational & work done by all the external bodys final
rotational kinetic energy forces & couple moments translational &
rotational kinetic energy
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

76 |

Work of a weight Magnitude of work Vertical displacement
stretch / compression of
spring

spring stiffness


Procedure for Analysis

- Kinetic Energy (Kinematic Diagrams)
- translation -
2
2
1
G
mv T =
- rotation -
2
2
1
e
G
I T =
- special case (rotation about a fixed axis) -
2
0 2
1
e I T =
- use kinematic diagram determine v
G
, e and relationship between them


- Work (Free-Body Diagram - FBD)

- draw FBD count for all forces and couple moments
- integrate forces obtain work
- graphically work = area under force-displacement curve
- work of a weight:

U
W
= W y




- work of spring:

U
S
= k s
2






- work of couple product of couple moment and angle (rad) through which
it rotates
- work positive when force (couple moment) same direction as
displacement (rotation)


- Principle of Work & Energy

= +
2 2 1 1
T U T




bodys initial translational & work done by all the external bodys final
rotational kinetic energy forces & couple moments translational &
rotational kinetic energy
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

77 |


- See Example 18.2.

See Example:
- 18.3
- 18.4
- 18.5
- 18.6


18.5 Conservation of Energy





- Determine by knowing the height of
the bodys center of gravity
- Vg = W y
G

- P.E. positive when y
G
= positive







- Ve = + k s
2

- In deformed position, the spring force
acting on the body always has the
capacity for doing positive work when
spring is returned back to its original
undeformed position




Gravitational
Potential Energy
Elastic
Potential Energy
ENT142 ENGINEERING DYNAMICS
ZOL BAHRI RAZALI

78 |








- For body subjected to both gravitational and elastic forces,

Total P.E., V = Vg +Ve
or

Principle of work energy:
2 2 2 1 1 1
) ( V T U V T
noncons
+ = + +



For

, 0 ) (
2 1 noncons
U

2 2 1 1
V T V T + = + conservation of mechanical energy


Procedure for Analysis

- Potential Energy
- draw initial and final position diagram
- if center of gravity, G, performing a vertical displacement, establish a
horizontal datum to measure Vg.
- use V = Vg +Ve, where Vg = W y
G
(+/-),
Ve = + k s
2


- Kinetic Energy
- translation -
2
2
1
G
mv T =
- rotation -
2
2
1
e
G
I T =
- use kinematic diagram determine v
G
, e and relationship between them

- Conservation of Energy
-
2 2 1 1
V T V T + = +

See Example 18.7, 18.8 and 18.9.
Conservation of
Energy