Académique Documents
Professionnel Documents
Culture Documents
GIRD Systems CORDIC Tutorial
Transféré par
smbokhariCopyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
GIRD Systems CORDIC Tutorial
Transféré par
smbokhariDroits d'auteur :
Formats disponibles
http://www.girdsystems.
com
Using the CORDIC Algorithm for Fast Trigonometric Operations in Hardware
GIRD Systems Internal Seminar November 25, 2009
http://www.girdsystems.com
What is the CORDIC algorithm?
COordinate Rotation DIgital Computer Fast way to compute:
Magnitude and phase of a complex value Trigonometric functions such as sin and cos
Originally developed in 1959 for real-time aircraft navigation computer Computes values based on a series of rotations
http://www.girdsystems.com
Why use the CORDIC algorithm?
Major reason only multiplications required are bit shifts (simple in hardware) Multiplier units are resource hogs Iterative process more iterations yields better accuracy
Easy to trade off execution speed vs. accuracy Design to the constraints of the system
http://www.girdsystems.com
When to use CORDIC?
Any application that requires rapid calculation of trigonometric functions
Demodulation of successive carriers in OFDM symbols Rectangular-to-polar conversion operations
Especially useful for FPGA implementations with space constraints
CORDIC blocks are available from many manufacturers such as Xilinx
http://www.girdsystems.com
CORDIC Algorithm
Apply a series of rotations in the positive or negative direction Rotation is in increments of arctan(2-L) : L=0 45 L=1 26.565 L=2 14.036 L=3 7.125 Values can be precomputed and stored
http://www.girdsystems.com
CORDIC Algorithm
Mathematical view of the approach: Start with a complex value: C = Ic+jQc And a rotational value: R = Ir+jQr To add a rotation to C: C' = CR To subtract a rotation: C' = CR*
http://www.girdsystems.com
Adding a Rotation
For the CORDIC algorithm R = 1 + jK where K = 2-L Breaking out the equation for adding an equation: C' = CR Ic' = IcIr QcQr = Ic (Qc >>L) Qc' = QcIr + IcQr = Qc+ (Ic>>L)
Special case: Adding 90
R = 0 + j1 Ic' = -Qc Q c' = Ic
(negate Qc and swap)
http://www.girdsystems.com
Subtracting a Rotation
For the CORDIC algorithm R* = 1 - jK where K = 2-L Breaking out the equation for adding an equation: C' = CR* Ic' = IcIr + QcQr = Ic + (Qc >>L) Qc' = QcIr - IcQr = Qc - (Ic>>L)
Special case: Subtracting 90
R = 0 - j1 Ic ' = Qc Qc' = -Ic
(negate Ic and swap)
http://www.girdsystems.com
Computing sin and cos
Step 1: Start at Ic = 1 and Qc = 0 Step 2: Rotate in increments of 90 to move into the correct quadrant Step 3: Iterate over L, starting at L=0, until the desired accuracy is achieved. Add or subtract rotations so that the sum converges on the desired angle Ic = cos(b) Qc = sin(b)
http://www.girdsystems.com
Important Caveat
Since the magnitude of the rotation vector is not unity magnitude, we need to divide our results by a term called the CORDIC gain. CORDIC gain = prod(abs(1+j/2L),0,L) This term can be precomputed and stored L=0 Cg = 1.4142 1/Cg = 0.7071 L=1 Cg = 1.5811 1/Cg = 0.6325 L=2 Cg = 1.6298 1/Cg = 0.6136 Cg converges to approximately 1.647
http://www.girdsystems.com
Computing sin and cos A Simple Example
Find the sin and cos of 108.435 Start at 0 C = 1 + j0 Add 90 C = 0 + j1 Add 45 (L=0,b=135) C = (0-1) + j(1+0) = -1+j Subtract 26.565 (L=1,b=108.435) C = (-1 + 1/2) + j(1-(-1)/2) = -0.5 + j1.5 Divide by the CORDIC gain for L = 1, 1/Cg = 0.6325 sin(108.435) = 1.5(0.6325) = 0.9487 cos(108.435) = -0.5(0.6325) = -0.3162
http://www.girdsystems.com
Computing sin and cos Another Example
Find the sin and cos of 292.2 Start at 270 Add 45 (L=0, b=315) Subtract 26.565 (L=1,b=288.435) Add 14.036 (L=2, b=302.471) C = 0-j C = 1-j C = 0.5 - j1.5 C = 0.875 - j1.375
Subtract 7.125 (L=3,b=295.346)
Subtract 3.576 (L=4,b=291.767) Add 1.790 (L=5,b=293.560)
C = 0.703 - j1.484
C = 0.610 - j1.528 C = 0.658 j1.509
Subtract 0.895 (L=6,b=292.665)
Add 0.448 (L=7,b=292.217)
C = 0.635 - j1.520
C = 0.623 - j1.524
http://www.girdsystems.com
Computing sin and cos (cont.)
We are pretty close to 292.2, so we will stop here C = 0.623 - j1.524 Divide by CORDIC gain Ic = cos(292.217) = 0.623/1.64674 = 0.3781 Qc= sin(292.217) = -1.524/1.64674 = -0.9258 Compare to the actual values: cos(292.2) = 0.3778 sin(292.2 ) = -0.9259 Result will improve as more iterations are used
http://www.girdsystems.com
Matlab Code for Previous Example
beta = 270; phi = 292.2; C = 0-j; %initialize terms %precompute CORDIC angles num_iter = 7; angles = 180/pi.*atan(2.0.^[0:-1:-1*num_iter]);
for N = 1:length(angles)
L = N-1 if (beta < phi) beta = beta + angles(N) C = C*(1+(j/(2^(N-1)))) elseif (beta > phi) beta = beta - angles(N) C = C*(1-(j/(2^(N-1)))) end end % subtract rotation if beta > phi % print out L % add a rotation if beta < phi
Cg = prod(abs(1+j./2.^[0:length(angles)-1]))
C = C/Cg
%compute the CORDIC gain
%cos(beta) = real portion, sin(beta) = imaginary portion
http://www.girdsystems.com
Computing Magnitude and Phase
To compute magnitude and phase, we work backwards start with a complex value and rotate until the Q component is 0 and the I component is positive (i.e. 0 angle) Like sin and cos, magnitude and phase are computed simultaneously Again, we have to factor in the CORDIC gain when computing the magnitude
http://www.girdsystems.com
Computing Magnitude and Phase A Simple Example
Use CORDIC to estimate the mag. and phase of -1+j3 Since this number is in Quadrant II, we need to subtract 90to get back to Quadrant I: C = 3+j1 Now since I and Q are positive, we subtract the 45term: C = (3+1>>0) + j(1-3>>0) = 4-j2 Q is now negative, so we add the next phase term (26.57): C = (4-(-2)>>1) + j(-2+4>>1) = 5+j0 Now we are located on the real axis. The phase is the inverse of the sum of the rotations we applied: -1*(-90-45+26.57) = 108.43
http://www.girdsystems.com
Computing Magnitude and Phase A Simple Example (cont.)
To compute the magnitude, we take the real result and divide by the CORDIC gain Real result = 5 CORDIC gain for L = 1 is 1.5811 5/1.5811 = 3.162 Compare to the actual result abs(1+j*3) = sqrt(10) = 3.162
http://www.girdsystems.com
Computing Magnitude and Phase Another Example
Find the magnitude and phase for -3.84-j2.51 Add 180to move to Quadrant I : C = 3.84+j2.51
Subtract 45:
Add 26.565: Subtract 14.036:
C = 3.84+(2.51>>0) + j(2.51-3.84>>0) C = 6.35 - j1.33
C=6.35-1.33>>1+j(1.33+6.35>>1) C=7.02+j1.85 C=7.02+1.85>>2+j(1.85-7.02>>2) C=7.48+j0.09
Q term is almost zero, so we will use this approximation Phase = -1*(180-45+26.565-14.036) = -147.529 Magnitude = 7.476/1.630 = 4.5872 Compare to actual answer : 4.5876 @ -146.83
http://www.girdsystems.com
Summary
CORDIC is a fast way to compute trig functions and phase/magnitude in hardware
Almost no multiplication or division required other than bit shifts
Iterative process more iterations helps zero in on a more correct result CORDIC functions are available for FPGAs and the algorithm can be incorporated into other devices such as fixed point DSPs Good for resource constrained platforms, but computing values directly is more accurate if hardware is able to meet speed requirements
Vous aimerez peut-être aussi
- Advanced AutoCAD® 2017: Exercise WorkbookD'EverandAdvanced AutoCAD® 2017: Exercise WorkbookÉvaluation : 1 sur 5 étoiles1/5 (1)
- Control of DC Motor Using Different Control StrategiesD'EverandControl of DC Motor Using Different Control StrategiesPas encore d'évaluation
- ICA For G-3000Document107 pagesICA For G-3000AsgharPas encore d'évaluation
- Switching Power SupplyDocument138 pagesSwitching Power SupplyStephen Dunifer95% (22)
- PHD Thesis EricDocument143 pagesPHD Thesis EricsmbokhariPas encore d'évaluation
- Automatic Voltage RegulatorDocument35 pagesAutomatic Voltage Regulatoryousufswh100% (1)
- Projects With Microcontrollers And PICCD'EverandProjects With Microcontrollers And PICCÉvaluation : 5 sur 5 étoiles5/5 (1)
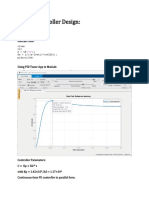
- Design of PID ControllerDocument13 pagesDesign of PID ControllershrikrisPas encore d'évaluation
- Master Microsoft Excel 2016 text functionsDocument14 pagesMaster Microsoft Excel 2016 text functionsratheeshPas encore d'évaluation
- Study of P, PD, Pi, Pid Controllers Using Mat LabDocument13 pagesStudy of P, PD, Pi, Pid Controllers Using Mat LabVignesh NagarajanPas encore d'évaluation
- David K. Cheng - Field and Wave ElectromagneticsDocument515 pagesDavid K. Cheng - Field and Wave Electromagneticsnikee7285% (26)
- Cement Process Engineering Vade-Mecum: 1. MathematicsDocument7 pagesCement Process Engineering Vade-Mecum: 1. MathematicsTamer FathyPas encore d'évaluation
- Signal Processing Algorithms for MIMO RadarDocument155 pagesSignal Processing Algorithms for MIMO RadarsmbokhariPas encore d'évaluation
- Brown Tonality and Form in Debussey PDFDocument18 pagesBrown Tonality and Form in Debussey PDFShawn SherwoodPas encore d'évaluation
- Greatest Common Divisor (Discrete Math)Document29 pagesGreatest Common Divisor (Discrete Math)api-33642484Pas encore d'évaluation
- CORDIC - Wikipedia, The Free EncyclopediaDocument7 pagesCORDIC - Wikipedia, The Free EncyclopediaJonjon JoneePas encore d'évaluation
- Roll Forming Handbook: George T. HalmosDocument6 pagesRoll Forming Handbook: George T. HalmosMarco Cruz67% (3)
- PD, PI, PID Compensation TechniquesDocument42 pagesPD, PI, PID Compensation TechniquesAsghar AliPas encore d'évaluation
- CordicDocument21 pagesCordic2015mdaamir2015Pas encore d'évaluation
- Implementing Sine and Cosine Using CORDIC AlgorithmDocument6 pagesImplementing Sine and Cosine Using CORDIC AlgorithmHarsh BaghelPas encore d'évaluation
- Aircraft Pitch - G1 ReportDocument79 pagesAircraft Pitch - G1 ReportTrabajo AviaciónPas encore d'évaluation
- Compensator Design II PDFDocument37 pagesCompensator Design II PDFMani Vannan SoundarapandiyanPas encore d'évaluation
- A Survey of CORDIC Algorithms For FPGA Based Computers: Ray AndrakaDocument0 pageA Survey of CORDIC Algorithms For FPGA Based Computers: Ray AndrakaCix XidPas encore d'évaluation
- DC DrivesDocument50 pagesDC DrivesjvilasisPas encore d'évaluation
- CORDICDocument8 pagesCORDICRofaelEmilPas encore d'évaluation
- Wan Amir Fuad Wajdi Othman Room: PPKEE 3.25 Ext: 6062 Email: Eeamirfuad@eng - Usm.myDocument11 pagesWan Amir Fuad Wajdi Othman Room: PPKEE 3.25 Ext: 6062 Email: Eeamirfuad@eng - Usm.myBruce ChanPas encore d'évaluation
- Automatic Voltage RegulatorsDocument35 pagesAutomatic Voltage RegulatorsAlejandroHerreraGurideChilePas encore d'évaluation
- Cordic by MohitDocument19 pagesCordic by MohitNarwal MohitPas encore d'évaluation
- Processcontrol Topic13 PidtuningDocument15 pagesProcesscontrol Topic13 Pidtuningmuthukumartharani100% (1)
- Modeling and Control of a Buck Converter in Ansoft SimplorerDocument25 pagesModeling and Control of a Buck Converter in Ansoft Simplorerc_u_r_s_e_dPas encore d'évaluation
- Controls Lab 2Document10 pagesControls Lab 2VIKAS JAATPas encore d'évaluation
- Controller Design Based On Transient Response CriteriaDocument20 pagesController Design Based On Transient Response CriteriaGapuk MaboekPas encore d'évaluation
- Least Cost System Operation: Economic Dispatch 2: Smith College, EGR 325 March 10, 2006Document37 pagesLeast Cost System Operation: Economic Dispatch 2: Smith College, EGR 325 March 10, 2006engidawabelPas encore d'évaluation
- PID and Feedback Compensation Design for Control SystemsDocument32 pagesPID and Feedback Compensation Design for Control SystemsNikhil PanikkarPas encore d'évaluation
- Ee 4314 ComphnvhvnDocument26 pagesEe 4314 ComphnvhvnSALIMSEIF1Pas encore d'évaluation
- AE421ADocument5 pagesAE421AShrutikirti SinghPas encore d'évaluation
- Activity 2Document7 pagesActivity 2Abderraouf HARCHEPas encore d'évaluation
- A.S.N Mokhtar - Implementation of Trigonometric FunctionDocument8 pagesA.S.N Mokhtar - Implementation of Trigonometric FunctionMohamed GanounPas encore d'évaluation
- Analysis of Simple CORDIC Algorithm Using MATLABDocument3 pagesAnalysis of Simple CORDIC Algorithm Using MATLABamit.18.singh2466Pas encore d'évaluation
- A MATLAB Script For Optimal Single Impulse De-Orbit From Earth OrbitsDocument20 pagesA MATLAB Script For Optimal Single Impulse De-Orbit From Earth OrbitsAnonymous REw1YIq4q7Pas encore d'évaluation
- MatLab ControllerDocument10 pagesMatLab ControllerPRONOJIT HUNTERPas encore d'évaluation
- Assignment 2 - Adv CTL 2020Document7 pagesAssignment 2 - Adv CTL 2020Thành Trung Nguyễn QuáchPas encore d'évaluation
- CORDICDocument32 pagesCORDICrah0987Pas encore d'évaluation
- Radix 8Document7 pagesRadix 8Loc LePas encore d'évaluation
- Clase Diseño Por Medio Del LGR Usando MatlabDocument42 pagesClase Diseño Por Medio Del LGR Usando MatlabJesus Tapia GallardoPas encore d'évaluation
- Improving The Euclidean AlgorithmDocument7 pagesImproving The Euclidean AlgorithmraulPas encore d'évaluation
- Frequency Response DesignDocument22 pagesFrequency Response Designمعروف المحجريPas encore d'évaluation
- Fuzzy Lab#1 Udara VER 2Document13 pagesFuzzy Lab#1 Udara VER 2Yudara AlmeidaPas encore d'évaluation
- Control de ProcesosDocument12 pagesControl de ProcesosLuis Fernando Pucuhuanca PachecoPas encore d'évaluation
- Root Locus DesignDocument10 pagesRoot Locus DesignirosenofPas encore d'évaluation
- Lecture 8: From Analog To Digital Controllers, PID Control Design ApproachesDocument10 pagesLecture 8: From Analog To Digital Controllers, PID Control Design ApproachesarafatasgharPas encore d'évaluation
- Advanced PID Controller ImplementationDocument13 pagesAdvanced PID Controller Implementationlizhi0007100% (1)
- Exercise:: Solution: Code: Part ADocument4 pagesExercise:: Solution: Code: Part AAbdul Rehman AfzalPas encore d'évaluation
- DC Motor Speed: Digital Controller Design: Eng Mohamed DobaDocument20 pagesDC Motor Speed: Digital Controller Design: Eng Mohamed DobaEng. Ibrahim Abdullah AlruhmiPas encore d'évaluation
- Cordic: (Coordinate Rotation Digital Computer)Document25 pagesCordic: (Coordinate Rotation Digital Computer)Magdalene MilanPas encore d'évaluation
- Cordic: (Coordinate Rotation Digital Computer)Document25 pagesCordic: (Coordinate Rotation Digital Computer)santhiyadevPas encore d'évaluation
- An Efficient VLSI Architecture For CORDIC AlgorithmDocument12 pagesAn Efficient VLSI Architecture For CORDIC AlgorithmAnonymous hh95x9VkPPas encore d'évaluation
- sc554 2014 Lecture09Document34 pagessc554 2014 Lecture09tharindu12Pas encore d'évaluation
- Orbital Mechanics MATLAB FunctionsDocument82 pagesOrbital Mechanics MATLAB FunctionsSnehalagoo LagooPas encore d'évaluation
- Engine Propeller Matching: Kelompok 1 Rega Ardian Syah Angga Wahyu P Pandika DarmawanDocument15 pagesEngine Propeller Matching: Kelompok 1 Rega Ardian Syah Angga Wahyu P Pandika DarmawanyuniardimzPas encore d'évaluation
- University of Basrah: Collage of Engineering Petroleum DepartmentDocument6 pagesUniversity of Basrah: Collage of Engineering Petroleum DepartmentNarjes WalidPas encore d'évaluation
- Field FormulasDocument39 pagesField FormulasKrishnaPas encore d'évaluation
- PID Algorithms (Topic 26)Document20 pagesPID Algorithms (Topic 26)MustaphaRamziPas encore d'évaluation
- L420 OpAmpCompIDocument14 pagesL420 OpAmpCompIShreerama Samartha G BhattaPas encore d'évaluation
- L100 MultistageFreq II (2UP)Document6 pagesL100 MultistageFreq II (2UP)Van Nguyen Huu VanPas encore d'évaluation
- Institute of Engineering Purwanchal Campus, Dharan-8Document12 pagesInstitute of Engineering Purwanchal Campus, Dharan-8Milan AcharyaPas encore d'évaluation
- Ben Salem Aymen 2014 ThesisDocument124 pagesBen Salem Aymen 2014 ThesissmbokhariPas encore d'évaluation
- Scheduling in The UMTS Enhanced UplinkDocument17 pagesScheduling in The UMTS Enhanced UplinksmbokhariPas encore d'évaluation
- LdpcphdhteissDocument333 pagesLdpcphdhteisssmbokhariPas encore d'évaluation
- E Book DSP Theory Ios Java Android Sim Final-REV-SPANIASDocument14 pagesE Book DSP Theory Ios Java Android Sim Final-REV-SPANIASsmbokhariPas encore d'évaluation
- Learning Material - ITCDocument96 pagesLearning Material - ITCKrishna SinghPas encore d'évaluation
- Array TheoryDocument17 pagesArray TheorysmbokhariPas encore d'évaluation
- Lecture Notes For Digital ElectronicsDocument43 pagesLecture Notes For Digital ElectronicsShruti GuptaPas encore d'évaluation
- Teaching With ScicoslabDocument11 pagesTeaching With ScicoslabsmbokhariPas encore d'évaluation
- Generating Function Analysis of Wireless Networks and ARQ SystemsDocument178 pagesGenerating Function Analysis of Wireless Networks and ARQ SystemssmbokhariPas encore d'évaluation
- Generating Function Analysis of Wireless Networks and ARQ SystemsDocument178 pagesGenerating Function Analysis of Wireless Networks and ARQ SystemssmbokhariPas encore d'évaluation
- Emerging Wireless Standards2Document114 pagesEmerging Wireless Standards2smbokhari100% (1)
- Thesis MatthiasDocument146 pagesThesis MatthiassmbokhariPas encore d'évaluation
- Viterbi 1971Document22 pagesViterbi 1971smbokhariPas encore d'évaluation
- Z-Transform - CH 7Document13 pagesZ-Transform - CH 7carmo-netoPas encore d'évaluation
- Bluetooth Mobile IpDocument57 pagesBluetooth Mobile IpMelissa ClarkPas encore d'évaluation
- 22.11.23293844 OFDM Based Cognitive Radio For DSA NetworksDocument205 pages22.11.23293844 OFDM Based Cognitive Radio For DSA NetworkssmbokhariPas encore d'évaluation
- New HARQ Scheme Based On Decoding of Tail-Biting Convolutional Codes in IEEE 802.16eDocument7 pagesNew HARQ Scheme Based On Decoding of Tail-Biting Convolutional Codes in IEEE 802.16esmbokhariPas encore d'évaluation
- WiMAX HandbookDocument39 pagesWiMAX HandbookwirelesssoulPas encore d'évaluation
- Open Verification Methodology: Fulfilling The Promise of SystemverilogDocument5 pagesOpen Verification Methodology: Fulfilling The Promise of SystemverilogsmbokhariPas encore d'évaluation
- X-Tel Hsdpa BrochureDocument2 pagesX-Tel Hsdpa BrochureAtcharao ThamballaPas encore d'évaluation
- 9829d23b-6e45-4cbd-b732-f870faff49a0Document6 pages9829d23b-6e45-4cbd-b732-f870faff49a0Swamy Dhas DhasPas encore d'évaluation
- Training Estimator by VladarDocument10 pagesTraining Estimator by VladarMohamad SyukhairiPas encore d'évaluation
- Bizhub 20 Service ManualDocument508 pagesBizhub 20 Service ManualSergio Riso100% (1)
- Operations Management Customer FocusDocument13 pagesOperations Management Customer FocusYusranPas encore d'évaluation
- GTU BE- Vth SEMESTER Power Engineering ExamDocument2 pagesGTU BE- Vth SEMESTER Power Engineering ExamBHARAT parmarPas encore d'évaluation
- Suzuki 660 K6aDocument88 pagesSuzuki 660 K6aJames Wayne BarkerPas encore d'évaluation
- C3Document14 pagesC3mee myyPas encore d'évaluation
- Field Technician UPS and Inverte - Question Bank.Document35 pagesField Technician UPS and Inverte - Question Bank.shruti borkarPas encore d'évaluation
- International Air Service Development at Boston Logan: June 7, 2012Document20 pagesInternational Air Service Development at Boston Logan: June 7, 2012chaouch.najehPas encore d'évaluation
- Brake Reaction Time MotorcycleDocument37 pagesBrake Reaction Time MotorcycleGeorge TsakatarasPas encore d'évaluation
- PCBA MachineDocument62 pagesPCBA MachineSahara MalabananPas encore d'évaluation
- Bab III.2.1. Generator Sinkron (Lanjutan)Document28 pagesBab III.2.1. Generator Sinkron (Lanjutan)Hariz AudirahmawanPas encore d'évaluation
- Problem Based Task Dfc2043Document3 pagesProblem Based Task Dfc2043player6675100% (1)
- Tips For Internship ReportDocument1 pageTips For Internship ReporthummayounnasirPas encore d'évaluation
- Schematic Diagrams: Compact Component SystemDocument12 pagesSchematic Diagrams: Compact Component SystemGustavo DestruelPas encore d'évaluation
- Samsung ML-1710 Recarga PDFDocument6 pagesSamsung ML-1710 Recarga PDFarkittoPas encore d'évaluation
- CIECO PPC1000R Installation Manual V3.3Document61 pagesCIECO PPC1000R Installation Manual V3.3TomPas encore d'évaluation
- Problems - SPCDocument11 pagesProblems - SPCAshish viswanath prakashPas encore d'évaluation
- AUC-Knowledge QuestionsDocument68 pagesAUC-Knowledge QuestionsFarhan SethPas encore d'évaluation
- 23 - Eave StrutsDocument2 pages23 - Eave StrutsTuanQuachPas encore d'évaluation
- Netsh Wlan Start HostednetworkDocument3 pagesNetsh Wlan Start HostednetworkM Nanda KumarPas encore d'évaluation
- TIMESHEETDocument5 pagesTIMESHEETWasKito AdyPas encore d'évaluation
- Humidifier Servo and Non Servo Mode of DeliveryDocument2 pagesHumidifier Servo and Non Servo Mode of DeliveryAlberth VillotaPas encore d'évaluation
- SRS Light IlluminatedDocument6 pagesSRS Light IlluminatedWadu DetutsPas encore d'évaluation
- Twingo 3 & Clio 4Document10 pagesTwingo 3 & Clio 4Alexandre Le GrandPas encore d'évaluation
- Document 1Document14 pagesDocument 1Lê Quyên VõPas encore d'évaluation