1

2012 JC2 Preliminary Examination

H2 Mathematics Paper 1
Solution

1
2
2
2 1
1
3
x x
x
+
<
+


2 2
2 1 3 x x x + < +

2
2 0 x x <

( 1)( 2) 0 x x + <

1 2 x < <



2 (i)
1 1
2
d 1
e e
d
x x
x x
=

(ii)
1 1
3 2
1 1
2
1 1
1 1 1
e d e d
1 1
e e d
1
e e
x x
x x
x x
x x
x x x
x
x x
C
x
| |
| |
=
| |
\ .
\ .
| | | |
| | | |
=
| | | |
\ . \ .
\ . \ .
= + +
} }
}




3
Distance between (1, 0) and (x, y), ( ) ( )
2 2
1 0 W x y = +
Since (x, y) lies on the curve, then
2
e
x
y =
Thus, ( ) ( )
2
2
2
1 e
x
W x = +
( )
2
2 4
1 e
x
W x = +
Differentiating w.r.t. x, ( )
4
d
2 2 1 4e
d
x
W
W x
x
= +
( )
4
d
When 0, 1 2e 0
d
x
W
x
x
= + =
From GC, x = 0.14043




2
x 0.14043
-
0.14043 0.14043
+
d
d
W
x

ve 0 +ve
\ /
Thus, W is minimum when x = 0.14043
When x = 0.14043,
2( 0.14043)
e 0.75513 y

= =
The coordinate of point P is (0.140, 0.755)

Alternative Method:
Curve ( )
2
4
1 e
x
y x = +

The x value of the minimum point of ( )
2
4
1 e
x
y x = + gives the
minimum value of ( )
2
4
1 e
x
x + .
When x = -0.1404361,
2( 0.1404361)
e y

= = 0.75513.
The coordinate of point P is (0.140, 0.755)


4
Let
n
P be the statement
( ) ( )
1
3
3 1 3 2 1
4
n
r n
r
r n
=
( = +

, n
+
e
When 1 n = , LHS =
( ) ( )
1
1
1
3 1 3 3
r
r
r
=
= =

RHS = ( ) ( )
1
3
1 3 2 1 1 3
4
( + =


Since LHS = RHS,
1
P is true.
Assume that
k
P is true for some k
+
e , i.e.
( ) ( )
1
3
3 1 3 2 1
4
k
r k
r
r k
=
( = +

To show
1 k
P
+
is true, i.e.
( ) ( ) ( )
1
1
1
3
3 1 3 2 1 1
4
k
r k
r
r k
+
+
=
( = + +

3
LHS =
( ) ( ) ( ) ( )
1
1
1 1
3 3 1 3
k k
r r k
r r
r r k
+
+
= =
= + +


= ( ) ( ) ( )
1
3
1 3 2 1 1 3
4
k k
k k
+
( + + +


= ( ) ( ) ( )
1
3 4
1 3 2 1 1 3
4 3
k k
k k
+ (
+ + +
(


= ( ) ( ) ( )
3
1 3 2 1 4 1
4
k
k k ( + + +


= ( )
3
1 3 6 3
4
k
k ( + +


= ( )
1
3
1 3 2 1
4
k
k
+
( + +


= ( ) ( )
1
3
1 3 2 1 1
4
k
k
+
( + +

= RHS

k
P

is true
1 k
P
+
is true
Since
1
P is true and
k
P

is true
1 k
P
+
is true,
by mathematical induction,
n
P is true for all n
+
e .


( ) ( ) ( )
2 2
1 1
2 3 3 2 3
n n
r r r
r r
r r
= =
=


( )
2 2
1 1
3 2 3
n n
r r
r r
r
= =
=


( )
( )
2
2
2 3 3 1
3
1 3 4 1
4 3 1
n
n
n

( = +



( ) ( )
2 2
3
1 3 4 1 3 3 1
4
n n
n ( = +





5 ln(cos2 ) y x =
d
d
y
x
=
2sin 2
2tan 2
cos 2
x
x
x

=
2
2
d
d
y
x
2
4sec 2x =
2
4(1 tan 2 ) x = +
2
1 d
4 1
4 d
y
x
| |
| |
= + |
|
|
\ .
\ .
2
d
4
d
y
x
| |
=
|
\ .



3
3
d
d
y
x

2
2
d d
2
d d
y y
x x
| |
=
|
|
\ .

4
4
d
d
y
x

2
2 3
2 3
d d d
2
d d d
y y y
x x x

| | | |

= +
| | `
| |
\ . \ .
)

When x = 0, y = 0,
d
d
y
x
= 0,
2
2
d
d
y
x
= 4,
3
3
d
d
y
x
= 0,
4
4
d
d
y
x
= 32

4
y = 4
2
2!
x
| |
|
|
\ .

4
32
4!
x
| |
|
|
\ .
+ =
2
2x
4
4
3
x
+

2
ln(sec 2 ) x =
2
1
ln
cos 2x
| |
|
\ .
=
( )
2
ln1 ln cos 2x = 2ln(cos2 ) x
=
2
4x +
4
8
3
x
+


6
(a)
(i)

2
2 5
2 3
x ax
y
x
+
=
+


( )
2
2
d 4 12 (3 10)
d
2 3
y x x a
x
x
+ + +
=
+

When
d
d
y
x
= 0,
2
4 12 (3 10) 0 x x a + + + =

For the curve to have no stationary points,
( )( )
2
12 4 4 3 10 0 a + <
1
3
a >


(ii)

2
2 5 2
1
2 3 2 3
x x
y x
x x
+
= =
+ +

Asymptotes: 1 y x = and
3
2
x =







(b)

( )
2
2
2
replace with
y
x
x x
=

+


3
2
x =

1 y x =

5
( ) ( ) ( )
( )
2 2 2
2 2 2
2 2 2
replace with 2
y y y
x x x
x x
= = =
+ +
+

2
2
replace with 2
y
x
y y
=
+

2
1
y
x
=
The curve before the transformation is
2
1
y
x
=

7 For any vectors a and b,
a b is perpendicular to both a and b
( ) ( ) 0 = = a a b b a b

Using Ratio Theorem,
= OD
2 2 1
3 3 3
a c
a c
+
= +
Normal vector of p: a b
line l:
2 1
( ) ( )
3 3
= + + r a c a b , e

Foot of perpendicular from D to p occurs at the point of intersection
between l and p

Vector equation of p: ( ) 0 r a b =

2
2 1
( ) ( ) 0
3 3
2 1
( ) ( ) ( ) ( ) 0
3 3
1
( ) 0 since ( ) 0
3
(
+ + =
(

+ + =
+ = =
a c a b a b
a a b c a b a b a b
c a b a b a a b


2
( )
3

=

c a b
a b
(shown)


8 (i)

d
, 0
d
x
kx k
t
= > ------- (1)

1
d 1 d x k t
x
=
} }

ln x kt c = +
e where e
kt c
x A A

= = ------- (2)

6
When
d
30, 5,
dt
x
x = =
From (1):
1
5 30
6
k k = =
When 0, 30, t x = =
From (2): 30 A =
Therefore,
6
30e
t
x

=

(ii)
When
1
3
2, 30e 21.5 t x

= = = ml

(iii) As , 0 t x .
Therefore, the amount of drug will eventually decrease to a limit of 0 ml.





6
30 e
t
x

=









9



6 z z = +
( )
( )
2
2 2 2
2
2
6
6
12 36 0
3
x y x y
x x
x
x
+ = + +
= +
+ =
=


















5
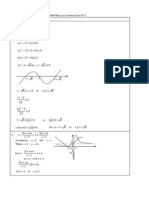
5
5
5 3
P
Q
30
t
x
7
1
3
arg cos 2.21
5
z

| |
= t =
|
\ .
or arg 2.21 z =
3 a = and 4 b =
Min 5i 34 4 w =
Max 5i 34 4 w = +



10
(a)
(i)
The amount saved by Sunny follows an AP.
a = 5, d = 2

Total amount saved by the end of nth week =
| | ( ) 2(5) ( 1)2 4
2
n
n
S n n n = + = +


(ii)
( )
2
4 1500 4 1500 0 n n n n + > + >
( ) 40.78 NA or 36.78 n n s >
Minimum number of week = 37 weeks


(iii) Amount saved by Starry follows a GP with a = 75, r = 0.95
Total amount saved by the end of nth month =
( )
( )
75 1 0.95
1500 1 0.95
1 0.95
n
n
n
S

= =

(iv) Since
75
S 1500
1 0.95

= =

which is the amount needed to buy the laptop, Starry will never be able to
save $1500 needed.


(b) Sequence is geometric

1
100, 1.1 T r = =
( )
( )
( )
( )
( )
100 1.1 1
1
1000 1.1 1
1 0.1
n
n
n
n
a r
S
r

= = =

4000
n
S >
( )
( )
1000 1.1 1 4000
n
>
( ) 1.1 1 4
n
>
( ) 1.1 5
n
>

8
( ) ln 1.1 ln5 n >
ln5
ln1.1
n >

16.89 n >

17 n = ie first exceeded $4000 on 17
th
birthday.



11
(i)
( )
| |
2
1 0
3
2 2
2 6
0
2

6
0
2

6
0

6
1 sin
d sin d
cos
tan d
(1 sec ) d
tan
3
3 6
x
x
x
u
u u
u
u u
u u
u u

=
=
=
=
=
} }
}
}




(ii)
When y =
2 3
,
3 2
x =
2
1
3
2
2
1 3 2
Area d
2 3
3 3
3 6 3
2 3
3 6
x
x
x

| |
= +
|
\ .
| |
= +
|
\ .
=
}


9
(iii)
2
2
2
1
3
2
2
2
1
3
4
2
1
4 2
3
2
1
3 1
3
2
1 2 3
Volume d
3 2
1 2 3
d
9
2 3
( ) d
9
2 3

3 1 9
2 4
3
3 27
x
x
x
x
x
x
x x x
x x


| |

| |
= + |
|
|
\ .
\ .

= +
= +
(
= +
(


(
=
(

}
}
}

4 a =


12
(i)
d d
2 , 2
d d
x y
t
t t
= =

At P,
2
, 2 x p y p = =
At P,
d 2 1
d 2
y
x p p
= =
Equation of normal at P is
( )
2
2 y p p x p =

(ii) At Q,

( )
2 2
2 2 q p p q p =
( ) ( )( ) 2 q p p q p q p = +
i.e.
2
q p q p
p
= =

(iii)

2 2
gradient of OP gradient of OQ 1
2 2
1
4
4 2
from (ii)
2
2
p q
p q
q
p
p
p p
p
p
p
=
=
=
=
=
=


10
(iv)

2
2
2
2
2
= ....(1)
2 4
4
Diff w.r.t
d d
2 4 ....(2)
d d
1
when 1, from (1)
4
d d
when 1, 0.1, 0.2 from (2)
d d
d d d
( )
d d d
1
(0.2) 1(0.1) 0.15 units / s
4
y y
x t
y x
T
y x
y
T T
y x
x y
y
T T
y x
xy x y
T T T
| |
= =
|
\ .
=
=
= =
= = =
= +
= + =