5.

1
ECE 410 DIGITAL SIGNAL PROCESSING A. Singer / D. Munson
University of Illinois Chapter 5 (part 3)


Convolution and unit-pulse response (u.p.r.)

Example

Find the unit pulse response [ ] h n for the system below.

z
1
z
1
x
n
y
n
3 1


y
n
= y
n1
+ x
n
+ 3 x
n1

For unit-pulse input with zero ICs have

h
n
+ h
n1
=
n
+ 3
n1
n 0, h
1
= 0

h
n
+ h
n1
= 0 n 2

But, need to find h
0
, h
1
:

h
0
= h
1
+
0
+ 3
1
= 1

h
1
= h
0
+
1
+ 3
0
= 2

For h
n
, n 2, solve

h
n
+ h
n1
= 0 n 2, h
1
= 2

Char. eqn: z + 1 = 0 root = 1

h
n
= c(1)
n

IC: h
1
= 2 = c c = 2

h
n
= 2(1)
n
n 1

Note that this solution holds for n 1 because the D.E. we were solving holds for n 2 and then
we forced the solution to hold at n = 1 by applying the IC.

Have h
n
= 0, n < 0 since started at zero initial state.
5.2

(Can check by iterating D.E. backward for zero IC with input = unit pulse)


0 0
[ ] 1 1
2( 1) 1
n
n
h n n
n
<

= =

>

The mechanics of discrete-time convolution are the same as for continuous convolution, except
have sums instead of integrals. Illustrate by examples.


Example

h
n
=
1
4
|
\
|
.
n
u
n


x
n
= u
n7


Find y
n
= h
n

*
x
n


Before solving, have a question.

Know

y
n
= h
m
x
nm
m

but why does x
n
have to be flipped around?

Consider

x
n
h
n
y
n

Which sample of x
n
{ } goes into the system first?

Answer: The n = 0 term! x
n
enters the system in the reverse order from how it is plotted. This
is why x
n
{ } must be flipped around when graphically computing a convolution.


Now, back to the convolution example. Have

5.3
y
n
= h
m
x
nm
m=0

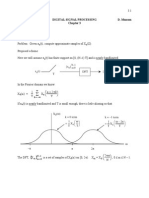
Note: Always draw pictures when working out a convolution. For our example we have:
-5 0 5 10
0
0.5
1
h[m] = (1/4)
m
u[m]
m
-5 0 5 10
0
0.5
1
x[m] = u[m-7]
m
7
-5 0 5 10
0
0.5
1
m
x[n-m] = u[n-m-7]
n-7


Case 1 n 7 < 0 n < 7

y
n
= 0

Case 2 n 7 0 n 7

y
n
=
1
4
|
\
|
.
m
m=0
n7

=
1
1
4
|
\
|
.
n6
1
1
4


=
4
3
1
1
4
|
\
|
.
n6



(

(





5.4
Example

x
n
=
1
0
2
0 0
n
n
n

| |

|
\ .

<

h
n
=
1
0
4
0 0
n
n
n

| |

|
\ .

<

y
n
=

0
1
4
m
m n m n m
m m
h x x

= =
| |
=
|
\ .

1 1
0

2 2
0 0 0
n m n m
n m
n m m n
x
n m m n

| | | |

| |
= =
\ . \ .

< >





n
m
x
nm
1
2
nm

Can always get x

nm
versus m
by flipping x
m
around origin and
shifting to right by n.


n < 0

y
n
= 0

n 0

y
n
=
1
4
|
\
|
.
m
m=0
n

1
2
|
\
|
.
nm
=
1
2
|
\
|
.
n

1
4
|
\
|
.
m
m=0
n

2
m
=
1
2
|
\
|
.
n

1
2
|
\
|
.
m
m=0
n

=
1
2
n
| |
|
\ .

1
1
1
2
1
1
2
n+
| |
|
\ .


= 2
2 1

1 1
2 2
n n+
(
| | | |
(
| |
\ . \ .
(

= 2
1 1 1
2 2 4
n n
(
| | | |
(
| |
\ . \ .
(


=
1 1
2
2 4
n n
| | | |
| |
\ . \ .

5.5

Example

x
n
= u
n
u
nN


h
n
= a
n
u
n


Find y
n
= h
n

*
x
n
via

a) Convolution formula

b) 1-sided z-transform method (applicable since both x
n
{ } and h
n
{ } are right-sided).

a) y
n
=
m=

x
m
h
nm


x
m
1
N1
m


a
nm
h
nm
n m

Case 1 n < 0

y
n
= 0

Case 2 0 n N 1

y
n
=
m=0
n

1 a
nm
= a
n

1
a
|
\
|
.
m
m=0
n

= a
n

1
1
a
|
\
|
.
n+1
1
1
a
=
a
n+1
1
a 1


Case 3 n N

y
n
=
m=0
N1

1 a
nm
= a
n

1
a
|
\
|
.
m
m=0
N1

= a
n

1
1
a
|
\
|
.
N
1
1
a


5.6
=
a
n+1
a
nN+1
a 1


Summarizing:

y
n
=
0 n < 0
a
n+1
1
a 1
0 n N 1
a
n+1
a
nN+1
a 1
n N









b) By Delay Property #1:

X(z) =
z
z 1
z
N

z
z 1


H(z) =
z
z a


Y(z) =
z
z a
z
z 1
z
N
z
z 1


(



Now, we are faced with a decision. We might consider writing

Y(z) =
z
z a
z z
1N
z 1



(

(
=
z
N
1
z
N2
(z a)(z 1)


However, a PFE of Y(z) will then have the form


Y(z)
z
=
A
1
z a
+
A
2
z 1
+
B
1
z
+
B
2
z
2
+
B
3
z
3
+ +
B
N1
z
N1


It looks like too much work to find the B
i
. Instead, note

Y(z) = Y(z) z
N
Y(z)

where

Y(z) =
z
2
(z a)(z 1)


Then, by Delay Property #1:
5.7

y
n
= y
n
y
nN
u
nN


Lets try this approach:


Y(z)
z
=
z
(z a) (z 1)
=
A
z a
+
B
z 1


A =
a
a 1
, B =
1
1 a


y
n
=
a
a 1
a
n
u
n
+
1
1 a
u
n


Now,

y
n
= y
n
y
nN
=

0 0
0 1

n
n n N
n
y n N
y y n N
>

=
1

1 1

0 0
1
0 1
1
1
n
n n N
n
a
n N
a
a a
n N
a
+
+ +

<

which agrees with our result obtained using the convolution formula.


Consider a 2-sided convolution.
Example h
n
=

step sequence
u
n1
x
n
=
1
3
|
\
|
.
n
n 0
4
n
n < 0







y
n
=
m=

h
m
x
nm
=
m=

u
m1
x
nm
=
m=1

x
nm



5.8
x
nm
=
1
3
|
\
|
.
nm
n m 0
4
nm
n m< 0





=
1
3
|
\
|
.
nm
m n
4
nm
m> n









n
m
4
nm

1
3
nm


n < 1

y
n
=
m=1

4
nm
= 4
n

1
4
|
\
|
.
m
m=1

= 4
n
1+
1
4
|
\
|
.
m
m=0

(

(


= 4
n
1+
1
1
1
4




(

(
(


=
1
3
4
n


n 1

y
n
=
1
3
|
\
|
.
nm
m=1
n

+
m=n+1

4
nm


=
1
3
|
\
|
.
n
1+ 3
m
m=0
n

(

(
+ 4
n

1
4
|
\
|
.
m
m=0

1
4
|
\
|
.
m
m=0
n

(

(


=
1
3
|
\
|
.
n
1+
1 3
n+1
1 3



(

(
+ 4
n

1
1
1
4

1
1
4
|
\
|
.
n+1
1
1
4





(

(
(
(


5.9
=
1
3
|
\
|
.
n

1
2
1
3
|
\
|
.
n
+
3
2
+
4
3
4
n

4
3
4
n
+
1
3



=
3
2
1
3
|
\
|
.
n
+
11
6



1
4 1
3
11 3 1
1
6 2 3
n
n n
n
y
n

<

| |

\ .



Example

h
n
=
0 0
1 1 5
1
6
2
n
n
n
n

| |

\ .


x
n
=
5 4
1
4
7
n
n
n
n

| |
>
|
\ .


y
n
= h
m
x
nm
m=

5.10
1
h
m
1 5 6
m

1
2
m
5
m
x
m
4
m
3

1
7
m

1
7
nm
5
nm
m
n + 4 n + 3
x
nm



Case 1 n + 4 1 n 3

y
n
=
m=1
5

1 5
nm
+
1
2
|
\
|
.
m
m=6

5
nm


=


Case 2 1 < n + 4 5 3 < n 1

y
n
=
m=1
n+3

1
1
7
|
\
|
.
nm
+
m=n+4
5

1 5
nm
+
1
2
|
\
|
.
m
m=6

5
nm


5.11

Case 3 n + 4 > 5 n > 1

y
n
=
m=1
5

1
1
7
|
\
|
.
nm
+
1
2
|
\
|
.
m=6
n+3

m

1
7
|
\
|
.
nm
+
1
2
|
\
|
.
m
m=n+4

5
nm


(Treat n = 2 as subcase of Case 3, where second sum is defined to be zero.)