vMathwise module: Higher Order Differential Equations

Worksheet topic: Predator-prey Model

Objective: To model a predator-prey relationship between two species using a system
of differential equations.
This worksheet should be studied in conjunction with learning unit 5: Phase
Plots of the Mathwise Module Higher Order Differential Equations
For general instructions on accessing and using Mathwise, see the appendix at the end of
this worksheet.
1. Derivation of the model
Mathwise
Learning unit 5: Phase Plots, section 4: Predator-prey model,
Study page 1
A predator-prey relationship between two species occurs when one species (the predator)
feeds almost exclusively on a second species (the prey).
Let x be the number of prey and y be the number of predators.
The standard Lotka-Volterra model is:
dx
dt
ax bxy
dy
dt
cy dxy

+

.................... (1)
where a, b, c and d are positive constants.
The model is derived by making the following assumptions:
In the absence of predators, the population of prey grows exponentially.
In the absence of prey, the number of predators decreases exponentially.
The number of prey is reduced at a rate proportional to the number of possible
interactions between prey and predators.
There is a corresponding increase in predators at a rate proportional to the number
of interactions.
2. Simulation
Mathwise
Learning unit 5: Phase Plots, section 4: Predator-prey model,
Study pages 2 - 3
Page 2 Investigate the population dynamics of the model:
dx
dt
px xy
dy
dt
y xy

+

.................... (2)
for at least four different values of the parameter p ( e.g. p = 0.5, 0.7, 1.0,
1.2, 1.5) as follows:
drag the slider to set a value for p
click start
when the graphs are complete, the message Do you wish to retain the results
for this simulation? is shown. Click yes.
drag p to a new value and repeat.
when you have stored the results for several values of p move to the next
page.
Page 3 The p values you used on page 2 are shown at the bottom right hand side of
the screen.
select the first p value to plot its phase path
repeat for the other p values
make a careful copy of the trajectories below and add the direction of travel
along each.
Phase paths of the predator-prey model
2
y
x
click continue to complete page 3.
To estimate the cycle length, go back to page 2 and set p = 1. The time
taken to complete one cycle can be estimated from the horizontal scale of
either graph.
3. Analysis
By analysing the phase portrait of a system we can predict the behaviour of the model
under different conditions. Some of the questions we might want to answer are:
Do there exist population levels p
x
and p
y
, say, at which the two species
coexist in a steady state ?
ie are there numbers p
x
and p
y
such that x(t) = p
x
and y(t) = p
y
is a solution
of (1).
Recall that points such as ( p
x
, p
y
), if they exist, are known as equilibrium
points (also called critical points) of the system. At an equilibrium point,.
dx
dt
dy
dt
0 0 and
Suppose the two species are coexisting in equilibrium. Then we add a few
members of species one to the microcosm. Will x(t) and y(t) remain close to
their equilibrium values or will the extra members give species one an advantage
so that it proceeds to annihilate species two ?
Mathwise
If you are unsure about the concepts of the phase plane, equilibrium points and
their stability, revise pages 1- 4 of Learning unit 5: Phase Plots, section 2: The
Phase plane, before proceeding with this worksheet.
Mathwise
Learning unit 5: Phase Plots, section 4: Predator-prey model,
Study pages 4 - 5
The equilibrium points of the standard Lotka-Volterra model (1) are:
and
Which equilibrium point is unstable?
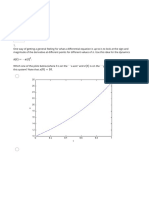
The phase plane plots on pages 4 and 5 show a typical closed trajectory of the predator-
prey model (2) with the parameter p = 1.5. By varying the initial population x and y,
we can see that, in all cases, the trajectory is a simple closed curve enclosing the
equilibrium point (1,1.5), as shown in the phase portrait below.
3
Phase portrait when p = 1.5
It can be shown that the trajectories of system (1) are closed curves for all values of a, b,
c and d. Thus, the equilibrium point
c
d
a
b
,

_
,
is a centre and all solutions of the system
are periodic for both x and y. This explains the fluctuations that have been observed
experimentally in predator-prey populations.
What is the predator population, y, when the prey population, x, is :
(a) maximal?
(b) minimal?
What is the prey population, x, when the predator population, y, is :
(a) maximal?
(b) minimal?
Using the phase diagram on page 5, deduce the following:
Is the prey population increasing or decreasing at a time when x = 3 and y = 1?
4
prey
predators
Is the predator population increasing or decreasing at a time when x = 0.5 and y = 3?
Is the predator population increasing or decreasing at a time when x = 2 and y = 3?
Explain, in your own words, why the prey population is declines in regions 3 and 4 of the
phase plot on page 5.
Mathwise
Learning unit 5: Phase Plots, section 4: Predator-prey model,
Do the exercise on page 6
4. Exercises
1. A Volterra predator-prey model is described by:
dx
dt
x xy
dy
dt
y xy

+
0 2 0 0025
01 0 002
. .
. .
where x and y are the populations of prey and predator, respectively, at time t.
Locate and classify the equilibrium points of the system.
2. Assume that populations of ladybirds (predators) and aphids (prey) in a certain
environment satisfy the predator-prey equations. An insecticide that kills some
fraction of each species (per unit time) is used to control the aphids. This system
is modelled by the equations:
dx
dt
ax bxy ex
dy
dt
cy dxy fy

+
where e and f are the respective rates at which the aphids and ladybirds are killed
by the insecticide.
(a) Find, by comparison with the standard model, the non-zero equilibrium point in the
first quadrant.
5
(b) Under what harvesting conditions (i.e.values of e and f) will the equilibrium stock
of prey increase whilst the equilibrium stock of predators decreases?
(c) It can be shown that the average level of each population over one cycle equals its
equilibrium value. Describe the effect of the use of
(i) an insecticide which destroys both ladybirds and aphids;
(ii) an insecticide which destroys aphids only.
3. Consider two species each of whose survival depends on their mutual cooperation.
An example would be a species of bee that feeds primarily on the nectar of one
plant species and simultaneously pollinates that plant. One simple model of this
mutualism is given by the autonomous system:
dx
dt
ax bxy
dy
dt
my nxy
+
+
(a) What assumptions are implicitly being made about the growth of each species in
the absence of cooperation?
(b) What are the equilibrium points of this system? Analyse their stability.
(c) Sketch the phase portrait. Hence, deduce the conditions under which
(i) both populations become extinct;
(ii) both populations grow and flourish.
5. Additional reading
Further analyses of the predator-prey and related models can be found in the
following books:
Differential Equations with Boundary value problems, Zill & Cullen, PWS-Kent,
1993, ch. 10.4
Differential Equations and Boundary value problems, Edwards & Penney,
Prentice-Hall, 1996, ch.6.3.
Modelling with Differential Equations, Burghes and Borrie, Ellis Horwood,
1982, ch.7.2
6
Answers to exercises
1 (0,0) saddle point (50,80) centre.

2. (a)
c f
d
a e
b
+

_
,

,
(b) f > 0 and 0 < e < a

(c)(i) If e < a, then the equilibrium number of ladybirds will decrease and the
equilibrium number of aphids will increase;
(ii)Equilibrium number of ladybirds will decrease whilst equilibrium number of
aphids remains unchanged (since f = 0).
3(a) In the absence of cooperation, both species decline exponentially.
(b) Equilibrium points are (0,0) - stable node and (7.5, 10) - saddle point
(c)
(i) x < m/n and y < a/b
(ii) x > m/n and y > a/b
7
10 20
10