1

MINISTRY OF SCIENCE AND TECHNOLOGY

DEPARTMENT OF TECHNICAL AND VOCATIONAL EDUCATION

AR 01012 DESCRIPTIVE GEOMETRY -I

A.G.T.I (First Year)

Architecture

TABLE OF CONTENTS Introduction Chapter I Tools and Equipment 1.1 General introduction 1.2 Lists of Equipments and tools 1.2.1 Drawing board 1.2.2 T- square 1.2.3 The Compass 1.2.4 The Divider 1.2.5 The Triangle 1.2.6 The Pencils 1.2.7 The Template 1.2.8 The Curve 1.2.9 The Eraser 1.2.10 The Erasing shield 1.2.11 Suggestion to keep drawing clean 1.3 Scale Geometric construction 2.1 Purpose 2.2 Definitions and terms 2.3 Method of construction for some basic geometric construction 2.3.1 Project (1) GEOMETRIC CONSTRUCTION 2.3.1.1 Bisecting a line 2.3.1.2 Bisecting an acute angle 2.3.1.3 Constructing a line parallel with a given line 2.3.1.4 Constructing a perpendicular to a line from a point not on a line 2.3.1.5 Dividing a straight line into equal parts 2.3.1.6 Locating tangent points 2.3.1.7 Constructing an angle from a given angle 2.3.1.8 Constructing a circle throught three given points 2.3.1.9 Constructing an ogee curve 2.3.2 Project (2) REGULAR POLYGON 2.3.2.1 Hexagon with 30/60 Triangle 2.3.2.2 Constructing of regular Hexagon with distance across corners given 2.3.2.3 Constructing a regular Hexagon with length of side given 2.3.2.4 Constructing a regular hexagon inscribe in a circle of distance across corners given 2.3.2.5 Constructing a regular Pentagon with inscribe in a circle of given radius 2.3.2.6 Subdivision into 5 parts 2.3.2.7 To draw a circle of radius r tangent to two other circles (a) Tangent externally (b) Tangent internally

Chapter II

Project (3) ELLIPSE & SPIRALS 2.3.3.1 Two circles or projection method 2.3.3.2 Focal distance method 2.3.3.3 Four center approximate method 2.3.3.4 Isometric circle 2.3.3.5 Constant pitch spiral 2.3.3.6 Ionic volute spiral 2.3.4 Project (4) PARABOLA & HYPERBOLA 2.3.4.1 Parabola 2.3.4.2 Hyperbola Chapter III MULTI-VIEW DRAWINGS 3.1 Purpose 3.2 Basic principle 3.3 Third angle projection 3.3.1 Selected and placement of views 3.4 Dimension 3.4.1Purpose of dimension 3.4.2 Type of dimensioning systems 3.4.3 Basic dimensioning concepts 3.4.4 Dimension line 3.4.5 Extension line 3.5 Projects

2.3.3

6 INRRODUCTION GEOMETRY AND GRAPHIC FOR ARCHITECTS AND BUILDING ENGINEERS PREFACE Geometry and Graphic training that is suitable for the student of Art and engineering. For the Architect, the geometric construction of surfaces and graphic presentation are of great importance in designing and presenting the building. This book illustrates the application of geometry and graphic to the building design. The standard/ examples of geometric construction of planes and surfaces, multi-view drawing, development, descriptive geometry and pictorial drawings are collected for architectural students.

7 CHAPTER I TOOLS AND EQUIPMENTS 1.1 General introduction Definition- Geometric construction and Graphic presentation is the language. By which we can express any information of our design. Limits of Accuracy- in geometry a point is defined, as having position, but not magnitude, and a line has no breadth. A point, pricked in the paper with the point of a needle, need not be more than 1/200 of an inch in diameter. A line drawn with a lead pencil need not be more than 1/200 of an n inch wide, and with a good 'straight-line'. 1.2 Lists of Equipments The following drawing instruments and supplies are typical of those used by architects and engineers and drafters. 1. Drawing board (imperial size, 30"x22") 2. T-square or parallel ruler 3. Set-square/ 45 deg. Triangle (8" to 10") 4. Set-square/ 30-60 deg. Triangle (10" to 12") 5. Scales (Architectural) 6. Eraser 7. Tape, 1/2" roll 8. Erasing shield 9. Sanding pad 10. Leads (6H,4H ,2H,H,F, HB) 11. Compass (6" to 8") 12. Divider 13. Irregular curve 14. Drafting brush 15. Protractor

1.2.1Drawing board Drawing boards vary greatly in size from small ones which can be conveniently carried around, say 12 by 15, to large vertical boards 6 or 7 feet high by 10 or 12 feet long. Regardless of size, the surface should be free from cracks and it should be a plane. Soft white pine or bass wood is a most suitable material since this will take thumb tacks or other fasteners. At least on edge should be straight as a base for the T-square.

8 1.2.2 T-square The common T-square consists of two parts, the blade and the head, which should be rigidly fastened together. A variety of kinds and sizes may be obtained from the trade. Different lengths may be obtained, ranging from 18 to 72. The straightness of the blade may be tested by drawing a straight line between two points and them turning the blade over and drawing a line between the same two points, using the same edge as before as shown in fig (1). If the blade is true, the two lines will coincide.

Fig. (1) Testing the T- square 1.2.3The Compass

Fig (2) Direction of ruling with T-square and triangle

The compass is used to draw circles and arcs. Compasses can be used for both ink and lead work and are available in various sizes and styles to meet different drawing requirements. The Bow Compass The center wheel adjustment bow compass is the compass most commonly used in drafting laboratories. Adjustment by means of the center wheel allows the drafter to set the particular arc or radius to be drawn and ensures that the setting will not move out of adjustment until a readjustment is required. This type of compass and its use are demonstrated in Fig (3).

Fig (3) How to use a center wheel adjustment bow compass.

9 The Beam Compass A tool not used very frequently is the beam compass. The purpose of the beam compass is to draw large circles and crcs that cannot be drawn with a bow compass. This compass includes a bar and two movable point assemblies to secure lead, points, or a pen and must be positioned using both hands, as shown in Fig (4).

Fig. (4) Producing a large arc using a beam compass 1.2.4 The Dividers The dividers are similar in construction to bow compass except that the lead end of the compass is replaced with an additional metal point, as pictured in Fig(5). Dividers are used for transferring measurements, dividing lines, and laying out series of equal distances required in geometric construction, in descriptive geometry, or on development drawings.

Fig. (5) Use of dividers 1.2.5 The Triangle The drafter normally uses three types of triangles: the 45-degree triangle, the 30/60-degree triangle, and the adjustable triangle, all of which are shown in Fig (6). Triangles are manufactured in different sizes, are made of plastic, and are available in clear or colored material. Used individually, the 45-degree and 30/60-degree triangles allow one to draw lines at 30, 45, 60, and 90 degrees from the horizontal. When used together, however, they can prodice additional angles of 15 and 75 degrees, as illustrated in Figure (7). The adjustable triangle includes a protector so that any angle in one-half-degree increments can be obtained between 0 and 90 degrees. An adjusting nut allows the drafter to firm up the desired angle before use.

10 Fig. (9) shows the proper method for drawing angled lines using a triangle.

Fig (6) (a) Adjustable triangle Fig (7) Drawing 15-degree and 75- degree angles (b) 45 degree triangle (c) 30/60 degree triangle using two triangles with a straightedge or T square

Fig (8) Direction of drawing inclined lines.

Fig (9) Proper method for drawing angle lines.

1.2.6 Pencils Special pencils are used for drawing. They are of uniform size, hexagonal in shape, with varying size of lead as shown in Fig. Eighteen degrees of hardness are supplied by the manufacturer, ranging from 7B, the softest and blacket in the order shown in the figure, to 9H which is the hardest and produces a thin gray line. For general layout work in drawing, the 4H and 5H pencils are most useful, and harder varieties are used in graphic statics and other graphical computation methods where fine lines and extreme accuracy are required. For making a finished pencil drawing the H and 2H are more desirable since they give a sharp black line. For sketching and art work, the softer grades are used. The draftsman should learn to choose the quality of pencil appropriate to the work he has in hand.

11

Fig (10) 1.2.7 The Template Templates are widely used by drafting laboratory personel. A template is a thin (usually 1/32 to 1/16 inch thick) plastic aid for producing technical drawings. It is a time-saving device that allows rapid and accurate drawing of shapes and forms which are difficult to produce by other methods or tools. Many types of templates are available for drawing circles, ellipses, electronic symbols, logic symbols, architectural symbols, svtew threads, hardware, and specialty building trade items. When using a flat template (without nibs or standoffs to keep it away from the drawing), one shouel be careful to life the template after drawing each symbol or character. In order to keep the drawing surface clean, co not slide the template along the drawing surface. When inking, wait for the ink to dry before lifting or moving the template. Fig. (11) illustrates how to use a template.

Fig (11) How to use a circle template

12

1.2.8 The Curve Curves are used to draw irregular or noncircular shapes which are frequently required in producing development, ellipse-, parabola-, and hyperbola- type drawings. They are oftenreferred to as French curves or irregular curves. Curves are available in several different shapes and sizes (see Fig 12) and are capable of producing an unlimited number of irregular shapes. Curves are used to produce curved lines which cannot be drawn with a compass or template. Curves are thin plastic devices which are produced in clear or colored tones. The curve is normally used to draw a shape which is determined by a series of plitted point locations. The curve is used to connect the plitted points with a line, as shown in Fig (13).

Fig. (12) Irregular curves 1.2.9 The Eraser

Fig. (13) Curve drawn from plotted points

The eraser is used for amking corrections and changes in technical drawings. There are penciltype erasers, block-types erasers, soft and hard erasers, white and pink erasers, and plastic erasers. It is common practice to use a soft eraser to eliminate unwanted pencil lines. Hard erasers seem to contain a lot of grit which may tend to cause severe damage to the surface of the drawing medium. Vinyl erasers are suggested for use on a polyester film base medium.

1.2.10 The Erasing Shield The erasing shield is an ultra-thin piece of metal, in erasing segments of lines, arcs, or circles. The shield is used by placing it over the line segment to be erased; it should be held firmly in place. Care should be taken not to erase too hard or a hole through the medium may result. The use of an erasing shield is demonstrated in Fig (14).

13

Fig. (14) Use of erasing shield

1.2.11The following suggestions, if observed, will help to keep the drawing clean: a. In moving the T-square, bear down on the head so that the blade is raised slightly from the paper. b. The hands are always somewhat oily-keep them off the paper. c. Use a hard pencil for layout work. d. Pick up the triangles rather than slide them. e. When finishing a drawing with a soft pencil, cover all views, except the one you are working on, with a clean sheet of paper. f. Blow graphite particles, which flake off the soft pencil, from the sheet. g. Use the brush or soft cloth to brush erasing crumbs off the sheet rather than the flat of the hand. h. Use a hard smooth-surfaced paper if this is suitable for the type of drawing being made. i. Use of a finely ground cleansing material on the drawing during work will keep both the drawing and instruments clean. Several varieties of this material may be purchased. Although some draftmen use the ruling pen for lettering, this is not a good practice. The regular pen holder with pen points similar to those used in writing should be used. 1.3 SCALE Most measurements on architectural drawings are made with the architects scale. Scales are made of wood, plastic, or wood laminated with plastic. Sharp edges and distinct, machine-divided markings on the scale are necessary for accurate measurements. Scales are usually flat or triangular in shape and are available in 6, 12 and 18 lengths, with the triangular-shape 12length being the most popular. The triangle scale has an advantage over the flat scale in that it has six surfaces. Architect's scale is inch-foot scale. Listed below are the 11scales found on the triangular architects scale? Full scale, Full Size = 1:1 11/2= 1-0 = 1, Half Scale, Half Size = 1, Quarter Scale, One-fourth Scale 1/8= 1-0, One-Eight Scale 3/4= 1-0 3/8= 1-0 3/32= 1-0 3/16= 1-0

14 3= 1-0 Two different scales are combined on each face except the full-size scale, which is fully divided into sixteenths. The combined scales are compatible; one is twice as large as the other and their zero points and extra-subdivided units are on opposite ends of the scale. The extra unit near the end of the scale is subdivided into twelfths of a foot or inches, as well as fractions of inches on the larger scales. Accuracy in using the scale when preparing drawings is extremely important. To measure correctly with the scale, select the proper scaling edge and place it on the drawing with the edge parallel and slightly below the line to be measured. First, count from zero the full number of feet in the dimension, and using a sharp pencil make a dash with a non-print pencil at right angles to the scale; then count the inches (if the dimension has both feet and inches) from the same zero in the opposite direction on the scale and mark the other limit of the dimension.

15 CHAPTER II GEOMETRIC CONSTRUCTION 2.1 Purpose The geometric construction forms the basis for all technical drawings. The purpose of the geometric construction is to accurately developed plane geometric shapes ranging from squares, triangles, and three-dimensional cylinders to complex irregular curves and ellipses. These constructions are normally produced without the aid of a scale, but rather with simple drafting tools. Engineers, designers, and drafters regularly perform the task of producing geometric constructions in their work, applying the principles of plane geometry. The process involved in the production of geometric constructions requires a basic understanding of plane geometry. Geometric construction skills can be acquired and demand precision and the correct use of drafting instruments. In developing geometric constructions it is important that drafting tools be in good repair. 4H to 6H leads are normally used for constructions that produce very lightweight lines. These lines need not necessarily be erased when the construction is completed. A small error or inaccuracy in the solving of a geometric problem could result in a serious error in the final construction.

2.2 DEFINITIONS OF TERMS Line A mark drawn with a pencil or pen, in any direction. A straight line is the shortest distance between two points. Lines may be drawn thin or thick depending on the application, as shown in Fig. (a). Point A precise position in space whose location is normally shown as an intersection of two very short lines. A dot may ne used as a temporary point Location. A crosshair is preferred, as illustrated in Fig(b). Angle The space that is formed thin two lines originating at a common point. There are three types of angles: the acute angle, whose space occupies less than 90 degrees; the right angle, whose space occupies exactly 90 degrees; and the obtuse angle, whose space occupies more than 90 degrees. Illustrations of each are shown in Fig(c). Circle A closed plane curve in which all points are at an equal distance from the center. A circle contains 360 degrees. An arc is a segment of a circle. Each is illustrated in Fig (d). Triangle A closed plane figure having three sides and three interior angles. A triangles three angles always total 180 degrees, as depicted in Figure 5.1(e). Commonly used traingles are shown in Fig(f).

16 Polygon A closed plane figure having three or more straight sides. A regular polygon is a figure whose sides are all equal in length. Common polygons include the triangle, the square, the pentagon, the hexagon, the septagon, the octagon, the nonagon, and the decagon. Fig(g) represents the eight commonly used regular polygons. Quadrilateral A polygon with four sides. FOur types whose opposite sides are parallel, which identifies each as a parallelogram, are depicted in Fig(h). Ellipse A closed symmetrical curve theat resembles a flattened circle. It is formed by a point moving so that at any position the sum of the distances from two fixed points (foci) is a constant (equal to the major diameter). The terms minor diameter, major diameter, minor radius, and major radius are used when producing an ellipse. Very often ellipses are required to represent circles, wholes, and round areas on oblique, isometric, and inclined surfaces. It is the drafters responsibility to see that the ellipse is constructed correctly.Fig (i ) shows a typical ellipse. Perpendicular The meeting of a given line or surface at exactly right angles (90 degrees) with another line or surface. Fig(j) illustrates two lines meeting at 90 degrees. Tangent A line or curve that touches (without crossing) at a single point of a circle or an arc. Examples are represented in Fig.(k). There are a number of basic geometric constructions with which the drafter should be familiar. The beginning drafter should follow the basic sequence in each illustration that follows the learn how to develop the various geometric forms. In each of the examples there is given information that is basic to the solution.

17

18 2.3 METHOD OF CONSTRUCTION FOR SOME BASIC GEOMETRIC CONSTRUCTION 2.3.1 PROJECT (1) GEOMETRIC CONSTRUCTION 2.3.1.1 Bisecting A Line Given: Line AB Step 1: Using points A and B as center points for radii, set radius on compass greater than one-half of AB. Strike radius AC and radius BD. Step 2: Draw a straight line through points C and D. Line CD bisects EAB and is called the perpendicular bisector because it forms an exact 90 degree angle with line AB.

Fig. (15) Procedure for bisecting a line 2.3.1.2 Bisecting And Acute Angle Given: Acute angle ABC Step 1: Set compass point at B, and produce radius BD so that it crossed BC and BA at points E and F. Step 2: With the compass, strike equal arcs from pointsE and F whose radius r is greater than onehalf of the distance AC. Make certain that the arcs intersect at G. Step 3: Draw a straight line through B and G. BG bisects angle ABD, producing two equal angles,ABG and CBG.

19

Fig. (16) Procedure for bisecting an acute angle 2.3.1.3 Constructing A Line Parallel With A Given Line Given: Line AB in Figure 5.5. Step 1: Place compass point on line AB, closer to point A than to point B. Strike any convenient radius r. Step 2: Using the same radius r, strike a second radius from a point closer to point B on line AB. Step 3: Draw a straight line through the tangents (high points) of both radii r. The resulting line CD is parallel to line AB.

Fig. (17) Procedure for constructing a line parallel with a given line 2.3.1.4 Constructinga Perpendicular To A Line From A Point Not On The Line Given: Line AB and random point P in FIgure 5.6. Step 1: Using point P as the center, strike a convenient radius r to intersect line AB at points C and D.

20 Step 2: Strike two equal arcs significantly greater than r, from points C and D so that they intersect each other at point E. Step 3: Draw a straight line from point E through point P and extend it until it touches line AB. This line is perpendicular to line AB, which means that it forms a 90-degree angle with line AB.

Fig. (18) Procedure for constructing a perpendicular to a line from a point not on the line. 2.3.1.5 Dividing A Straight Line Into Equal Parts Given: Straight line AB in Fig (19), to be divided into five equal parts. Step 1: Draw line BC perpendicular to AB. Step 2: Place a 0 at point A. Place a scale at the 0 point and pivot the scale until the five-inch point on the scale crosses line BC. Place short vertical dashes at the one-, two-,three-, and four-inch marks on the scale on the five-inch-long line. Identify these inch marks as 1,2,3, and 4, and place a 5 at point C. Step 3: Project lines downward from the points marked 1,2,3, and 4 to cross line AB, making certain they are parallel to BC. The original line AB has now been divided into five equal parts. This method can be used to divide a line of any length into the desired number of equal parts.

Fig. (19) Procedure for dividing straight line into equal parts

21 2.3.1.6 Locating Tangent Points The method for determining tangent points is essentially the same for the right angle, the acute angle, and the obtuse angle. The procedure outlined below, and illustrated in FIgure 5.12, is for constructing an arc tangent to a right angle. Given: Tow lines AB and BC, which are at right angles to each other, and radius r (see Figure 5.12). Step 1: Extend the compass to the length of the given radius, r. Strike this radius twice from line AB and twice from line BC, as shown. Step 2: Draw a straight line across the tangent (high) points of the arcs from line AB. Do the same with the arcs from line BC. Step 3: The point of intersection O of the two lines drawn across the tangent points of the arcs is the center for the radius that will be tangent to the right angle formed by lines AB and BC.

Fig.(20) Procedure for locating tangent points. 2.3.1.7 Constructing An Angle From A Given Angle Given: Angle ABC formed by two straight lines that meet at B, and radius r, which intersects BA at G and BC at F. These are shown in FIgure 5.8. Step 1: Draw line DE equal in length to line BC. Using a compass, strike given radius r from point D so that it crosses DE. Identify point H on line DE. Step 2: Using a compass on the given figure, place compass point at F and strike an arc at G. Transfer arc FG to the figure where the angle is to be transferred. It will become arc HJ. Step 3: Draw a straight line through DJ. Angle JDH is equal to angle ABC.

22

Fig.(21) Procedure for constructing an angle from a given angle. 2.3.1.8 Constructing A Circle Through Three Given Points Given: Three randomly located points A, B, and C Step 1: Draw a straight line through points A and B and another straight line through points B and C. Step 2: Using the method for bisecting a line in Figure 5.2, bisect lines AB and BC. Extend bisectors until they intersect at point O. Point O is the center of the intended circle. Step 3: Set compass point at O and strike radius OA, OB, or OC, which would all be equal in length. Complete radius until a full circle is formed.

Fig.(22) Procedure for constructing a circle through three given points.

23

2.3.1.9 Constructing An Ogee Curve An ogee curve, which is also referred to as a reverse S-curve, is used to connect two parallel lines. This construction practice is used in determining bends in pipes and curvatures in rail and road construction. Given: Two parallel lines AB and CD offset from each other, as shown in Figure 5.13. Step 1: Draw a straight line through points B and C. Construct the perpendicular bisector of line BC to establish point O. Step 2: Construct perpendicular bisectors of lines BO and CO. Step 3: Construct perpendicular at point B to intersect with the perpendicular bisector of line BO. This intercept is point E. Construct a perpendicular at point C to intersect with the perpendicular bisector of line CO. This intercept is point G. Step 4: With the compass point at E, strike radius EB. Radius EB should be tangent to line AB and should cross line BC at point O. Radius EB is the same as radius FC. Set compass point at F and strike radius FC. This completes the ogee curve.

Fig.(23) Procedure for constructing an ogee curve.

24

To Connect Two Straight Parallel Lines by a Reverse Curve at Fixed on the Lines By Equal Arcs. (fig a)

Fig. (24) Connecting straight lines by a reverse curve. Step 1- Connect by a straight line the points A and B at which the curve is to begin and end. Step 2Bisect AB, and then erect a perpendicular bisector of each half until they intersect

the perpendiculars to the original lines drawn at A and B. These intersections C and D are the centers of the two arcs. By Unequal Arcs, ( fig.b) Step 1- Connect A and B on the two lines by a straight line. Step 2- With the center D on the perpendicular from A, draw the first are of known or chosen radius until it crosses the line AN at C. Step 3-Extend DC until it crosses the perpendicular from B at E. This locates the center for the second arc.

25

2.3.2 PROJECT (2) REGULAR POLYGON 2.3.2.1 Hexagon With 30/60 Triangle

Fig. (25) Constructing a hexagon with distance across flat given Draw a circle with the distance across flats as a diameter, and circumscribe a hexagon about the circle with a T-square and triangle.

2.3.2.2 Constructing A Regular Hexagon, Given The Distance Across Flats Given: The distance across flats, AB, in Fig (26). Step 1: Draw a horizontal center line through AB and a perpendicular bisector center line of AB called CD, whose center is O. Step 2: Placing the compass point at O, strike radius OA until it makes a complete circle. This should be a very light-weight line. Step 3: With a 30/60-degree triangle and a T-square, or by using a drafting machine, draw tangent lines as shown that establish the six sides of the hexagon (with opposite sides parallel and all sides equal in length. This construction practice is used in industry for drawing special hexagonal head bolts, screws, and nuts when templates are not available.

26

Fig. (26) Procedure for constructing a regular hexagon, given the distance across flats.

2.3.2.3 Hexagon With The Length Of Side Given

Fig. (27) Constructing a hexagon with length of side given

Step 1- Draw a circle with the length of a side as a radius. The diameter will be the distance across the corners. Step 2- The radius six times around the circle, and connect the point

27 2.3.2.4 Hexagon With The Distance Across Corners Given

Fig. (28) Constructing a hexagon with distance across corners given

Step 1- Draw a circle with the distance across the corners as a diameter, Step 2- The ends of the diameter as centers, draw two arcs as shown, thus locating six points including the ends of the diameter. Step 3- Connect the six points on the circle to form the hexagon.

2.3.2.5 Pentagon With The Inscribed In A Circle Of Given Radius .

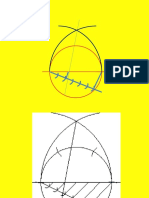
Fig. (29) Constructing a pentagon inscribed in a circle of given radius.

Step 1 - bisect radius CA. Step 2 -With center O and radius OB, draw are BD, With B as a center and radius BD, draw are DE, and step off this distance five times around the circle.

28 2.3.2.6 Subdivision Into 5 Parts

Fig. (30) Constructing a pentagon or subdivision into 5 parts. Step 1- Draw a diameter of the circle, and divide it into 5 equal parts. Step 2- With ends A and B as centers and a radius equal to the diameter of the circle, draw two arcs until they intersect. Step 3- From this point, C, draw a line through the second division point on the diameter, and continue it until it crosses the circle at D. The chord AD is one side of the polygon. Step 4- this distance the required number of times on the circle to locate the corners of the polygon 2.3.2.7 To Draw A Circle Of Radius R Tangent To Two Other Circle Tangent Externally

Fig. (31-a) Constructing of radius r tangent to two other circles Draw two arcs respectively concentric with the given circles and with radii equal to R+r and R1+r. The intersection of these arcs is the required center.

29

Tanget Internally

Fig. (31-b) In this case the radius of the tangent circle must be greater than that of either circle. Draw two arcs respectively concentric with the given circles with radii equal to r-R and r-R1. The intersection of these arcs is the required center. A practical application is shown in Fig.

30

2.3.3 PROJECT (3) ELLIPSE AND SPIRALS 2.3.3.1 Two Circles Or Projection Method

Fig. (32) Two circles or projection method Given : Major and minor axis Step 1- Draw two concentric circles whose diameters are equal respectively to the major and minor axes of the ellipse. Step 2- Divide each circle into 12 equal parts by drawing 30 and 60 radial lines, Step 3- From the point B where any radial line crosses the large circle, draw a line vertically down, and, from the point A where the same radial line cuts the small circle, drawn a line horizontally outward until the line intersects the vertical line previously drawn from B. The intersection C of these lines determines a point on the ellipse. . 2.3.3.2 Focal Distance Method

Fig. (33) Focal distance method Given : The foci F and F1 and the constant sum, AB, which is also the major axis of the ellipse. Step 1- Divide the space from F to the center into any convenient number of parts. Step 2- Set the compass to the distance A-1, and, with F and F1 as centers, descrube four arcs, Then set the compass to B-1, and with the same centers describe four arcs intersecting the first four. These intersections will lie on the ellipse. Repeat for the other points on the axis to determine as many points on the ellipse as desired. Step 3- Draw a smooth curve through these points.

31

2.3.3.3 Four Centres Method

Fig. (34) Four centers approximate method Step 1-Draw the enclosing rectangle and its enter lines as in fig. Step 2- Then draw the diagonal BC of one of the quarters of this rectangle. With center O draw an arc with radius OA cutting the minor axis at E. Step 3- With center at C and radius CE, draw an arc cutting the diagonal CN at F. Step 4- Construct the perpendicular bisector of FB, and extend the bisector until it cuts the center lines, this locating two of the four centers. The remaining two many be located by summetry.

2.3.3.4 Isometric Circle

Fig.(35) The four-center system for constructing the isometric circle.

Given : The basic forms of regular circle A, whose radius is r, and isometric circle B, both with horizontal and vertical center lines whose points are identified as 1,2,3 and 4 .

32

Step 1: Draw a horizontal center line. Construct a vertical isometric center line at a 60- degree angle with a triangle or a drafting machine. Using the given radius from the regular circle, strike radius r on the construction, making certain that the radius intercets the center lines at points 1,2,3,and 4. Step 2: Construct the basic isometric form. Draw four lines at 90 degrees, one from each tangent point, as shown . Note that these four lines intersect at two places. Identify these intersection at C and D. Step 3: Strike minor radii from points C and D and major radii from point E and F, using light weight lines. Each of the four radii equals one-fourth of the isometric circle.

2.3.3.5 Constant Pitch Spirals

Fig. (36) Constant pitch spirals The figure (a) shows a common construction, in which the centres are located at the corners of a square (side s) shown enlarged at (b). The curve then becomes the involute of the square, and is built ip of quadrantal circular arcs. Observe that the pitch is constant and equal to 4s, the perimeter of the square. 2.3.3.6 Ionic Volute Spirals

Fig. (37) Ionic volute spirals

33

In the first method (a), the centres of the arcs are at the corners of three squares, arranged as shown (see the enlarged view to the left). A circle, centre O, is first drawn, for the eye of the volute. The spiral is then built of the arcs, with centres 1,2,3,... as is sufficuently clear from the figure. If s1, s2, s3 stand for the sides of the squares, the various pitches are evidently those figured in the diagram. A more artistic curve, consisting of involutes of circles, would result if the squares were replaced by circles, touching one another at O.

2.3.4 PROJECT (4) PARABOLA AND HYPERBOLA 2.3.4.1 Parabola

.Fig. (38) Parabola Step 1- Divide the lines avcv and bvdv into the same number of equal parts, Step 2- number one toward the intersection and the other away from it. Connect points of the same number, and draw a smooth curve tangent to them. If the two tangents are equal, the curve is symmetrical about the bisector of the angle. If the two tangents are unequal, the curve is still a parabola but the portion joining the lines is an unsymmetrical part.

34

2.3.4.2 Hyperbola

Fig. (39) Hyperbola Divide the base circle into a number of equal parts in the plan view and draw the horizontal projection of the elements through these points tangent to the gorge circle. Project the ends of the elements to the elevation, and draw in the elements. Construction 2. Having given the axis OM and the generatrix AB, as in Fig 14.89, draw the gorge circle with a radius CN equal to the perpendicular distance from OM to AB. Project cV up to cH on aHbH, and through cH draw the vertical projection of the gorge circle perpendicular to the axis. Then locate the limiting points D and E on the gorge circle, the vertices of the horizontal projection this process is repeated and other points on the hyperbola obtained.

35

36 CHAPTER III MULTI-VIEW DRAWING 3.1PURPOSE The purpose of the multi-view drawing is to represent the various faces of an object in two or more views on planes at right angles to each other by extending perpendicular projection lines from the object to these planes. The multi-view drawing allows the observer to view an object from more than one orientation. Top view or plan- the object appears when viewed from above Front view or front elevation- the object appears when viewed from front Side view or side elevation- the object appears when viewed from side.

3.2 BASIC PRINCIPLES The basic principles identified below will assist the learner in the solution of problems in descriptive geometry. 1. In orthographic (third angle ) projection , The multiview drawing, the plane is always between the object and the observer, with the object and the observer, with the object changing position to accommodate the observer. In descriptive geometry, the observer changes position, not the object. 2. For the various views required, projection planes are always rotated into the plane of the drawing through a 90-degree angle. Rotation of the object takes place about lines which may be seen as hinged between adjacent projection planes. These lines which fold or rotate are called reference lines, as shown in Figure 13.1. Reference lines are to be used as temporary construction lines and should not appear on the finished drawing. 3. For separate observation of each view, reference lines represent edge views of other projection planes. 4. The lines of sight from the object to each projection plane are parallel with each other and perpendicular to the projection plane. 5. Perpendicular distances from the projection plane to the object are equal distances in all views perpendicular to that plane. Terminology Used In Descriptive Geometry There are several important terms related to descriptive geometry with which the learner should become familiar. These terms are defined below. Notation A systematic means of identifying points and views on a drawing. For example, the learner may wish to use the following guidelines in the solution of graphical problems.

37 Use lower-case letters (a, b, c, etc.) for all points. Use upper-case letters for all views. (Example: F=front view; T=top view; L=left side view; R=right side view; A=auxiliary view(s); B thru Z=all other views) Two or more points may be combined to locate a line. Upper- and lower-case letters may be combined to identify a point on a specific view. Plane Normally refers to a surface, such as a flat plane surface. It is the place, anywhere on a surface, where two points is surface, which is not curved or warped. True shape The true and actual shape of a surface. True length The true and actual length of a line. Edge view A view of a plane where in all lines of the plane appear to coincide in a single line. Line of sight An imaginary straight line from the eye of the observer to a point on the object being observed. Point view A view of a line wherein the line of sight is parallel with the line, resulting in a single point. Normal view A view of a plane wherein the line of sight is perpendicular to the plane.

Fig. (40) Pictorial illustration of basic principle of descriptive geometry

38 3.3 THIRD-ANGLE PROJECTION The predominant method for producing multi-view drawings is called third angle projection. In third angle orthographic projection, different views of an object (front, top, and side) are systematically arranged on a drawing medium to convey necessary information to the reader. Features are projected from one view to another.

Fig. (41) Transparent box encompassing object to be drawn

Fig. (42) (a) unfolding box (b) six view third angle projection

In the above figure (41), the object to be drawn placed inside the box so that its axes are parallel to the axes of the box. The projections on the sides of the box are the views one sees by looking straight at the object through each side. If each view is drawn as seen on the side of the box and the box is unfolded and laid flat as shown at the next figure (42-a, b), the result is a six-view orthographic projection, better known as a multi-view drawing. Any of the six-views could be regarded as the principal view, and the box could be folded out from one view as easily as from another. When the box is unfolded from the front view of the object, it is called third-angle projection.

39 3.3.1 The Selected And Placement Of Views The important view placement principles include: 1. The front and plan (top) views must always be aligned vertically, with the top view above the front view. 2. The front view and the side view(s) must always be aligned horizontally. The right side view must be drawn to the right of the front view, and the left side view must be drawn to the left of the front view. 3. The depth of the top view must always be the same as the depth of the side view(s). 4. The length of the top view must always be the same as the length of the front view. 5. The height of the side view(s) must always be the same as the height of the front view. 6. The bottom view must always be shown below and vertically aligned with the front view.

Fig. (43) Acceptable relationships between the depths of the top view and the side view(s)

3.4 DIMENSION 3.4.1The purpose of dimensions Dimensions on a drawing provide the producer of the object with the necessary information regarding the exact size and location of each feature of the part. A dimension is a numerical value expressed in appropriate units of measure. It is identified on a drawing, along with lines, symbols, and text, to define the geometrical characteristics of an object. Dimensions are used to complete the description of an object or a part. The ultimate user of the drawing must always be kept in mind when dimensions are being added to a drawing.

40 3.4.2 Fundamental Rules of Dimensioning For dimensions to define geometrical characteristics clearly and concisely, the drafter should follow a few basic rules in order to produce quality technical drawings. These rules will become obvious as one reads throughout this section. The rule include: Show enough dimensions so that the intended sizes and shapes can be determined without making calculations or assuming distances. State each dimension clearly, so that it can be interpreted in only one way. Dimension and extension lines shall not cross each other unless absolutely necessary. Whenever possible, dimension each feature in the view where it appears. Dimensioning to hidden lines should be avoided, when possible. Place dimensions outside the outline of the object.

3.4.3Type of Dimensioning Systems The dimensioning system most commonly used in architectural drafting is known as aligned dimensioning. With this system, dimensions are placed in line with the dimension lines and read from the bottom or right side of the sheet. Dimension numerals are centered on and placed above the solid dimension lines. 3.4.4Basic Dimensioning Concepts When placing dimensions, space dimension lines a minimum of 3/8 from the object and from each other. Extension and dimension lines are drawn thin and dark. They are drawn in this manner so they do not distract from the overall appearance and balance of the drawing. Dimension lines terminate at extension lines with dots, arrowheads, or slash marks that are each drawn in the same direction. The dimension units used are feet and inches for all lengths over 12. Inches and fractions are used for units less than 12. Foot units are followed by the symbol () and inch units are shown with the symbol (). 3.4.5 The Dimension Line The dimension line, with terminations called "arrowheads", shows the direction and extent of a dimension. Numerals indicate the number of units of a measurement. Preferably, dimension lines should be broken for insertion of numerals. When a horizontal dimension line is not broken, numerals are placed above and parallel to the dimension line. Dimension lines are aligned, if possible, and grouped for easier readability and uniform appearance. Dimension lines should always be drawn parallel to the direction of measurement. The space between the first dimension line and the object outline should not be less than .40 inch. The space between succeeding parallel dimension lines should not be less than .25 inch.

41

Fig. (44) Dimension lines.

Fig. (45) Grouping of dimension.

Fig. (46) Spacing of dimensions.

3.4.6 The Extension Line The extension line, which is also referred to as the projection line. There should be a visible gap between the object and an extension line.

Fig. (47) Extension lines.

Fig. (48) Breaks in extension lines.

1.5 STUDENTS PROJECT (a) Simple form (b) Building form