Académique Documents
Professionnel Documents
Culture Documents
Problem
Transféré par
Leonora Erika RiveraDescription originale:
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Problem
Transféré par
Leonora Erika RiveraDroits d'auteur :
Formats disponibles
Problem In a study of the television viewing habits of children, a developmental psychologist selects a random sample of 300 first graders
- 100 boys and 200 girls. Each child is asked which of the following TV programs they like best: The Lone Ranger, Sesame Street, or The Simpsons. Results are shown in the contingency table below. Viewing Preferences Row total Lone Ranger Sesame Street The Simpsons 50 30 20 100 Boys 50 80 70 200 Girls 100 110 90 300 Column total Do the boys' preferences for these TV programs differ significantly from the girls' preferences? Use a 0.05 level of significance. Solution The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below: State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis. o Null hypothesis: The null hypothesis states that the proportion of boys who prefer the Lone Ranger is identical to the proportion of girls. Similarly, for the other programs. Thus, H0: Pboys who prefer Lone Ranger = Pgirls who prefer Lone Ranger H0: Pboys who prefer Sesame Street = Pgirls who prefer Sesame Street H0: Pboys who prefer The Simpsons = Pgirls who prefer The Simpsons o o Alternative hypothesis: At least one of the null hypothesis statements is false. Formulate an analysis plan. For this analysis, the significance level is 0.05. Using sample data, we will conduct a chisquare test for homogeneity. Analyze sample data. Applying the chi-square test for homogeneity to sample data, we compute the degrees of freedom, the expected frequency counts, and the chi-square test statistic. Based on the chi-square statistic and the degrees of freedom, we determine the P-value. DF = (r - 1) * (c - 1) = (2 - 1) * (3 - 1) = 2 Er,c = (nr * nc) / n E1,1 = (100 * 100) / 300 = 10000/300 = 33.3 E1,2 = (100 * 110) / 300 = 11000/300 = 36.7 E1,3 = (100 * 90) / 300 = 9000/300 = 30.0 E2,1 = (200 * 100) / 300 = 20000/300 = 66.7 E2,2 = (200 * 110) / 300 = 22000/300 = 73.3 E2,3 = (200 * 90) / 300 = 18000/300 = 60.0 2 = [ (Or,c - Er,c)2 / Er,c ] = (50 - 33.3)2/33.3 + (30 - 36.7)2/36.7 + (20 - 30)2/30 + (50 - 66.7)2/66.7 + (80 - 73.3)2/73.3 + (70 - 60)2/60 2 2 = (16.7) /33.3 + (-6.7)2/36.7 + (-10.0)2/30 + (-16.7)2/66.7 + (3.3)2/73.3 + (10)2/60 2 = 8.38 + 1.22 + 3.33 + 4.18 + 0.61 + 1.67 = 19.39 where DF is the degrees of freedom, r is the number of populations, c is the number of levels of the categorical variable, n r is the number of observations from population r, nc is the number of observations from level c of the categorical variable, n is the number of observations in the sample, Er,c is the expected frequency count in population r for level c, and Or,c is the observed frequency count in population r for level c. The P-value is the probability that a chi-square statistic having 2 degrees of freedom is more extreme than 19.39. We use the Chi-Square Distribution Calculator to find P(2 > 19.39) = 0.0000. (The actual P-value, of course, is not exactly zero. If the Chi-Square Distribution Calculator reported more than four decimal places, we would find that the actual P-value is a very small number that is less than 0.00005 and greater than zero.) Interpret results. Since the P-value (0.0000) is less than the significance level (0.05), we reject the null hypothesis. Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, each population was more than 10 times larger than its respective sample, the variable under study was categorical, and the expected frequency count was at least 5 in each population at each level of the categorical variable.
2
Vous aimerez peut-être aussi
- Business Statistics Module - 1 Introduction-Meaning, Definition, Functions, Objectives and Importance of StatisticsDocument5 pagesBusiness Statistics Module - 1 Introduction-Meaning, Definition, Functions, Objectives and Importance of StatisticsPnx RagePas encore d'évaluation
- Laerd Statistics 2013Document3 pagesLaerd Statistics 2013Rene John Bulalaque Escal100% (1)
- Central TendencyDocument26 pagesCentral Tendencyবিজয় সিকদারPas encore d'évaluation
- 1 Nature of StatisticsDocument7 pages1 Nature of StatisticsJay SerdonPas encore d'évaluation
- 7 Chi-Square Test For IndependenceDocument3 pages7 Chi-Square Test For IndependenceMarven LaudePas encore d'évaluation
- Measure of Central TendencyDocument13 pagesMeasure of Central TendencyNawazish KhanPas encore d'évaluation
- Presentation 3Document37 pagesPresentation 3Swaroop Ranjan Baghar100% (1)
- Sample Mid-Term Exam (The Sample Contains Only 20 Questions)Document5 pagesSample Mid-Term Exam (The Sample Contains Only 20 Questions)Phan Huỳnh Châu TrânPas encore d'évaluation
- Z-Test FormulaDocument24 pagesZ-Test FormulaSalem Quiachon III100% (2)
- Sampling Distributions, Estimation and Hypothesis Testing - Multiple Choice QuestionsDocument6 pagesSampling Distributions, Estimation and Hypothesis Testing - Multiple Choice Questionsfafa salah100% (1)
- Chapter Three Hypothesis TestingDocument16 pagesChapter Three Hypothesis Testingtemedebere100% (1)
- Phase 1 & 2: 50% OFF On NABARD Courses Code: NABARD50Document23 pagesPhase 1 & 2: 50% OFF On NABARD Courses Code: NABARD50SaumyaPas encore d'évaluation
- Exam History of Economic ThoughtDocument3 pagesExam History of Economic ThoughtLeonardo VidaPas encore d'évaluation
- Unit 1: Measures of Central Tendency: Module 6: Descriptive Statistical MeasuresDocument10 pagesUnit 1: Measures of Central Tendency: Module 6: Descriptive Statistical MeasuresABAGAEL CACHOPas encore d'évaluation
- Sample Final Exam 1Document13 pagesSample Final Exam 1upload55Pas encore d'évaluation
- Chapter Two: Statistical Estimation: Definition of Terms: Interval EstimateDocument15 pagesChapter Two: Statistical Estimation: Definition of Terms: Interval EstimatetemedeberePas encore d'évaluation
- Course Introduction Inferential Statistics Prof. Sandy A. LerioDocument46 pagesCourse Introduction Inferential Statistics Prof. Sandy A. LerioKnotsNautischeMeilenproStundePas encore d'évaluation
- Chi Square Test: Testing Several Proportions Goodness-of-Fit Test Test of IndependenceDocument3 pagesChi Square Test: Testing Several Proportions Goodness-of-Fit Test Test of IndependenceJustin ZunigaPas encore d'évaluation
- Managerial Statistics UuDocument138 pagesManagerial Statistics UuSolomonPas encore d'évaluation
- Uses of Index NumbersDocument7 pagesUses of Index NumbersAjay KarthikPas encore d'évaluation
- Sampling Distribution EstimationDocument21 pagesSampling Distribution Estimationsoumya dasPas encore d'évaluation
- Sampling Distribution Revised For IBS 2020 BatchDocument48 pagesSampling Distribution Revised For IBS 2020 Batchnandini swamiPas encore d'évaluation
- Chi Square DistributionDocument4 pagesChi Square DistributionIziPas encore d'évaluation
- Module 2 - Research MethodologyDocument18 pagesModule 2 - Research MethodologyPRATHAM MOTWANI100% (1)
- T-Test Z TestDocument33 pagesT-Test Z TestJovenil BacatanPas encore d'évaluation
- Chow TestDocument23 pagesChow TestYaronBabaPas encore d'évaluation
- CHAPTER TWO-Econometrics I (Econ 2061) Edited1 PDFDocument35 pagesCHAPTER TWO-Econometrics I (Econ 2061) Edited1 PDFanwar muhammedPas encore d'évaluation
- What Are The Components of A Compensation SystemDocument5 pagesWhat Are The Components of A Compensation SystemLing Ching YapPas encore d'évaluation
- 4 Confidence IntervalsDocument49 pages4 Confidence Intervalsasvanth100% (1)
- Measure of Central TendencyDocument113 pagesMeasure of Central TendencyRajdeep DasPas encore d'évaluation
- Common Course From Chapter One To FiveDocument120 pagesCommon Course From Chapter One To Fiveገብረዮውሃንስ ሃይለኪሮስ67% (3)
- LECTURED Statistics RefresherDocument123 pagesLECTURED Statistics RefreshertemedeberePas encore d'évaluation
- Statistics: Class Mark Cumulative Frequency Histogram Frequency Polygon Mean Median ModeDocument27 pagesStatistics: Class Mark Cumulative Frequency Histogram Frequency Polygon Mean Median ModeyugiPas encore d'évaluation
- CH 3 and 4Document44 pagesCH 3 and 4zeyin mohammed aumer100% (4)
- CH 3 Statistical EstimationDocument13 pagesCH 3 Statistical EstimationManchilot Tilahun100% (1)
- Lesson 12 T Test Dependent SamplesDocument26 pagesLesson 12 T Test Dependent SamplesNicole Daphnie LisPas encore d'évaluation
- Mathematical Formulation of Linear Programming ProblemsDocument5 pagesMathematical Formulation of Linear Programming ProblemsAnandKuttiyanPas encore d'évaluation
- Simple Linear RegressionDocument24 pagesSimple Linear Regressionইশতিয়াক হোসেন সিদ্দিকীPas encore d'évaluation
- Classical Theories of Economic Growth and DevelopmentDocument65 pagesClassical Theories of Economic Growth and DevelopmentstudentPas encore d'évaluation
- Render 10Document28 pagesRender 10eliane вelénPas encore d'évaluation
- Correlation CoefficientDocument3 pagesCorrelation CoefficientbalubalubaluPas encore d'évaluation
- Probability DistributionsDocument17 pagesProbability Distributionstamann2004Pas encore d'évaluation
- Test of Goodness of FitDocument3 pagesTest of Goodness of FitSunil KumarPas encore d'évaluation
- Operation ResearchDocument7 pagesOperation ResearchSohail AkhterPas encore d'évaluation
- Measures of Central TendencyDocument35 pagesMeasures of Central TendencyRenukadevi NavaneethanPas encore d'évaluation
- Chapter 3 Data DescriptionDocument140 pagesChapter 3 Data DescriptionNg Ngọc Phương NgânPas encore d'évaluation
- Buss. Stat CH-2Document13 pagesBuss. Stat CH-2Jk K100% (1)
- Review Questions For FinalDocument29 pagesReview Questions For FinalTran Pham Quoc Thuy100% (2)
- Post Optimality AnalysisDocument13 pagesPost Optimality AnalysislitrakhanPas encore d'évaluation
- Statistical Analysis: Session 2: Measures of Central TendencyDocument41 pagesStatistical Analysis: Session 2: Measures of Central Tendencypriyankamodak100% (1)
- 7 Normal DistributionDocument35 pages7 Normal DistributionMayie Baltero100% (1)
- 4 Circuit TheoremsDocument40 pages4 Circuit TheoremsTanmoy PandeyPas encore d'évaluation
- Chapter 18 Nonparametric Methods AnalysiDocument17 pagesChapter 18 Nonparametric Methods Analysiyoussef888 tharwatPas encore d'évaluation
- Mean Is Meaningless: Guide For Interpretinng Likert ScaleDocument3 pagesMean Is Meaningless: Guide For Interpretinng Likert ScaleRJ Bedaño100% (1)
- Karl Pearson's Measure of SkewnessDocument27 pagesKarl Pearson's Measure of SkewnessdipanajnPas encore d'évaluation
- Chapter 1&2Document27 pagesChapter 1&2SamiMasreshaPas encore d'évaluation
- Graphical Representation of DataDocument36 pagesGraphical Representation of DataNihal AhmadPas encore d'évaluation
- Statistics - Chi Square: Test of Homogeneity (Reporting)Document21 pagesStatistics - Chi Square: Test of Homogeneity (Reporting)Ionacer Viper0% (1)
- ACCT3563 Issues in Financial Reporting Analysis Part A S12013 1Document3 pagesACCT3563 Issues in Financial Reporting Analysis Part A S12013 1Yousuf khanPas encore d'évaluation
- Chi Square TestDocument11 pagesChi Square Testmellite copperPas encore d'évaluation
- Student Teaching Experiences IN Bicol University College of Education Integrated Laboratory School Daraga, AlbayDocument2 pagesStudent Teaching Experiences IN Bicol University College of Education Integrated Laboratory School Daraga, AlbayLeonora Erika RiveraPas encore d'évaluation
- Survey-Questionnaire (Household Head)Document3 pagesSurvey-Questionnaire (Household Head)Leonora Erika RiveraPas encore d'évaluation
- Hyperbola With Center at (H, K)Document3 pagesHyperbola With Center at (H, K)Leonora Erika RiveraPas encore d'évaluation
- Pie Charts: December 3, 2015 Typesofgraphs01Document5 pagesPie Charts: December 3, 2015 Typesofgraphs01Leonora Erika RiveraPas encore d'évaluation
- Calculus Written ReportDocument4 pagesCalculus Written ReportLeonora Erika RiveraPas encore d'évaluation
- Leonora Erika O. Rivera: Career ObjectiveDocument1 pageLeonora Erika O. Rivera: Career ObjectiveLeonora Erika RiveraPas encore d'évaluation
- Objective: Work ExperiencedDocument2 pagesObjective: Work ExperiencedLeonora Erika RiveraPas encore d'évaluation
- Progress ChartDocument2 pagesProgress ChartLeonora Erika RiveraPas encore d'évaluation
- Statistic: Price IndexDocument3 pagesStatistic: Price IndexLeonora Erika RiveraPas encore d'évaluation
- Chapter III (Thesis)Document7 pagesChapter III (Thesis)Leonora Erika RiveraPas encore d'évaluation
- January 15Document1 pageJanuary 15Leonora Erika RiveraPas encore d'évaluation
- Prof - Ed14 Chapter One (Thesis)Document11 pagesProf - Ed14 Chapter One (Thesis)Leonora Erika RiveraPas encore d'évaluation
- SurveyDocument3 pagesSurveyLeonora Erika RiveraPas encore d'évaluation
- Transcript of Copy of Yearbook Proposal Middle School 2013Document3 pagesTranscript of Copy of Yearbook Proposal Middle School 2013Leonora Erika RiveraPas encore d'évaluation
- Lesson Plan in English ViDocument3 pagesLesson Plan in English ViLeonora Erika RiveraPas encore d'évaluation
- Chemistry Third Quarter ExaminationDocument3 pagesChemistry Third Quarter ExaminationLeonora Erika Rivera100% (2)
- Masbate CollegesDocument9 pagesMasbate CollegesLeonora Erika RiveraPas encore d'évaluation
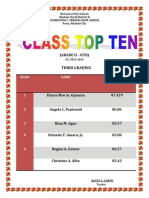
- (Grade Ii - Atis) : Third GradingDocument1 page(Grade Ii - Atis) : Third GradingLeonora Erika RiveraPas encore d'évaluation
- Masbate CollegesDocument9 pagesMasbate CollegesLeonora Erika RiveraPas encore d'évaluation
- DEPEDDocument2 pagesDEPEDLeonora Erika RiveraPas encore d'évaluation
- The Eight Beatitudes of JesusDocument4 pagesThe Eight Beatitudes of JesusLeonora Erika RiveraPas encore d'évaluation
- Lesson Plan in Mathematics IIDocument3 pagesLesson Plan in Mathematics IILeonora Erika Rivera80% (35)
- Correlation Regression Hypo ANOVADocument22 pagesCorrelation Regression Hypo ANOVAluis anchayhua pradoPas encore d'évaluation
- UECM1693/UECM2623/UCCM2623 Tutorial S4: Applications of Statis-TicsDocument2 pagesUECM1693/UECM2623/UCCM2623 Tutorial S4: Applications of Statis-Ticssadyehclen0% (1)
- FmerneetDocument54 pagesFmerneetcharibhargav04Pas encore d'évaluation
- Results Calculator PDFDocument6 pagesResults Calculator PDFSilvia GarcíaPas encore d'évaluation
- Gmat - Graduate Management Admission Test Official Score Report - Test TakerDocument3 pagesGmat - Graduate Management Admission Test Official Score Report - Test TakerAnonymous uc6yv6Pas encore d'évaluation
- JSREP - Volume 34 - Issue 165 - Pages 457-482Document26 pagesJSREP - Volume 34 - Issue 165 - Pages 457-482صالح الشبحيPas encore d'évaluation
- 1 Statistics and Probability g11 Quarter 4 Module 1 Test of HypothesisDocument36 pages1 Statistics and Probability g11 Quarter 4 Module 1 Test of HypothesisISKA COMMISSIONPas encore d'évaluation
- Graph: Item Analysis With MPS, Frequency of Errors and Mastery LevelDocument1 pageGraph: Item Analysis With MPS, Frequency of Errors and Mastery LevelEsphie Arriesgado100% (1)
- Jatin Aghara - 406141592 - ESRDocument10 pagesJatin Aghara - 406141592 - ESRHarsh GuptaPas encore d'évaluation
- Sign TestDocument17 pagesSign TestAlex LovesmangoesPas encore d'évaluation
- Gate Iitd Ac in EEKey PHPDocument2 pagesGate Iitd Ac in EEKey PHPshagun gargPas encore d'évaluation
- Comparing Group Means: The T-Test and One-Way ANOVA Using STATA, SAS, and SPSSDocument179 pagesComparing Group Means: The T-Test and One-Way ANOVA Using STATA, SAS, and SPSSwulandari_rPas encore d'évaluation
- Statistical Hypothesis:: Details At:::::::::::::::::::::http://goo - gl/7DztnDocument11 pagesStatistical Hypothesis:: Details At:::::::::::::::::::::http://goo - gl/7DztnJasper ShaonPas encore d'évaluation
- 1 Tail & 2 Tail TestDocument3 pages1 Tail & 2 Tail TestNisha AggarwalPas encore d'évaluation
- Anova: Two-Factor With ReplicationDocument3 pagesAnova: Two-Factor With Replicationracnal ulinnuhaPas encore d'évaluation
- 9231974 (1)Document1 page9231974 (1)Surendra MurmuPas encore d'évaluation
- Manual Testing SyllabusDocument4 pagesManual Testing SyllabusBaranishankarPas encore d'évaluation
- Dangote Fertilizer Project NDT Analysis For U/G: Radiographic Test - Ultrasonic TestDocument6 pagesDangote Fertilizer Project NDT Analysis For U/G: Radiographic Test - Ultrasonic Testaakash100% (1)
- Power of TestDocument3 pagesPower of TestEmy AL-AnaziPas encore d'évaluation
- GPower ProtocolDocument4 pagesGPower Protocolmb861972Pas encore d'évaluation
- ANOVA IntroductionDocument14 pagesANOVA Introductionlavaniyan100% (3)
- CH 3Document14 pagesCH 3Wudneh AmarePas encore d'évaluation
- General Reading Answer Sheet PDFDocument1 pageGeneral Reading Answer Sheet PDFMavi Tv LivePas encore d'évaluation
- Common Entrance ExamDocument2 pagesCommon Entrance ExamdheerajPas encore d'évaluation
- NTA JEE 2024 - 27 29 30 31 Jan 1st Feb 2024Document42 pagesNTA JEE 2024 - 27 29 30 31 Jan 1st Feb 2024fkkpaceonlineopPas encore d'évaluation
- Chapter 5 - Sanity Testing Vs Smoke TestingDocument4 pagesChapter 5 - Sanity Testing Vs Smoke TestingAamir AfzalPas encore d'évaluation
- Quantitative Ability Reasoning Ability Verbal Ability: Que Ans Que Ans Que Ans Que Ans Que Ans QueDocument2 pagesQuantitative Ability Reasoning Ability Verbal Ability: Que Ans Que Ans Que Ans Que Ans Que Ans QueHemanth JPas encore d'évaluation
- Why Do I Do What I DoDocument23 pagesWhy Do I Do What I DoRakesh Kumar MundaPas encore d'évaluation
- Response SheetDocument39 pagesResponse SheetKritika PuriPas encore d'évaluation
- A Primer On Strong Vs Weak Control of Familywise Error Rate: Michael A. Proschan Erica H. BrittainDocument7 pagesA Primer On Strong Vs Weak Control of Familywise Error Rate: Michael A. Proschan Erica H. BrittainjaczekPas encore d'évaluation
- Mental Math: How to Develop a Mind for Numbers, Rapid Calculations and Creative Math Tricks (Including Special Speed Math for SAT, GMAT and GRE Students)D'EverandMental Math: How to Develop a Mind for Numbers, Rapid Calculations and Creative Math Tricks (Including Special Speed Math for SAT, GMAT and GRE Students)Pas encore d'évaluation
- Quantum Physics: A Beginners Guide to How Quantum Physics Affects Everything around UsD'EverandQuantum Physics: A Beginners Guide to How Quantum Physics Affects Everything around UsÉvaluation : 4.5 sur 5 étoiles4.5/5 (3)
- Limitless Mind: Learn, Lead, and Live Without BarriersD'EverandLimitless Mind: Learn, Lead, and Live Without BarriersÉvaluation : 4 sur 5 étoiles4/5 (6)
- Build a Mathematical Mind - Even If You Think You Can't Have One: Become a Pattern Detective. Boost Your Critical and Logical Thinking Skills.D'EverandBuild a Mathematical Mind - Even If You Think You Can't Have One: Become a Pattern Detective. Boost Your Critical and Logical Thinking Skills.Évaluation : 5 sur 5 étoiles5/5 (1)
- Basic Math & Pre-Algebra Workbook For Dummies with Online PracticeD'EverandBasic Math & Pre-Algebra Workbook For Dummies with Online PracticeÉvaluation : 4 sur 5 étoiles4/5 (2)
- Math Workshop, Grade K: A Framework for Guided Math and Independent PracticeD'EverandMath Workshop, Grade K: A Framework for Guided Math and Independent PracticeÉvaluation : 5 sur 5 étoiles5/5 (1)
- Images of Mathematics Viewed Through Number, Algebra, and GeometryD'EverandImages of Mathematics Viewed Through Number, Algebra, and GeometryPas encore d'évaluation
- Fluent in 3 Months: How Anyone at Any Age Can Learn to Speak Any Language from Anywhere in the WorldD'EverandFluent in 3 Months: How Anyone at Any Age Can Learn to Speak Any Language from Anywhere in the WorldÉvaluation : 3 sur 5 étoiles3/5 (80)
- ParaPro Assessment Preparation 2023-2024: Study Guide with 300 Practice Questions and Answers for the ETS Praxis Test (Paraprofessional Exam Prep)D'EverandParaPro Assessment Preparation 2023-2024: Study Guide with 300 Practice Questions and Answers for the ETS Praxis Test (Paraprofessional Exam Prep)Pas encore d'évaluation
- A Mathematician's Lament: How School Cheats Us Out of Our Most Fascinating and Imaginative Art FormD'EverandA Mathematician's Lament: How School Cheats Us Out of Our Most Fascinating and Imaginative Art FormÉvaluation : 5 sur 5 étoiles5/5 (5)
- Interactive Math Notebook: Geometry WorkbookD'EverandInteractive Math Notebook: Geometry WorkbookÉvaluation : 5 sur 5 étoiles5/5 (5)