Acta Mechanica 21, 173--192 (1975)

| by Springer-Verlag 1975
A Model of Nonlinearly Hardening Materials
for Complex Loading
By
Y. F. Da~alias and E. P. Popov, Berkeley, California
With 10 Figures
(Received January 2, 197d)
Summar y- Zusammenfassung
A Model of Nonlinearl F Hardening Materials for Complex Loadings. A number of
observations are made on the macroscopic behavior of materials subjected to uniaxial random
cyclic loadings. These observations are then generalized to construct a model describing the
material behavior for complex multiaxial loadings, in particular for cyclic loadings. This
generalization introduces the concept of a bounding surface in the stress space which always
encloses the loading surface. A parameter defined by the relative position of the loading
and the bounding surface, and the plastic work done during the most recent loading, de-
termine the value of the plastic modulus.
Ein )i odel l flit Werkstoffe mit niehflinearer Ver~estigung unter zusammengesetzter
Belastung. Zahlreiche Beobachtungen des makroskopischen Verhaltens yon Werkstoffen
unter beliebiger zyklischer einachsiger Belastung werden gemacht. Diese Beobachtungen
werden dann verallgemeinert, um ein Mode]l des Werkstoffverhaltens ffir zusammengesetzte,
insbesondere zyklische Belastung zu entwickeln. Diese Verallgemeinerung ffihrt zum Konzept
der die Belastungsfli~che ste~s einhfillenden Grenzfl~che im Spannungsraum. Ein durch die
relative Lage der Belastungsfl~iche zur Grenzfl~che definierter Parameter und die plastische
Arbeit w~hrcnd der letzten Belastung bestimmen den Weft des Plastizit~tsmoduls.
1. I n~oduef i on
I t is becoming increasingly i mport ant to describe the material behavior in the
plastic range as accurately as possible. The needed refinements of the existing
theories are mot i vat ed by the practical necessity of achieving a better agreement
with the experimental results for complex loading histories, such as occur under
cyclic loading. For simple histories, the widely used models of isotropic or kine-
matic hardening materials are reasonably good, and are simple enough to allow
analytical solutions of some boundary values problems. On the other hand, for
complex loading histories in the plastic range, the constitutive relations must
include a more realistic dependence on the loading history. The basic step in
considering this history dependence, is the formulation of constitutive laws in
differential or incremental form. The material response for a given loading or
deformation is t hen obtained by integrating the incremental relations. Wi t h
conventional models, although the incremental form of the constitutive relations
Act a 5l ech. XXI / 3 i 3
174 Y. F. DAFALIAS and E. P. Pol'ov:
is used, t he har deni ng or soft eni ng mat er i al propert i es are not adequat el y de-
scribed. As a consequence, not onl y are diserepencies obser ved bet ween t he t heo-
ret i cal predi ct i ons and t he exper i ment al results, but t he models used are i ncapabl e
of describing even qual i t at i vel y some of t he obser ved phenomena: for exampl e,
damage accumul at i on due t o cyclic creep and cyclic soft eni ng, or st abi l i zat i on of
hyst eresi s loops af t er a cer t ai n number of cycles of loading. Thi s necessi t at es t he
devel opment of a more accur at e model for represent i ng t he mat er i al behavi or.
The use of mat hemat i cal l y compl ex models for compl ex l oadi ng processes
t ends t o make t he anal yt i cal solutions ext r emel y difficult, if not impossible.
However , wi t h t he use of advanced numeri cal met hods and comput ers, some of t he
pr act i cal difficulties can be overcome, and t he devel opment of refi ned models is
j ust i fi ed. Of course t he maxi mum possible si mpl i ci t y i n t he f or mul at i on of t he
appr opr i at e rules or laws of pl ast i ci t y remai ns essential.
Any model describing pl ast i c behavi or shoul d cont ai n t wo basic feat ures. One
of t hese is t he flow rul e, whi ch is an i ncr ement al pl ast i c st ress-st rai n rel at i on. I t is
const r uct ed wi t h t he assumpt i on of r at e i ndependence and t he exi st ence of a
pl ast i c pot ent i al whi ch usual l y coincides wi t h t he yi el d or l oadi ng surface. The
second essential f eat ur e is t he har deni ng rul e, whi ch defines t he change of t he
l oadi ng surface duri ng t he course of pl ast i c flow as well as t he change of t he
har deni ng (softening) pr oper t i es of t he mat eri al . Thi s par amet er is usual l y
expressed i n germs of t he pl ast i c modul us ent er i ng t he flow rul e. The par t of t he
har deni ng rul e concerned wi t h t he change of t he plastic modulus, is t he mai n
subj ect of this paper.
2. I I i s t ori eal Re ma r k s
I n t he l ast t went y year s ma ny models have been pr oposed t o define t he
changes whi ch ma y t ake place in t he l oadi ng surface. Some comment s on t he most
i mpor t ant ones of t hese follows. HIrLL and I-IoDGE [1], [2] pr oposed t he so-called
i sot ropi e har deni ng rule, accordi ng t o whi ch t he yi el d surface expands uni forml y.
Thi s model cont radi ct s t he Bauschi nger effect. To overcome t hi s di ffi cul t y,
ISHLI~SKI [3] and PgAG~R [4] i nt r oduced t he idea t hat t he yi el d surface t r ansl at es
wi t hout r ot at i on in t he stress space in t he di rect i on of t he st r ai n i ncrement . Thi s
model, known as t he ki nemat i c har deni ng model, was i mpr oved upon by ZI~C~LER
and SmELD [5], and ZI EGL~ [6]. A comprehensi ve pr esent at i on of several models
was also pr esent ed ver y ear l y by EDELMA~ and Dg u c ~ g [7]. A mor e compl ex
work-hardeni ng model i nt roduci ng def or mat i on and r ot at i on of t he initial yi el d
surface was discussed by B~TOV and SAwcz~: [8]. I n a series of papers, t he
concept of a f ami l y of l oadi ng surfaces t ha t are di st i nct f r om and enclose t he
yi el d surface was devel oped for ar bi t r ar y har deni ng rules and appl i ed for i sot ropi e
har deni ng by PgILLreS and SI ~ga~ows~I [9], JtrsT~zsso~ and PmLLres [10],
and E I s ~ N~ G and PHrLLIrS [11].
I n t he above models, emphasis is pl aced on how t o describe t he change of t he
yi el d-l oadi ng surfaces, and l i t t l e has been done as t o how t he wor k- har deni ng
pl ast i c modul i change. To cl ari fy this, KADASgEWCI~ and Novoz~ILOV [12]
pr oposed a f unct i on / for ki nemat i c har deni ng of t he f or m [ [ a ~ - - C(e)~) e)~] ~ Ko,
where a~r~ is t he stress, e~z is t he plastic st rai n, and K 0 is a const ant . The t er m C,
A Model of Nonlinearly Hardening Materials 175
a f unct i on of pl ast i c st rai n, appear s as t he wor khar deni ng pl ast i c modul us in t he
fl ow rule. EISE~BE~G and PmLLIPS [13] demons t r at ed t ha t t hi s rul e cannot
r epr esent a real i st i c mat er i al behavi or , because of t he f unct i onal dependence of C
on e~z. The y suggest ed a modi f i ed f or m /[CrKZ- C( K 0 S~KZ] = Ko, where
fi21 /~p zp u/2 wi t h t he dot s over t he quant i t i es havi ng t he usual meani ng of
der i vat i ves wi t h r espect t o t i me. Appl yi ng t hi s model t o a uni axi al r ever se l oadi ng,
t hey obt ai ned a mor e accept abl e descr i pt i on of t he mat er i al behavi or . However ,
in t hei r pr ocedur e, t he same val ue of t he pl ast i c t angent modul us is pr edi ct ed at
t he t er mi nat i on of pl ast i c l oadi ng in one sense as at t he i ni t i at i on of pl ast i c
rel oadi ng in t he opposi t e di rect i on. Thi s descr i pt i on of t he mat er i al behavi or is
not ent i r el y sat i sf act or y, and i t cannot pr edi ct cyclic phe nome na in a r eason-
abl e way.
I n devel opi ng a ve r y gener al t heor y f or an El ast i c- Pl ast i c Cont i nuum,
Gg E ~ and Na a g Di [14] obt ai ned a basi c r el at i on f or t he i sot her mal process
~I SM~V, where 2 is a scalar, SM2V is a appr opr i at e st ress t ens or
and bK~ is a second or der t ens or wi t h all quant i t i es as well a s / , bei ng f unct i ons
of t he s t at e vari abl es. Thi s i ndeed is a f or m of a const i t ut i ve r el at i on whi ch is
gener al enough f or descri bi ng t he phenomena under discussion. However , no
specific f or m of a model f or i mmedi at e numer i cal appl i cat i ons is suggest ed.
By empl oyi ng a di f f er ent appr oach some aut hor s used t he concept of a f ami l y
of surfaces in t he st ress space in or der t o descri be nonl i near har deni ng behavi or .
KoI ~E~ [15] showed t h a t t he slip t he or y of BATDFORD and BUDIANSKY [16] coul d
be vi sual i zed in t e r ms of a col l ect i on of yi el d surfaces in such a st ress space. Thi s
was not ext ended t o i ncor por at e t he concept of ki nemat i c har deni ng as a means
of obt ai ni ng a mor e r easonabl e r epr es ent at i on of t he nonl i near behavi or . Al t er -
nat i vel y, IwAN [i 7], s t ar t i ng f r om a one di mensi onal model , general i zed i t f or
mul t i - di mensi onal cases in t he st ress space b y assumi ng a col l ect i on of yi el d
surfaces i nst ead of t he usual single surface. Each one of t he yi el d surfaces obeys
a l i near wor k- har deni ng l aw of t he Pr ager t ype [4], but t he combi ned effect gi ves
ri se t o a nonl i near har deni ng law. The di st r i but i on of t hese surfaces i n t he st r ess
space can be cont i nuous or pi ecewi se const ant . I ndependent l y, in t wo paper s,
Mgoz [18], [19] pr opos ed a si mi l ar model i nt r oduci ng t he concept of a field of
wor k- har deni ng modul i . Thi s fi el d is def i ned b y a conf i gur at i on of surfaces of
cons t ant wor k- har deni ng modul i in t he st r ess space. He al so pr opos ed a new r ul e
of ki nemat i c har deni ng whi ch is di f f er ent f r om t hose of PI~AGEg, Hol)o]~ a nd
ZIEGLER. However , because of t he resul t s obt ai ned in some r ecent exper i ment s b y
Pnl~LrPs and TANG [20], t he adequacy of t he di f f er ent ki nemat i c har deni ng rul es
per haps shoul d be reconsi dered.
I n t hi s pa pe r a nonl i near wor k- har deni ng model of mat er i al behavi or is
pr opos ed whi ch is sui t abl e f or compl ex l oadi ng pat hs i ncl udi ng cyclic l oadi ng. The
basi c pur pos e of t he pr opos ed model is si mi l ar t o t ha t of t he paper s r evi ewed above,
especi al l y t hose of I WaN and MRoz, but t he concept ual s t r uct ur e under l yi ng t he
model is bel i eved t o be novel and appear s t o offer some f eat ur es of si mpl i ci t y. The
changes in t he pl ast i c modul us in t he course of pl ast i c def or mat i on are di r ect l y
r el at ed t o t he obs er ved cyclic phenomena. For t hi s r eason t he mai n f eat ur e of t he
model is t he descr i pt i on of t he ma nne r in whi ch t he pl ast i c modul us changes in
13"
176 Y. F. I)AI~ALIAS and E. P. t)oPov:
mul t i - di mensi onal st ress space, b y general i zi ng concl usi ons der i ved on a qual i -
t at i ve basi s f r om uni axi al l oadi ng exper i ment s. For a quant i t at i ve descr i pt i on
mor e exper i ment al i nf or mat i on is needed of a ki nd not avai l abl e at t hi s t i me.
3. General Observations for Uni axi al Loadi ng
The anal yt i cal descr i pt i on of t he st r ess- st r ai n cur ve for t he uni axi al l oadi ng of
a duct i l e mat er i al i nt o t he pl ast i c range, has been ext ensi vel y st udi ed f or compl ex
l oadi ng histories. Ver y good resul t s were achi eved in t he f or m of anal yt i cal
expressi ons of var i ous t ypes, r angi ng f r om a si mpl e bi l i near descr i pt i on t o mor e
sophi st i cat ed ones abl e t o descri be t he non- l i near pa r t of t he st r ess- st r ai n cur ve
wi t h good accur acy. However , i t was not possi bl e t o general i ze mos t of t hese
descri pt i ons f or t he uni axi al case in or der t o descri be t he cor r espondi ng pheno-
mena i n a hi gher di mensi on st ress space. One of t he except i ons is Pr ager ' s ki ne-
mat i c har deni ng rul e wi t h a const ant pl ast i c modul us, whi ch cor r esponds t o t he
bi l i near descr i pt i on in t he uni axi al ease.
I n t hi s sect i on t he uni axi al ease is st udi ed in detail. The pur pos e of t hi s s t udy is
not t o deri ve anot her anal yt i cal expressi on for t he descr i pt i on of t he st r ess- st r ai n
cur ve; r at her some general qual i t at i ve f eat ur es of t he mat er i al behavi or are
est abl i shed, whi ch can be general i zed for mul t i axi al cases.
Fi r s t i t is hel pful t o cl ari fy a poi nt whi ch is basi c for t he under s t andi ng of
f ur t her devel opment . I t concerns t he val ue of t he pl ast i c modul us at t he i ni t i at i on
of pl ast i c def or mat i on f r om an elastic st at e. Accept i ng t he basi c as s umpt i on t ha t
t he t ot al st r ai n i ncr ement d e can be decomposed i nt o a pl ast i c i ncr ement de p and
an elastic one d e e ,
d e ~ - de e + d e p (1)
and since d e = d c ~ / E t , d e e ~ d ( ~ / E ~, de P =- d c ~ / E P , where da is t he st ress i ncr ement ,
and E t , E e, E p are, r espect i vel y, t he t angent , t he elastic, and t he pl ast i c modul i ,
f r om (i) one has:
1 1 1
E - 7 = E - 7 + E-?" (2)
When onl y elastic def or mat i on t akes pl ace, E t = E ~. Therefore, at t he i ni t i at i on
of pl ast i c def or mat i on af t er an elastic st at e, for a s moot h t r ansi t i on f r om t he
elastic i nt o t he el ast o-pl ast i c range, t he i ni t i al val ues of Ep mus t be i nfi ni t e.
I mme di a t e l y t her eaf t er , in t he nei ghbor hood of t he i ni t i at i on of yi el di ng, Ep
assumes a fi ni t e val ue and cont i nues t o change as pl ast i c def or mat i on progresses.
Wh a t is t her ef or e char act er i st i c of t he st ress s t at e at whi ch yi el di ng i ni t i at es, is
exact l y t hi s fi ni t e val ue t ha t EP assumes, af t er t he i nfi ni t e val ue it had at t he
ve r y begi nni ng of t he yi el di ng. Usual l y a ve r y good appr oxi mat i on of t hi s char ac-
t eri st i c fi ni t e val ue of Ep is used as t he val ue of E ' at t he i ni t i at i on of yi el di ng.
As t hi s appr oach appear s t o be reasonabl e, it is adher ed t o in t hi s paper . Thi s
concept is i l l ust r at ed in t he st ress-pl ast i c st r ai n pl ot s of Fi g. 1.
As can be seen f r om Fig. i a, at poi nt A pl ast i c def or mat i on s t ar t s wi t h a val ue
of E~ = t art r 4= oe, where qb is t he angl e shown in t he fi gure. A mor e real i st i c
det ai l of t he mat er i al behavi or is shown in Fi g. i b. Al t hough t he yi el di ng is
A model of Nonlinearly Hardening Materials 177
as s umed t o begi n at A, whi ch is t he t heor et i cal l i mi t of t he el ast i c regi on, t he
pl ast i c behavi or begi ns at A' i nsi de t he yi el d surface. The act ual cur ve is A' A" ,
wher e at A' , i ndeed, Ep = t a n 90 ~ -= ~ and at A" , EP has a fi ni t e val ue. Usual l y
t he cur ve A' A" is a ppr oxi ma t e d b y t he cur ve A' AA" assumi ng ar bi t r ar i l y t ha t
at A, E~ = t an r Thi s is a cont r ol l ed appr oxi mat i on, in t he sense t ha t t he
l ocat i on of A" and t he cor r espondi ng val ue of E p at A, can be sel ect ed as accu-
r at el y as want ed t o a ppr oxi ma t e t he cur ve A' A" b y t he cur ve A' AA" . I n t he
O"
O"
0
~P
A'
~ P
b
:Fig. 1. Schematic explanation of the finite value t hat EP assumes at the initiation
of the yielding
sequel, Ep a t t he i ni t i at i on of yi el di ng will al ways have a val ue whi ch appr oxi mat es
t he t r ansi t i on f r om Ev = co t o EP = fi ni t e i n t he nei ghbor hood of t he i ni t i at i on
of yi el di ng. The general obs er vat i on t ha t yi el di ng s t ar t s at poi nt A' i nst ead of A,
const i t ut es t he mai n poi nt of t he t he or y devel oped b y Pm~nJIPS and col l abor at or s
[9], [10], [11], whi ch i nt r oduces s epar at e yi el d and l oadi ng surfaces. For si mpl i ci t y,
t he concl usi ons of t hi s t he or y will not be used in t hi s paper .
I n Fi g. 2 a t ypi cal mat er i al behavi or is schemat i cal l y shown f or pl ast i c l oadi ng
of consi derabl e magni t ude as well as for unl oadi ng in t he opposi t e sense. Thi s
schemat i c r epr esent at i on, as well as in ot her fi gures t o follow, is based on exper i -
me nt a l r esul t s as t he ones shown in Figs. 3 a nd 4. Not e al so t ha t t he t a nge nt
modul us E t can be consi dered t o be a di r ect measur e of t he pl ast i c modul us EP,
since 1/E t = l IE ~ -~ 1]EP, a nd E ~ is const ant . Ther ef or e, al t hough t he obser-
vat i ons ar e bei ng made in t he a - - e space (Figs. 2, 3 and 4), wher e E t appear s, i n
t he fol l owi ng t he s t at ement s ar e made di r ect l y wi t h r espect t o E p.
The st r ess ver sus st r ai n is pl ot t ed in Fi g. 2. Begi nni ng at 0, t he el ast i c p a r t of
t he st r ess- st r ai n cur ve is OA, and ABD is t he pl ast i c par t . At D el ast i c unl oadi ng
t akes pl ace al ong DD' fol l owed b y pl ast i c r el oadi ng al ong D' D"2,. The line F2, '
r epr esent s a new el ast i c unl oadi ng, and F' F" X a pl ast i c rel oadi ng. Not e t ha t
beyond poi nt B, F" X coincides wi t h BD. I n Fi g. 2 at each l oad r ever sal t hr ee
pa r t s can be di st i ngui shed, each char act er i zed b y t he ma nne r in whi ch E~ changes
al ong it. St ar t i ng f or exampl e f r om poi nt 2,, t he f i r st p a r t F2" r epr esent s t he
elastic behavi or dur i ng whi ch Ep has an i nfi ni t e val ue. The second p a r t 2,'2,"
r epr esent s pl ast i c behavi or . Thi s pa r t is s t r ongl y nonl i near , and 2/p var i es al ong i t
f r om t he val ue i t has a t 2, ' t o t h e val ue i t assumes at 2, ". I n t he sense ment i oned
earlier, at 2" Ep assumes a fi ni t e val ue. Fi nal l y, is t he t hi r d p a r t of t he cur ve
178 Y. F. DA~ALIAS and E. P. PoPov:
F " X , whi ch still r epr esent s pl ast i c behavi or and E~ can be assumed to have a
const ant val ue. Based on ma n y exper i ment s i t can be concl uded t ha t t he t hi r d
por t i ons of t he st r ess- st r ai n curves lie on lines such as X X ' or Y Y ' whi ch pr ovi de
bounds in t he st r ess- st r ai n space. Most of t en t hese lines can be ve r y well appr oxi -
ma t e d b y t wo paral l el s t r ai ght lines as shown in Fig. 2. I n t he pr es ent at i on t ha t
o-

y '
Fig. 2. Schematic illustration of the line bounds in a--e space
follows, t he st r ai ght line appr oxi mat i on of t he bounds ment i oned above will be
kept for si mpl i ci t y, al t hough t hi s is not essent i al for t he gener al devel opment of
t he t heor y. The' essent i al poi nt is t o di st i ngui sh t he second pa r t of t he st ress
st r ai n cur ve f r om t he t hi r d b y t he f act t ha t Ep r api dl y changes al ong t he f or mer ,
and r emai ns essent i al l y cons t ant al ong t he l at t er .
The second por t i on of t he st r ess- st r ai n curve, in whi ch t he l ar gest change of E~
occurs, will now be consi dered in gr eat er detail. To ai d t hi s, t he exper i ment al
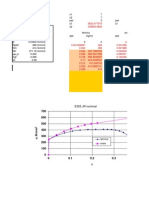
resul t s of cyclic t est s for machi ned speci mens of 60 gr ade st eel ar e shown in
Figs. 3 and 4. The speci mens were 0.436 in. in di amt er , and t he s moot h cyl i ndri cal
por t i ons were 1.90 in. long. Obser vat i ons made on t hi s dat a pr ovi de t he necessar y
i nf or mat i on.
Consi der f i r st Fig. 3. Af t er t he initiM yi el d, t he mat er i al s t ar t s wor khar deni ng.
Dur i ng t hi s phase of l oadi ng, a series of l oad r ever sal s and rel oadi ngs was appl i ed,
and t he resul t s cl earl y mani f est t he exi st ence of t he st r ai ght lines X X ' and Y Y'
ment i oned before, and shown in Fi g. 3 wi t h dashed lines. The r ever se l oadi ng and
rel oadi ng processes gave ri se t o six di st i nct loops, i ndi cat ed on t he di agr am in
circled nmnber s. The poi nt s B~, Ci, Di, Ei , -Fi, where i t akes t he val ues i = 1, 2,
. . . , 6 accor di ng t o whi ch l oop reference is made, are char act er i st i c f or each loop.
B i denot es t he poi nt of elastic unl oadi ng, Gi t he poi nt wher e r ever se pl ast i c
l oadi ng st ar t s, D i t he poi nt of t he new el ast i c unl oadi ng, Ei t he poi nt of pl ast i c
rel oadi ng, and Fi t he poi nt where curves mer ge i nt o t he lines X X ' or Y Y' . For
t he f i f t h l oop t he poi nt F 5 coincides wi t h t he poi nt B6. I t is t o be not ed t ha t
ever ywher e t he el ast i c regi ons r emai n al mos t cons t ant in magni t ude.
Consi der now t he f i r st f our loops and associ at e wi t h t he m a l i ne s egment
A Model of Nonl i nearl y Hardeni ng Materials 179
GIG2G3G4 p a r a l l e l t o XX' , i n t e r s e c t i n g E~Fi a t Gi, wi t h i = 1, 2, 3, 4. I f t hi s
l i ne s e g me n t i s t r a n s l a t e d p a r a l l e l t o XX' , i t i s o b s e r v e d t h a t i t s p a r t s GIG2, G2Gs,
G3G4 r e ma i n c o n s t a n t i n l e n g t h . Thi s i mpl i e s t h a t t h e c ur ve EiFi a r e p a r a l l e l
t r a n s l a t i o n s of e a c h o t h e r a l o n g t h e d i r e c t i o n XX' . The r e f or e , a t c o r r e s p o n d i n g
p o i n t s , l i ke Gi's, t h e EV' s h a v e t h e s a me va l ue a n d a c o mmo n p a r a me t e r mu s t
l O O n
8o.o
60.0
40.0
- ~' O. O
-40.0
-60,0
- 8 0 . 0
A
/
.
, /,? o .:
I i i :i.o
/ Yl T/ Z
Di _ _ ~ D :s
i ~ - - - - - - Y
Y - F e B I I F
Fi g. 3. Experi ment al results for uni axi al random cyclic loading on grade 60 steel specimen
c h a r a c t e r i z e t hi s p r o p e r t y 1. The f a c t t h a t t he s e p o i n t s l i e on a l i ne p a r a l l e l t o XX'
s ugge s t s as s uch a p a r a me t e r t h e i r c o mmo n d i s t a n c e 6 f r o m t h e l i ne XX' . F o r t h e
a n a l y t i c a l f o r mu l a t i o n i t wi l l be n e c e s s a r y t o wo r k on t h e s t r e s s - p l a s t i c s t r a i n s pa c e
i n s t e a d of t h e s t r e s s - s t r a i n s pace, a n d , t he r e f or e , t h e d i s t a n c e 6 i s me a s u r e d i n
Fi g. 3 a l ong t h e d i r e c t i o n of t h e e l a s t i c s t r e s s - s t r a i n l i ne. Th e p r o j e c t i o n of 6 on
t h e p l a s t i c s t r a i n a xi s is zer o, a n d t h e r e f o r e t hi s p a r a me t e r ha s t h e d i me n s i o n s of
s t r e s s onl y, S t a t e d q u a l i t a t i v e l y , Ep i s a n a b s o l u t e l y i n c r e a s i n g f u n c t i o n of 6,
i . e. f or a s ma l l e r 6, Ep a s s u me s s ma l l e r va l ue s . F o r 6 ~ 0, i . e. f or p o i n t s on t h e
XX' or Y Y' l i nes , Ep a s s u me s a l i mi t i n g v a l u e d e n o t e d b y Eo v. E x a c t l y t h e s a me
o b s e r v a t i o n s c a n be ma d e f or t h e CiDi c ur ve s , i = 1, 2, 3, 4, wi t h r e g a r d s t o t h e i r
p a r a l l e l t r a n s l a t i o n . F o r t h e s e eas es t h e d i s t a n c e 6 mu s t be me a s u r e d f r o m t h e
YY' l i ne. Si nc e 6 a s s u me s l a r g e r v a l u e s a l ong CiD~ t h a n a l ong EiF~, t h e c ur ve s
CiDi a r e s t e e p e r t h a n t h e c ur ve s EiFi. The r e f or e , t h e a b s o l u t e v a l u e s of Ep a r e
l a r g e r a l o n g CiDi t h a n a l o n g EIF~. Thi s caus es t h e l oops n o t t o r e t u r n t o t h e s a me
p o i n t , a n d t h e F i ' s do n o t c oi nc i de wi t h t h e Bi ' s b u t u n d e r s h o o t t h e i n i t i a l
p o i n t s . The s a me o b s e r v a t i o n s c a n be ma d e f r o m Fi g. 4 whe r e t h e p a r a l l e l t r a n s -
l a t i o n of t h e c ur ve s a g a i n i s s t r i k i n g l y ma n i f e s t e d .
Ho we v e r , i t i s n o t pos s i bl e t o c onc l ude t h a t t h e p a r a me t e r 6 a l one c a n de f i ne
t h e v a l u e of Ep. Thi s i s e x e mp l i f i e d b y t h e 6 t h l oop. Th e c ur ve C~D6, o r a n y p a r t
of i t , c a n n o t be c o n s i d e r e d as a p a r a l l e l t r a n s l a t i o n of t h e c ur ve s EiFi. Th e c ur ve
C6D6 i s mu c h f l a t t e r t h a n t h e c ur ve s EiFi, a n d , f or t h e s a me v a l u e s of 6, Ep
1 A different stress and pl ast i c st rai n corresponds t o each one of these points. I f stress
and pl ast i c st rai n are used as paramet ers on which EP depends, a suppl ement ary rel at i on
must also be given between t hem expressing t he fact t hat for st at es l yi ng on lines paral l el
t o XX" such as G1G4, E p assumes t he same value, as far as i t s dependence on these two para-
meters is concerned. I n this case t he suppl ement ary rel at i on is simply t he equat i on of t he
line G1G ~. Such a rel at i on reduces t he number of paramet ers from two to one.
180 Y. F. D~-~IAS and E. P. PoPov:
assumes smal l er val ues on it. Therefore, an addi t i onal pa r a me t e r defi ni ng E~ is
i nt r oduced. Thi s pa r a me t e r is t he a mount of pl ast i c wor k Wp = f(~ dev accumul at ed
dur i ng t he pl ast i c def or mat i on pr i or t o t he el ast i c def or mat i on pr eceedi ng t he
cur r ent pl ast i c st at e. For sof t eni ng mat er i al s, Ep is a decreasi ng f unct i on of W p.
Conversel y, for har deni ng mat er i al s, Ep is an i ncreasi ng f unct i on of W p. I n ot her
words, i t is assumed t ha t t he mat er i al exhi bi t s f adi ng memor y, r emember i ng onl y
what has happened dur i ng t he mos t r ecent l oadi ng hi st or y.
The t wo par amet er s d and W ~ are suffi ci ent t o det er mi ne t he behavi or of a
mat er i al such as shown in Figs. 3 and 4. ]for exampl e, consi der t he curves C6D 6
and E3F 3 in t he 6t h and 3r d l oops of :Fig. 3. He r e it can be seen t ha t t he pl ast i c
modul us al ong t hese t wo cur ves is i nfl uenced not onl y b y t he di st ance d, but al so
b y t he pl ast i c wor k done i n t he r espect i ve pr oceedi ng half-cycles. For t hi s sof t eni ng
mat er i al , t he pl ast i c wor k done al ong EGB~ is consi der abl y gr eat er t ha n t ha t al ong
CaD 3. For t hi s r eason t he cur ve C6D6 is f l at t er t ha n t he cur ve EsFa. I n f act at De,
Ep has al r eady r eached t he val ue E0 p due t o t he i nfl uence of W' , even before d
becomes zero. At t hi s poi nt f or self consi st ency of t he pr oposed model i t is necessar y
t o i nt r oduce t he r est r i ct i on t ha t EP can never become smal l er t ha n E0< The same
l oops 3 and 6 also show t ha t i t is not possi bl e t o defi ne Ev usi ng t he pa r a me t e r W p
alone. The cur ve EaF a whi ch at t he begi nni ng is less f l at t ha n C6D6 becomes
equal l y f l at much f as t er as i t appr oaches t he l i ne XX' . Thi s can be a t t r i but e d t o
t he f act t ha t t he i nfl uence of d, as i t t ends t o zero, becomes domi nant on t he val ue
of E< Anal ogous concl usi ons can be r eached b y consi deri ng loops 5 a nd 6. At t he
begi nni ng t he cur ve EsF 5 is st eeper t ha n EGF6, since t he pl ast i c wor k done al ong
CsD 5 is much less t ha n t he pl ast i c wor k done al ong 06D6. As t hese curves appr oach
t he line YY' , t he i nfl uence of t he pa r a me t e r ~ becomes domi nant and t he curves
t end t o coincide. An exami nat i on of t he loops in Fi g. 4 rei nforces t hese conclusions.
Consi der in t hi s di agr am t he t wo gr oups of t hr ee loops each denot ed b y enci rcl ed
8O
40
LU 0
m
--40
-80
J ' 30 ' 4 5 1
TRAiN {I0 IN/IN)
~'ig. 4. Experimental results for uniaxial cyclic loading on grade 60 steel specimen
A Model of Nonlinearly Hardening Materials 181
number s 1 and 2. l~or each group, t he t i ps of t he t hr ee loops is mar ked conse-
cut i vel y 1, 2, 3. I n each group, t he loops havi ng t he t i p number 1 are cl earl y
f l at t er t ha n t he ot her t wo, and t hi s agai n can be at t r i but ed t o t he f act t ha t t he
pr i or pl ast i c wor k in t ensi on f or t hese loops was gr eat er t ha n f or t he l at er ones.
Consider l ast l y t he fi rst f our loops of Fig. 3. The curves Ei Fi , i ~ 1, 2, 3, 4,
whi ch are near l y identical, are paral l el t r ansl at i ons of each ot her. The pl ast i c
wor k done in t he half-cycles preceedi ng t hese curves is near l y equal. Therefore,
onl y 6 becomes t he par amet er whi ch di fferent i at es t he val ue of EP along t hese
E~Fi curves.
Recapi t ul at i ng, i t is consi st ent l y obser ved f r om a series of uni axi al cyclic l oad
exper i ment s, t ha t t he pl ast i c modul us Ep can be det er mi ned by t wo par amet er s, a
stress par amet er and a st r ai n par amet er . The di st ance 6 defi ned earlier has t he
measure of stress, and is t he stress par amet er . The st rai n par amet er is associ at ed
wi t h t he pl ast i c wor k done dur i ng t he pl ast i c def or mat i on pr i or t o t he elastic
def or mat i on preceedi ng t he cur r ent pl ast i c st at e. Al t er nat i vel y, t he correspondi ng
pl ast i c st r ai n ma y be used i nst ead of t he pl ast i c work. As a closing not e, i t must be
added t ha t f or gr eat er gener al i t y a change of t he di st ance bet ween t he t wo
boundi ng lines XX' , Y Y ' must be allowed, if necessary.
4. S o me Cyc l i c Lo a d i n g P h e n o m e n a
Bef or e pr oceedi ng wi t h t he anal yt i cal f or mul at i on of t he model, i t is shown in
t hi s sect i on how some phenomena associ at ed wi t h cyclic l oadi ng are qual i t at i vel y
pr edi ct ed on t he basis of t he obser vat i ons made earlier. An ext ensi ve s t udy of
t hese phenomena is gi ven in references [21] and [22].
The phenomenon of cyclic creep in uni axi al l oadi ng is shown schemat i cal l y in
Fig. 5. The st ress vari es bet ween t he bounds ~1 and ~2 wi t h a mean st ress of
(a2 - - r # 0. Assume t ha t cyclic l oadi ng st ar t s at poi nt Ax, and consecut i vel y
progresses t o poi nt s A2, A3, A4 etc. kl is t he poi nt in st ress space where yi el di ng
i ni t i at es i n t he course of appr oachi ng t he bound r and k2 is t he correspondi ng
poi nt f or t he bound r Bet ween k~ and ~ or k2 and or2, Ev changes accordi ng t o t he
di st ance ~ of t he correspondi ng poi nt s f r om Y Y ' or XX' , respect i vel y, and t he
pl ast i c wor k done dur i ng t he previ ous pl ast i c def or mat i on. I t is assumed t ha t t he
r el at i on gi vi ng Ev as a f unct i on of t he di st ance ~ is t he same whet her t he di st ance
is measur ed f r om Y Y ' f or t he regi on kl(ri, or f r om X X ' f or t he regi on k2~2. I t has
been al r eady not ed t hat t he closer t he poi nt is t o t he X X ' (or YY' ) line, t he smal l er
t he val ue of Ev. Assume now t ha t at t he begi nni ng, t he stress st at es l yi ng o n ]c2o" 2
cor r espond t o t he poi nt s in t he st ress-st rai n space which have a smal l er di st ance
f r om X X ' t han t he correspondi ng poi nt s of t he stress st at es on klal have f r om YY' .
On t he ot her hand, in each case t he pl ast i c wor k done before l oad r ever sal is
appr oxi mat el y equal. For t hese conditions, Ev will be gr eat er f or t he stress st at es
l yi ng on k1r t ha n f or t he ones on k2~2, and f or cyclic l oadi ng t he loops will not be
closed and will progress t o t he r i ght as shown in Fig. 5. Thi s cl earl y exemplifies t he
phenomenon of cyclic creep. As a r esul t of t hi s progress t o t he ri ght , t he above
ment i oned di st ances of t he stress st at es o n ] Q o " 1 and ]C2o" 2 t e nd t o become equal
wi t h t he consequence t ha t EP' s also become equal and t ha t t he loops converge t o a
st abl e closed loop.
182 Y. F. DAFALIAS and E. P. PoPov:
O-
k2
k l
a"
f X
A , A 3 A s A ~
~Y
Fig. 5. Schematic representation of cyclic creep
Anot her cyclic phenomenon is that of cyclic softening. I n Fig. 6 this pheno-
menon is shown schemat i cal l y f or t he uni axi al case. For t hi s case t he st ress
bounds are symmet r i c, r and --a0, wi t h r espect t o t he origin. I n t he course of
cyclic loading, t he loops become l arger, and t he st ress-st rai n curves in t he pl ast i c
range become f l at t er . I n t er ms of t he pr esent model t hi s is expl ai ned as follows.
The pl ast i c work WP done duri ng t he consecut i ve half-cycles t ends t o become
progressi vel y larger. For soft eni ng mat eri al s t hi s makes t he subsequent pl ast i c
response curves f l at t er . On t he ot her hand, t hi s m~kes t he di st ance c~ become
l arger, t endi ng t o make t he curves st eeper. Fi nal l y, t he par amet er s 8 and Wp
count erbal ance, resul t i ng in ~ st abl e loop. I t mi ght happen t ha t Es reaches t he
limiting val ue E0 p before ~ ---- 0, but since Es is not per mi t t ed t o become smal l er
t han E0 p, t hi s can also stabilize t he process.
Fig. 6. Schematic representation of cyclic softening
A Model of Nonlinearly Hardening Materials 183
The phenomenon of cyclic hardening can also be explained on the basis of the
proposed model. I n Fig. 7 a cyclic loading diagram is shown for a hardening
material with strain bounds The increase on Wv makes the curves steeper,
but on approaching the bounding lines XX' , Y Y', the paramet er 6 becomes smaller,
which tends to flatten the curves. When the two effects balance, the process is
stabilized exhibiting a closed loop. For certain cases where hardening (softening)
phenomena are strongly exhibited, an additional allowance of change of the dis-
tance between the two bounding lines XX' , YY' is necessary for a better de-
scription of the above mentioned phenomena. However, for simplicity, this will
not be considered in the sequel.
r
:A3
X ' , A,
/ / ? '. , '
- ~EO ~ ~ o
E"
T / /
y ' ~
Fig. 7. Schematic representation of cyclic hardening
5. Uniaxial L o a d i n g
The basic observations needed for the development of the model have been
stated already. However, t hey are not in an appropriate form for analytical
formulation and generalization for multiaxial loading. For this purpose it is
necessary to formulate the basic concepts in stress space, and not Jn the stress-
strain space, as has been done hereto. This is accomplished by projecting the
stress-plastic strain space onto the stress space, which in the uniaxial case is the
a-axis, Fig. 8 3 .
Let ZZ' be the stress-plastic strain pat h which is followed during the plastic
loading. Points A and A' are two neighboring states, both lying on ZZ' . I n the
sequel, reference to these points will be made as state A and state A' . Quantities
associated with state A are denoted by unprimed symbols, and the corresponding
quantities for state A' are primed.
If at A a complete unloading takes place, the unloading pat h would be AA,
2 In this section the formulation takes place in a--sP space. The transformation from
a e to a--eP is linear, and it introduces exactly the same concepts of the bounding lines
XX' , YY" and the distance 6 in a~sP. However, dt is now vertical and equal to the projection
on a-axis of its representation in a--e space. In fact, if the value of this parameter is denoted
by 6 for the a--e space, and by 6 for the a--sp space, it is (~ = $ sine e, where tanq~ e = E%
184 Y. F. ])AFALIAS and E. P. PoPov:
whi ch is elastic. The pr oj ect i on of A, A ont o t he a-axi s are t he poi nt s a, 5, whi ch
pl ay t he rol e of t he l oadi ng surface associ at ed wi t h s t at e A for t he uni axi al ease.
The line AA can be consi dered as pa r t of t he l ar ger s egment BB, whi ch is f or med
by ext endi ng AA unt i l i t i nt er sect s t he lines X X ' and Y Y ' . The pr oj ect i on of BB
ont o t he a-axi s gi ves t he l i ne segment bb whi ch encloses t he el ast i c segment aS.
Poi nt s/ c, r on t he a-axi s are, r espect i vel y, t he cent er s of a5 and bb, and ar e also
t he pr oj ect i ons of K, R on t he a-axi s. Anal ogous s t at ement s appl y f or s t at e A ' .
Af t er t he t r ansi t i on f r om st at e A t o s t at e A' due t o a st ress i ncr ement da, t he
el ast i c regi on a5 moves t o a new posi t i on a ' 5' and t he encl osi ng line segment bb
moves t o b' b' .
0 "
b'
Ob( 84
X' a
d'
k
o
y J
X
B , ~ an 4~~
K ' . / . . , . Ep = tan
/ Y
- ~ w p E
Fig. 8. Projection of the ~--ep space onto the s~ress space for ~he uniaxial case
Denot e b y d~ t he i ncr ement al di spl acement kk' of t he cent er k of t he i nner
line segment (elastic region), and b y dfi t he cor r espondi ng quant i t y st ' f or t he
cent er r of t he out er line segment . Let da and des be, r espect i vel y, t he st ress and
pl ast i c st r ai n i ncr ement s, and S and clS, t he l engt h and t he i ncr ement of l engt h of
t he i nner line segment (elastic region). :For t he expansi on of t he elastic regi on
d S > 0 and for cont r act i on dS < 0. Then, if EP is t he val ue of t he pl ast i c modul us
at s t at e A, t he following r el at i ons hol d
d(7 = Ep deP, (3)
= da - - ~ d S . (4:) d~
25
A Model of Nonlinearly Hardening l~'[aterials 185
T h e poi nt R is mo v i n g i n a - - s P space al ong t he l i ne n n ' whi ch is f i xed a n d
par al l el t o t he di r ect i on of t he X X ' , Y Y ' lines. Ther ef or e, si nce d f l = r r ' a n d
t a n qb 0 = Eo p, us i ng (3) one has
a n d f r o m (4) a n d (5),
E~ d
d f l ~ - Eo ~ ds P = ~ a
( ~ )
Al l t he a bove i nc r e me nt a l r el at i ons ar e wr i t t e n f or s t at e A , a n d t her ef or e t he
val ue of Ep is d e t e r mi n e d b y t he di s t ance 6 ~ a b -= A B a n d t he a ppr opr i a t e val ue
of W p. At s t at e A' t he val ue of E p is d e t e r mi n e d b y 6' --~ a ' b ' ~ A ' B ' a n d t he s a me
val ue of W p. Ther ef or e, i t is desi r abl e t o ha ve a n expr es s i on of 6' i n t e r ms of ($
whi ch fol l ows f r o m
a b ' ~ a a ' d - a ' b ' ~ a b -4- b b ' (7)
whe nc e wi t h t he ai d of (5) a n d a a ' ~ - dcr, a b ~ - 6 , a ' b ' =- (~' a n d b b ' ~ - d f i ,
6 ' - ~ = d ~ = \[ E~ - - 1 ) d a . ( 8 )
E p is gi ven b y a r el at i on of t he f or l n
E p : ~p( ( ~, Wp), (9)
wi t h E0 v ~ ~P(0, WP). The f unc t i on ~P i s: (i) a n a bs ol ut e l y i ncr eas i ng f unc t i on
of 6, (ii) a n a bs ol ut e l y decr eas i ng f unc t i on of W p if t he ma t e r i a l sof t ens, a n d
(iii) a n a bs ol ut e l y i ncr eas i ng f unc t i on of W p if t he ma t e r i a l ha r de ns . W p is t he
pl as t i c wo r k dur i ng t he hal f - cycl e pr e c e e di ng t he c u r r e n d pl as t i c s t at e. The
r es t r i ct i on t h a t En > E0P f or a n y (~ a n d W p is as s umed. Si nce S is a f unc t i on of
a s cal ar q u a n t i t y , us ua l l y t he pl as t i c wor k, d S can be de t e r mi ne d. I f , dur i ng a
pr ocess, S is c ons t a nt , al l r el at i ons a bove hol d t r ue wi t h dS ~ 0.
Th e i nc r e me nt a l pr oces s f or a uni axi al case is c ompl e t e l y de t e r mi ne d f r o m
t he a bove set of equat i ons . I n d e e d , gi ven d~, Wp a n d 6, t he d s p , d ~ , d f i ar e obt a i ne d
f r o m (3), (4), (5) us i ng t he val ue of E p f r o m (9), a n d t he val ue of d S f r o m a r el at i on
f or S. F o r t he n e x t i nc r e me nt , 6' is obt a i ne d f r o m (8) a n d a new val ue of Ep is
o b t a i n e d f r o m (9). Th e n t he pr oces s is r epeat ed. I f el ast i c unl oa di ng t akes pl ace,
t hen, f or t he n e x t pl as t i c l oadi ng, a new val ue of W p ent er s i n (9). Thi s di s-
c ont i nuous c ha nge f r o m one val ue of Wp t o a not he r , ma y be t he cause of a di s-
c o n t i n u i t y i n t he val ue of Ep f or t he s ame 6 ; t hi s is t he cons equence of t he si mpl i -
f yi ng a s s u mp t i o n of r e t a i ni ng onl y t he mo s t r e c e nt pr evi ous W p i n t he ma t e r i a l
me mo r y .
Pi ct or i al l y, t he i mage obt a i ne d is t h a t of t wo l i ne s e gme nt s on t he a- axi s, t he
one encl osi ng t he o t h e r ; whe n t he i nne r one move s due t o a n i nc r e me nt of st r ess da,
t h e out e r one al so move s i n t he s a me sense b u t a t a sl ower r at e. So e ve nt ua l l y, i f
t he mo t i o n cont i nues i n t he s ame sense, t he i nne r s e gme nt r eaches t he out er ,
whe nc e t h e y c ont i nue t o mo v e t oge t he r . I n t he cour se of t hei r mot i on, t he di s t ance
($ c ha nge s c ont i nuous l y, a n d Ep changes a c c or di ngl y as a f unc t i on of 6, t e ndi ng t o
t h e mi n i mu m val ue of E0 v a t ~ ~ 0. I t is al so possi bl e t h a t due t o t he s t r a i n
186 Y.F. DAt~ALIAS and E. P. PoPov:
parameter W p, Ep assumes the value of Eo p with c$ 4= 0. Then from (8) one has
~' = d, and the two line segments move at the same rate without being in contact.
This corresponds to the possibility t hat the plastic stress-strain curve becomes
parallel to the XX' , YY' lines before reaching them.
6. Multiaxial Loading
The generalization of the model to higher dimensions is straightforward.
Although now the stress space is 6-dimensional, all the essential features can be
shown in a 2-dimensional space as in Fig. 9 a. The elastic region is represented by
the interior of the loading surface, shown for simplicity as a circle with the center
at k. This corresponds to the inner line segment on the ~-axis of the uniaxial case.
The outer line segment is represented by another surface in the stress space,
shown again as a circle with the center at r, enclosing the yield surface. This
second surface in the stress space will be called the bounding surface, from the
fact t hat the yield surface is constrained to move always within this surface,
which also moves in the stress space.
I n the uniaxial ease the plastic state A was determined by two points on the
~-axis. Point a represented the stress state, and point b defined d = ab, which
determined the value of Ep at state A t hrough Ep =/~P(d, WP). Aecordingly, in
Fig. 9 a point a is taken on the yield surfaee, and ~oint b on the bounding surface.
C
(1
(13
(12 ~
b
Fig. 9. Schematic representation of a loading and a bounding surface and ilIustration
of their motions
I n this manner the distance d = ab, which in t urn determines the value of tile
generalized plastic modulus at a for the multiaxial ease. However, there are now
two questions in connection with this generalization. The first is how to determine
the bounding surface in the multiaxial case. The second, with the position of the
loading and bounding surfaces known, which point b on the bounding surface
corresponds to point a on the loading surface, and how the distance d is defined in
a 6-dimensional space. The answers to these questions are interrelated, since the
determination of the distance b indirectly also defines the bounding surface. At
present no experimental evidence is available to answer this question. Therefore,
A Model of Nonlinearly Hardening Materials 187
i t is necessar y t o make some si mpl i f yi ng assumpt i ons, whose rel i abi l i t y is based on
t he f act t ha t t he resul t s r educe t o t he known uni axi al ease. For t hi s pur pose a
surface encl osi ng t he l oadi ng surface is chosen as t he boundi ng surface. Thi s
surface can or di nar i l y be t a ke n congr uent t o t he l oadi ng surface.
:For t he second quest i on r ai sed above ma n y as s umpt i ons are possible. For
exampl e, if t he t wo surfaces are congr uent , b can be t he poi nt cor r espondi ng t o a
wi t h r espect t o t he congr uency; or b can be obt ai ned b y t he i nt er sect i on of t he
nor mal t o t he l oadi ng surface at a wi t h t he boundi ng surface; or si mpl y b can be
t he i nt er sect i on of / ca wi t h t he boundi ng surface as shown in Fig. 9 a. As for t he
di st ance 8, it ma y be gi ven b y t he usual Eucl i di an met r i c, i.e. if aij are t he coordi-
nat es at a and ~ j t he coor di nat es at b, t hen
(~o)
I f now K is t he gener al i zed pl ast i c modul us f or t he mul t i axi al case, assumi ng
t he associ at ed fl ow rul e, and t ha t t he pl ast i c st r ai n i ncr ement d e ~ j is pr opor t i onal
t o t he pr oj ect i on da of t he st ress i ncr ement daq on t he uni t nor mal n i j t o t he
l oadi ng surface, one has
1
d e ~ . ~ - - ~ d ~ n ~ j . (11)
The val ue of K is gi ven b y a r el at i on ol t he f or m
K = f : ( ~, W~) , ( 1 2 )
where t he f unc t i on/ ~ has t he same pr oper t i es as t he f unct i on i~p f or t he uni axi al
case. The pl ast i c wor k now is defi ned as W ~ = d e , j , where t he i nt egr at i on is
ma d e in t he st r ai n space al ong t he l oadi ng p a t h dur i ng t he pl ast i c def or mat i on
pr i or t o t he elastic def or mat i on pr eceedi ng t he cur r ent pl ast i c st at e.
The l oadi ng surface can t r ans l at e and possi bl y def or m in t he st ress space
accordi ng t o a ny har deni ng rul e consi dered appr opr i at e. Si mul t aneousl y, t he
boundi ng surface t r ansl at es in t he st ress space accor di ng t o a rul e Which will be
speci fi ed l at er. The boundi ng surface ma y also def or m; an expansi on f or exampl e
of t he boundi ng surface woul d cor r espond t o an i ncrease in t he di st ance bet ween
t he t wo boundi ng lines X X ' , Y Y ' in t he uni axi al ease. The rul e of t r ans l at i on of
t he boundi ng surface shoul d al l ow for t he following gener al feat ures. I t is possi bl e
f or t he l oadi ng surface t o cont act t he boundi ng surface, but not i nt er sect it. I n
general , t he boundi ng surface t r ansl at es at a sl ower r at e t ha n t he l oadi ng surface.
I f t he pl ast i c l oadi ng cont i nues af t er t he cont act of t he t wo surfaces, t hey move
t oget her bei ng in cont act . I f elastic unl oadi ng t akes pl ace and is fol l owed b y a
pl ast i c l oadi ng in a di f f er ent di rect i on, t he l oadi ng surface det aches f r om t he
boundi ng surface, a nd t he t wo surfaces agai n move at di f f er ent r at es and di rec-
t i ons, unt i l pe r ha ps t he y j oi n agai n at a di f f er ent poi nt . I t is i mpor t a nt t h a t t he
poi nt of cont act al so r epr es ent s t he st ress st at e. :For t hi s poi nt in common t o t he
t wo surfaces, ~ ~ 0 and K =/ ~ ( 0 , Wp ) = K0, in di r ect cor r espondence t o
Ep = ~P(0, W p) = EoP f or t he uni axi al case. I f t he poi nt on t he l oadi ng surface
r epr esent i ng t he st ress s t a t e is not al so t he cont act poi nt , t he fol l owi ng i ncon-
si st ency woul d r esul t ; i t woul d be possi bl e t o follow a st ress pa t h such t ha t t he
188 Y. F. DAFALIAS and E. P. PoPov:
t wo surfaces move t oget her j oi ned at t he same poi nt , wi t h t he poi nt r epr esent i ng
t he st ress st at e on t he l oadi ng surface never r eachi ng t he boundi ng surface. For
t hi s s t at e poi nt ~ ~= 0, and t her ef or e wi t h t he val ue of WP f r om t he pr evi ous
l oadi ng, K coul d never a t t a i n t he val ue K o whi ch i t shoul d reach. Fi nal l y, t he rul e
of t r ansl at i on of t he boundi ng surface shoul d al ways yi el d t he known resul t s for
t he uni axi al case. Therefore, t he anal yt i c f or mul at i on of t hi s rul e will be obt ai ned
b y a di r ect gener al i zat i on of t he cor r espondi ng expressi ons in t he uni axi al case.
For t he pur poses at hand, (5) can be r ecast i nt o t he fol l owi ng form,
df l = Eo v dsP ~- E p dsP - - ( EP - - Eo p) deP ~- d(~ - - ( E~ - - Eop) de p. (13)
I n t hi s equat i on t he st ress i ncr ement d~ is t he i ncr ement al di spl acement in t he
st ress space of t he poi nt of t he l oadi ng surface whi ch r epr esent s t he cur r ent
st ress st at e. I t shoul d be not ed t ha t t hi s qua nt i t y has a di f f er ent meani ng t ha n da
i n (11), where i t appl i es t o t he mul t i axi al case. Fig. 9b i l l ust r at es t he qua nt i t y
cor r espondi ng t o da of (13) in mul t i di mensi onal st ress space. Poi nt a of t he
l oadi ng surface r epr esent s t he cur r ent st ress st at e. I f t he st ress i ncr ement is
denot ed b y d6, t he vect or aa~ r epr esent s i t ; t he vect or aas r epr esent s t he pr o-
j ect i on of d 6 in t he uni t nor mal n; and t he vect or aa s r epr esent s t he i ncr ement al
di spl acement of a whi ch is in t he di r ect i on of a uni t vect or v. Not e t ha t t he new
st ress s t at e is r epr es ent ed b y as , while t he poi nt a of t he l oadi ng surface moves
t o as. The vect or aa3 cor r esponds t o t he qua nt i t y da of (13) in t he uni axi al case.
Wi t hi n a second or der appr oxi mat i on i t can be as s er t ed [6] t ha t aa2 ~- d(~ n is t he
pr oj ect i on on n of bot h aa~ a n d aa 3. Therefore, if ~o is t he general i zed angl e bet ween
n and v, and since n 9 v ---- n~jv~j ---- cos ~o,
d(y
aa 3 = v . (14)
Cos o)
Thi s r el at i on is t he general i zed expressi on for da of (13). For t he gener al i zat i on
of t he second pa r t of (13) a modi f i cat i on of an i dea ori gi nal l y empl oyed b y MRoz
[18] is used. Denot e by c in Fig. 9a t he poi nt on t he boundi ng surface where t he
out war d nor mal t o i t has t he same di r ect i on as t he nor mal t o t he l oadi ng surface
at a. Then denot i ng b y / t t he uni t vect or al ong a c , t he i ncr ement al t r ans l at i on
of t he boundi ng surface al ong ~ woul d event ual l y sat i sf y t he r equi r ement t ha t
t he poi nt of cont act is at t he same t i me t he cur r ent st ress st at e s . Therefore, in
general i zi ng (13), a t r ans l at i on al ong 9 is assumed for t he second par t . More
preci sel y, usi ng (11), (14) and t he above as s umpt i on
df i i i = cosd(Ie9 vi i - - ( K - - Ko ) (ds~mn dsPmn) 1/2 ~tii
= g~ [ - ~ , ~ - ( 1 - - ~ ) ~ j ] .
(15)
Thi s equat i on cor r esponds t o (5) of t he uni axi al case. A r el at i on cor r espondi ng
t o (8) of t he uni axi al case requi res a specific f or mul at i on, and is not gi ven in
3 lVI~oz uses this approach to define a kinematic rule for the loading surface; no specific
kinematic rule is assumed in the present development.
A Model of Nonlinearly Hardening Materials 189
t hi s gener al pr esent at i on. Obser ve t ha t if t he l oadi ng surface moves as a ri gi d
body, t he t e r m da vii/cos co is al so t he i ncr ement al di spl acement dai j of t he cent er
of t he l oadi ng surface. Thi s will be di scussed f ur t her in t he following section.
I n such a ease, when t he t wo surfaces come i n cont act , f or t he poi nt in common
= 0 and K = Ko , and (15) yi el ds df l i j = d g i i , i.e., t hey move t oget her at t he
s ame r at e 4. Si mi l ar l y t o t he uni axi al case, i t is also possi bl e t ha t K t akes t he
val ue K0 before t he l oadi ng surface reaches t he boundi ng surface, and t hen t he
t wo surfaces move at t he same r at e and di rect i on wi t hout bei ng in cont act . Cer-
t ai nl y, wi t h dal i and dtS~i comput ed, i t is possi bl e t o fi nd t he new r el at i ve posi t i on
of t he t wo surfaces. Taki ng also i nt o account t he possi bl e def or mat i on of t he
t wo surfaces, t he new di st ance (~' can be f ound bet ween t he poi nt on t he yi el d
surface r epr esent i ng t he new st ress st at e, and t he correspondi ng poi nt on t he
boundi ng surface. Then wi t h b' and an appr opr i at e val ue of W~, t he new val ue
at K is obt ai ned f r om (12), and is used in t he ne xt st ep.
7. Appl i cat i on t o Speci fi c Ha r de ni ng Laws
I n or der t o i l l ust r at e t he above f or mul at i on, t he ki nemat i c model s of PlCAO~
and ZIEOL~I~ will be consi dered in connect i on wi t h t he pr oposed model .
(i) P r a g e r ' s Mo d e l
The i ni t i al l oadi ng surface is gi ven by
l o ( ~ i s ) = 0 ( a )
and t he subsequent l oadi ng surfaces b y
l (a~j , ~xij) = / o ( a i j - - ai~) : 0 (b)
where
dccii = c ds~-. (c)
The associ at ed fl ow l aw is gi ven b y (1U.
The gr adi ent of/ (a~i ) wi t h r espect t o aij is wr i t t en as
8 !
- - = gnij (d)
8ai i
where n~. is a uni t out war d nor mal t o t he l oadi ng surface, and g is t he nor m of
t he gr adi ent , i.e. g = [(~//~aij) (~[/~aij)] 1/2.
I t can al so be shown t ha t
8 t _ 8 !
8~ij ~aij (e)
Fr om (11), (c), (d), (e), and t he consi st ency condi t i on d / = O,
d/ ~! d~j + 81 1
: ~ i j ~ d~i~ = g n i j da~j - - gni~c - - ~ d a n i j ~ 0
and since da~j n~i = d~ and n~in~i = 1, i t follows t ha t c = K.
4 In general, after contact first occurred between the two surfaces, the point of contact
remains on the stress path.
Act a Mech. XXI ] 3 14
190 Y. F . D~ALIAS and E. P. PoPov:
T h e r e f o r e , wi t h t h e a i d of (11),
d ~ j = ~ d ~ j = d~ n ~ . (f)
I n t h i s c a s e ~ i = n ~ a n d cos co = 1, h e n c e (15) y i e l d s
d f l i j : d c ~ j - - d a ( 1 - - - - ~ ) # i , . (g)
Eq s . ( f ) a n d (g) c o r r e s p o n d d i r e c t l y t o (4) a n d (6) of t h e u n i a x i a l c a s e wi t h
d S ---- O .
(ii) Z i e g l e r ' s m o d e l
Zi e g l e r ' s mo d i f i c a t i o n o f P r a g e r ' s mo d e l s u g g e s t i n s t e a d of d~i j = c de, j , t h e
r e l a t i o n
d~i j = d#(a~j - - ~ ) . (h)
Fig. 10. Schemat i c r epr esent at i on of t he loading and boundi ng surfaces for[Zi egl er' s model
A l o a d i n g a n d a b o u n d i n g s u r f a c e a r e s h o wn i n Fi g. 10, f r o m wh i c h
k a = a i j - - a ~ j = ~ u i j (i)
wh e r e ui i i s t h e u n i t n o r ma l a l o n g t h e r a d i u s ka, a n d ~o i s t h e n o r m of t h e r a d i u s .
Wh e n c e (h) y i e l d s
dcqj = d # ~ui~. (j)
F r o m (j ), (d), (e), a n d d / = 0 ,
~ (Y O ~9~
a n d
~ , a - - - ~ n i j d a ~ ] . (k)
~ n i i u i i
A Model Of Nonlinearly Hardening Materials 191
Since n~j daij = d a , ni ~ui j -= In] [u] cos 0 = cos O, where 0 is t he general i zed angl e
bet ween t he nor mal t o t he l oadi ng surface at a and t he radi al di rect i on k a as
shown in Fig. 10, t he above r el at i on f or d# becomes
and f r om (j) and (1),
da
@ - (1)
~) cos 0
d~ii = cos 0 ui j . (m)
I n t hi s case vii ~-- uij and 0 ~ o.), hence (15) yields,
(n)
The rel at i ons (m) and (n) correspond t o (4) and (6) f or t he uni axi al case, and t o (f)
and (g) of Pr ager ' s model.
8. General Conclusions
The pur pose of t hi s paper was t o pr esent a t echni que of account i ng for t he
di f f er ent phenomena mai nl y associ at ed wi t h cyclic mul t i axi al l oadi ng i n t he
pl ast i c range. I t is recogni zed t hat in uni axi M loading, t he changes in t he pl ast i c
modul us dur i ng t he course of pl ast i c def or mat i on is t he mai n cause of t he phe-
nomena such as cyclic creep, soft eni ng and har deni ng. Fol l owi ng t he same line
of reasoni ng, based on observat i ons of ma ny exper i ment al resul t s f or t he uni axi al
case, general i zat i ons for t he mul t i axi al case were made. One of t hese general -
i zat i ons yi el ded t he concept of t he boundi ng surface in t he stress space, whi ch
encloses t he yi el d surface, and in general moves and deforms si mul t aneousl y
wi t h i t in a coupl ed manner . The r el at i ve posi t i on of t hese t wo surfaces and t he
pl ast i c work W p defi ned earlier, det er mi ne at each stage t he val ue of t he pl ast i c
modul us al ong t he yi el d surface. The dependence of t he pl ast i c modul us K, in
t he mul t i axi al case, on t he di st ance ~ bet ween correspondi ng poi nt s on t he l oadi ng
and t he boundi ng surface needs exper i ment al veri fi cat i on. The pl ast i c modul us
assumes a const ant val ue f or poi nt s on t he boundi ng surface.
The pr oposed model posesses consi derabl e general i t y. For l ack of exper i ment al
evi dence i t has not been specialized f or any par t i cul ar mat eri al , i t is believed,
however, t hat t he gener al i t y and fl exi bi l i t y of t he model is such t ha t i t can be
adj ust ed t o t he exper i ment al resul t s once t hey become available. :No specific
ki nemat i c and def or mat i on law f or t he l oadi ng surface was assumed in t he general
devel opment . Thi s is del i barat e, as i t ]eaves free t he choice of a har deni ng rul e
f or specific cases. Fi nal l y, t he i ncr ement al anal yt i cal f or mul at i on of t he model
is ve r y simple, and appear s t o be especially sui t abl e f or use in solving pr obl ems
numeri cal l y, wi t h l i t t l e addi t i onal effort .
Acknowledgements
The work was suppor t ed in par t by cont r act s DAA 21-72-C-0729, NSFGI - 36387,
and by Lockheed Missiles and Space Company. Mr. M~S~ALL MA, a gr aduat e
st udent , pr ovi ded t he dat a f or Fig. 4.
14"
192 Y. ~. DAFALIAS and E. P. PoPov: A Model of Nonlinearly Hardening Materials
References
[1] HILL, R. : The Mat hemat i cal Theory of Pl ast i ci t y, 1st ed., p. 24. Oxford Uni versi t y
Press. 1950.
[2] HOgGE, P. G., 0R.: The Theory of Piecewise Li near Isot ropi c Pl ast i ci t y. IUTAM Col-
loquium Madrid, 1955.
[3] IS~INSK~, A. I v. : General Theory of Pl ast i ci t y wi t h Li near St r ai n I-Iardening. Ukr.
mat . zh. 6, 314 (1954).
[4] Pa~ow~, W. : A New Method of Anal yzi ng Stresses and Strains in Work-Hardeni ng
Pl ast i c Solids. J. App. Mech. Trans. ASME 78, 493 (1956).
[5] SmELl), R. T., and H. ZIEGI,E~: On Prager' s Hardeni ng Rule. ZAMP 9a, 260 (1958).
[6] ZIEOL]~, H. : A Modification of Prager' s Hardeni ng Rule. Quart. Appl. Math. 17, 55
(1959).
[7] ED]~LlV~, F. , and D. C. D~UCKE~: Some Extensions of El ement ar y t )l ast i ci t y Theory.
J . F. I . 251, 581 (1951).
[8] BXLTOV, A., and A. S~wczITK: A Rule of Aniso~ropic ~ar deni ng. Act s Mech. 1, 81
(1965).
[9] PEI uPs, A., and R. L. SIE~KOWSKI: On t he Concept of t he Yield Surface. Act~ Mech.
1, 29 (1965).
[10] JusTvssO~, J. W. , and A. PHILLIPS: St abi l i t y and Convexity in Pl ast i ci t y. Act s Mech.
2, 251 (1966).
[11] EISE~BV, RG, M. A., and A. PHILUPS: A Theory of Pl ast i ci t y wi t h Non-Coincident Yield
and Loading Surfaces. Act s Mech. 11, 247 (1971).
[12] K~]),~S~]~vITc~, I v. I. , and V. V. NovozmLov: The Theory of Pl ast i ci t y which t akes
i nt o account Resi dual Microstresses. Appl. Math. Mech. 22, 104 (1959).
[13] EISENBE~G, M. A. , ~nd A. Pn~nr ~s: On Nonlinear Ki nemat i c Hardening. Act s Mech.
5, 1 (1968).
[14] G~EE~, A. E., and P. M. N A General Theory of an El ast i c-Pl ast i c Continuum.
Arch. Rat . Mech. Anal. 18, 251 (1965).
[15] KO~TEa, W. T. : St ress-St rai n RelatiOns, Uniqueness and Vari at i onal Theorems for
El ast i c-Pl ast i c Materials wi t h a Singular Yield Surface. Quart. Appl. Math. 11, 350
(1953).
[16] BATDFORD, S. B., and B. BUDI~s~:Y: A Mat hemat i cal Theory of Pl ast i ci t y Based on
t he Concept of Slip. TN 1871, NACA, 1949.
[17] I w~ , W. D. : On a Class of Models for t he Yielding Behavior of Continuous and Com-
posite Systems. J. Appl. Mech. 34, 612 (1967).
[18] M~oz, Z. : On t he Description of Anisotropie Workhardening. J. Mech. Phys. Solids 15,
163 (1967).
[19] M~oz, Z. : An At t empt to Describe t he Behavior of Metals under Cyclic Loads Using
a More General Workh~rdening Model. Act s Mech. 7, 199 (1969).
[20] Pm~u2s , A., and TA:~o Jv~-LI~r The Effect of Loading Pat h on t he Yield Surface
at El evat ed Temperatures. I nt , J. Solids St ruct ures 8, 463 (1972).
[21] I nt er nal Fri ct i on, Dampi ng and Cyclic Pl ast i ci t y. ASTM Special Technical Publ i cat i on
No. 378, aft er J o~) E~ Mo ~o w, p. 49, 1964.
[22] S~N~o~, B. I . : Fundament al s of Cyclic Stress and St rai n, 1st pri nt i ng, p. 30, 98. Uni-
versi t y of Wisconsin Press. 1972.
Yannis F. Da/alias and Pro/. Egor P. Popov
Division o/Structural Engineering
and Structural Mechanics
University o~ Cali]ornia
Berkeley, CA 9g 720, U.S.A.