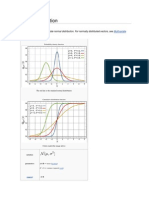
Ratio distribution

A ratio distribution (or quotient distribution) is a

probability distribution constructed as the distribution of
the ratio of random variables having two other known distributions. Given two (usually independent) random variables X and Y, the distribution of the random variable Z
that is formed as the ratio

distribution: The product and the ratio of two independent Cauchy distributions (with the same scale parameter and the location parameter set to zero) will give the
same distribution.[8] This becomes evident when regarding the Cauchy distribution as itself a ratio distribution of
two Gaussian distributions: Consider two Cauchy random
variables, C1 and C2 each constructed from two Gaussian
distributions C1 = G1 /G2 and C2 = G3 /G4 then

Z = X/Y
C1
G1 /G2
G1 G4
G1
G4
=
=
=

= C1 C3 ,
C2
G3 /G4
G2 G3
G2
G3

is a ratio distribution.
The Cauchy distribution is an example of a ratio distribution. The random variable associated with this distribution comes about as the ratio of two Gaussian (normal)
distributed variables with zero mean. Thus the Cauchy
distribution is also called the normal ratio distribution.
A number of researchers have considered more general
ratio distributions.[1][2][3][4][5][6][7][8][9] Two distributions
often used in test-statistics, the t-distribution and the Fdistribution, are also ratio distributions: The t-distributed
random variable is the ratio of a Gaussian random variable divided by an independent chi-distributed random
variable (i.e., the square root of a chi-squared distribution), while the F-distributed random variable is the ratio
of two independent chi-squared distributed random variables.

where C3 = G4 /G3 . The rst term is the ratio of two

Cauchy distributions while the last term is the product of
two such distributions.

2 Derivation
A way of deriving the ratio distribution of Z from the joint
distribution of the two other random variables, X and Y,
is by integration of the following form[3]

|y| pX,Y (zy, y) dy.

Often the ratio distributions are heavy-tailed, and it may

be dicult to work with such distributions and develop an
This is not always straightforward.
associated statistical test. A method based on the median
The Mellin transform has also been suggested for derivahas been suggested as a work-around.[10]
tion of ratio distributions.[8]

pZ (z) =

Algebra of random variables

3 Gaussian ratio distribution

Main article: Algebra of random variables

When X and Y are independent and have a Gaussian distribution with zero mean the form of their ratio distribution is fairly simple: It is a Cauchy distribution. However,
when the two distributions have non-zero means then the
form for the distribution of the ratio is much more complicated. In 1969 David Hinkley found a form for this
distribution.[6] In the absence of correlation (cor(X,Y) =
0), the probability density function of the two normal
variable X = N(X, X2 ) and Y = N(Y, Y 2 ) ratio Z
= X/Y is given by the following expression:

The ratio is one type of algebra for random variables: Related to the ratio distribution are the product distribution,
sum distribution and dierence distribution. More generally, one may talk of combinations of sums, dierences,
products and ratios. Many of these distributions are described in Melvin D. Springer's book from 1979 The Algebra of Random Variables.[8]

The algebraic rules known with ordinary numbers do not

apply for the algebra of random variables. For example,
if a product is C = AB and a ratio is D=C/A it does not
[ (
)
(
)]
1
b(z)
b(z)
1
b(z) d(z)
necessarily mean that the distributions of D and B are the

+ 2
pZ (z) =
same. Indeed, a peculiar eect is seen for the Cauchy
a3 (z)
a(z)
a(z)
a
(z)

2x y
1

5 CAUCHY RATIO DISTRIBUTION

4 Uniform ratio distribution

where

a(z) =
b(z) =
c=

1 2
1
z + 2
x2
y

x
y
z+ 2
x2
y

2y
2x
+
x2
y2

d(z) = e

With two independent random variables following a

uniform distribution, e.g.,
{
pX (x) =

1
0

0<x<1
otherwise

the ratio distribution becomes

b2 (z)ca2 (z)
2a2 (z)

1/2

0<z<1
z1
otherwise

And is the cumulative distribution function of the NorpZ (z) = 2z12

mal distribution

(t) =

1 2
1
e 2 u du
2

5 Cauchy ratio distribution

The above expression becomes even more complicated if

the variables X and Y are correlated. It can also be shown If two independent random variables, X and Y each folthat p(z) is a standard Cauchy distribution if X = Y = low a Cauchy distribution with median equal to zero and
shape factor a
0, and X = Y = 1. In such case b(z) = 0, and

p(z) =

1 1
1 + z2

pX (x|a) =

(a2

a
+ x2 )

If X = 1 , Y = 1 or = 0 the more general Cauchy then the ratio distribution for the random variable Z =
X/Y is [11]
distribution is obtained

pZ (z) =

,
(z )2 + 2

pZ (z|a) =

1
2 (z 2

1)

( )
ln z 2 .

where is the correlation coecient between X and Y This distribution does not depend on a and the result
stated by Springer [8] (p158 Question 4.6) is not correct.
and
The ratio distribution is similar to but not the same as the
product distribution of the random variable W = XY :
x
= ,
( 2)
y
a2
w
[8]
p
(w|a)
=
ln
2
2
4
W
(w a )
a4 .
x
=
1 2 .
y
More generally, if two independent random variables X
The complex distribution has also been expressed with and Y each follow a Cauchy distribution with median
Kummers conuent hypergeometric function or the equal to zero and shape factor a and b respectively, then:
Hermite function.[9]
1. The ratio distribution for the random variable Z =
X/Y is [11]

3.1

A transformation to Gaussianity

( 2 2)
ab
b z
A transformation has been suggested so that, under cer- p (z|a, b) =
ln
.
Z
2
2
2
2
(b z a )
a2
tain assumptions, the transformed variable T would approximately have a standard Gaussian distribution:[1]
2. The product distribution for the random variable W =
XY is [11]
y z x
t=
( 2 )
y2 z 2 2x y z + x2
w
ab
ln
.
pW (w|a, b) = 2 2
2
2
(w a b )
a2 b2
The transformation has been called the GearyHinkley
transformation,[7] and the approximation is good if Y is The result for the ratio distribution can be obtained from
unlikely to assume negative values.
the product distribution by replacing b with 1b .

Ratio of standard normal to stan- 9 See also

dard uniform

Inverse distribution
Product distribution

Main article: Slash distribution

If X has a standard normal distribution and Y has a standard uniform distribution, then Z = X / Y has a distribution known as the slash distribution, with probability
density function
{
pZ (z) =

[(0) (z)] /z 2
(0)/2

z=
0
z = 0,

where (z) is the probability density function of the standard normal distribution.[12]

Other ratio distributions

Let X be a normal(0,1) distribution, Y and Z be a chi

square distributions with m and n degrees of freedom respectively. Then

= tm
Y /m
Y /m
= Fm,n
Z/n
Y
= (m/2, n/2)
Y +Z
where t is Students t distribution, F is the F distribution
and is the beta distribution.

Ratio distributions in multivariate analysis

Ratio distributions also appear in multivariate analysis. If

the random matrices X and Y follow a Wishart distribution then the ratio of the determinants

= |X|/|Y|
is proportional to the product of independent F random
variables. In the case where X and Y are from independent standardized Wishart distributions then the ratio

= |X|/|X + Y|
has a Wilks lambda distribution.

Ratio estimator
Slash distribution

10 References
[1] Geary, R. C. (1930). The Frequency Distribution
of the Quotient of Two Normal Variates. Journal
of the Royal Statistical Society 93 (3): 442446.
doi:10.2307/2342070. JSTOR 2342070.
[2] Fieller, E. C. (November 1932). The Distribution of
the Index in a Normal Bivariate Population. Biometrika
24 (3/4): 428440. doi:10.2307/2331976. JSTOR
2331976.
[3] Curtiss, J. H. (December 1941). On the Distribution of the Quotient of Two Chance Variables. The
Annals of Mathematical Statistics 12 (4): 409421.
doi:10.1214/aoms/1177731679. JSTOR 2235953.
[4] George Marsaglia (April 1964). Ratios of Normal Variables and Ratios of Sums of Uniform Variables. Defense
Technical Information Center.
[5] Marsaglia, George (March 1965). Ratios of Normal
Variables and Ratios of Sums of Uniform Variables.
Journal of the American Statistical Association 60 (309):
193204. doi:10.2307/2283145. JSTOR 2283145.
[6] Hinkley, D. V. (December 1969). On the Ratio of Two
Correlated Normal Random Variables. Biometrika 56
(3): 635639. doi:10.2307/2334671. JSTOR 2334671.
[7] Hayya, Jack; Armstrong, Donald; Gressis, Nicolas (July
1975). A Note on the Ratio of Two Normally Distributed Variables. Management Science 21 (11): 1338
1341. doi:10.1287/mnsc.21.11.1338. JSTOR 2629897.
[8] Springer, Melvin Dale (1979). The Algebra of Random
Variables. Wiley. ISBN 0-471-01406-0.
[9] Pham-Gia, T.; Turkkan, N.; Marchand, E. (2006). Density of the Ratio of Two Normal Random Variables
and Applications. Communications in Statistics - Theory and Methods (Taylor & Francis) 35 (9): 15691591.
doi:10.1080/03610920600683689.
[10] Brody, James P.; Williams, Brian A.; Wold, Barbara
J.; Quake, Stephen R. (October 2002). Signicance
and statistical errors in the analysis of DNA microarray data. Proc Natl Acad Sci U S A 99 (20): 12975
12978. doi:10.1073/pnas.162468199. PMC 130571.
PMID 12235357.
[11] Kermond, John (2010). An Introduction to the Algebra
of Random Variables. Mathematical Association of Victoria 47th Annual Conference Proceedings - New Curriculum. New Opportunities (The Mathematical Association
of Victoria): 116. ISBN 978-1-876949-50-1.

11

[12] SLAPPF. Statistical Engineering Division, National Institute of Science and Technology. Retrieved 2009-0702.

11

External links

Ratio Distribution at MathWorld

Normal Ratio Distribution at MathWorld
Ratio Distributions at MathPages

EXTERNAL LINKS

12
12.1

Text and image sources, contributors, and licenses

Text

Ratio distribution Source: http://en.wikipedia.org/wiki/Ratio%20distribution?oldid=645064253 Contributors: Zundark, Fnielsen,

Michael Hardy, BenFrantzDale, Jason Quinn, Oliver Jennrich, Btyner, Rjwilmsi, Necrofear, Squidonius, InTheZone, DavidCBryant, DrMicro, HuMcCulloch, Melcombe, Oxnard28, Sun Creator, Qwfp, DOI bot, Dawynn, Jncraton, Yobot, AnomieBOT, LilHelpa, Citation
bot 1, Duoduoduo, RjwilmsiBot, Alanyiu, AaronMSwan, Dr Incredible, Illia Connell, Monkbot and Anonymous: 21

12.2

Images

12.3

Content license

Creative Commons Attribution-Share Alike 3.0