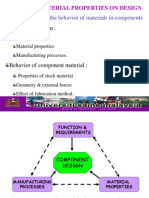
Peter Smith & Mike Rosenman

The size and shape of the crosssection of the piece of material

used

For timber, usually a rectangle

For steel, various formed

sections are more efficient

For concrete, either rectangular,

or often a Tee
A timber and plywood I-beam

University of Sydney Structures

SECTIONS

1/28

Peter Smith & Mike Rosenman

What shapes are

possible in the
material?

What shapes are

efficient for the
purpose?

Obviously, bigger
is stronger, but less
economical

University of Sydney Structures

Some hot-rolled steel sections

SECTIONS

2/28

Peter Smith & Mike Rosenman

Beams are oriented one way

Depth around the X-axis is the strong way

Some lateral stiffness is also needed

Columns need to be stiff both ways (X and Y)

Y
X

Timber
beam

Cold-formed Timber
steel
post

University of Sydney Structures

Hot-rolled
steel

Y
Steel
tube
SECTIONS

3/28

Peter Smith & Mike Rosenman

Stress is proportional to strain

Parts further from the centre strain more

The outer layers receive greatest stress

Unchanged length

Most shortened

Most lengthened
University of Sydney Structures

SECTIONS

4/28

Peter Smith & Mike Rosenman

The stresses developed resist bending

Equilibrium happens when the resistance equals

the applied bending moment
All the compressive
stresses add up to form a
compressive force C

a
T

MR = Ca
= Ta

Internal
Moment of
Resistance

All the tensile stresses add

up to form a tensile force T
University of Sydney Structures

SECTIONS

5/28

Peter Smith & Mike Rosenman

Simple solutions for rectangular sections

b

Doing the maths (in the Notes)

gives the Moment of Inertia
d

For a rectangular section

3
bd
I=
12
University of Sydney Structures

mm4

SECTIONS

6/28

Peter Smith & Mike Rosenman

The bigger the Moment of Inertia, the stiffer the

section

It is also called Second Moment of Area

Contains d3, so depth is important

The bigger the Modulus of Elasticity of the

material, the stiffer the section

A stiffer section develops its Moment of

Resistance with less curvature

University of Sydney Structures

SECTIONS

7/28

Peter Smith & Mike Rosenman

Simple solutions for rectangular sections

b

Doing the maths (in the Notes)

gives the Section Modulus
d

For a rectangular section

bd
Z=
6
University of Sydney Structures

2
mm3

SECTIONS

8/28

Peter Smith & Mike Rosenman

The bigger the Section Modulus, the

stronger the section

Contains d2, so depth is important

University of Sydney Structures

SECTIONS

9/28

Peter Smith & Mike Rosenman

Strength --> Failure of Element

Stiffness --> Amount of Deflection

depth is important

University of Sydney Structures

SECTIONS

10/28

Peter Smith & Mike Rosenman

The area tells how much stuff there is

used for columns and ties
directly affects weight and
cost

A = bd

The radius of gyration is a derivative of I

Y
b

used in slenderness ratio

rx = d/12
ry = b/12

Y
University of Sydney Structures

SECTIONS

11/28

Peter Smith & Mike Rosenman

Can be calculated, with a little extra work

Manufacturers publish tables of properties

University of Sydney Structures

SECTIONS 12/28

Peter Smith & Mike Rosenman

University of Sydney Structures

SECTIONS 12/28

Peter Smith & Mike Rosenman

Checking Beams
given the beam section
check that the stresses & deflection
are within the allowable limits

Designing Beams
find the Bending Moment and Shear
Force
select a suitable section

University of Sydney Structures

SECTIONS 13/28

Peter Smith & Mike Rosenman

Go back to the bending moment diagrams

Maximum stress occurs where bending moment is

a maximum
M is maximum here

Bending Moment
Stress =
Section Modulus
University of Sydney Structures

M
f=
Z
SECTIONS 14/28

Peter Smith & Mike Rosenman

b
d

Given the beam size and material

Find the maximum Bending Moment

Use Stress = Moment/Section Modulus

Compare this stress to the Code allowable stress

M = max BM
Z = bd2 / 6
Actual Stress = M / Z
Allowable Stress (from Code)

Actual < Allowable?

University of Sydney Structures

SECTIONS 15/28

Peter Smith & Mike Rosenman

Given a softwood timber beam 250 x 50mm

Given maximum Bending Moment = 4kNm

Given Code allowable stress = 8MPa

250

50

4 kNm

Section Modulus Z = bd2 / 6

= 50 x 2502 / 6
= 0.52 x 106 mm3
Actual Stress

f=M/Z
= 4 x 103 x 103 / 0.52 x 106
= 7.69 MPa < 8MPa

Actual Stress < Allowable Stress

University of Sydney Structures

SECTIONS 16/28

Peter Smith & Mike Rosenman

Given the maximum Bending Moment

Given the Code allowable stress for the material
Use Section Modulus = Moment / Stress
Look up a table to find a suitable section
M = max BM
Allowable Stress (from Code)

b?

required Z = M / Allowable Stress

a) choose b and d to give
Z >= than required Z or

d?

b) look up Tables of Properties

University of Sydney Structures

SECTIONS 17/28

Peter Smith & Mike Rosenman

Given the maximum Bending Moment = 4 kNm

b?
Given the Code allowable stress for
structural steel = 165 MPa
d?
required Z = 4 x 106 / 165 = 24 x 103 mm3
(steel handbooks give Z values in 103 mm3)
looking up a catalogue of steel purlins we find
C15020 - C-section 150 deep, 2.0mm thickness has a
Z = 27.89 x 103 mm3

University of Sydney Structures

(smallest section Z >= reqd Z)

SECTIONS 18/28

Peter Smith & Mike Rosenman

Both E and I come into the deflection formula

(Material and Section properties)

The load, W, and span, L3

Note that I has a d3 factor

Span-to-depth ratios (L/d) are often used

as a guide
W
Depth, d
Span, L

University of Sydney Structures

SECTIONS 19/28

Peter Smith & Mike Rosenman

Central point load

8d

Total load = W
(w per metre length)
L

5d

where W is the TOTAL load

University of Sydney Structures

WL
=
48 EI
Uniformly Distributed Load

5WL
=
384 EI
SECTIONS 20/28

Peter Smith & Mike Rosenman

Central point load

128d

Total load = W
(w per metre length)

WL
=
3EI

Uniformly Distributed Load

48d

L
where W is the TOTAL load
University of Sydney Structures

WL
=
8 EI

SECTIONS 21/28

Peter Smith & Mike Rosenman

Uniformly Distributed Load

Total load = W
(w per metre length)
L

WL
=
384 EI
where W is the TOTAL load

The deflection is only one-fifth of a

simply supported beam
Continuous beams are generally stiffer than
simply supported beam

University of Sydney Structures

SECTIONS 22/28

Peter Smith & Mike Rosenman

Given the beam size and material

Given the loading conditions

Use formula for maximum deflection

Compare this deflection to the Code allowable

deflection

Given load, W, and span, L

Given Modulus of Elasticity, E, and Moment of Inertia, I
Use deflection formula to find deflection
Be careful with units (work in N and mm)
Compare to Code limit (usually given as L/500, L/250 etc)
University of Sydney Structures

SECTIONS 23/28

Peter Smith & Mike Rosenman

W = 8kN

Check the deflection of the steel channel

previously designed for strength
The maximum deflection <= L / 500
Section = C15020

E = 200 000 MPa

= (5/384) x WL3/EI mm

L = 4m
Loading Diagram

I = 2.119 x 106 mm4

( Let us work in N and mm )

= (5/384) x 8000 x 40003 / (200000 x 2.119 x 106)

= 16 mm

Maximum allowable deflection = 4000 / 500

= 8 mm

deflects too much - need to chose stiffer section

University of Sydney Structures

SECTIONS 24/28

Peter Smith & Mike Rosenman

65

Need twice as much I

150

Could use same section back to back

100% more material
75

A channel C20020 (200 deep 2mm thick)

has twice the I but only 27% more material

200

design for strength

check for deflection
strategy for heavily loaded beams
University of Sydney Structures

SECTIONS 25/28

Peter Smith & Mike Rosenman

Given the loading conditions

Given the Code allowable deflection

Use deflection formula to find I

Look up a table to find a suitable section

Given load, W, span, L, and Modulus of Elasticity, E

Use the Code limit e.g., turn L/500 into millimetres
Use deflection formula to find minimum value of I
Look up tables or use I = bd3/12 and choose b and d
University of Sydney Structures

SECTIONS 26/28

Peter Smith & Mike Rosenman

= better sections for beams

Beams need large I and Z in direction of bending

Need stiffness in other direction to resist

lateral buckling

Columns usually need large value of r

in both directions
Some sections useful for both

University of Sydney Structures

SECTIONS 27/28

Peter Smith & Mike Rosenman

Deep beams are economical but subject to

lateral buckling

University of Sydney Structures

SECTIONS 28/28