1

Year 9: Sequences
Ex 1.1. What is the next number in the following sequence?
10, 100, 1000, 10 000, ...

Ex 1.2. What is the next number in this sequence?

1, 2, 4, 7, 11, 16,

Ex 1.3. Write down the first four terms of the sequence

whose nth term is given by T(n) = 4n + 2.

Ex 1.4. Write down the nth term of the sequence 2, 5, 8, 11,

.

Ex 1.5. Write down the nth term of the sequence 5, 9, 13, 17,
21, .

Exercise 1A

1. Find the next three terms in each of the following

sequences.
a. 1, 5, 9, 13,
b. 3, 8, 13, 18,
c. 2, 9, 16, 23,
d. 4, 10, 17, 25,
e. 6, 14, 24, 36,
f. 5, 8, 13, 20,
2. Write down the first four terms of each of the following
sequences whose nth term is given below.
a. 2n + 3

b. 3n 2

c. 4n + 5

d. 5n 3

e. 3n 1

f. 4n 5

g. 2n 4

3. Find the nth term of each of the following sequences.

a 6, 10, 14, 18, 22,
36,

b 8, 15, 22, 29,

c 21, 19, 17, 15, 13,

16,

d 32, 28, 24, 20,

4. Find the nth term of each of the following sequences.

a 43, 51, 59, 67, 75,

b 57, 50, 43, 36, 29,

c 35, 48, 61, 74, 87,

d 67, 76, 85, 94, 103,

5. Find the nth term of each of the following sequences.

a 9, 4, 1, 6, 11,

b 11, 9, 7, 5, 3,

c 1, 5, 9, 13, 17,

d 15, 12, 9, 6, 3,

6. Find the nth term of each of the following sequences.

a 2.4, 2.6, 2.8, 3.0, 3.2,

2.9,

b 1.7, 2.0, 2.3, 2.6,

c 6.8, 6.3, 5.8, 5.3, 4.8,

3.7,

d 5.3, 4.9, 4.5, 4.1,

7. Find the nth term of each of the following sequences of

fractions.
a

1 2 3 4 5
, , , , ,
2 5 8 11 14

3 5 7 9 11
, , , , ,
4 9 14 19 24

8. Look at each of the following sequences of squares.

a. Find the number of squares in the nth shape.

b. Find the number of squares in the 50th shape in the

pattern.

9. Look at each of the following sequences of lines (blue) and

crosses (green).

a Find the number of lines in the nth shape.

b Find the number of crosses in the 50th shape in the pattern.
c Find the number of crosses in the nth shape in the pattern.
Extension work:
The nth term of a sequence is given by

1
n(n+1).
2

1. Work out the first five terms of the sequence.

2. Write down the term-to-term rule for the sequence.

3. Continue the sequence for 10 terms.

4. What special name is given to this sequence of numbers?

Quadratic sequences

You have already met the sequence of square numbers: 1,

4, 9, 16, 25, 36,
The nth term of this sequence is n2.
Many sequences have nth terms that include n2.These are
called quadratic sequences.
Ex 1.6. The nth term of a quadratic sequence is given by n2
+ 3n + 2.
a. Work out the first five terms of the sequence.

b. Write down the term-to-term rule for this sequence.

c. Continue the sequence for ten terms.

d. What is the 100th term in the sequence?

Ex. 1.7. Write down the nth term of the following sequences.
a 1, 4, 9, 16, 25,
27,

c 2, 8, 18, 32, 50,

b 3, 6, 11, 18,

1
1
1
, 2, 4 , 8,12 ,
2
2
2

Exercise 1B
1. Write down the first four terms of each of the following
sequences whose nth term is given below.
a. n2

b. n2 + 1

c. n2 + n

d. n2 + 3n + 4

2. For each of the following nth terms:

i work out the first five terms of the sequence.
down the term-to-term rule for this sequence.

ii write

iii continue the sequence for ten terms.

a. n(n + 3)

c. n2 + 5

e. (n + 3)(n 2)

b. 3n2

d. (n + 1)2

f. 2n2 + n + 1

3. Write down the nth term of the following sequences.

a 1, 4, 9, 16, 25,
26,

c 5, 20, 45, 80, 125,

b 2, 5, 10, 17,

d , 1, 2 , 4, 6 ,

4. Look at the way straight lines can intersect one another.

The maximum number of intersections for each set of lines is

shown in the table below.
Number of lines
1
2
3
4
Maximum number of intersections
0
1
3
6
a. Before drawing a diagram, can you predict, from the table,
the maximum number of intersections you will have for five
lines? Draw the five lines so that they all intersect one
another. Count the number of intersections. Were you right?

b. Now predict the maximum number of intersections for six

and seven lines. Draw the diagram for six lines to confirm
your result.

c. Which of the following is the nth term of the sequence?

1
2

n(n + 1)

1
2

(n 1)(n + 1)

n(n 1)
5. Look at the following polygons. Each vertex is joined to
every other vertex with a straight line, called a diagonal.

The table below shows the number of diagonals drawn inside

each polygon.
Number of sides

Number of diagonals

14

a. Before drawing a diagram, can you predict, from the table,

the number of diagonals you will have for a polygon with
eight sides?
b. Draw an eight-sided polygon and put in all the diagonals.
Count the number of diagonals. Were you right?

c. Now predict the number of diagonals for polygons with

nine and ten sides.
d. Check your results for part c by drawing the polygons with
their diagonals and seeing how many diagonals there are in
each case.

10

e. Which of the following is the nth term of the sequence?

1
2

(n + 2)(n 1)

1
2

n +n1
2

1
2

(n2

+ n 2)
6. Write down the first five terms of each of the following
sequences.
a. T(n) = (n + 1)(n + 2)
(n 2)

b. T(n) = (n 1)

c. T(n) = n + (n 1)(n 2)
1)(n 2) (n 3)

d. T(n) = 2n + (n

e. T(n) = 3n + (n 1)(n 2)(n 3)(n 4)

11

Extension Work
What is the pattern of second differences in T(n) = n2?
The first six terms of the sequence T(n) = n2, where T(1) = 1,
are: 1, 4, 9, 16, 25, 36
The first differences are those between consecutive terms.
These are:
1
4
9
16 25 36
3
5
7
9
11
The second differences are those between consecutive first
differences, as shown below:
3
5
7
9
11
2
2
2
2
Every quadratic sequence has second differences which are
the same throughout the sequence, as shown above.
1
a. Find the second differences for each of the following
sequences by writing down the first six terms.
i T(n) = n2 + 3n + 4
ii T(n) = n2 + 4n
+3

b. What do you notice about each second difference?

12

2
a. Find the second differences for each of the following
sequences by writing down the first six terms.
i T(n) = 2n2 + 3n + 4
ii T(n) = 2n2 +
4n + 3

b. What do you notice about each second difference?

c. What do you expect the second difference to be for

T(n) = 3n2 + 3n + 4?

13

Functions
A function is a rule which changes one number, called the
input, to another number, called the output. For example,
y = 2x + 1 is a function. So, when x = 2, a new number y =
5 is produced. Another way of writing this function is:
x 2x + 1

Identity function
x x is called the identity function because it maps any
number onto itself. In other words, it leaves the inputs
unaltered.
00

11
44

22

33

Inverse function
Every linear function has an inverse function which reverses
the direction of the operation. In other words, the output is
brought back to the input.
Ex 1.8. The inverse function of x 4x is seen to be

y
.
4

Ex 1.9. The inverse function of x x + 3 is seen to be y y

3.

14

When a function is built up from two or more operations, you

will need to consider the original operations and work
backwards through these to find the inverse.
Ex 1.10. Find the inverse function of x 4x + 3.
The sequence of operations for this function is :
Reversing this sequence gives:
The give the output the value y:
So the inverse function is:

Self-inverse function
The inverse functions of some functions are the functions
themselves. These are called self-inverse functions.
Ex 1.11. The inverse function of x 8 x can be seen to be
itself as y 8 y.

Exercise 1C
1. Write down the inverse function of each of the following
functions.
a . x 2 x b . x 5 x c . x x+6

d . x x +1 e . x x 3 f . x

x
5

15

2. For each of the following functions:

i draw the flow diagram for the function.
ii draw the flow diagram for the inverse function.
iii write down the inverse function in the form y
a. x 2x + 3

b. x 3x +

c. x 4x 3

e. x 4x + 7

d. x 5x 2

f. x 6x 5

3. Show that the following are self-inverse functions.

a. x 6 x

b. x 2/x

4. Write down the inverse function of each of the following

functions.

16

a. x 2(x + 3)

b. x 3(x 4)

c.

x+3
4

d.

( x2 )
5

e.

1
x x +3
2

f.

1
x x7
2

Extension work
1 The function x 2x can also be expressed as y = 2x. Show
this to be true by considering the input set {1, 2, 3, 4, 5}.
a. What is the output set from {1, 2, 3, 4, 5} with the
function x 2x?

b. Find the values of y when x has values {1, 2, 3, 4, 5},

where y = 2x.

c. Are the two sets of values found in parts a and b the same?
If so, then you have shown that y = 2x is just another way of
showing the function x 2x.

17

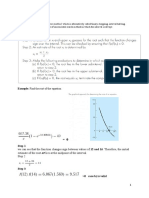
2. Draw a graph of the function x 2x by using y = 2x. On

the same pair of axes, draw the graph of the inverse function
of x 2x.

3. On the same pair of axes, draw the graphs representing

the function x 4x and its inverse function.

4. On the same pair of axes, draw the graphs representing

the function x 5x and its inverse function.

5. Look at the two lines on each graph you have drawn for
Questions 2, 3 and 4. Do you notice anything special about
each pair of lines?