Académique Documents
Professionnel Documents
Culture Documents
3 Kinematics
Transféré par
joeTitre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
3 Kinematics
Transféré par
joeDroits d'auteur :
Formats disponibles
1
KINEMATICS (motion of objects without reference to the forces that cause the motion)
Distance: is the total length covered irrespective of direction of motion
Displacement (x, d, s): is the linear distance in a given direction from a reference point.
Speed: is the rate of change of distance travelled
Velocity (u or v): is the rate of change of displacement
Acceleration (a): is the rate of change of velocity
DISPLACEMENT-TIME (
) GRAPH
s
On s-t graph, gradient of s-t graph = (instantaneous) velocity
s1
C
B
A
t
J
-s2
At A: stationary, A-B: accelerating (slope increasing), B-C: moving with constant velocity
(slope constant), C-D: decelerating (slope decreasing), D-E: stationary
E-F: accelerating and moving back towards the starting point, F-G: moving with constant
velocity, At G momentarily at the starting point,
G-H: moving away from the starting point with constant velocity in the opposite direction to the
original direction, H-I: decelerating, At I momentarily stationary, I-J: accelerating and moving
back towards the starting point, J-K: decelerating, At K: stationary at the starting point.
At the end of the period under consideration the engine is back at its starting point and therefore
has zero displacement; the distance it has travelled, however, is 2s 1+2s2
Average velocity =
Uniform velocity means displacement changes by equal amounts in equal intervals of time
Instantaneous velocity =
or
in calculus notation
VELOCITY-TIME (
) GRAPH
On v-t graph, gradient of v-t graph = acceleration
area under v-t graph = change in displacement
v
C
A1
E
0 A
A2
G
A-B: moves from rest with a constant acceleration
B-C: velocity still increasing, acceleration decreasing
C-D: moving with constant velocity
D-E: decelerating at a constant rate. Comes to rest.
E-F: stationary
F-G: moving in the opposite direction to the original direction. Acceleration constant.
G-H: constant velocity
H-I: decelerating at a constant rate. Comes to rest
Total distance moved = A1 +A2. Net distance moved (e.g magnitude of displacement =A1-A2)
Note: (i)
(ii) Instantaneous acceleration at time t
gradient of tangent to curve at time t
rise
Acceleration of free fall ( )
In free fall condition, only gravity acts and there is no air resistance.
Close to Earths surface, any object has an acceleration of g = 9.81 ms-2
fall
a=g
a=-g
gravity
GRAPHICAL REPRESENTATION OF MOTION
e.g 1: Ball thrown upwards at velocity v:
max. point
speed
velocity
+ v-
R
v
R t2
t1
-v
Take upwards
+,
R = height ball
rises,
t1 = time taken
to reach
maximum
point,
t2 = 2t1 = time
taken to return
to starting point
time
distance
displacement
t1
time
t2
2R
t1
t2
time
e.g 2: Ball released from rest and bounced off the ground:
Take downwards +
t1
t2
v
v1
h0
h0
v2
h1
h1
-v2
v1
displacement
H
s
y
H
y
time
time
e.g 3: Ball bounces off the ground several times:
A ball is released from rest above a horizontal rigid
surface and bounces off several times. Sketch a
graph to show (i) how the velocity v of the ball
varies with time t, (ii) how the displacement s of the
ball from the point of release varies with time t, (iii)
how the acceleration a of the ball varies with time t.
ground
Level
Because of loss of energy v1 > v2 > v3 >
v4
s1 = displacement measure from point of release
s2 = displacement measure from ground level
Take downwards +
Explaining the spike in a-t graph:
When the ball is in the air (either moving up or
down), the only force acting on the ball is weight
(downwards). Since F = ma, the direction of
acceleration is the same as the direction of the net
force acting on the ball (downwards), hence
positive at 9.81 ms-2.
At the instant when the ball collide with the ground,
there is an additional normal contact force on the
ball by the ground, hence the net force on ball is
upwards. Therefore acceleration is upwards,
which is negative as it is in the opposite direction of
the reference direction. Once the ball leaves the
ground, net force is weight downwards, hence is
positive again.
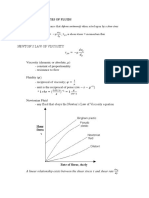
EQUATIONS OF MOTION FOR UNIFORMLY ACCELERATION MOTION IN A
STRAIGHT LINE
velocity
u = Initial velocity (velocity at time = 0)
v = final velocity (velocity at time t)
t = time taken
<v> = average velocity
s = displacement in time t
time
1.
derived from the definition of
2.
derived from s = area under v-t graph
3.
4.
derived from equations (1) and (2)
derived from equations (1) and (2) or (3)
Note: These equations apply only if the motion takes place along a straight line and the
acceleration is constant (e.g in the case where air resistance is neglected)
EXPERIMENT TO DETERMINE THE ACCELERATION OF FREE-FALL USING A
FALLING BODY
Steel ball is dropped from rest. The electronic timer starts when the ball is released by opening
switch and stops when it breaks the contact plates. The time t measured is the time the ball takes
to fall through h metres. From
,
Vary h and measure t. Plot a graph of h against t2.
Average value of g = 2 gradient
Electromagnet
ball
timer
contact
plates
MOTION DUE TO A UNIFORM VELOCITY IN ONE DIRECTION AND A UNIFORM
ACCELERATION IN A PERPENDICULAR DIRECTION - projectile motion
A body projected through a gravitational field will describe a projectile motion if only gravity
acts on it. In parabolic motion, the force acting on a body is constant in magnitude and direction.
There are three cases of projectile motion:
First case: projected vertically (horizontal velocity zero)
Take upward motion positive.
Vertical components
Horizontal components
ay = - g
vy = u-gt
sy = ut - gt2
ax= 0
vx = 0
sx = 0
Second case: A body projected horizontally with a constant velocity u (initial vertical
velocity zero)
Ignoring air resistance, the horizontal velocity component vx remains constant and its horizontal
acceleration component ax is zero as gravity acts vertically downwards. The vertical velocity
component vy which is initially zero increases at a rate of 9.8 ms -2. A stroboscope can picture the
path of the projectile at regular time interval t. This gives multiflash photographs.
2t
3t
x-axis
y-axis
vx
Take downwards positive.
Vertical components
Horizontal components
ay = g
vy = 0
ay = + g
v = u + at
vy = gt
s = ut + at2
sy = 0 + gt2
sy = gt2
ax = 0
vx = u
ax = 0
Initially (t = 0)
At time t
vx = u (constant)
sx = ut
Note: Only t is a scalar (no direction), i.e. common to both x- and y-directions.
Third case: A body projected with a velocity
at an angle to the horizontal
Velocity u is resolved into its two perpendicular components vx and vy.
vy
vx
usin
sy
ucos
-usin
t
vy
vx
sx
sy
sx
ax
ay
T = time of flight
R = range
H = maximum height
t
-g
t
Take upwards positive:
at all times
Initially, t = 0
At time = t
At maximum point/height
Along horizontal direction
Along vertical direction
ax= 0
vx= u (constant)
vx= ucos
vx= ucos
sx = (ucos)t
vx= ucos
ay = - g
vy varies by g
vy= usin
vy= usin-gt
sy = (usin)t - g t2
vy=0
Projectile motion with air resistance:
without air resistance
(parabola shape)
with
air resistance
Important note about Projectile:
(1) There is no need to remember the equations for H and R.
(2) All problems on projectile can be solved using the rectilinear equations.
(3) When using the rectilinear equations, take note of the direction.
Consider only one direction for any one equation.
(4) Time is the only quantity that is common for both x- and y- directions.
Vous aimerez peut-être aussi
- Measurement and Observations: Paper 4 - Alternative To Practical PaperDocument4 pagesMeasurement and Observations: Paper 4 - Alternative To Practical PaperjoePas encore d'évaluation
- Measurement and UncertaintiesDocument10 pagesMeasurement and UncertaintiesjoePas encore d'évaluation
- Sy F3Document2 pagesSy F3Michael LeungPas encore d'évaluation
- Httpminiphysics Blogspot ComDocument11 pagesHttpminiphysics Blogspot ComjoePas encore d'évaluation
- Student Results, G/ms A B C DDocument3 pagesStudent Results, G/ms A B C DjoePas encore d'évaluation
- Project Application Form FOR Rainwater Harvesting SchemeDocument7 pagesProject Application Form FOR Rainwater Harvesting SchemejoePas encore d'évaluation
- Phy9702 P5 Q2Document2 pagesPhy9702 P5 Q2joePas encore d'évaluation
- Newton's First LawDocument18 pagesNewton's First LawjoePas encore d'évaluation
- Wpe ExercisesDocument11 pagesWpe ExercisesjoePas encore d'évaluation
- Wpe ExercisesDocument11 pagesWpe ExercisesjoePas encore d'évaluation
- McqsDocument12 pagesMcqsjoePas encore d'évaluation
- List of Practicals 2016Document1 pageList of Practicals 2016joePas encore d'évaluation
- McqsDocument12 pagesMcqsjoePas encore d'évaluation
- ρ v k, where p is a pressure, h a height,Document2 pagesρ v k, where p is a pressure, h a height,joePas encore d'évaluation
- 10 Ideal GasesDocument7 pages10 Ideal GasesjoePas encore d'évaluation
- Questions on Fundamental Particles: Cs Cs Cs Cs β β β βDocument10 pagesQuestions on Fundamental Particles: Cs Cs Cs Cs β β β βjoePas encore d'évaluation
- Band Theory NotesDocument14 pagesBand Theory NotesjoePas encore d'évaluation
- FVT 2015Document9 pagesFVT 2015joePas encore d'évaluation
- Angular Displacement: Circular Motion Kinematics of Uniform Circular MotionDocument6 pagesAngular Displacement: Circular Motion Kinematics of Uniform Circular MotionjoePas encore d'évaluation
- Mark Scheme 2014Document4 pagesMark Scheme 2014joePas encore d'évaluation
- Additional Complex Number Problems PDFDocument2 pagesAdditional Complex Number Problems PDFvinod_eicsPas encore d'évaluation
- Physics For Importance of Natural ResourcesDocument12 pagesPhysics For Importance of Natural ResourcesjoePas encore d'évaluation
- Forces NotesDocument6 pagesForces NotesjoePas encore d'évaluation
- Doppler Effect: V Speed of Wave VDocument10 pagesDoppler Effect: V Speed of Wave Vjoe0% (1)
- 10 Ideal GasesDocument7 pages10 Ideal GasesjoePas encore d'évaluation
- TEST16 ADocument3 pagesTEST16 AjoePas encore d'évaluation
- Examination Structure: Assessment ObjectivesDocument2 pagesExamination Structure: Assessment ObjectivesjoePas encore d'évaluation
- Core Mathematics 4 Jun14Document4 pagesCore Mathematics 4 Jun14joePas encore d'évaluation
- Examination Techniques For GccceDocument1 pageExamination Techniques For GcccejoePas encore d'évaluation
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeD'EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeÉvaluation : 4 sur 5 étoiles4/5 (5794)
- Shoe Dog: A Memoir by the Creator of NikeD'EverandShoe Dog: A Memoir by the Creator of NikeÉvaluation : 4.5 sur 5 étoiles4.5/5 (537)
- The Yellow House: A Memoir (2019 National Book Award Winner)D'EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Évaluation : 4 sur 5 étoiles4/5 (98)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceD'EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceÉvaluation : 4 sur 5 étoiles4/5 (895)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersD'EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersÉvaluation : 4.5 sur 5 étoiles4.5/5 (344)
- The Little Book of Hygge: Danish Secrets to Happy LivingD'EverandThe Little Book of Hygge: Danish Secrets to Happy LivingÉvaluation : 3.5 sur 5 étoiles3.5/5 (399)
- Grit: The Power of Passion and PerseveranceD'EverandGrit: The Power of Passion and PerseveranceÉvaluation : 4 sur 5 étoiles4/5 (588)
- The Emperor of All Maladies: A Biography of CancerD'EverandThe Emperor of All Maladies: A Biography of CancerÉvaluation : 4.5 sur 5 étoiles4.5/5 (271)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaD'EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaÉvaluation : 4.5 sur 5 étoiles4.5/5 (266)
- Never Split the Difference: Negotiating As If Your Life Depended On ItD'EverandNever Split the Difference: Negotiating As If Your Life Depended On ItÉvaluation : 4.5 sur 5 étoiles4.5/5 (838)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryD'EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryÉvaluation : 3.5 sur 5 étoiles3.5/5 (231)
- On Fire: The (Burning) Case for a Green New DealD'EverandOn Fire: The (Burning) Case for a Green New DealÉvaluation : 4 sur 5 étoiles4/5 (73)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureD'EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureÉvaluation : 4.5 sur 5 étoiles4.5/5 (474)
- Team of Rivals: The Political Genius of Abraham LincolnD'EverandTeam of Rivals: The Political Genius of Abraham LincolnÉvaluation : 4.5 sur 5 étoiles4.5/5 (234)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyD'EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyÉvaluation : 3.5 sur 5 étoiles3.5/5 (2259)
- The Unwinding: An Inner History of the New AmericaD'EverandThe Unwinding: An Inner History of the New AmericaÉvaluation : 4 sur 5 étoiles4/5 (45)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreD'EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreÉvaluation : 4 sur 5 étoiles4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)D'EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Évaluation : 4.5 sur 5 étoiles4.5/5 (120)
- Her Body and Other Parties: StoriesD'EverandHer Body and Other Parties: StoriesÉvaluation : 4 sur 5 étoiles4/5 (821)
- Perturbation TheoryDocument4 pagesPerturbation Theoryapi-3759956100% (1)
- A Is Shear Stress Momentum FluxDocument21 pagesA Is Shear Stress Momentum FluxPamela MendozaPas encore d'évaluation
- Define An IndicatrixDocument4 pagesDefine An IndicatrixTYron AnotidaPas encore d'évaluation
- Quantum Optics Standing Wave Quantization: M. Brune, A. Aspect Homework of Lesson 1Document4 pagesQuantum Optics Standing Wave Quantization: M. Brune, A. Aspect Homework of Lesson 1bruhbruhbruh100% (2)
- Chemistry Periodic Table PPT 1Document17 pagesChemistry Periodic Table PPT 1Hazel ValenzuelaPas encore d'évaluation
- Casting DefectsDocument16 pagesCasting DefectsAshok PradhanPas encore d'évaluation
- Determination of Iron With 1,10-PhenanthrolineDocument5 pagesDetermination of Iron With 1,10-PhenanthrolineOmSilence26510% (1)
- Jee 2014 Booklet3 HWT Solutions Ionic EquilibriumDocument3 pagesJee 2014 Booklet3 HWT Solutions Ionic EquilibriumvarunkohliinPas encore d'évaluation
- Section 1.1: Motion and Motion GraphsDocument15 pagesSection 1.1: Motion and Motion GraphsMiranda M. Y. LeungPas encore d'évaluation
- DPP-1 To 8 - Modern Physics - JEEDocument54 pagesDPP-1 To 8 - Modern Physics - JEEKeerthana Reddy DomaPas encore d'évaluation
- Delia Schwartz-Perlov and Alexander Vilenkin - Measures For A Transdimensional MultiverseDocument30 pagesDelia Schwartz-Perlov and Alexander Vilenkin - Measures For A Transdimensional MultiverseDex30KMPas encore d'évaluation
- How Boomerangs WorkDocument9 pagesHow Boomerangs Workchey007Pas encore d'évaluation
- Rangkuman TRK (Deva Punya)Document4 pagesRangkuman TRK (Deva Punya)gamalielPas encore d'évaluation
- Reduction With Rieke ZincReduction With Rieke ZincDocument3 pagesReduction With Rieke ZincReduction With Rieke ZinciramshaguftaPas encore d'évaluation
- The Catenary PDFDocument5 pagesThe Catenary PDFChandra PrakashPas encore d'évaluation
- ch5 6 7Document1 pagech5 6 7Jeff MartinPas encore d'évaluation
- Physical Sciences Baseline Test Gr11Document7 pagesPhysical Sciences Baseline Test Gr11Midyondzi ngobeniPas encore d'évaluation
- Basic Electronics PracticalDocument9 pagesBasic Electronics Practicalasfadare100% (2)
- 40 Micellar CatalysisDocument4 pages40 Micellar CatalysisdarkknightonePas encore d'évaluation
- Total Length Calcs For Pipes Valves and Fittings RevADocument9 pagesTotal Length Calcs For Pipes Valves and Fittings RevAlutfi awnPas encore d'évaluation
- Chapter 1 PDFDocument14 pagesChapter 1 PDFNama Desalew100% (1)
- Space Physics NotesDocument30 pagesSpace Physics Notesfgthy100% (1)
- Steam - Basic Concepts &: FundamentalsDocument11 pagesSteam - Basic Concepts &: FundamentalsermiasPas encore d'évaluation
- Relative VelocityDocument7 pagesRelative VelocityJanaka Priyalal100% (3)
- Dark Energy DissertationDocument7 pagesDark Energy DissertationBestPaperWritingServiceUK100% (1)
- AEEE 2023 - Sample PapersDocument99 pagesAEEE 2023 - Sample Paperssri sai surajPas encore d'évaluation
- Ideal FluidDocument2 pagesIdeal FluidaathiraPas encore d'évaluation
- Review 3 SearchableDocument16 pagesReview 3 SearchablehquynhPas encore d'évaluation
- Class:12 Physics Assignment 8 Topic: Electromagnetic InductionDocument3 pagesClass:12 Physics Assignment 8 Topic: Electromagnetic InductionAkshat RawatPas encore d'évaluation
- Multiple ChoiceDocument61 pagesMultiple ChoiceDenaiya Watton Leeh100% (7)