1

Oscillations
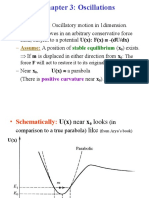
Chapter 14: Oscillations
Read Chapter 14 this week. We shall cover Sections 14.1, 2, 3 this week
Section 14.1, 2, 4 Simple Harmonic Motion
Consider a block (or air track glider) attached to a spring (horizontal) and on a
frictionless surface.
In equilibrium, with the spring relaxed, the block sits still
at a point we shall define as x=0, the equilibrium
position.

Frictionless surface.

If we move the block to the right a distance x, the spring

exerts a force, F, tending to pull the block back to the left
towards the equilibrium position.

F
0

x
F

The force exerted by the spring on the block is

F = -kx

If we move the block to the left a distance x, the spring

exerts a force, F, tending to push the block right towards
the equilibrium position.
The further we pull on the spring, the larger the
force we have to pull. For most springs, provided
we dont pull or push too hard, the restoring force is
proportional to the displacement from equilibrium.

(where x is the displacement from equilibrium)

where k is the force constant of the spring. Hookes Law. Units of k are N/m.
F = ma =md2x = -kx This is the equation of motion for the block-spring system
dt2
a = -(k/m)x
It is also the general equation for a system (Simple Harmonic Oscillator) undergoing
simple harmonic motion.
An object moves with simple harmonic motion whenever its restoring force is
proportional to its displacement from some equilibrium position and is oppositely
directed.

Solutions for the above Equation of motion: d2x = - (k/m) x

dt2
x = Acos(t + )

x
time
t=0
A

(take first derivative of x)

v = dx = -Asin(t + ) v
dt

t
2A

a = dv = -2Acos(t + ) a
dt

A sine wave is characterised by three quantities

1) Amplitude A
2) Angular frequency (radians/s) = 2f where f is in cycles/s or Hz
3) Phase (radians)
How many radians in 360o?
Period T = 1/f = 2/ = time for one full cycle of the motion. Note that T = 2 this is
the period over which a sine wave repeats itself.
Note (1): The displacement, velocity and acceleration of the block follow sine waves
which are of the same frequency but different phase.
Note (2): the amplitude and frequency of the motion are independent
For the spring- block problem (either horizontal or vertical)
d2x = -k/mx = -2x using the solutions above for SHM
dt2
So, 2 = k/m or T = 2(m/k)
the mass and the force constant)

(Note that the period of the motion depends only on

Problem #3 on previous P101 midterm. A Block Spring system is characterised by a

spring force constant of 50.0 N/m and a mass of 10.0 kg. At t=0, the block is given a
velocity of 1.00 m/s at its equilibrium position (x=0.000). Assuming no damping,
(a) How long does it take the block to first return to its initial position?
The spring returns to its initial position in T = 2(m/k)/2 = ([(10.0kg)/(50 N/m)] =
1.405s
x
t
(b) What is the maximum amplitude of oscillation of the block?
Note that the maximum
velocity occurs at t=0

= k/m = [(50.0 N/m)/(10.0kg)] =2.24 s-1

use vmax = A then A = vmax/ = vmax / (k/m) = (1.0m/s)*(10.0kg/50.0N/m) = 0.447m

(c) What is the equation of motion for the block? i.e. show the equation for the block
displacement as a function of time.
x = Acos(t + ) A = 0.447m, and Acos() = 0; = -/2, 3/2, 7/2, ...
Then x = (0.447m)cos(2.24t - /2)
Problem: A particle undergoing simple harmonic motion follows a trajectory (solid line)
as shown below.
10
5
x(cm)
2

t(s)

-5
-10
Find , v (0) and vmax
T = 8s, = 2/T = 0.785 s-1, A = 10 cm. x(0) = Acos = 5cm; = cos-1(0.5) = 1.02 rad
Note that cos () = cos (-) (and sin () = - sin(-)) If we use the x position at a single
time and the amplitude alone to determine phase, then we cannot distinguish between the

positive and the negative value for . The positive value for corresponds to the dotted
curve and the negative value for corresponds to the solid line. Therefore we choose the
negative value, -1.05 rad.
The v(0) = - Asin() = - 0.785s-1* 10cm*sin (-1.05rad) = 6.8 cm/s and vmax = A = 7.85
cm/s
Section 14.3: Energy in simple harmonic motion:
K = mv2 = m2A2sin2(t + ) = kA2sin2(t + ) using 2 = k/m

We neglect the mass of the

spring.

U = kx2 = kA2cos2(t + ) at any time (work in moving the mass (F = -kx a

distance x) U = -Fdx = kx2.
Then the total mechanical energy of the block-spring system is
E = K + U = kA2(sin2(t + ) + cos2(t + )) = kA2 using sin2 + cos2 = 1
The total mechanical energy of the simple harmonic oscillator is a constant of the
motion and is proportional to the square of the amplitude.
How does the energy change from kinetic to potential as the spring block system
undergoes SMH?
At the maximum extension and at the equilibrium point, what are the potential and
kinetic energies?
K=0; U= kA2; E = kA2
x = A, v = 0
K = mvmax2, U = 0; E = mvmax2
x=0, v = vmax

Intermediate position, x = x

E = mv2 + kx2 = kA2 =mvmax2

Now, we can solve for v as a function of x

mv2 + kx2 = kA2; v2 = k/m(A2 - x2); v = k/m(A2 - x2) or, since vmax= Ak/m
v = vmax (1 - x2/A2)

Problem: A 1.00kg block slides on a frictionless surface with a speed of 2.00 m/s. The
block meets an unstretched spring with force constant 250 N/m.
(a) How far is the spring compressed before the block comes to rest?
mv2 = kA2 ; then A = vm/k = 2.00m/s*1.00kg/250N/m = 0.126m =12.6cm.
The relevant time is T/2 because we
know the final velocity of the block
will be 2.00m/s and that will be the
velocity of the end of the spring after
T/2. From this point on the spring
slows down.

(b) How long is the block in contact with the spring?

Period of contact = T/2 where T=2m/k;
Period of contact = 1.00kg/250N/m) = 0.199s

Section 14.5 Vertical Oscillations

Consider a mass hanging from a vertical spring.
When the mass is attached to the spring, it extends a
distance L. where y is the displacement
from the vertical position equilibrium point, L.

L
y
+

At the equilibrium position, F = mg - kL=0; Then L = mg/k

mg

Let y equal the displacement from the vertical equilibrium point.

At y, the spring exerts an upward force, -k(y + L)
F = mg - k(y + L) = kL - ky - kL = -ky

Note: In this problem, we are turning the spring block

problem sideways; hence we make downward positive.

This is the same expression we used for the horizontal spring block system and it holds
for y positive or negative. Above the equilibrium point (where y <0), the net force
experienced by the block is downward and below the equilibrium point it is upward.
When the block is below its equilibrium point, the spring force is greater than the weight
of the block so it pulls the block up and when the block is above its equilibrium force the
spring force is less than the weight of the block so the block moves down.

Section 14-6: The pendulum

The string is very light; all the mass is concentrated

in the bob.

Length L

mgsin

m
mgcos

We separate the motion into the tangential and radial

directions. Only the tangential component will be used
here.
The equilibrium position is =0 where the pendulum
points straight down.

mg
If we sum forces along s, the tangent to the curve followed by the bob
Ft = -mgsin = md2s
dt2

Then d2 = -gsin
dt2
L

using s = L

s
L

Note that must be expressed in radians. This

can be used as a definition of angles in radians

Provided we stick to trajectories for which is less than about 10o, sin is close to .
Show excel plots on sin, and the % difference vs .
We can write d2 = -g
dt2 L
Solution = maxcos(t + )

which is the equation of motion for SHM. (d2x/dt2 = -k/mx)

Remember x = Acos(t + ) for the block spring

d = -maxsin(t + ) d2 = -2maxcos (t + )
dt
dt2
Then for the pendulum, = g/L and T = 2L/g
Note that the period of oscillation for the pendulum depends only on the length of
the string and the acceleration of gravity.

Problem from a midterm You are asked to build a simple pendulum that will act as a
perfect 'seconds' clock; i.e. one for which each half period is 1.00 second. What will be
the length of this pendulum?
T = 2L/g

then L = gT2/(42) = (9.81m/s2)((2.00s)2)/(42) = 0.994m

Pendulum Problem

L=2.50m

A simple pendulum consists of a mass 7.00kg attached

to light cord of length 2.50m. The mass was observed to
have a velocity of 2.00m/s at it lowest point.

v = 2.00 m/s, m=7.00 kg

a) Find the period: T = 2L/g = 2(2.50m)/(9.81m/s2) = 3.17s
b) Find the total energy: E = K + U = 1/2mvmax2 = 1/2(7.00kg)(2.00m/s)2 = 14.0
joules
c) Find the maximum angular displacement:
Two ways:
(1) at all times = maxcos(t + ) and d/dt = -maxsin(t + )
Now the maximum speed is at the bottom, then (Ld/dt)bottom = vmax = Lmax
Now, = g/L then max = vmax/(L) =vmaxL/g /L = vmax 1/(gL)
= (2.00 m/s)1/[(9.81m/s2)(2.50m)] = 0.404 rad.
Then the maximum angle is 0.404 rad or (0.404 rad)*(180/ deg/rad) = 23.1o

(2) Use conservation of energy to get

max
L
h = L - Lcosmax ; cos max = (L - h)/L
Total energy = 1/2mvmax2 = mgh

h = vmax2/2g = (2.00m/s)2/2(9.81m/s2) = 0.204m

and cosmax = (2.50m - 0.204m)/2.50m = 0.918; max = 0.407 rad
Section 14-7

Damped Harmonic Motion

Ideal fluids <> real fluids viscosity- internal friction

Ideal Oscillators (SHM) <> real oscillators - frictional slowing of the motion of an
oscillator is called damping (damped SHM)

Fv
v

For example, a sphere moving through a fluid experiences a viscous force Fv = -6v
where = fluid viscosity, v = speed of particle. Stokes Law. The - sign is there
because the force is in the opposite direction to the velocity.
We use the general expression that frictional retarding forces follow R = -bv.
b is called the damping constant.
Consider the block-spring problem again:

v
Fk
bv
x
0
Fx = ma = -kx -bv
md2x = -kx - bdx
dt2
dt

The text uses = m/b.

Solution: x = Ae-b/2m tcos(t + ) where = k/m - (b/2m)2

We do not solve this type of

differential equation in this
course.

Note: 1. The amplitude of the oscillations Ae-b/2mt decays exponentially with time.
This is called a damped Oscillator.

Note: 2. The frequency of the oscillations depends upon not only k/m but also b/2m.
= o2 - (b/2m)2 where o = k/m the natural frequency of the oscillator
Note that the damping always slows down the oscillations.
bvmax is the maximum viscous force (occurs at equilibrium point), kA is the maximum
restoring force of the spring (occurs at maximum displacement).
We distinguish three regimes of damping:
Condition
Underdamped
Critically damped
Overdamped

Description
Oscillates, falls to zero
No oscillation, falls to zero
Slow fall to zero

bvmax vs kA
bvmax < kA
bvmax = kA
bvmax > kA

o vs b/2m
o > b/2m
o = b/2m
o < b/2m

A classic example is the shocks in a car. They should be critically damped. With age they
become underdamped and bounce a long time after we pass over a bump. If they are
overdamped, then they don't absorb the shock well.
Whenever friction is present, the energy of the oscillator falls to zero. The lost
mechanical energy goes to the internal energy of the retarding medium. It gets
warm.
Energy in the Damped Oscillator
E = kA2 and A = Aoe-b/2m t
Then E = k Ao2 e-t/ where = m/b is the decay constant for the energy of the
oscillator. Note that energy decays twice as fast as amplitude.
Problem: A Spring block system has spring constant, k = 200 N/m and mass M=200g (a)
Determine the frequency of the oscillation, assuming no damping. (b) It is observed that
after 55 oscillations, the amplitude of the oscillation has dropped to one/half its original
value. Estimate the value of = b/2m. (c) How long does it take the amplitude to
decrease to one-quarter of its original value.

10

(a) Then, = k/M = (200N/m)/.2kg = 31.6 rad/s and f = /2 = 5.03 Hz.

(b) The period of the motion is approximately 1/f = 0.1987s so 55 periods corresponds to
an elapsed time of 55x0.1987s = 10.9s. Then e-t = 0.5 for t=10.9s then -t = ln(0.5) = .693 and = -.693/10.9s = 0.0634 s-1
(c) Solve e-t = 0.25 to get t = -ln(0.25)/ = 21.9s for the amplitude to fall by 1/4 which
corresponds to twice the time to fall by 1/2.
Section 14-8: Driven Oscillations and Resonance
Consider the block- spring system again:
Fext = Focos(t)

This is analogous to pushing a swing.

Fk
-bv
0

Now we have: md2x = Focos(t) - kx - b dx

dt2
dt
Solution of this equation is above our experience in math
If we wait for the system to reach steady state, or equilibrium, we find:
x = Acos(t + ) which looks like the simple oscillator solution but:
A=

Fo/m
( - o ) + (b/m)2
2

2 2

Note: (1) is the frequency of the applied periodic force, o =k/m, the natural
frequency of the oscillator.
Note: (2) There is no damping of the motion since the system is driven by the applied
periodic force.
Note: (3) The amplitude of the oscillations depends on frequency, the closer is to o
the higher the amplitude. When = o, the amplitude peaks. This is called resonance. At
resonance, the applied force is in phase with the velocity and the power transferred to the
oscillator is at a maximum.
Note: (4) The width of the resonance depends on the damping factor b, as b goes to zero,
the width becomes very narrow.
Examples, radio tuner, NMR, breaking wine glass

11

Problem: A 0.150 Kg mass is hanging from a light 6.30N/m spring. The system is driven
by a force oscillating with an amplitude of 1.70N. At what frequency will the force make
the mass vibrate with an amplitude of 0.440 m. Damping is negligible.
The amplitude of the motion is given by
A=
Fo/m
Set b=0 since damping is
2
2 2
negligible
( - o ) + (b/m)2
We have only to solve this problem for . Then
2 -o2 = Fo/(mA) and
= Fo/mA + o2 = 1.70N/(0.150kg*0.440m) + (6.30N/m)/(0.150Kg)
= 8.2 rad/s ; f = 1.31 Hz
End of Oscillations

Using o2 = k/m