Académique Documents
Professionnel Documents
Culture Documents
Assignment # 1: Signals & Systems
Transféré par
Jean HesvetTitre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Assignment # 1: Signals & Systems
Transféré par
Jean HesvetDroits d'auteur :
Formats disponibles
Assignment # 1
ITU (BSEE14)
Signals & Systems
(Publication Date: October 1, 2016)
Due Date: October 14, 2016 0830 hours (start of Friday S&S Lab)
Q1) Sketch the following signals. Clearly label both the axis:
0,
< 4
a) () = { + 2 , 4 < 3
2,
3
b) () = ( 1) () ().
0,
2
c) [] = {2 4, 2 < < 4
4 ,
4
d) [] = [ + 1] [] ()
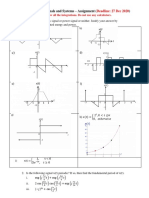
Q2) For each of the following Continuous time signals:
FIG 2A.
FIG 2B.
Apply the following transformations and sketch the results:
i)
() = (2 + 1)
1
3+4
)
2
ii)
() = 2 (
iii)
() = 2[() ()]( 1)
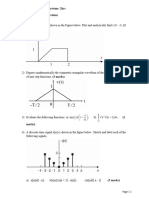
Q3) Sample the given signal in Figure 3 using the following impulse
functions and sketch the results.
FIG 3.
(Hint: sampling is done by using the relation: ()())
1) Impulse/Sampling Function
F ==+
= ( ) ;
2) Impulse/sampling Function
F ==+
= ( );
Where, k = -5,-3, 0, 3, +5
Q4) From the given plots, determine the equation of the sketched signals in
terms of u(t) :
1.
2.
3.
Q5) Decompose the given signals into their even and odd parts. You should
also sketch the signal and its even and odd parts:
2(+3) ( + 3),
2(3) ( 3),
i)
() = {
ii)
iii)
2() ()
iv)
<0
0
Q6) Consider the signal f(t) below:
Express the following signals using only f(t) above and its time-shifted, time-scaled, and
time-inverted versions.
Q7) A discrete time signal x[n] is shown below.
Sketch the following:
Q8).
a) Sketch a voltage signal () = || [( + 4) ( 3)] Volts.
b) Sketch a voltage signal () = 12() where () is the function from the previous problem.
c) Sketch a voltage signal () = (2) where () is function from part (a)
d) Sketch a voltage signal () = ( 2) where () is function from part (a)
e) Applying the voltage signal () across a 1000 resistor (as shown in the figure); sketch the function
() that describes the instantaneous power dissipation of the resistor (R)
Vous aimerez peut-être aussi
- TimeSeriesAnalysis&ItsApplications2e Shumway PDFDocument82 pagesTimeSeriesAnalysis&ItsApplications2e Shumway PDFClaudio Ramón Rodriguez Mondragón91% (11)
- Sanskrit Subhashit CollectionDocument110 pagesSanskrit Subhashit Collectionavinash312590% (72)
- Signals and Systems - Assignment 01 - Signal RepresentationsDocument7 pagesSignals and Systems - Assignment 01 - Signal RepresentationsVIVEK100% (1)
- Assignment 1: Spring 2020Document6 pagesAssignment 1: Spring 2020kant734Pas encore d'évaluation
- 4 WarmupDocument9 pages4 WarmupkrishaPas encore d'évaluation
- Etextbook PDF For Pharmacology Connections To Nursing Practice 3rd EditionDocument61 pagesEtextbook PDF For Pharmacology Connections To Nursing Practice 3rd Editionkarla.woodruff22798% (45)
- Healthymagination at Ge Healthcare SystemsDocument5 pagesHealthymagination at Ge Healthcare SystemsPrashant Pratap Singh100% (1)
- Exponential Smoothing - The State of The ArtDocument28 pagesExponential Smoothing - The State of The ArtproluvieslacusPas encore d'évaluation
- Tutorial 2 Questions 2023Document3 pagesTutorial 2 Questions 2023j2yshjzzsxPas encore d'évaluation
- Signals and SystemsDocument15 pagesSignals and SystemsAryan VermaPas encore d'évaluation
- SE 2008 ElectricalDocument46 pagesSE 2008 ElectricalMuhammad MujtabaPas encore d'évaluation
- Tutorial 1Document8 pagesTutorial 1Carine ChiaPas encore d'évaluation
- Tutorial - Chapter 3 (3.1 - 3.4)Document1 pageTutorial - Chapter 3 (3.1 - 3.4)zul hilmiPas encore d'évaluation
- Assignment5 CLO3-SolDocument11 pagesAssignment5 CLO3-SolMuhammad AbdullahPas encore d'évaluation
- Tutorial 2 SignalsDocument3 pagesTutorial 2 SignalsSahilYadavPas encore d'évaluation
- 20ecpc303 Ss QB Ese StuDocument18 pages20ecpc303 Ss QB Ese Studheenadhaya902Pas encore d'évaluation
- 20ecpc303 Ss QB Ese StuDocument19 pages20ecpc303 Ss QB Ese Stuakalan803Pas encore d'évaluation
- Basic Operations On Signals 2Document3 pagesBasic Operations On Signals 2physicist sharmaPas encore d'évaluation
- QuizDocument6 pagesQuiznaimPas encore d'évaluation
- EEB731 Signals and Systems: Tutorial 2 Q1Document2 pagesEEB731 Signals and Systems: Tutorial 2 Q1Prince RaynalPas encore d'évaluation
- Ee8591 DSP Model 1Document3 pagesEe8591 DSP Model 1Ece DeptPas encore d'évaluation
- Me 314 Signals and Systems Questions BankDocument5 pagesMe 314 Signals and Systems Questions BankAri BaderPas encore d'évaluation
- Signals and Systems EEEB233 Tutorial 1 (Due Date: 19.06.2015 5.30pm)Document2 pagesSignals and Systems EEEB233 Tutorial 1 (Due Date: 19.06.2015 5.30pm)zawirPas encore d'évaluation
- 203 EEE 2301 Assignment 1Document2 pages203 EEE 2301 Assignment 1Faizur Rahman PaponPas encore d'évaluation
- Assignment-1Document3 pagesAssignment-1Prashanna YadavPas encore d'évaluation
- DSP Online Mid Exam 2020Document2 pagesDSP Online Mid Exam 2020Vishal KevatPas encore d'évaluation
- STAT721 Test1 2022 SolutionsDocument5 pagesSTAT721 Test1 2022 SolutionsJacquiline IsaacPas encore d'évaluation
- Question 1 (20 Marks) : Mathematics For Technology II Sample Test - Marking Scheme Page 1 of 5Document5 pagesQuestion 1 (20 Marks) : Mathematics For Technology II Sample Test - Marking Scheme Page 1 of 5Mohammed ABDO ALBAOMPas encore d'évaluation
- Tutorial1 PDFDocument2 pagesTutorial1 PDFVisakan ParameswaranPas encore d'évaluation
- ECE633 Signals and Systems I, Fall 2009 - Homework 2 SolutionsDocument13 pagesECE633 Signals and Systems I, Fall 2009 - Homework 2 SolutionsGabrielPopoola13100% (2)
- ICM2008 Communication Systems: 2015 - Tutorial 1 Work SheetDocument1 pageICM2008 Communication Systems: 2015 - Tutorial 1 Work SheetMathew ClewlowPas encore d'évaluation
- F3478signal Systems TutorialDocument10 pagesF3478signal Systems TutorialAnkit KhannaPas encore d'évaluation
- Tutorial Sheet-1Document1 pageTutorial Sheet-1Sayeed HabeebPas encore d'évaluation
- Matemáticas II: Tarea Semanal # 1 Unidad # 1Document7 pagesMatemáticas II: Tarea Semanal # 1 Unidad # 1Nani brockPas encore d'évaluation
- United International University (Uiu)Document2 pagesUnited International University (Uiu)Faizur Rahman PaponPas encore d'évaluation
- BMS College of Engineering, Bangalore-560019: July / August 2017 Supplementary Semester ExaminationsDocument3 pagesBMS College of Engineering, Bangalore-560019: July / August 2017 Supplementary Semester Examinationskoushik bhatPas encore d'évaluation
- EEE243/ECE243 Signals and Systems - Assignment : Please Show All The Integrations. Do Not Use Any CalculatorsDocument5 pagesEEE243/ECE243 Signals and Systems - Assignment : Please Show All The Integrations. Do Not Use Any CalculatorsRedwan AhmedPas encore d'évaluation
- SLS Assignment 1Document3 pagesSLS Assignment 1Abdullah MohasienPas encore d'évaluation
- Assignment 2Document3 pagesAssignment 2Laith Al-KinaniPas encore d'évaluation
- DSP QB Updated - NewDocument7 pagesDSP QB Updated - NewthenithyanagrajPas encore d'évaluation
- 2 Signals and Systems: Part I: Solutions To Recommended ProblemsDocument9 pages2 Signals and Systems: Part I: Solutions To Recommended ProblemssamibdzPas encore d'évaluation
- Tutorial AssignmentDocument2 pagesTutorial AssignmentPartha Pratim RoyPas encore d'évaluation
- MCTE4185 - SP22 - HW2 (+answers)Document2 pagesMCTE4185 - SP22 - HW2 (+answers)Nasser ÀlsalmiPas encore d'évaluation
- RepositoryDocument17 pagesRepositoryarefinhasib07Pas encore d'évaluation
- Mid 1Document3 pagesMid 1baris0oPas encore d'évaluation
- 15ECE204 - I Ass Aug 2019Document2 pages15ECE204 - I Ass Aug 2019mahamaniPas encore d'évaluation
- SS Dec 18Document4 pagesSS Dec 18SAURABH BHISEPas encore d'évaluation
- Quantum Mechanics II - Homework 10Document7 pagesQuantum Mechanics II - Homework 10Ale GomezPas encore d'évaluation
- Vector Product and Systems in Balance: Juan Sebastian Ballen Villalba September 2019Document6 pagesVector Product and Systems in Balance: Juan Sebastian Ballen Villalba September 2019Sebastián BallenPas encore d'évaluation
- UMA001Document1 pageUMA001Rishabh SinghalPas encore d'évaluation
- Tutorial 3 SolutionDocument5 pagesTutorial 3 SolutionMuhanad OfficerPas encore d'évaluation
- MCR 3u Exam ReviewDocument5 pagesMCR 3u Exam ReviewStarLink1Pas encore d'évaluation
- CA Exam On Signal and SystemsDocument2 pagesCA Exam On Signal and SystemsMBIEDA NGOMEGNI FRANK GAETANPas encore d'évaluation
- مرشحات برمجة .Document12 pagesمرشحات برمجة .سجاد هاشم ألعيبي محيسن -BPas encore d'évaluation
- Name: - 2K14-EE - Submission DateDocument2 pagesName: - 2K14-EE - Submission DateUsmanAliPas encore d'évaluation
- Sns2012 - Practice Problem 1Document3 pagesSns2012 - Practice Problem 1ashar565Pas encore d'évaluation
- Assignment All+Sem+II+20132014Document115 pagesAssignment All+Sem+II+20132014Azlin HazwaniPas encore d'évaluation
- Johns Hopkins University: - AM - BMDocument2 pagesJohns Hopkins University: - AM - BMroyhibbertliterallyPas encore d'évaluation
- Matlab AnswersDocument16 pagesMatlab AnswersChristelle Kaye BisnarPas encore d'évaluation
- Fall 2007 Math 151 Common Exam 3B Tue, 27/nov/2007: InstructionsDocument10 pagesFall 2007 Math 151 Common Exam 3B Tue, 27/nov/2007: Instructionskaus9199Pas encore d'évaluation
- 2 Array and Matrix Operations PDFDocument39 pages2 Array and Matrix Operations PDFAugusto De La Cruz CamayoPas encore d'évaluation
- Continuous Time Signals Part I Fourier SeriesDocument12 pagesContinuous Time Signals Part I Fourier SeriesbusybeePas encore d'évaluation
- Analytic Geometry: Graphic Solutions Using Matlab LanguageD'EverandAnalytic Geometry: Graphic Solutions Using Matlab LanguagePas encore d'évaluation
- Toshiba MotorsDocument16 pagesToshiba MotorsSergio Cabrera100% (1)
- Operations Management Interim ProjectDocument4 pagesOperations Management Interim ProjectABAYANKAR SRIRAM (RA1931201020042)Pas encore d'évaluation
- DS Important QuestionsDocument15 pagesDS Important QuestionsLavanya JPas encore d'évaluation
- SavannahHarbor5R Restoration Plan 11 10 2015Document119 pagesSavannahHarbor5R Restoration Plan 11 10 2015siamak dadashzadePas encore d'évaluation
- A 138Document1 pageA 138pooja g pPas encore d'évaluation
- Lancru hzj105 DieselDocument2 pagesLancru hzj105 DieselMuhammad MasdukiPas encore d'évaluation
- SOCIAL MEDIA DEBATE ScriptDocument3 pagesSOCIAL MEDIA DEBATE Scriptchristine baraPas encore d'évaluation
- PGCRSM-01-BLOCK-03 Research Design ExperimentalDocument29 pagesPGCRSM-01-BLOCK-03 Research Design ExperimentalVijilan Parayil VijayanPas encore d'évaluation
- CTS2 HMU Indonesia - Training - 09103016Document45 pagesCTS2 HMU Indonesia - Training - 09103016Resort1.7 Mri100% (1)
- Week - 2 Lab - 1 - Part I Lab Aim: Basic Programming Concepts, Python InstallationDocument13 pagesWeek - 2 Lab - 1 - Part I Lab Aim: Basic Programming Concepts, Python InstallationSahil Shah100% (1)
- Muscles of The Dog 2: 2012 Martin Cake, Murdoch UniversityDocument11 pagesMuscles of The Dog 2: 2012 Martin Cake, Murdoch UniversityPierePas encore d'évaluation
- RN42Document26 pagesRN42tenminute1000Pas encore d'évaluation
- Sap New GL: Document Splitting - Configuration: ChooseDocument3 pagesSap New GL: Document Splitting - Configuration: ChooseChandra Sekhar PPas encore d'évaluation
- Second Conditional Conversation QuestionsDocument2 pagesSecond Conditional Conversation QuestionsEdith Salomé PinosPas encore d'évaluation
- John Wren-Lewis - NDEDocument7 pagesJohn Wren-Lewis - NDEpointandspacePas encore d'évaluation
- Algorithms For Automatic Modulation Recognition of Communication Signals-Asoke K, Nandi, E.E AzzouzDocument6 pagesAlgorithms For Automatic Modulation Recognition of Communication Signals-Asoke K, Nandi, E.E AzzouzGONGPas encore d'évaluation
- 2023 Teacher Email ListDocument5 pages2023 Teacher Email ListmunazamfbsPas encore d'évaluation
- International Freight 01Document5 pagesInternational Freight 01mature.ones1043Pas encore d'évaluation
- RECYFIX STANDARD 100 Tipe 010 MW - C250Document2 pagesRECYFIX STANDARD 100 Tipe 010 MW - C250Dadang KurniaPas encore d'évaluation
- Dynalift Sed0804679lDocument1 pageDynalift Sed0804679lzaryab khanPas encore d'évaluation
- Introduction To Password Cracking Part 1Document8 pagesIntroduction To Password Cracking Part 1Tibyan MuhammedPas encore d'évaluation
- Music 9 Q3 Mod4 Musical Elements of Given Romantic Period PiecesDocument19 pagesMusic 9 Q3 Mod4 Musical Elements of Given Romantic Period PiecesFinn Daniel Omayao100% (1)
- G1000 Us 1014 PDFDocument820 pagesG1000 Us 1014 PDFLuís Miguel RomãoPas encore d'évaluation
- FINAL BÁO-CÁO-THỰC-TẬP.editedDocument38 pagesFINAL BÁO-CÁO-THỰC-TẬP.editedngocthaongothi4Pas encore d'évaluation
- Barrett Beyond Psychometrics 2003 AugmentedDocument34 pagesBarrett Beyond Psychometrics 2003 AugmentedRoy Umaña CarrilloPas encore d'évaluation
- Vygotsky EssayDocument3 pagesVygotsky Essayapi-526165635Pas encore d'évaluation