Académique Documents
Professionnel Documents
Culture Documents
The Lihnard-Wiechert Potentials Moving Point Charge: J (R, Ro (T) )
Transféré par
EddieTitre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
The Lihnard-Wiechert Potentials Moving Point Charge: J (R, Ro (T) )
Transféré par
EddieDroits d'auteur :
Formats disponibles
10.
3 The Liknard-Wiechert Potentials of a Moving Point Charge 215
Now we use the relation
W
K
c l dksinAkcsinBkc= - - [ 6 ( A + B ) -6(A - B ) ] ,
2
which can be verified by replacing the sines by exponentials and using the integral representation
of the one-dimensional delta function. Thus G can be expressed as the sum of two delta function
contributions, i.e. we obtain
Since the argument of the second delta function is nowhere zero for t > t’ this cannot contribute
t o G. We thus obtain
(10.25)
This Green’s function describes the effect at time t > t’ and at radius T > T’ of a delta function-like
cause at time t = t‘ and radius T = T’ propagating from the source with the velocity of light.
10.3 The Lihnard-Wiechert Potentials of a Moving
Point Charge
Our aim is now to calculate the potentials $(r,t),A(r,t) for the case of
a point charge moving with velocity v ( t ) . The very important results we
obtain are the so-called Liknard- Wiechert potentials. We expect, of course,
to regain in the limit of vanishing velocity the well known static expressions
we had before.
We let ro(t) be the vector representing the path or trajectory of the point
charge e and set
v(t)= ro(t)
for its velocity. The charge density can then be written
and the current density
j(r, t ) = p(r, t)v(t)= ev(t)6(r - ro(t)). (10.27)
We consider first the scalar potential 4. Inserting into Eq. (10.17) the
Vous aimerez peut-être aussi
- Radiation Moving Charges: Potentials and Fields of A Moving Point ChargeDocument25 pagesRadiation Moving Charges: Potentials and Fields of A Moving Point Chargeosama hasanPas encore d'évaluation
- Unit 12 Line and Surf'Ace IntegralsDocument60 pagesUnit 12 Line and Surf'Ace IntegralsRiddhima MukherjeePas encore d'évaluation
- Phaseur FourierDocument11 pagesPhaseur FourierAndrew JonesPas encore d'évaluation
- Liénard-Wiechert Potentials Describe The ClassicalDocument11 pagesLiénard-Wiechert Potentials Describe The ClassicalJithin PrasadPas encore d'évaluation
- Quantum Mechanics Midterm: Scattering, Harmonic Oscillator, Morse PotentialDocument4 pagesQuantum Mechanics Midterm: Scattering, Harmonic Oscillator, Morse PotentialDipankar AdhikaryPas encore d'évaluation
- CH01Document46 pagesCH01Alejandro CarbajalPas encore d'évaluation
- Quantenoptik Vorlesung6 PDFDocument11 pagesQuantenoptik Vorlesung6 PDFErinSuttonPas encore d'évaluation
- Et M Zulassungspruefung PDFDocument5 pagesEt M Zulassungspruefung PDFmuhammad bilalPas encore d'évaluation
- Periodic Systems and The Bloch TheoremDocument11 pagesPeriodic Systems and The Bloch TheoremCamiloUlloaPas encore d'évaluation
- Doctors 2023Document24 pagesDoctors 2023Helen DoctorsPas encore d'évaluation
- ELE 301, Fall 2010 Laboratory No. 7 Stability and Root Locus PlotsDocument4 pagesELE 301, Fall 2010 Laboratory No. 7 Stability and Root Locus PlotsAnonymous WkbmWCa8MPas encore d'évaluation
- Relatividad GeneralDocument64 pagesRelatividad GenerallacrimogenoPas encore d'évaluation
- Rasheef Maths AssignmantDocument10 pagesRasheef Maths AssignmantMohamed SanoosPas encore d'évaluation
- Quantum Physics I (8.04) Spring 2016 Assignment 9: Problem Set 9Document5 pagesQuantum Physics I (8.04) Spring 2016 Assignment 9: Problem Set 9Fabian M Vargas FontalvoPas encore d'évaluation
- Lec10 SHMDocument7 pagesLec10 SHMDr Srini vasanPas encore d'évaluation
- Ideal Fermi Gas: 13.1 Equation of StateDocument14 pagesIdeal Fermi Gas: 13.1 Equation of StateShalltear BloodFallenPas encore d'évaluation
- Exercises 2Document7 pagesExercises 2andre130912Pas encore d'évaluation
- Rho Is Invariant Under BoostDocument2 pagesRho Is Invariant Under Boost张泽华Pas encore d'évaluation
- Doppler Broadening: 1 Wavelength and TemperatureDocument5 pagesDoppler Broadening: 1 Wavelength and Temperatureakhilesh_353859963Pas encore d'évaluation
- Matlab Simulink DC MotorDocument12 pagesMatlab Simulink DC Motorkillua142100% (4)
- Vector IntegrationDocument32 pagesVector Integrationanon_479876439Pas encore d'évaluation
- Solutions 1.8-Page 89 Problem 2: e V T V e X T XDocument8 pagesSolutions 1.8-Page 89 Problem 2: e V T V e X T Xukel de guzmanPas encore d'évaluation
- Rollercoaster Math Design Using FunctionsDocument18 pagesRollercoaster Math Design Using FunctionsNathan Smith100% (2)
- The Transfer Function PDFDocument15 pagesThe Transfer Function PDFArnav KushwahaPas encore d'évaluation
- Radiation from Accelerating Charges ExplainedDocument19 pagesRadiation from Accelerating Charges Explainedhammoudeh13Pas encore d'évaluation
- Design of Velometer PDFDocument12 pagesDesign of Velometer PDFHimanshu100% (1)
- Determining Kinetic MotionDocument9 pagesDetermining Kinetic MotionĐình TháiPas encore d'évaluation
- Electrostatics in Vacuum - 1673699222Document73 pagesElectrostatics in Vacuum - 1673699222Jigyarth SharmaPas encore d'évaluation
- Mechanics 1: Projectiles, Constrained Motion & FrictionDocument7 pagesMechanics 1: Projectiles, Constrained Motion & Frictionsoumengoswami10Pas encore d'évaluation
- Qualifier Study Guide: Office 221 Department of Physics, Florida State University, Tallahassee, FL 32308Document17 pagesQualifier Study Guide: Office 221 Department of Physics, Florida State University, Tallahassee, FL 32308Hussein AlghoulPas encore d'évaluation
- A F Nan ScatteringDocument32 pagesA F Nan ScatteringkrishnaPas encore d'évaluation
- RC-RL and RLC CircuitsDocument15 pagesRC-RL and RLC CircuitsHaris Noushahi50% (2)
- Chapter 3Document15 pagesChapter 3Gemechis AsfawPas encore d'évaluation
- General Relativity 4Document13 pagesGeneral Relativity 4HarshitPas encore d'évaluation
- Chapter 2: Network Transform Representation and Analysis: (Type The Document Title)Document9 pagesChapter 2: Network Transform Representation and Analysis: (Type The Document Title)kidanemariam tesera100% (1)
- ExamDocument3 pagesExamLionel CarlosPas encore d'évaluation
- Basic Theory For Wind Turbine Blade Aerodynamics: P M Mohan Das & R S AmanoDocument13 pagesBasic Theory For Wind Turbine Blade Aerodynamics: P M Mohan Das & R S AmanoAnkur MaheshwariPas encore d'évaluation
- PSA Lab 1 ReportDocument7 pagesPSA Lab 1 ReportMovie Trailers blazePas encore d'évaluation
- Akhil Math IA Properties of AC CircuitsDocument12 pagesAkhil Math IA Properties of AC CircuitsJordy Van KollenburgPas encore d'évaluation
- Nearly-Free Electrons Model: Jacob Shapiro December 18, 2012Document7 pagesNearly-Free Electrons Model: Jacob Shapiro December 18, 2012nouserhere123Pas encore d'évaluation
- Tamm States and Surface Electronic StructureDocument17 pagesTamm States and Surface Electronic StructureRyan BaliliPas encore d'évaluation
- M15 Mazu0536 01 Ism C15Document22 pagesM15 Mazu0536 01 Ism C15Luphumlo GolelaPas encore d'évaluation
- 13 - Ideal - Fermi - Gas - BookletDocument8 pages13 - Ideal - Fermi - Gas - Bookletkoulickchakraborty5555Pas encore d'évaluation
- Updating The QR Factorization and The Least Squares Problem (2008)Document73 pagesUpdating The QR Factorization and The Least Squares Problem (2008)Eran MaromPas encore d'évaluation
- RC Circuits and Applications: Lab Ticket and Write-Up CommentsDocument12 pagesRC Circuits and Applications: Lab Ticket and Write-Up CommentsSatyajit MorePas encore d'évaluation
- 08 (T) - Alternating CurrentDocument17 pages08 (T) - Alternating CurrentDurgesh YadavPas encore d'évaluation
- Problem SetDocument12 pagesProblem SetDWARAM VENKATA SUBBA REDDY 1816Pas encore d'évaluation
- The Relationship of The Cotangent Function To Special Relativity Theory, Silver Means, P-Cycles, and Chaos TheoryDocument14 pagesThe Relationship of The Cotangent Function To Special Relativity Theory, Silver Means, P-Cycles, and Chaos Theorypipul36Pas encore d'évaluation
- Trans LinesDocument8 pagesTrans LinesariehashimiePas encore d'évaluation
- Leaky Integrator RC CircuitDocument14 pagesLeaky Integrator RC CircuitMUSAIB UL FAYAZ 2022 17Pas encore d'évaluation
- s00006 016 0722 6 PDFDocument25 pagess00006 016 0722 6 PDFZow NiakPas encore d'évaluation
- Griffiths - Introduction To Quantum Mechanics-29-32Document12 pagesGriffiths - Introduction To Quantum Mechanics-29-32Annisa MadiunPas encore d'évaluation
- Calculus 3Document2 pagesCalculus 3simbachipsyPas encore d'évaluation
- Problems in Quantum Mechanics: Third EditionD'EverandProblems in Quantum Mechanics: Third EditionÉvaluation : 3 sur 5 étoiles3/5 (2)
- Interactions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsD'EverandInteractions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsPas encore d'évaluation
- The Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64D'EverandThe Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64Pas encore d'évaluation
- C*-Algebra Extensions and K-Homology. (AM-95), Volume 95D'EverandC*-Algebra Extensions and K-Homology. (AM-95), Volume 95Pas encore d'évaluation
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)D'EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)Pas encore d'évaluation
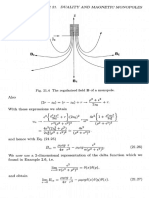
- Duality A ND Magnetic Monopoles: Fig. 21.4 The Regularised Field of MonopoleDocument1 pageDuality A ND Magnetic Monopoles: Fig. 21.4 The Regularised Field of MonopoleEddiePas encore d'évaluation
- Duality A N D Magnetic MonopolesDocument1 pageDuality A N D Magnetic MonopolesEddiePas encore d'évaluation
- Panorama B1 Deutsch Als Fremdsprache (Ulrike Würz)Document187 pagesPanorama B1 Deutsch Als Fremdsprache (Ulrike Würz)Neža Zupančič100% (2)
- Ch2 Coulomb's LawDocument44 pagesCh2 Coulomb's Lawmehdii.heidary136686% (7)
- Chapter 21. Duality A N D Magnetic Monopoles: Regularisation The Monopole FieldDocument1 pageChapter 21. Duality A N D Magnetic Monopoles: Regularisation The Monopole FieldEddiePas encore d'évaluation
- The Delta: DistributionDocument1 pageThe Delta: DistributionEddiePas encore d'évaluation
- POCSS ( ) S (Y S ( ) .: ConcludingDocument1 pagePOCSS ( ) S (Y S ( ) .: ConcludingEddiePas encore d'évaluation
- Seem To Be Singular At: r3 (J ."TS"Document1 pageSeem To Be Singular At: r3 (J ."TS"EddiePas encore d'évaluation
- 250 PDFDocument1 page250 PDFEddiePas encore d'évaluation
- M, Po (H + M) - H: Macroscopic MagnetostaticsDocument1 pageM, Po (H + M) - H: Macroscopic MagnetostaticsEddiePas encore d'évaluation
- 411Document1 page411EddiePas encore d'évaluation
- Introduction EqDocument1 pageIntroduction EqEddiePas encore d'évaluation
- Solutions HW5Document4 pagesSolutions HW5Far Away Archipelago50% (4)
- AN THE Between Magnetic: Analytic Solution For Force TWO DipolesDocument14 pagesAN THE Between Magnetic: Analytic Solution For Force TWO DipolesEddiePas encore d'évaluation
- 14.9 Energy Transport in Wave Guides: D Z D L, Where DL Is An Element of The PathDocument1 page14.9 Energy Transport in Wave Guides: D Z D L, Where DL Is An Element of The PathEddiePas encore d'évaluation
- HW 3 CMDocument9 pagesHW 3 CMeddiejam1642Pas encore d'évaluation
- 33 PDFDocument1 page33 PDFEddiePas encore d'évaluation
- On The Choice of Units: But atDocument1 pageOn The Choice of Units: But atEddiePas encore d'évaluation
- Teoria de Grupos para Fisicos Rodolfo Alexander DiazDocument391 pagesTeoria de Grupos para Fisicos Rodolfo Alexander DiazGerman ChiappePas encore d'évaluation
- 14.5 Fundamental Equations The Coaxial Cable: GuidesDocument1 page14.5 Fundamental Equations The Coaxial Cable: GuidesEddiePas encore d'évaluation
- Solutions Manual To Irodov General Problems in Physics - Mechanics - Problems From 76 To 100Document30 pagesSolutions Manual To Irodov General Problems in Physics - Mechanics - Problems From 76 To 100EddiePas encore d'évaluation
- The Comprehensive L TEX Symbol ListDocument338 pagesThe Comprehensive L TEX Symbol Listgabomath2010Pas encore d'évaluation
- Electromagnetic Waves in VacuumDocument1 pageElectromagnetic Waves in VacuumEddiePas encore d'évaluation
- Chap 3Document17 pagesChap 3Yessenia Madrid100% (1)
- Teoria de Grupos para Fisicos Rodolfo Alexander DiazDocument391 pagesTeoria de Grupos para Fisicos Rodolfo Alexander DiazGerman ChiappePas encore d'évaluation
- (E - D + H - B) V - (E X H) + J - e .: R, L I RDocument1 page(E - D + H - B) V - (E X H) + J - e .: R, L I REddiePas encore d'évaluation
- 88 PDFDocument1 page88 PDFEddiePas encore d'évaluation
- Magne Tostatics: B (R) - K'V (IR)Document1 pageMagne Tostatics: B (R) - K'V (IR)EddiePas encore d'évaluation
- Themaxwell Equations: LoopDocument1 pageThemaxwell Equations: LoopEddiePas encore d'évaluation