Académique Documents
Professionnel Documents
Culture Documents
AP Calculus AB Study Sheet
Transféré par
Kohji Ashitaka SugiokaDescription originale:
Titre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
AP Calculus AB Study Sheet
Transféré par
Kohji Ashitaka SugiokaDroits d'auteur :
Formats disponibles
Mar 13
AP Calculus AB Study Sheet
1 of 4
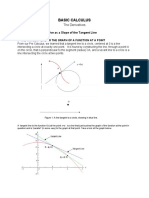
KEY DEFINITIONS
limit this is what distinguishes Calculus from other math. A limit of a function is the value that the dependent variable approaches as the independent variable approaches a given value. A limit has the general form lim x h f x This gives the value that the function is tending toward as x approaches h. derivative this describes the slope of the graph, or the rate of change of the function. The derivative may be dy d [ y] . Each of these examples given refers to "THE notated in many ways, including y ' , , and dx dx DERIVATIVE OF Y WITH RESPECT TO X." To use function notation, the derivative of f x is f ' x . The limit f x h f x definition of derivative is lim h0 h differential a special variable used in taking derivatives and solving differential equations. A differential equation is solved by integration. implicit differentiation useful when there are multiple variables in the expression. When the derivative is taken, simply multiply by the corresponding differential. integral this describes the area under the curve. The integral is the inverse of the derivative, and thus is also called the anti-derivative. Notation is one of two ways: f x dx or F x In the latter case, it cannot be assumed that F always means the anti-derivative of f. The above examples are indefinite integrals, meaning that they give a general solution. When evaluating a definite integral, the result is the area under the curve. Definite b f x from a to b. integrals have the form f x dx ; this example will yield the area under
critical numbers these are the values of the independent variable at which the first derivative is zero: f ' x =0 . They also occur where the first derivative is undefined, such as at a cusp or sharp corner (like absolute value). These numbers are useful when looking for changes in the trend of the graph: either increasing or decreasing. Critical numbers also indicate relative extrema, either relative maxima or relative minima. absolute extrema absolute maxima and minima must be found by using CRITICAL NUMBERS and the ENDPOINTS OF THE INTERVAL. Whichever value is furthest to the desired extreme is given as the absolute extrema. inflection inflection is the change of the concavity of the graph. A graph is either concave up or concave down (a horizontal line would have both or none) Points of inflection occur where the second derivative is zero. Evaluation of the second derivative at any value yields the concavity; f ' ' x 0 concave up ; f ' ' x 0 concave down mean value theorem (for derivatives) this theorem declares that there must be at least one point on a given interval for which the instantaneous slope (derivative) equals the average rate of change over that interval. The function must be continuous on the closed interval, and differentiable on the open interval. Symbolically, this is f b f a expressed f ' c = where a , b is the open interval. ba Rolle's theorem this is a simpler version, and an application of the mean value theorem. It adds the condition that, on the interval a , b , f a= f b . This means that the average slope is zero, and there must be a point c at which f ' c =0 position, velocity, and acceleration that's the order, a t=v ' t = s' ' t or s t= v t dt = [ a t dt ] dt
Mar 13
AP Calculus AB Study Sheet
2 of 4
DERIVATIVES
For all of the following, x is considered to be the independent variable, n is a real number, c is a nonzero real number, a is a positive integer, and u and v are differentiable functions. d d n [ f u]= f ' u u ' [ x ]=nxn1 Simple Power Rule: Chain Rule: dx dx d d u' d u' [cu ]=cu ' [log a u]= [arctan u ]= 1. 11. 21. dx dx ln a u dx 1u 2 d d u d u ' [uv ]=u' v ' [a ]= ln a a u u ' 2. 12. [arccot u ]= 22. dx dx dx 1u 2 d d d u' [uv ]=uv ' vu ' Product Rule 13. [sin u ]=cos u u' 3. 23. dx [arcsec u]= dx dx u u2 1 d d u vu 'uv ' d u ' [cos u ]=sin u u ' = 4. Quotient Rule 14. 2 dx dx v 24. dx [arccsc u]= v u u 21 d 2 d [tan u]=sec u u ' 15. [c ]=0 5. d x 1 dx [arcsin ]= 2 2 dx 25. dx a a x d d n [cot u]=csc 2 u u ' 16. [u ]=nu n1 u ' 6. d x 1 dx dx [arccos ]= 2 2 26. dx a a x d d [sec u]=sec u tan u u ' 17. [ x ]=1 7. dx d x a dx [arctan ]= 2 2 27. d dx a a x d u [csc u]= csc u cot u u ' 18. [u]= u' , u0 8. dx d x a dx u [arccot ]= 2 2 28. d u' d u' dx a a x [arcsin u ]= 19. [ln u]= 9. dx 1u 2 dx u d x a 29. dx [arcsec a ]= d u' d u u x x 2a 2 [arccos u ]= [e ]=e u ' 10. 20. 2 dx dx 1u d x a 30. dx [arccsc a ]= x x 2a 2
[]
Mar 13
AP Calculus AB Study Sheet
3 of 4
INTEGRALS
For all of the following, k, C, and n are real numbers; u is a differentiable function. 1. k f u du=k f u du 11. cot u du=lnsin uC 2. [ f u g u] du= f u du g u du 12. sec u du=lnsec utan uC 3. du=uC General rule 13. csc u du=lncsc ucot uC n1 2 u 14. sec u du=tan uC 4. u n du= C , n1 General rule 2 n1 15. csc u du=cot uC du 5. =lnuC 16. sec u tan u du=sec uC u u u 17. csc u cot u du=csc uC 6. e du=e C du u 1 u u 18. 2 2 =arcsin C a C 7. a du= a a u ln a du 1 u 8. sin u du=cos uC 19. 2 2 = arctan C a a u a 9. cos u du=sin uC u du 1 = arcsec C 20. 10. tan u du=lncos uC 2 2 a a u u a
Fundamental Theorem of Calculus this multi-part theorem is very important! b Part 1: a f x dx= F b F a that is to say, that once the anti-derivative of the function is found
(usually using the simple power rule for integrals), the integral on the closed interval [ a , b] is equal to the difference in the anti-derivatives at each endpoint. x d Part 2: a f t dt = f x or F ' x= f x This states that the derivative of the anti-derivative is dx the original function. Be careful applying this, though. The example given takes the integral over [ a , x ] , but if x is a differentiable function, you must use the chain rule eventually.
The Mean Value Theorem for Integrals if f is continuous on the closed interval [a,b] then there exists a b number c in the closed interval [a,b] such that a f x dx= f c ba This means that there exists a rectangle such that its area is equal to the area of the region under the curve. average value the mean height of a function on the open interval a , b is
b 1 a f u du ba
area between two curves the basic concept here is that the area between two curves is equal to the total area from the upper curve to the zero line, minus the area from the lower curve to the zero line. For all real numbers a and b as the endpoints of the interval, for an upper function f(x) and lower function g(x), the area between them is b b b a [ f x g x] dx=a f x dxa g x dx To use this formula, f(x) must be greater than g(x) over the entire interval. Likewise, everything could be done in terms of y: For all real numbers a and b as the endpoints of the interval, for an upper function f(y) and lower function g(y), the area between them is b b b a [ f y g y] dy=a f y dya g y dy To use this formula, f(x) must be greater than g(x) over the entire interval (This means f(x) is farther to the right!).
Mar 13
AP Calculus AB Study Sheet
4 of 4
VOLUMES OF SOLIDS OF REVOLUTION
Representative Rectangles Remember the Reimann sums that explained the integral concept? This is the same thing. When we say representative rectangles in solids of revolution, we mean a little strip of the region that will be revolved around the axis of revolution to become either a disk, washer, or shell. Axis of Revolution This is a line about which a two-dimensional region is revolved to become a threedimensional solid. The Disk Method This method may be used when representative rectangles are perpendicular to the axis of rotation, and when the region to be revolved is flush with the axis of revolution over the entire interval. The formula is based on the area formula for a circle, A= r 2 . Instead of a simple quantity r, we have an entire function represented as R(x).There are two versions of the formula, one dealing with horizontal axes of revolution b b and one with vertical. V = a [ R x ]2 dx or a [ R y]2 dy The Washer Method The washer method is identical to the Disk Method, except for one condition: the region to be revolved need not be flush with the axis of revolution; in fact, it might not touch it at all! The representative rectangles still need to be perpendicular to the axis of revolution. The formula is b b V =a [ R x]2 [ r x ]2 dx or a [ R y ]2 [r y ]2 dy R(x) must be greater than r(x) over the entire interval, and likewise for y. The Shell Method This one is different. The region need not be flush with the axis of revolution, and the representative rectangles must be parallel to the axis of revolution. The volume formula is an application of the circumference of a circle, C=2 r . In the shell method, p(x) is the distance of the rectangle from the axis of revolution, and h(x) is the height of the rectangle. When writing the integral, make sure that if everything is in terms of x, and there is a dx at the end, that the limits of integration are also x-values! Everything may be applied b b to functions in terms of y. V =2 a p x h x dx or 2 a p y h y dy Volumes of Known Cross-Sections This is a strange concept. Basically, you want to make a region pop out of the page by placing a certain shape on it. For example, take the region shown below. Place a vertical SQUARE on each x-value. The size of the square changes at each location, and is dependent on the vertical height of the region. This dependent value is known as the base. The base is used to calculate the area of the b pop-out for each x from a to b. Always use vertical rectangles. V =a A x dx You'll need some area formulas to do all of this right! (Notice that most have a b2 term) Cross-Section Area Formula Square Equilateral Triangle Isosceles Right Triangle (Hint: the right angle is opposite the base) Semi-circle Rectangle (of given height h)
A x =b 2
3 A x = b 2 4 1 A x = b2 4 1 A x = b2 8 A x =bh
Vous aimerez peut-être aussi
- Multivariable Calculus Review SheetDocument2 pagesMultivariable Calculus Review SheetSteven Walker100% (1)
- Curvature: PrerequisitesDocument14 pagesCurvature: PrerequisitesmathplazaPas encore d'évaluation
- Appendix A 2Document6 pagesAppendix A 2ErRajivAmiePas encore d'évaluation
- AP Calculus AB - Ultimate Guide Notes - KnowtDocument29 pagesAP Calculus AB - Ultimate Guide Notes - Knowtcondyerhaze1Pas encore d'évaluation
- AP Calculus Cheat SheetDocument2 pagesAP Calculus Cheat Sheet3d5w2dPas encore d'évaluation
- Mcmain SolidsofrevolutionDocument15 pagesMcmain Solidsofrevolutionapi-280902734Pas encore d'évaluation
- Curve Sketching Is Another Practical Application of Differential CalculusDocument11 pagesCurve Sketching Is Another Practical Application of Differential CalculusAmmad ImamPas encore d'évaluation
- Differentiation & Maxima & MinimaDocument30 pagesDifferentiation & Maxima & Minimaakki2511Pas encore d'évaluation
- AP Calculus BC Study GuideDocument5 pagesAP Calculus BC Study GuideJohn MoonPas encore d'évaluation
- Algebra Integrals and IntegrationDocument4 pagesAlgebra Integrals and IntegrationBharath KumarPas encore d'évaluation
- Pre Calculus To Calculus Formulas)Document66 pagesPre Calculus To Calculus Formulas)Anthony Cruz100% (3)
- Conservative PDFDocument18 pagesConservative PDFAbha SrivastavaPas encore d'évaluation
- AP Calculus BC Study GuideDocument16 pagesAP Calculus BC Study GuideBrimwoodboy100% (3)
- Integrals MATH 101Document5 pagesIntegrals MATH 101Cris JacksonPas encore d'évaluation
- Unit 1 Notes PDFDocument18 pagesUnit 1 Notes PDFCharles GribbenPas encore d'évaluation
- Part Iii: Functions From R TorDocument14 pagesPart Iii: Functions From R TorTeresa Villena GonzálezPas encore d'évaluation
- Chain RuleDocument23 pagesChain RuleRaZa UmarPas encore d'évaluation
- Differential CalculusDocument6 pagesDifferential CalculusGift NathanPas encore d'évaluation
- Module 7Document18 pagesModule 7shaina sucgangPas encore d'évaluation
- Notes 20220712202310Document3 pagesNotes 20220712202310Mithal MuthammaPas encore d'évaluation
- Two-Dimensional Airfoils: 1 DefinitionsDocument5 pagesTwo-Dimensional Airfoils: 1 DefinitionsKing MassPas encore d'évaluation
- Mathematics-Ii: Prepared By: Ms. K. Rama Jyothi,: Mr. G Nagendra KumarDocument118 pagesMathematics-Ii: Prepared By: Ms. K. Rama Jyothi,: Mr. G Nagendra KumarNithya SridharPas encore d'évaluation
- Line Integral Information SheetDocument7 pagesLine Integral Information SheetRobert KoernerPas encore d'évaluation
- Cal1 Chapter 3Document80 pagesCal1 Chapter 3Vân Anh Nguyễn NgọcPas encore d'évaluation
- Some Useful Integrals of Exponential Functions: Michael FowlerDocument6 pagesSome Useful Integrals of Exponential Functions: Michael FowlerSunny HungPas encore d'évaluation
- ETH Zurich - Mechanics of Building Materials, Elastic TheoryDocument64 pagesETH Zurich - Mechanics of Building Materials, Elastic TheoryYan Naung KoPas encore d'évaluation
- Calculus of Variation and Image Processing: Scalar ProductDocument9 pagesCalculus of Variation and Image Processing: Scalar ProductAditya TatuPas encore d'évaluation
- Calculus 1 Topic 1Document9 pagesCalculus 1 Topic 1hallel jhon butacPas encore d'évaluation
- Aaaaaaa As ADocument17 pagesAaaaaaa As ANuwan SenevirathnePas encore d'évaluation
- Chapter 4 - Applications of DerivativesDocument132 pagesChapter 4 - Applications of DerivativesPhúc HồngPas encore d'évaluation
- Project in Calculus IiDocument14 pagesProject in Calculus IiBunny DummyPas encore d'évaluation
- Electricity and Magnetism NotesDocument170 pagesElectricity and Magnetism NotesUmit UtkuPas encore d'évaluation
- Applications of Derivatives: Complete Study Guide & Notes OnDocument5 pagesApplications of Derivatives: Complete Study Guide & Notes OnJuhi NeogiPas encore d'évaluation
- Differential Calculus: Engr. Denver MagtibayDocument74 pagesDifferential Calculus: Engr. Denver MagtibayViene BagsitPas encore d'évaluation
- Microproject PPT (MATHS)Document26 pagesMicroproject PPT (MATHS)BURHANUDDIN RATLAMWALAPas encore d'évaluation
- Geometry: Steven SkienaDocument22 pagesGeometry: Steven SkienapropatrioPas encore d'évaluation
- Variables or Real Multivariate Function Is A Function With More Than One Argument, With AllDocument8 pagesVariables or Real Multivariate Function Is A Function With More Than One Argument, With AllMhalyn Üü NapuliPas encore d'évaluation
- Adventures in PrecalculusDocument72 pagesAdventures in PrecalculusDr Srinivasan Nenmeli -KPas encore d'évaluation
- Geom NotesDocument10 pagesGeom NotesJ Luis MlsPas encore d'évaluation
- Viscous Fluid FlowDocument48 pagesViscous Fluid FlowTrym Erik Nielsen100% (1)
- PHYS2050 2010 2 Curl StuffDocument11 pagesPHYS2050 2010 2 Curl StuffEkky CecilPas encore d'évaluation
- Solids of Revolution Essay 1Document15 pagesSolids of Revolution Essay 1api-397091166Pas encore d'évaluation
- 2nd Sem MathDocument15 pages2nd Sem MathJayesh khachanePas encore d'évaluation
- Anna's AssignmentDocument16 pagesAnna's Assignmenttumaini murrayPas encore d'évaluation
- Derivatives 1Document25 pagesDerivatives 1Krrje IPas encore d'évaluation
- Maths PresentationDocument17 pagesMaths PresentationlshskhemaniPas encore d'évaluation
- A-level Maths Revision: Cheeky Revision ShortcutsD'EverandA-level Maths Revision: Cheeky Revision ShortcutsÉvaluation : 3.5 sur 5 étoiles3.5/5 (8)
- Ejercicios Gregory Capitulo 14Document5 pagesEjercicios Gregory Capitulo 14Gabriel BonomiPas encore d'évaluation
- BITSAT 2023 Paper Memory BasedDocument19 pagesBITSAT 2023 Paper Memory Basedkrishbhatia1503Pas encore d'évaluation
- Maletski Calculus Paper 1Document12 pagesMaletski Calculus Paper 1api-280860495Pas encore d'évaluation
- Math AA - Exploring The Method of Calculating The Surface Area of Solid of Revolution...Document22 pagesMath AA - Exploring The Method of Calculating The Surface Area of Solid of Revolution...VALENTINA GONZALEZPas encore d'évaluation
- Maths ProjectDocument26 pagesMaths Projectchaudhary.vansh2307Pas encore d'évaluation
- HSC Maths Ext1 CH2Document54 pagesHSC Maths Ext1 CH2moustafasadek11Pas encore d'évaluation
- Ga Fluid DynamicsDocument10 pagesGa Fluid DynamicsJames ChapelPas encore d'évaluation
- WKB ApproximationDocument14 pagesWKB Approximationamitsk144Pas encore d'évaluation
- Mathematical NotesDocument5 pagesMathematical NotesashPas encore d'évaluation
- Curves, Lengths, Surfaces and AreasDocument11 pagesCurves, Lengths, Surfaces and AreasRoy VeseyPas encore d'évaluation
- Limits and DerivativesDocument40 pagesLimits and DerivativesShikhin9Pas encore d'évaluation
- Executive Summary-P-5 181.450 To 222Document14 pagesExecutive Summary-P-5 181.450 To 222sat palPas encore d'évaluation
- Evs ProjectDocument19 pagesEvs ProjectSaloni KariyaPas encore d'évaluation
- PMP Assesment TestDocument17 pagesPMP Assesment Testwilliam collinsPas encore d'évaluation
- Speech On Viewing SkillsDocument1 pageSpeech On Viewing SkillsMera Largosa ManlawePas encore d'évaluation
- Science 4 Diagnostic/Achievement TestDocument5 pagesScience 4 Diagnostic/Achievement TestGe PebresPas encore d'évaluation
- Z-Purlins: Technical DocumentationDocument11 pagesZ-Purlins: Technical Documentationardit bedhiaPas encore d'évaluation
- Congenital Cardiac Disease: A Guide To Evaluation, Treatment and Anesthetic ManagementDocument87 pagesCongenital Cardiac Disease: A Guide To Evaluation, Treatment and Anesthetic ManagementJZPas encore d'évaluation
- Physics Education Thesis TopicsDocument4 pagesPhysics Education Thesis TopicsPaperWriterServicesCanada100% (2)
- Julia Dito ResumeDocument3 pagesJulia Dito Resumeapi-253713289Pas encore d'évaluation
- 40 People vs. Rafanan, Jr.Document10 pages40 People vs. Rafanan, Jr.Simeon TutaanPas encore d'évaluation
- PDFDocument10 pagesPDFerbariumPas encore d'évaluation
- An Evaluation of MGNREGA in SikkimDocument7 pagesAn Evaluation of MGNREGA in SikkimBittu SubbaPas encore d'évaluation
- India TeenagersDocument3 pagesIndia TeenagersPaul Babu ThundathilPas encore d'évaluation
- Fundaciones Con PilotesDocument48 pagesFundaciones Con PilotesReddy M.Ch.Pas encore d'évaluation
- Fire Protection in BuildingsDocument2 pagesFire Protection in BuildingsJames Carl AriesPas encore d'évaluation
- Workbook Group TheoryDocument62 pagesWorkbook Group TheoryLi NguyenPas encore d'évaluation
- Canon Powershot S50 Repair Manual (CHAPTER 4. PARTS CATALOG) PDFDocument13 pagesCanon Powershot S50 Repair Manual (CHAPTER 4. PARTS CATALOG) PDFRita CaselliPas encore d'évaluation
- Leadership Styles-Mckinsey EdDocument14 pagesLeadership Styles-Mckinsey EdcrimsengreenPas encore d'évaluation
- ML Ass 2Document6 pagesML Ass 2Santhosh Kumar PPas encore d'évaluation
- Drug Addiction Final (Term Paper)Document15 pagesDrug Addiction Final (Term Paper)Dessa Patiga IIPas encore d'évaluation
- UntitledDocument216 pagesUntitledMONICA SIERRA VICENTEPas encore d'évaluation
- Hidrl1 PDFDocument7 pagesHidrl1 PDFRajesh Kumar100% (1)
- UT Dallas Syllabus For Govt4396.002.08s Taught by Gregory Thielemann (Gregt)Document2 pagesUT Dallas Syllabus For Govt4396.002.08s Taught by Gregory Thielemann (Gregt)UT Dallas Provost's Technology GroupPas encore d'évaluation
- ECE Companies ListDocument9 pagesECE Companies ListPolaiah Geriki100% (1)
- Applications SeawaterDocument23 pagesApplications SeawaterQatar home RentPas encore d'évaluation
- Bullshit System v0.5Document40 pagesBullshit System v0.5ZolaniusPas encore d'évaluation
- Lamentation of The Old Pensioner FinalDocument17 pagesLamentation of The Old Pensioner FinalRahulPas encore d'évaluation
- Antena TelnetDocument4 pagesAntena TelnetMarco PiambaPas encore d'évaluation
- Nadee 3Document1 pageNadee 3api-595436597Pas encore d'évaluation
- TriPac EVOLUTION Operators Manual 55711 19 OP Rev. 0-06-13Document68 pagesTriPac EVOLUTION Operators Manual 55711 19 OP Rev. 0-06-13Ariel Noya100% (1)