Vectors

1 - Basic Ideas

A scalar is simply a number.

For us, this is a real number. These are things such as mass, temperature etc. (remember to use units)

A Vector is a number together with a direction.

We represent them with arrows, as this shows both direction and magnitude. Vectors are the same when they have the same direction and magnitude, no matter where there start point is, they are still equal. If we have 2 points, A & B, the straight line from A to B is a vector, denoted AB

Adding Vectors.
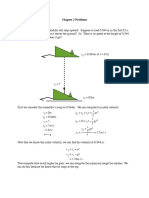
Given vector v and w we can construct the sum v+w using triangles.
V V W V+W W

Multiplying vectors by scalars.

2v has the same direction as v, but twice the length. Negative numbers reverse the direction. Notation: If v is a vector, its length is denoted |v|.

2 - Cartesian Components of vectors

We usually work with 2D & 3D cartesian coordinate grids with which to place our vectors.

j is a unit vector in y i is a unit vector in x Any other vector is a combination of these and is of the form: ai + bj where a and b are scalars

a Column vector notation. We can denote ai + bj by the column b Addition of vectors. (5i + 2j) + (3i - 7j) = (5+3)i + (2-7)j = 8i -5j OR 3 8 (5 ) + (-7) = (-5) 2 The length of a vector | ai + bj | = (a2+b2) For 3D, we use i, j & k.

()

Unit vectors.

V If we have vector v then is a direction vector of length one. This is equal to |v| V/(a2+b2+c2). This is the case unless the vector is 0i + 0j + 0k.

Position vectors If P= (x,y) is a point in 2D, and Origin = (0,0) then OP is the position vector of P. In coordinates OP is (x,y). In 3D if P=(x,y,z) then the position vector of P is x y z 3 - Scalar Product

()

Given 2 vectors, v & w the angle between them satises 0 .

Calculating
Denition

If v & w are 2 vectors, then the scalar product is dened by

v w = |v| + |w| cos where is the angle between the 2 vectors. This is a scalar quantity. Remarks: vw=wv vw=0 iff v & w are perpendicular.

IF v = (a1, a2) , w = (b1,b2) Example v= 1i + 0j

v w a1b1 + a2b2

w= 1i + 1j

Whats the angle between v & w? v w = 1= |v| + |w| cos cos = 1/2

(1 ) (1 ) = 1x1 + 1x0 = 1 1 0
= /4 = a1b1 + a2b2 + a3b3

a1 In 3D, the scalar product is a2 a3

( )( )
b1 b2 b3

Example: Whats the angle between 2i + 3j + 4k & -2i + 3j + 3k? Cos = v w / |v| |w| = -2 + 6 + 12 / (21 x 22) = 0.7312 Remark: If v = ai + bj + ck then v v = a2 + b2 + c2 |v| = (v v) v v = |v|2 cos0 = |v|2

Resolving Vectors
If is a unit vector, and v is any vector then v = |v| cos as =1, where is the angle between and v. v |v| cos So v is a component of v in the direction of .

To nd a vector perpendicular to v = 1 3 Find w so that v w = 0

()

a Set w as b and dot them = a + 3b = 0. w=

() (-3 ) 1

Vector Equations of lines and planes in 3D

Lines in 2D space that are based around an origin point. Where p and r are unit vectors of points. Some multiple of v P p r R

Origin The vector equation of the line through P and parallel to v (in the direction of v) is : r = p + tv for t If Q is any point on the line then a unique value of t gives the position vector of Q. Any real value of t describes a point on the line. If P and Q are points with position vectors p and q, then the vector equation of the line joining them, or thru P & Q, is (where r is a position vector of a point on the line) r = p + t(q-p)

Cartesian equations of lines in 3D

We need 2 different equations to dene the line in 3D space, as one on its own only denes a plane. If 2 points, P = (a1, a2, a3) & Q = (b1,b2,b3) then the line thru P&Q has the cartesian equation: x - a1 = y - a2 = z - a3 b1 - a1 b2 - a2 b3 - a3 If any point will equal zero (by b1 and a1 being the same for example) multiply up by a denominator. Example: P = (1,2,3) Q = (2,4,8) the equations are: y-2 = z-3 2 5

x-1 = y-2 2 2 x = 1/2y , y = 2/5z + 2/5 Example 2:

P = (1,2,3) Q = (1,2,5) Easy to solve because we just have to make a1 *-1 with x value x= 1 y =2

x - a1 = (b1 - a1) (z - a3) = 0 b3 - a3 y - a2 = (b2 - a2) (z - a3) = 0 b3 - a3

Vector Equation of a plane in 3D

Given a point P in 3D, and a vector n, the vector equation of the plane though P and normal to n is calculated: n RP is = r - p If R lines in the plane then r-p is perpendicular to n, so n (r - p) = 0 We know n and p so easier to write: R nr=np

If n is a unit vector then n p is the distance from the plane to the origin.

Example: n is the vector:

( ) ( )( )
1 0 -3 1 x 0 y -3 z

( )

1 0 and P is the point (1,1,0). The plane thru P, perpendicular to n is: -3 p = 1i + 1j + 1k (taken from the origin to point P).

r=1

=1

x - 3z = 1 x y z

np=1

For cartesian equation set r

()

How far is the plane from the origin? Repeat the calculation replacing n with a unit vector in the same direction: 1 = 1/10 0 -3 1 1/10 0 r = 1/10 which is the distance. -3

( ) ( )
w v

4 - Vector Product (the Cross Product)

This only works in 3D This is a vector to the normal as the 2 vectors v and w are one plane.

The vector product is v x w =

(|v| |w| sin )

If x=v, y=w then z is the normal vector. k x k = 0

vxw=-wxv If is 0 or then v x w = 0 If we use this to consider i, j & k ixi=0 jxj=0 ixj=k jxk=i kxi=j j x i = -k k x j = -i i x k = -j

The formula for nding the vector product: axb = (a2b3 - a3b2) i - (a1b3 -a3b1) j - (a1b2 - a2b1) k

(a2b3 - a3b2) (a1b3 - a3b1) (a1b2 - a2b1)