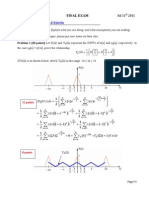
Numbers of algorithms are introduced in the IT world which is extensively used for performing the function of division in different

kinds of digital designs. All these algorithms are categorized in to two main sections. One is known as slow division while the other one is known as fast division. Both of these algorithms have their own unique working procedure through which they perform all of their tasks. Like slow division algorithm always produce just a single digit of each final quotient. Some of the famous examples of slow division algorithm are restoring and SRT. While on the other hand fast division algorithm follow the rule of closest possible approximated value relative to the finally produce quotient and produce as many digits as they can which are in twice pattern of final outcome quotient. Newton Raphson is the most famous example of fast division algorithm. Slow division algorithm, SRT division is based upon the following method of Q = N / D. In term of srt division, Q = Quotient of srt division algorithm N = Numerator (dividend) of srt division algorithm D = Denominator (divisor) of srt division algorithm Slow division methods: Basic following procedure of SRT slow division algorithm is based upon the standardized equation which is stated below: P j + 1 = R Pj qn (j + 1) D In the equation of srt slow division; Pj = partial remainder of srt division algorithm R = the radix of srt division algorithm q n-( j + 1) = the digit of the quotient in position n-(j+1), where the digit positions are numbered from 0 to n-1 in slow division srt algorithm n = number of digits in the quotient of srt division algorithm D = the denominator of srt division algorithm Restoring division: Restoring division also works on the same pattern of srt division but with some enhancements. Their operation is based upon fixed pointing value of number which are in fraction and highly depending over the following states suppositions: N<D 0 < N, D < 1 The quotient digit values of q are established with the digits starting from 0 to 1. Most basic algorithm for binary restoring division is: P:=N D : = D << n (while P and D need twice value of the word width of N and Q in srt division) for i = n-1..0 do (such as 31..0 for 32 bits) P : = 2P - D (trial subtraction is done from the shifted value of srt division) if P >= 0 then q(i) := 1 (resulting-bit value is equal to1 in srt algorithm) else q(i) := 0 (resulting bit value is 0 at this stage in srt algorithm) P : = P + D (newly achieved partial remainder is restored as a shifted value in srt algorithm) end Where as;

N = Numerator D = Denominator N = number of bits P = Partial remainder q(i) = bit number i of quotient

Several algorithms exist to perform division in digital designs. These algorithms fall into two

main categories: slow division and fast division. Slow division algorithms produce one digit of the final quotient per iteration. Examples of slow division include restoring, non-performing restoring, non-restoring, and SRT division. Fast division methods start with a close approximation to the final quotient and produce twice as many digits of the final quotient on each iteration. Newton-Raphson and Goldschmidt fall into this category. The following division methods are all based on the form Q = N / D where

Q = Quotient N = Numerator (dividend) D = Denominator (divisor).

Contents
[hide]

1 Slow division methods o 1.1 Restoring division o 1.2 Non-restoring division o 1.3 SRT division 2 Fast division methods o 2.1 NewtonRaphson division o 2.2 Goldschmidt division o 2.3 Binomial theorem 3 Large integer methods 4 Division by a constant 5 Rounding error 6 See also 7 References 8 External links

[edit] Slow division methods

Slow division methods are all based on a standard recurrence equation:

where:

Pj = the partial remainder of the division R = the radix q n-( j + 1) = the digit of the quotient in position n-(j+1), where the digit positions are numbered from least-significant 0 to most significant n-1 n = number of digits in the quotient D = the denominator.

[edit] Restoring division

Restoring division operates on fixed-point fractional numbers and depends on the following assumptions:

D<N 0 < N,D < 1.

The quotient digits q are formed from the digit set {0,1}. The basic algorithm for binary (radix 2) restoring division is:
P := N D := D << n for i = n-1..0 do P := 2P - D if P >= 0 then q(i) := 1 else q(i) := 0 P := P + D end end * P and D need twice the word width of N and Q * for example 31..0 for 32 bits * trial subtraction from shifted value * result-bit 1 * result-bit 0 * new partial remainder is (restored) shifted value

where N=Numerator, D=Denominator, n=#bits, P=Partial remainder, q(i)=bit #i of quotient

The above restoring division algorithm can avoid the restoring step by saving the shifted value 2P before the subtraction in an additional register T (i.e., T=P<<1) and copying register T to P when the result of the subtraction 2P - D is negative. Non-performing restoring division is similar to restoring division except that the value of 2*P[i] is saved, so D does not need to be added back in for the case of TP[i] 0.

[edit] Non-restoring division

Non-restoring division uses the digit set {1,1} for the quotient digits instead of {0,1}. The basic algorithm for binary (radix 2) non-restoring division is:
P[0] := N i := 0

while i < n do if P[i] >= 0 then q[n-(i+1)] := 1 P[i+1] := 2*P[i] - D else q[n-(i+1)] := -1 P[i+1] := 2*P[i] + D end if i := i + 1 end while

Following this algorithm, the quotient is in a non-standard form consisting of digits of 1 and +1. This form needs to be converted to binary to form the final quotient. Example: Convert the following quotient to the digit set {0,1}: Steps: 1. Mask the negative term: 2. Form the two's complement of N: 3. Form the positive term: 4. Sum and :

[edit] SRT division

Named for its creators (Sweeney, Robertson, and Tocher), SRT division is a popular method for division in many microprocessor implementations. SRT division is similar to non-restoring division, but it uses a lookup table based on the dividend and the divisor to determine each quotient digit. The Intel Pentium processor's infamous floating-point division bug was caused by an incorrectly coded lookup table. Five entries that were believed to be theoretically unreachable had been omitted from more than one thousand table entries.[1]

[edit] Fast division methods

[edit] NewtonRaphson division
NewtonRaphson uses Newton's method to find the reciprocal of D, and multiply that reciprocal by N to find the final quotient Q. The steps of NewtonRaphson are: 1. Calculate an estimate for the reciprocal of the divisor (D): X0. 2. Compute successively more accurate estimates of the reciprocal: 3. Compute the quotient by multiplying the dividend by the reciprocal of the divisor: Q = NXS. In order to apply Newton's method to find the reciprocal of D, it is necessary to find a function f(X) which has a zero at X = 1 / D. The obvious such function is f(X) = DX 1, but the Newton

Raphson iteration for this is unhelpful since it cannot be computed without already knowing the reciprocal of D. A function which does work is f(X) = 1 / X D, for which the NewtonRaphson iteration gives

which can be calculated from Xi using only multiplication and subtraction, or using two fused multiplyadds. If the error is defined as then

Apply a bit-shift to the divisor D to scale it so that 0.5 D 1 . The same bit-shift should be applied to the numerator N so that the quotient does not change. Then one could use a linear approximation in the form

to initialize NewtonRaphson. To minimize the maximum of the absolute value of the error of this approximation on interval [0.5,1] one should use

Using this approximation, the error of the initial value is less than

Since for this method the convergence is exactly quadratic, it follows that

steps is enough to calculate the value up to

binary places.

[edit] Goldschmidt division

Goldschmidt (after Robert Elliott Goldschmidt)[2] division uses an iterative process to repeatedly multiply both the dividend and divisor by a common factor Fi to converge the divisor, D, to 1 as the dividend, N, converges to the quotient Q:

The steps for Goldschmidt division are: 1. Generate an estimate for the multiplication factor Fi . 2. Multiply the dividend and divisor by Fi . 3. If the divisor is sufficiently close to 1, return the dividend, otherwise, loop to step 1. Assuming N/D has been scaled so that 0 < D < 1, each Fi is based on D: Fi + 1 = 2 Di. Multiplying the dividend and divisor by the factor yields:

. After a sufficient number of iterations k: Q = Nk. The Goldschmidt method is used in AMD Athlon CPUs and later models.[3][4]

[edit] Binomial theorem

The Goldschmidt method can be used with factors that allow simplifications by the Binomial theorem. Assuming N/D has been scaled by a power of two such that D = 1 x and . This yields . We choose

. Since after n steps we can round to 1 with a relative error of at most 2 n n and thus we obtain 2 binary digits precision. This algorithm is referred to as the IBM method in.[5]

[edit] Large integer methods

Methods designed for hardware implementation generally do not scale to integers with thousands or millions of decimal digits; these frequently occur, for example, in modular reductions in cryptography. For these large integers, more efficient division algorithms transform the problem to use a small number of multiplications, which can then be done using an asymptotically

efficient multiplication algorithm such as ToomCook multiplication or the SchnhageStrassen algorithm. Examples include reduction to multiplication by Newton's method as described above[6] as well as the slightly faster Barrett reduction algorithm.[7] Newton's method's is particularly efficient in scenarios where one must divide by the same divisor many times, since after the initial Newton inversion only one (truncated) multiplication is needed for each division.

[edit] Division by a constant

Division by a constant is equivalent to multiplication by its reciprocal. Since the denominator D is constant, so is its reciprocal (1 / D). Thus it is possible to compute the value of (1 / D) once at compile time, and at run time perform the multiplication / D) rather than the division (N

When doing floating point arithmetic the use of (1 / D) presents no problem. But when doing integer arithmetic it is problematic, as (1 / D) will always evaluate to zero (assuming D > 1), so it is necessary to do some manipulations to make it work. Note that it is not necessary to use (1 / D). Any value (X / Y) will work as long as it reduces to (1 / D). For example, for division by 3 the reciprocal is 1/3. So the division could be changed to multiplying by 1/3, but it could also be a multiplication by 2/6, or 3/9, or 194/582. So the desired operation of (N / D) can be changed to , where (X / Y) equals (1 / D). Although the quotient (X / Y) would still evaluate to zero, it is possible to do another adjustment and reorder the operations to produce .

This form appears to be less efficient because it involves both a multiplication and a division, but if Y is a power of two, then the division can be replaced by a fast bit shift. So the effect is to replace a division by a multiply and a shift.

There's one final obstacle to overcome - in general it is not possible to find values X and Y such that Y is a power of 2 and (X / Y) = (1 / D). But it turns out that it is not necessary for (X / Y) to be exactly equal to (1 / D) in order to get the correct final result. It is sufficient to find values for X and Y such that (X / Y) is "close enough" to (1 / D). Note that the shift operation loses information by throwing away bits. It is always possible to find values of X and Y (with Y being a power of 2) such that the error introduced by the fact that (X / Y) is only approximately equal to (1 / D) is in the bits that are discarded. For further details please see the reference.[8] As a concrete example - for 32 bit unsigned integers, division by 3 can be replaced with a multiply by . The denominator in this case is equal to 233.