Académique Documents
Professionnel Documents
Culture Documents
IPA11-E-177 Accurate Coarse Simulation Giant Gas Fields
Transféré par
delacourDescription originale:
Titre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
IPA11-E-177 Accurate Coarse Simulation Giant Gas Fields
Transféré par
delacourDroits d'auteur :
Formats disponibles
IPA11-E-177
PROCEEDINGS, INDONESIAN PETROLEUM ASSOCIATION Thirty-Fifth Annual Convention & Exhibition, May 2011 ACCURATE AND EFFICIENT COARSE-SCALE SIMULATION FOR GIANT GAS FIELDS USING TRANSMISSIBILITY-BASED UPSCALING
Toshinori Nakashima*
ABSTRACT Giant gas fields with complicated geological structures, such as faults and pinch-outs, require impractical time for fine-scale simulation for development planning and production forecasts. Therefore accurate coarse-scale simulation model is essentially required. To satisfy this requirement, we developed a new upscaling method and applied it to an actual field model. This new method is made up of two components: (1) transmissibility upscaling of fine model containing many inactive cells into a Cartesian coarse model and (2) non-Darcy flow upscaling for gas reservoirs. The developed upscaling method was tested in upscaling a fine model of 107 layers to a coarse model of 5 layers with the same areal gridding. The following results were obtained. 1) Accuracy: The resultant coarse model reproduced the production performance of the finely gridded model. On the other hand, coarse-scale models generated by conventional methods show significant errors. Speed: Time required for simulation is dramatically reduced, for example, the speed-up factor of 200 with the scale-up factor of 20.
(permeability or transmissibility). Many studies have been devoted to this research area. Review of previous studies is seen in Durlofsky (2003). One of the objectives of this paper is to upscale permeability in the complicated geometry of not only active cells but randomly penetrating inactive cells (worm-eaten shape) shown in Figure 1. Permeability upscaling method is commonly applied and available in commercial software. However, such permeability upscaling has been known to be unsuitable to complicated geometry. Transmissibility upscaling is more suitable though this method has not been paid much attention to date by some reason. The second objective of this study is to incorporate D-factor upscaling for coarse-scale flow modeling. Auriault et al.(2007), Karimi-Fard (2009), and Garibotti and Peszynska (2009) proposed upscaling approach for handling of Darcy-Forchheimer equation but no researchers have accessed the flow-dependent skin factor, which is more practical than Darcy-Forchheimer implementation since the flow-dependent factor is easier to obtain by field measurement whereas measurement of parameter in Darcy-Forchheimer equation requires special experiment. This paper proceeds as follows. We first describe upscaling parameters in this study. Numerical approach for generating calculating transmissibility and near-well parameters are then described. Subsequently application examples for an actual gas reservoir are presented and finally we show discussions and conclusions of this study. DEVELOPED METHOD Upscaling Parameters Parameters to be upscaled are grid geometry, porosity (pore volume), and permeability (transmissibility). In this paper we will focus on upscaling transmissibilities and non-Darcy effects. For porosity upscaling, we directly sum up fine pore
2)
Keyword: permeability upscaling, transmissibility upscaling, near-well upscaling, gas reservoir, flow simulation INTRODUCTION Upscaling reservoir properties in complex geometry has been a technical challenge. Our target reservoir is highly faulted giant gas field and furthermore shale is developed randomly. Such randomly developed shale has been avoiding conventional permeability upscaling towards a coarsely gridded model. For accurate reservoir simulation, upscaling is required to correctly account for complex geological features. One of the most important processes in upscaling is determination of single-phase flow parameters
* INPEX Corporation
volumes within coarse cell and provide it with reservoir simulator. Single-phase Flow Upscaling Single-phase flow upscaling methods is achieved by algebraic approach or numerical approaches. The first one uses simple averaging. This method is easy to implement and efficient but can be inaccurate. In the numerical approach, actual flow simulation is performed under specific boundary conditions. Coarse-scale flow parameter is determined by imposing Darcys law. This approach is accurate but can be inefficient. In this section, we describe procedure of upscaling tested in this study. a. Directional averaging method (DA) By considering 1D flow subject to constant pressure and no flow boundary conditions in regular-shape grids, equivalent permeability is analytically derived as arithmetic average of permeability components within the domain of interest for flow vertical to cell alignment. Harmonic average is applied to flow parallel to cell alignment. In both averaging, cell thickness is used as weighting factor. b. Flow-based permeability upscaling (FP) This approach simulates fluid flow on actual target cells. We solve following Laplace equation as:
pressure difference between the edges of the target coarse cell and L is the length of the target coarse cell for the flow direction. c. Flow-based transmissibility upscaling (TR) As transmissibility is directly incorporated with Jacobian matrix to be handled in reservoir simulation, accurate determination of coarse-scale transmissibility is expected to enable accurate coarse-scale flow modeling. Unlike permeability, transmissibility can account for inter-cell flow across a fault where usual connection such as (I,J,K) to (I+1,J,K) no longer occurs due to distance shift along a fault plane. The procedure of TR is similar to the numerical permeability upscaling. The domain corresponding to two coarse cells is extracted and fine-scale flow simulation is performed. Pressure solution of Eq. 1 in fine-scale is used to determine coarse-scale transmissibility as:
T* =
q p1 p0
,
(3)
where T * is coarse-scale transmissibility. p j
q are average pressure over fine cells corresponding to coarse cell j and total flow
and rate over fine cells composing coarse-cell interface as:
( k p ) = 0
(1)
p PV p= PV
i i i i
in the domain in fine-scale corresponding to the target coarse cell of interest. Boundary conditions are applied to impose a directional flow. In this study constant pressure for the direction of interest and no-flow boundary conditions for others are applied. The upscaled permeability k * is calculated as:
q = qi
i
(4)
(5)
pi is fine-scale pressure solution, PVi is fine cell pore volume, qi is fine-scale flow rate at
the interface calculated from pressure solution and Darcys law. This calculation is implemented for all x, y, and z flow directions. Transmissibility for non-neighbor connections is computed by similar way. In the numerical permeability and transmissibility approaches, additional region, skin, around target coarse cell can be
k* =
L q Ap
(2)
where A is average cross-sectional area of the face vertical to the flow direction, p is
incorporated with flow simulation in fine-scale for alleviating influences of the imposed boundary conditions. We define the size of the skin using the number of fine rings surrounding the target coarse cell. We represent this quantity by r. For example, r = 0 means no additional region. Figure 2 shows the domain and boundary conditions for the transmissibility upscaling. This figure presents the case of r = 2. To consider flows through faults, this has to be introduced since there are flows between different layers. d. Near-well upscaling In near-well region, flow forms radial pressure distribution, which has to be incorporated with upscaling procedure. Our computation follows Ding (1995). In the upscaling calculation, fine grids corresponding to coarse well block and surrounding coarse blocks is extracted and then radial flow is simulated on fine-scale model by imposing pressure boundary conditions (Figure 3). The solution is use to compute coarse-scale well * * index WI and transmissibilities Tw between well-block and adjacent coarse blocks are computed as:
q=
2 kh r ln 0 + S + D q rw
( p0 pw )
(8)
where rw is wellbore radius, r0 is effective wellbore radius, S is mechanical skin factor of the well, and D is non-Darcy skin coefficient (D-factor): In general the value of D-factor ranges order of 10-4 to 10-3 day/Mscf in field unit system. D-factor should be given to each cell in flow simulation but generally it is difficult to estimate completion D-factor by field measurement therefore one D-factor value is given not for each completion but for one well. Completion D-factor D j is converted from well D-factor in reservoir simulator. We consider directly providing a cell a D-factor to coarse-scale simulation. Solving Eq. 8 with respect to D and imposing the agreement of free gas flow rate between fine and coarse-scale models, a D-factor for each coarse-grid completion can be determined as:
WI * =
* Tw =
qw p0 pw
(6)
q p1 p0
qw
and (7)
D* = j
a j q j WI j p j pw q2 j
)
(9)
where
are the well flow rate
where a j is represented as:
from fine cells belonging to the coarse grid of interest and flow rate at the interface between coarse well block and neighboring block. e. Non-Darcy flow effect In a velocity flow regime faster than industrial criteria, Darcys law is no longer applicable. Non-Darcy flow is rigorously described by Darcy-Forchheimer equation, which has to be solved over entire reservoir model instead of the standard Darcy flow equation. A region causing non-Darcy flow, however, is generally limited only to near-well region where fluid rapidly flows. Therefore we use a rate-dependent skin factor to represent non-Darcy flow. By considering radial form, the Darcy-Forchheimer equation can be reduced to:
a j = ln ( r0 rw ) + S
(10) Eq. 9 and 10 are used for the D-factor upscaling. For more accuracy, optimization approach can be introduced by setting the objective function to be minimized as the difference of fine and coarse well flow rates. This enables to simultaneously * * determine Darcy flow parameters ( WI , Tw ) and non-Darcy flow parameters, D * . f. Handling of worm-eaten shape One of the difficulties in upscaling our geological model is warm-eaten shape that many
inactive cells are randomly distributed. These inactive cells have a considerable volume and it has some impact on fluid flow. In the context of mathematics, a system of equations, which is derived from the Laplace equation for local domains involving isolated active cells from other active cells, cannot be mathematically solved. Figure 4 shows finite-difference based matrix to be solved for the pressure solution. Nonzero elements only for cell 1 and 2 in Figure 2, which are disconnected with other cells, are shown in the matrix. T in the matrix denotes transmissibility between those cells. We see that these elements are completely same if we multiply by -1 to those of cell 1 or 2. This means that the matrix is singular. It is common to apply a heuristic approach that provides low permeability value (e.g. ~10-6 mD) to regard them as active and solves the standard system of equation. The number of unknowns to be solved, however, is increased as original inactive cells becomes active and trial and error is required to find the appropriate value of the low permeability (If we provide too small permeability value, the matrix becomes nearly singular. In case of too large value, the solution is inaccurate because the system is influenced by the provided value). In this study, we consider introducing slight rock compressibility (e.g. ~10-9 1/psi) to the system without making inactive cells active. Hence we solve the following slightly compressible single-phase flow equation as:
CASE STUDY Fine Model Description The developed upscaling method was tested against a real gas reservoir with the average permeability and porosity of 140 mD and 10 %, respectively. 22 vertical wells exist as producer. This reservoir consists of two portions irregularly developed each other like worm-eaten shape, a productive portion and unproductive portion. Variograms are modeled with the range of 5 km 3 km for the horizontal direction and 5 m for the vertical direction and thus is used for porosity and permeability modeling. The grid dimension is 400 m square with various thickness. The total number of grid is 173 144 107 (~2.7 million) including non-productive cells (inactive cells). The permeability field is fairly heterogeneous and there are many faults and pinch-out. Reservoir fluid is wet gas where the dew point pressure is far above the initial reservoir pressure. The reservoir is geologically divided into five zones, A, B, C, D, and E from top to bottom. Figure 6 shows permeability field and well locations of the target reservoir. Implementation of Upscaling Three upscaling approaches, permeability upscaling (averaging and numerical) and transmissibility upscaling, are tested to demonstrate the accuracy and efficiency of the transmissibility upscaling. For the permeability upscaling, commercial modeling software is used. We developed in-house transmissibility upscaling program and applied it to our geological model. For numerical upscaling (both permeability and transmissibility), three fine-scale rings around target domain are used as skin region. Full-field Simulation Results We now describe the results of coarse-scale simulation. In the upscaling, areal resolution is unchanged since the grid size is large enough. Therefore upgridding only for layers is applied based on the geological zones. Coarse-scale layering is decided by a geologist honoring the geological features. Table 1 shows geological zone and relation between fine and coarse layers. As shown in the table we prepare two coarse-scale models (29-layer and 5-layer models).
( k p ) = V
. t
(11)
This enables to avoid singular matrix due to additional term to diagonal elements of the matrix. Figure 5 represents this. As A is added to diagonal elements of the matrix, it should not be singular. Though a few iterations for handling its nonlinearity and several time-step iterations for making flow steady-state are required, number of unknowns are kept as that of active cells and no trial and error is needed. This leads to much faster upscaling than the heuristic approaches. Comparison of required time for both cases will be mentioned in the following chapter.
Full field simulation is performed using black oil reservoir simulator. To see the effects of single-phase upscaling, we set minimum well flowing pressure is set above dew point pressure with maximum gas flow rate of 100 MMscf/day and make water immovable by manipulating critical water saturation. First non-Darcy flow effect is not set (D-factor set zero) and the second run uses D-factor of 5x10-4 day/Mscf. The duration of the simulation period is 30 years. Darcy Flow Upscaling We next demonstrate the effects of Darcy flow upscaling. Figure 7 (29-layer model) and Figure 8 (5-layer model) show well flowing pressure and gas production rate of Well 9 that shows most drastic difference. Non-Darcy flow effect is not incorporated yet. We see perfect agreement of the in-house transmissibility based (TR) coarse simulation results with the reference fine model. On the other hand, the two permeability-based coarse models show significantly different production performance. For example, plateau production period is 7000 days and 5500 days for directional averaging (DA) and flow-based permeability (FP) while the reference fine model continues 2100 days plateau gas production. Other 21 wells also show same trend observed here. Figure 9 and 10 show well by well drawdown error at 1872 days for 29-layer and 5-layer coarse-scale model. The definition of the error here is:
Efficiency comparison among different upscaling procedure will be discussed in the following chapter. Non-Darcy Flow Upscaling Here simulation results incorporating non-Darcy flow effects are demonstrated. Figure 11 and Figure 12 show flowing pressure and gas production rate of Well 17 and Well 22 of 5-layer model (here best and worst well in terms of draw down error are shown). For the comparison purpose, Darcy flow case is also shown. We see that non-Darcy flow effects decrease the duration of the plateau gas production 2000-4000 days for all wells. TR coarse-scale model shows good agreement with the reference fine model. Although not shown here, the accuracy of the two permeability-based coarse models (DA and FP) are poor as we saw in the Darcy flow case. Figure 13 shows error (defined as Eq. 12) of well pressure at 1927 days. Average error in this case is 1.6 % over 22 wells for TR model (41 % in DA and 25.6 % in FP). It is obvious that suggested upscaling approach for D-factor correctly computes the coarse-scale parameter DISCUSSION In this paper, advantage of transmissibility upscaling approach is demonstrated using actual full field simulation. Significant improvement of accuracy in well production performance and considerable errors in predicting bottomhole pressure compared with algebraic and numerical permeability upscaling are presented. The case study presented here uses the actual gas reservoir model. Upscaling only in the vertical direction is commonly applied and single-phase flow parameters are inevitable to upscale for building coarse-scale model for efficient flow simulation. Therefore the observations demonstrated in this paper would be expected to be applicable to similar problems as our problem is never rare case. Permeability upscaling causes one or two inconsistencies between fine and coarse-scale model in our case. The first inconsistency occurs in the permeability averaging. Since the equivalent permeability formulation is derived subject to specific conditions (regular hexahedron shape of grid, constant pressure drop for flow direction with no flow elsewhere), geological model consisting of distorted cells and sometimes pentahedron (due to
Error [ %] =
coarse fine pw pw fine pinitial pw
100
.
(12)
According to the figures, TR is the best approach which provides less 6 % of error (1.5 % in average over 22 wells for both 29-layer and 5-layer model), the second best is FP (8.6 % for 29-layer and 25.8 % for 5-layer model in average), and DA is the worst (26.2 % for 29-layer and 39.4 % error for 5-layer model). Error in TR is independent of scaleup factor while permeability-based model (DA and FP) increases the error as the scaleup factor increases. In the context of efficiency in handling worm-shape, proposed method in Sec. 2.7 is much faster than the heuristic approach. This is because number of unknowns to be solved in each coarse transmissibility computation. Additionally, number of coarse-scale transmissibility is also smaller since many of coarse cells consist of only inactive cells.
pinch-out) is not suitable for the averaging approach. The second inconsistency is caused by the default setting of commercial flow simulators. Once we provide permeability with coarse-scale model, the flow simulator internally converts it to transmissibility. In the process, there is no consideration of actual fine-scale flow between coarse cells, which has to be incorporated in the conversion process from permeability to transmissibility. This is especially significant in highly faulted reservoirs. In the transmissibility upscaling, above inconsistencies are removed because 1) fine-scale inter-cell flow is simulated using actual target model and 2) upscaled transmissibility is directly provided with flow simulator. These are the reason that transmissibility-based model shows significantly better simulation results. The presence of worm-eaten shape in the geological model deteriorates coarse-scale simulation with upscaled permeability. We now consider two adjacent coarse cells. In case one of two fine cells in different coarse cells geometrically connected is inactive in all layers, all transmissibilities in each layer are zero. This means the interface between the cells is impermeable. However, if permeability upscaling is applied, the coarse cells have nonzero permeability and this results in nonzero coarse-scale transmissibility. The longer plateau production for permeability-based coarse model demonstrated in this paper is caused by this. Transmissibility upscaling enables to avoid this problem as the approach can consider cell to cell connections in fine-scale. This also supports the use of transmissibility upscaling. Another important aspect of upscaling is the required CPU time for upscaling and coarse-scale flow simulation. In the context of timing of upscaling and simulation, transmissibility upscaling is disadvantageous compared with the permeability upscaling due to larger number of grid blocks used in pressure solution. The required CPU time for the transmissibility upscaling is more than ten times of directional averaging and nearly three times of numerical permeability computation for the 5-layer model case (For 29-layer model the difference is much smaller because the pressure solution does not consume CPU time). In a practical sense, however, once coarse-scale transmissibility is determined we need no upscaling
calculation again until geological model is updated. Actual speed-up factors (defined as the ratio of CPU time for fine-scale simulation to CPU time for coarse-scale simulation) are 85 for 29-layer model and 212 for 5-layer model. This speed-up is desired in multiphase upscaling and it is expected that the upscaling contributes the reduction of performance prediction and optimization of reservoir development plan. In this study, r = 3 (r is defined in Sec. 2.3.1) is used as additional region for local fine simulation for both permeability and transmissibility upscaling. No sensitivity is not investigated the effect of fine ring size to accuracy and efficiency. There is room to improve the efficiency of upscaling calculation.
CONCLUSIONS In this study, we obtained the following conclusions: 1) Permeability (directional averaging and flow-based) and transmissibility (flow-based) are compared for single-phase coarse-scale full field flow simulation. Transmissibility-based coarse model is demonstrated to be more accurate than permeability upscaling approaches by showing well performances. 2) An approach for non-Darcy D-factor upscaling is presented and the accuracy of upscaled D-factor is presented.
3) Numerical problem caused by worm-eaten shape in the geological model is resolved by proposed method, which introduces slight compressibility in fine-scale pressure solution. Inaccuracy in coarse-scale simulation caused by the feature is resolved by transmissibility upscaling. 4) Simulation time is dramatically improved with speed-up factor of 85 for 29-layer model and 212 for 5-layer model. ACKNOWLEDGEMENT The author would like to thank INPEX Corporation for permission of presenting this paper. REFERENCE Auriault, J.-L., Geindreau, C., and Oregas, L., 2007, Upscaling Forchheimer law: Transport in Porous Media, 70(2), 213-229
Ding, Y., 1995, Scaling-up in the vicinity of wells in heterogeneous field: SPE29137 presented at 13th SPE Symposium on Reservoir Simulation
Garibotti, C.R. and Peszynska, M., 2009, Upscaling non-Darcy flow: Transport in Porous Media. 80(3), 401-430 Karimi-Fard, M. and Durlofsky, L.J., 2009, Detailed near-well Darcy-Forchheimer flow modeling and upscaling on unstructured 3D grids: SPE 118999 presented at the SPE Reservoir Simulation Symposium
Durlofsky, L.J., 2003, Upscaling of geocellular models for reservoir flow simulation: A review of recent progress: paper presented at 7th International Forum on Reservoir Simulation
TABLE 1 COARSE LAYERING (TOP: 29-LAYER MODEL, BOTTOM: 5-LAYER MODEL)
Figure 1 - Many inactive cells (example in layer 65): Color shows permeability. Blanc parts represent inactive cells.
Figure 2 - Schematic of flow-based transmissibility upscaling: Bold lines show coarse cell and thin lines show fine cell. Black grid denotes inactive cell. p j is average pressure in coarse cell j. q is integrated flow rate across the target interface of coarse cells. 1 and 2 are referred cell as the difficulty of handling of isolated active cell.
Figure 3 - Schematic of near-well upscaling: Black circle in center is well. Bold lines show coarse cell and thin lines show fine cell. p j is average pressure in coarse cell j. q from the well. is integrated flow rate
Figure 4 - Matrix of finite-difference flow equation: T denotes transmissibility between two fine cells of 1 and 2described in Figure 2.
Figure 5 - Modified matrix of finite-difference flow equation: T denotes transmissibility between two fine cells of 1 and 2described in Figure 2. Aj denotes additional term by introducing compressibility into the system.
Figure 6 -
Permeability field of target reservoir: Color shows permeability. Legend is shown at the bottom. Well locations are shown as vertical lines (concentrated on upper right part in this figure). Note that vertical scale is exaggerated 30 times.
Figure 7 - Comparison of well pressure and gas rate (29-layer model)
Figure 8 - Comparison of well pressure and gas rate (5-layer model)
Figure 9 - Error of well pressure at 1872 days (29-layer model)
Figure 10 - Error of well pressure at 1872 days (5-layer model)
Figure 11 - Well pressure and gas rate of Well 17 with/without non-Darcy flow effect
Figure 12 - Well pressure and gas rate of Well 22 with/without non-Darcy flow effect
Figure 13 - Error of well pressure at 1927 days (5-layer model)
Vous aimerez peut-être aussi
- Streamline Simulation Waterflood StanfordDocument8 pagesStreamline Simulation Waterflood Stanfordpetro121Pas encore d'évaluation
- Simulation Study of Mass Transfer Coefficient in Slurry Bubble Column Reactor Using Neural NetworkDocument11 pagesSimulation Study of Mass Transfer Coefficient in Slurry Bubble Column Reactor Using Neural NetworkEmad ElsaidPas encore d'évaluation
- CFD Mini ProjectDocument11 pagesCFD Mini ProjectSujay PrabhatPas encore d'évaluation
- Creeping Flow in Two-Dimensional Network - 1982Document29 pagesCreeping Flow in Two-Dimensional Network - 1982Alireza Attari MPas encore d'évaluation
- 2004 POF Xu MartinDocument17 pages2004 POF Xu MartinKhan ABPas encore d'évaluation
- Ying 2011 A PDFDocument6 pagesYing 2011 A PDFAngel CerriteñoPas encore d'évaluation
- 456Document21 pages456David LapacaPas encore d'évaluation
- Example-Steady Incompressible Flow: Solved With Comsol Multiphysics 3.5ADocument14 pagesExample-Steady Incompressible Flow: Solved With Comsol Multiphysics 3.5AGabotecnaPas encore d'évaluation
- Comparison of the Effects of k-, k-ω, and Zero Equation Models on Characterization of Turbulent Permeability of Porous MediaDocument8 pagesComparison of the Effects of k-, k-ω, and Zero Equation Models on Characterization of Turbulent Permeability of Porous MediaGanesh GPPas encore d'évaluation
- Flow over ogee spillway analysisDocument26 pagesFlow over ogee spillway analysisharsh agarwalPas encore d'évaluation
- 2015 - Calibration of An Air Entrainment Model For CFD Spillway ApplicationsDocument12 pages2015 - Calibration of An Air Entrainment Model For CFD Spillway ApplicationsYen Kun HoPas encore d'évaluation
- Boundary Element Technique in Petroleum Reservoir SimulationDocument8 pagesBoundary Element Technique in Petroleum Reservoir Simulationiky77Pas encore d'évaluation
- Numerical modelling of subcritical open channel flowDocument7 pagesNumerical modelling of subcritical open channel flowchrissbansPas encore d'évaluation
- A Finite-Volume Algorithm For All Speed FlowsDocument8 pagesA Finite-Volume Algorithm For All Speed Flowsles_lesPas encore d'évaluation
- Numerical Simulation of A Synthetic Jet Actuator: Icas 2000 CongressDocument9 pagesNumerical Simulation of A Synthetic Jet Actuator: Icas 2000 CongressYeong Leong LimPas encore d'évaluation
- Flow Configurations in A Lid Driven Cavity With Throughflow: A. Dragomirescu, N. Alleborn, H. Raszillier, and F. DurstDocument27 pagesFlow Configurations in A Lid Driven Cavity With Throughflow: A. Dragomirescu, N. Alleborn, H. Raszillier, and F. DurstDragomirescu AndreiPas encore d'évaluation
- CFD Analysis of Backward-Facing Step FlowDocument16 pagesCFD Analysis of Backward-Facing Step FlowsssssPas encore d'évaluation
- Flow Modeling Based Wall Element TechniqueDocument8 pagesFlow Modeling Based Wall Element TechniqueAI Coordinator - CSC JournalsPas encore d'évaluation
- Steady-State and Unsteady-State Flow of Non':'Newtonian Fluids Through Porous MediaDocument9 pagesSteady-State and Unsteady-State Flow of Non':'Newtonian Fluids Through Porous Mediazulike2004Pas encore d'évaluation
- Transonic Potential Flow Calculations by Two Artificial Density MethodsDocument5 pagesTransonic Potential Flow Calculations by Two Artificial Density MethodsJonathanPas encore d'évaluation
- Accuracy of Viscous Resistance Computations For Ships Including Free Surface EffectsDocument4 pagesAccuracy of Viscous Resistance Computations For Ships Including Free Surface Effectsabjm5822Pas encore d'évaluation
- Report of Fluent Simulation of Aerofoil NACA 4412Document19 pagesReport of Fluent Simulation of Aerofoil NACA 4412احمد عبد المحمود100% (3)
- Rapid Crack Propagation in Plastic Pipe: Predicting Full-Scale Critical Pressure From S4 Test ResultsDocument16 pagesRapid Crack Propagation in Plastic Pipe: Predicting Full-Scale Critical Pressure From S4 Test ResultsE.s. BinbillahPas encore d'évaluation
- Energies: An Investigation of Parallel Post-Laminar Flow Through Coarse Granular Porous Media With The Wilkins EquationDocument19 pagesEnergies: An Investigation of Parallel Post-Laminar Flow Through Coarse Granular Porous Media With The Wilkins EquationNasser93Pas encore d'évaluation
- Modeling VVER Reactor Pressure Vessel CFDDocument9 pagesModeling VVER Reactor Pressure Vessel CFDlovehurt1386Pas encore d'évaluation
- Flow Over A CylinderDocument14 pagesFlow Over A CylinderHariVathsalaPas encore d'évaluation
- Spreadsheet Evaluation of Slug TestsDocument14 pagesSpreadsheet Evaluation of Slug TestsAdly Al-SaafinPas encore d'évaluation
- ZACM4921 HypersonicsDocument9 pagesZACM4921 HypersonicsChowkidar KarthikPas encore d'évaluation
- Ha Midi Pour AbstractDocument2 pagesHa Midi Pour Abstracthhqq2010Pas encore d'évaluation
- DNS lowREDocument8 pagesDNS lowREPratzen HillPas encore d'évaluation
- Numerical Study of Gas-Solid Flow in A Cyclone Separator: B. Wang, D. L. Xu, G. X. Xiao, K. W. Chu and A. B. YUDocument6 pagesNumerical Study of Gas-Solid Flow in A Cyclone Separator: B. Wang, D. L. Xu, G. X. Xiao, K. W. Chu and A. B. YUAzharuddin Ehtesham FarooquiPas encore d'évaluation
- Simulation of Synthetic Jets in Quiescent Air Using Unsteady Reynolds Averaged Navier-Stokes EquationsDocument17 pagesSimulation of Synthetic Jets in Quiescent Air Using Unsteady Reynolds Averaged Navier-Stokes EquationsSebastian Cano CampuzanoPas encore d'évaluation
- Numerical Study of Wall Shear and Velocities Using A Commercial CFD Code: Some Crucial Aspects To ConsiderDocument5 pagesNumerical Study of Wall Shear and Velocities Using A Commercial CFD Code: Some Crucial Aspects To ConsiderİLKER İNANPas encore d'évaluation
- Ifasd 074Document16 pagesIfasd 074Rafa PalaciosPas encore d'évaluation
- Upscaling of Relative Permeability Using Pseudo Functions: A. Hashemi, S. R. Shadizadeh, and G. ZargarDocument11 pagesUpscaling of Relative Permeability Using Pseudo Functions: A. Hashemi, S. R. Shadizadeh, and G. Zargarsajjad moradiPas encore d'évaluation
- Numerical Simulation of Turbulent Flow Through A Francis Turbine RunnerDocument6 pagesNumerical Simulation of Turbulent Flow Through A Francis Turbine RunnerAngel CerriteñoPas encore d'évaluation
- Reverse Step FlowDocument11 pagesReverse Step FlowRupesh BhusalPas encore d'évaluation
- Spe 55225 ProductivityindezgasDocument10 pagesSpe 55225 ProductivityindezgasJose Gregorio Fariñas GagoPas encore d'évaluation
- ADMOS 2013 conference paper on fully coupled finite volume solverDocument12 pagesADMOS 2013 conference paper on fully coupled finite volume solverErnesto Delfino AguirrePas encore d'évaluation
- Derivation of Adjoint Drift Flux EquationsDocument21 pagesDerivation of Adjoint Drift Flux Equationsbendel_boyPas encore d'évaluation
- Validation of The Volume of Fluid Method For Free Surface Calculation: The Broad-Crested WeirDocument11 pagesValidation of The Volume of Fluid Method For Free Surface Calculation: The Broad-Crested WeirSandra PowersPas encore d'évaluation
- Ijms 47 (1) 89-95Document7 pagesIjms 47 (1) 89-95Gaming news tadkaPas encore d'évaluation
- Discontinuous Galerkin Methods For Flow and Transport Problems in Porous MediaDocument6 pagesDiscontinuous Galerkin Methods For Flow and Transport Problems in Porous MediaRamesh JangalaPas encore d'évaluation
- Experimental Study of Flow About A Square Cylinder Placed On A WallDocument4 pagesExperimental Study of Flow About A Square Cylinder Placed On A Wallxikun WPas encore d'évaluation
- CFD Simulations of Lid Driven Cavity Flow at Moderate Reynolds NumberDocument14 pagesCFD Simulations of Lid Driven Cavity Flow at Moderate Reynolds NumberVivek JoshiPas encore d'évaluation
- Solution of Transient Transport Equation Using An Upstream Finite Element SchemeDocument11 pagesSolution of Transient Transport Equation Using An Upstream Finite Element SchemechrissbansPas encore d'évaluation
- Numerical Simulation of Flow Past A Circular Cylinder With Varying Tunnel Height To Cylinder Diameter at Re 40Document7 pagesNumerical Simulation of Flow Past A Circular Cylinder With Varying Tunnel Height To Cylinder Diameter at Re 40International Journal of computational Engineering research (IJCER)Pas encore d'évaluation
- Flow Around A Circular Cylinder With Fluent: Mech/Chbi 301 Fluid MechanicsDocument14 pagesFlow Around A Circular Cylinder With Fluent: Mech/Chbi 301 Fluid Mechanicsnidhul07Pas encore d'évaluation
- Investigación NavierDocument10 pagesInvestigación NavierIVONNE PATRICIA YANA ENRIQUEZPas encore d'évaluation
- Chemical Engineering ScienceDocument7 pagesChemical Engineering ScienceclaudiosldfPas encore d'évaluation
- New algorithm estimates three-phase relative permeability from core experimentsDocument6 pagesNew algorithm estimates three-phase relative permeability from core experimentsRosa K Chang HPas encore d'évaluation
- Investigation of A Mixing Length and A Two-Equation Turbulence Model Utilizing The Finite Element MethodDocument6 pagesInvestigation of A Mixing Length and A Two-Equation Turbulence Model Utilizing The Finite Element MethodchrissbansPas encore d'évaluation
- Persamaan WigginsDocument2 pagesPersamaan WigginsDjohan Pranata KabanPas encore d'évaluation
- " - Si, - P-Z: Convergence Criteria For Iterative ProcessesDocument2 pages" - Si, - P-Z: Convergence Criteria For Iterative ProcessesKtk ZadPas encore d'évaluation
- A New Mathematical Model For Coandă Effect Velocity ApproximationDocument8 pagesA New Mathematical Model For Coandă Effect Velocity ApproximationValeriu DraganPas encore d'évaluation
- Important ThroughflowDocument14 pagesImportant ThroughflowkoolwaveoceanicPas encore d'évaluation
- Y. F. Yao and N. D. Sandham - Direct Numerical Simulation of Turbulent Trailing-Edge Flow With Base Flow ControlDocument9 pagesY. F. Yao and N. D. Sandham - Direct Numerical Simulation of Turbulent Trailing-Edge Flow With Base Flow ControlWhiteLightePas encore d'évaluation
- 4th High Performance Yacht Design Conference hydrodynamic performanceDocument8 pages4th High Performance Yacht Design Conference hydrodynamic performancemsimran11Pas encore d'évaluation
- Parallel Computational Fluid Dynamics 2002: New Frontiers and Multi-Disciplinary ApplicationsD'EverandParallel Computational Fluid Dynamics 2002: New Frontiers and Multi-Disciplinary ApplicationsPas encore d'évaluation
- Parallel Computational Fluid Dynamics 2001, Practice and TheoryD'EverandParallel Computational Fluid Dynamics 2001, Practice and TheoryP. WildersPas encore d'évaluation
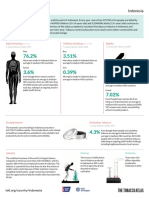
- Tobacco Companies Market ShareDocument1 pageTobacco Companies Market ShareIndonesia TobaccoPas encore d'évaluation
- Seismic InversionDocument22 pagesSeismic InversionStavrosVrachliotisPas encore d'évaluation
- Indonesia Country FactsDocument2 pagesIndonesia Country FactsdelacourPas encore d'évaluation
- iBT/Next Generation TOEFL Test: Integrated Writing Rubrics (Scoring Standards)Document0 pageiBT/Next Generation TOEFL Test: Integrated Writing Rubrics (Scoring Standards)Osama AldahamshehPas encore d'évaluation
- Fall Cycle Online Application and Credential DeadlinesDocument1 pageFall Cycle Online Application and Credential DeadlinesdelacourPas encore d'évaluation
- Seismic Stratigraphy - Methodology ExxonDocument29 pagesSeismic Stratigraphy - Methodology ExxonSimona Murarita100% (1)
- Cap3 Seismic StratigraphyDocument16 pagesCap3 Seismic StratigraphydelacourPas encore d'évaluation
- Toplap (Figure 4.22) - An Analogue To This Is A Perfect Set of Cross-Stratified BedsDocument2 pagesToplap (Figure 4.22) - An Analogue To This Is A Perfect Set of Cross-Stratified BedsdelacourPas encore d'évaluation
- TopicDocument8 pagesTopicdelacourPas encore d'évaluation
- Ipa11 G 194Document10 pagesIpa11 G 194delacourPas encore d'évaluation
- Workflow of Seismic Data AnalysisDocument5 pagesWorkflow of Seismic Data AnalysisdelacourPas encore d'évaluation
- Java Petroleum GeologyDocument54 pagesJava Petroleum Geologydelacour100% (1)
- NST Mmii Chapter3Document18 pagesNST Mmii Chapter3Faisal RahmanPas encore d'évaluation
- Rock physics analysis reveals reservoir characteristics of calcitic-dolomitic sandstoneDocument14 pagesRock physics analysis reveals reservoir characteristics of calcitic-dolomitic sandstonedelacourPas encore d'évaluation
- Rock physics analysis reveals reservoir characteristics of calcitic-dolomitic sandstoneDocument14 pagesRock physics analysis reveals reservoir characteristics of calcitic-dolomitic sandstonedelacourPas encore d'évaluation
- Seismic InterpretationDocument9 pagesSeismic InterpretationdelacourPas encore d'évaluation
- Ipa11 e 024Document15 pagesIpa11 e 024delacourPas encore d'évaluation
- Ipa11 G 194Document10 pagesIpa11 G 194delacourPas encore d'évaluation
- Ipa11 e 024Document15 pagesIpa11 e 024delacourPas encore d'évaluation
- Application of Elctric MethodDocument15 pagesApplication of Elctric MethoddelacourPas encore d'évaluation
- 3 D Geologic Model AttributeDocument8 pages3 D Geologic Model AttributedelacourPas encore d'évaluation
- 3 D Geologic Model AttributeDocument8 pages3 D Geologic Model AttributedelacourPas encore d'évaluation
- Trepel Challenger 700Document2 pagesTrepel Challenger 700ZoranPas encore d'évaluation
- Prosedur uji bantalan betonDocument2 pagesProsedur uji bantalan betonArie SaiyukiPas encore d'évaluation
- Astm E11-16Document11 pagesAstm E11-16Said MohamedPas encore d'évaluation
- Ref: LOA No. IRCON/ELECT/2067/KG/TENDER/OHE&PSI/PKG-I/01/263 Dated 09.04.2018Document2 pagesRef: LOA No. IRCON/ELECT/2067/KG/TENDER/OHE&PSI/PKG-I/01/263 Dated 09.04.2018ShasheekantPas encore d'évaluation
- Bosch P-Pump Fuel Injection - Diesel Tech - Diesel Power MagazineDocument2 pagesBosch P-Pump Fuel Injection - Diesel Tech - Diesel Power Magazinerxhughes100% (3)
- Topographic Map of NorwoodDocument1 pageTopographic Map of NorwoodHistoricalMapsPas encore d'évaluation
- Me PPT About SSCMDocument18 pagesMe PPT About SSCMSana SaleemPas encore d'évaluation
- Data Sheet For Actuators For On-Off Valves: OctoberDocument13 pagesData Sheet For Actuators For On-Off Valves: OctoberFershaalPas encore d'évaluation
- JAR 66 Module 1 Propeller Exam PracticeDocument43 pagesJAR 66 Module 1 Propeller Exam Practicerobija1Pas encore d'évaluation
- Application Answers:: Dual-Gradient DrillingDocument4 pagesApplication Answers:: Dual-Gradient Drillinglich_tran01Pas encore d'évaluation
- Universal Grade Strandvise MacleanDocument1 pageUniversal Grade Strandvise MacleanLuis Manuel Montoya RiveraPas encore d'évaluation
- DX200 MML CommandDocument3 pagesDX200 MML Commanddedeputra01Pas encore d'évaluation
- Construction Safety Inspection ChecklistDocument2 pagesConstruction Safety Inspection ChecklistDisenyo Arkitekto100% (1)
- 09931372A Clarus 590 User's GuideDocument284 pages09931372A Clarus 590 User's GuideLuz Idalia Ibarra RodriguezPas encore d'évaluation
- Water Leak Detection System Riser Diagram-Al Shamal-Rev00Document1 pageWater Leak Detection System Riser Diagram-Al Shamal-Rev00Don Roseller DumayaPas encore d'évaluation
- U3W4 KeyDocument2 pagesU3W4 KeyAndrew Turner50% (2)
- CT Basics and Applications For StudentDocument230 pagesCT Basics and Applications For Studentanon_969492799Pas encore d'évaluation
- One, Two, Rotational Kinematics (Review)Document3 pagesOne, Two, Rotational Kinematics (Review)Music LastPas encore d'évaluation
- CS C372/IS C362 - Operating System: Birla Institute of Technology & Science, Pilani QUIZ 2 - Closed BookDocument2 pagesCS C372/IS C362 - Operating System: Birla Institute of Technology & Science, Pilani QUIZ 2 - Closed BookVishal MittalPas encore d'évaluation
- Week 6 (Study Guide Exercise) - Lukita Yuviananda - 02411840000064Document8 pagesWeek 6 (Study Guide Exercise) - Lukita Yuviananda - 02411840000064Lukita YuvianandaPas encore d'évaluation
- Economics of Power GenerationDocument22 pagesEconomics of Power Generationbhaskar123321Pas encore d'évaluation
- VG7 Maintenance ManualDocument18 pagesVG7 Maintenance ManualGustavo RodriguezPas encore d'évaluation
- Android Smartphone Adoption and Intention To Pay For Mobile InternetDocument20 pagesAndroid Smartphone Adoption and Intention To Pay For Mobile InternetradislamyPas encore d'évaluation
- Threshold Logic SeminarDocument20 pagesThreshold Logic SeminarAkash HulkodPas encore d'évaluation
- Contoh Perhitungan Lifting Set Dan PadeyesDocument4 pagesContoh Perhitungan Lifting Set Dan Padeyesnur azisPas encore d'évaluation
- 3 Re 445 DSL SPC PDFDocument58 pages3 Re 445 DSL SPC PDFThomasBaby KavoorazhikathuPas encore d'évaluation
- 2013 SKF Training Handbook: Reliability Maintenance InstituteDocument134 pages2013 SKF Training Handbook: Reliability Maintenance InstituteBalázs HernádiPas encore d'évaluation
- AI Based Design of A FLC Scheme For 2Document19 pagesAI Based Design of A FLC Scheme For 2Kafar KhanPas encore d'évaluation
- Applying Appropriate SealantDocument64 pagesApplying Appropriate SealantShina AbieraPas encore d'évaluation
- Invacare Homefill Compressor ManualDocument36 pagesInvacare Homefill Compressor ManualhmiklitzPas encore d'évaluation