INTRODUCCIN Con frecuencia se tienen que estimar valores intermedios entre valores conocidos.

El mtodo ms comn empleado para este propsito es la interpolacin polinomial. Recurdese que la frmula general de un polinomio de n-simo orden es: (1)

Para n + 1 puntos, existe uno y slo un polinomio de n-simo orden o menor que pasa a travs de todos los puntos. Por ejemplo, hay slo una lnea recta (es decir un polinomio de primer orden) que conecta dos puntos. El polinomio de interpolacin consiste en determinar el nico polinomio de n-simo orden que se ajusta a los n + 1 puntos dados. Este polinomio proporciona una frmula para calcular los valores intermedios. Aunque existe uno y slo un polinomio de n-simo orden que se ajusta a los n + 1 puntos, existen una gran variedad de frmulas matemticas mediante las cuales se puede expresar este polinomio. En esta unidad se estudian dos tcnicas alternativas que estn bien condicionadas para implementarse en una computadora. Estos son los polinomios de Newton y de Lagrange. POLINOMIOS DE INTERPOLACIN CON DIFERENCIAS DIVIDIDAS DE NEWTON INTERPOLACIN LINEAL La frmula ms simple de interpolacin es la de conectar dos puntos con una lnea recta. Este mtodo, llamado Interpolacin Lineal, se muestra en la figura 1.

Fig. 1

Usando tringulos semejantes, se tiene:

(2)

Que se puede reordenar como:

(3)

La cul es la frmula de interpolacin lineal. La notacin f1(X) indica que se trata de un polinomio de interpolacin de primer orden. Ntese que adems de representar la pendiente de la lnea que conecta los dos puntos, el trmino [f(X1) - f(X2)] / (X1 - X2) es una aproximacin de diferencias divididas finitas a la primera derivada. En general, entre ms pequeo sea el intervalo entre los puntos, ms exacta ser la aproximacin. EJEMPLO Calclese el logaritmo natural de 2 (ln 2) usando interpolacin lineal. Primero, llvese a cabo los clculos interpolando entre ln 1 = 0 y ln 6 = 1.7917595. Despus reptase el procedimiento, pero usando un intervalo ms pequeo desde ln 1 a ln 4 = 1.3862944. Ntese que el valor real de ln 2 = 0. 69314718 SOLUCIN: Evaluando la frmula de interpolacin lineal (3) de X = 1 a X = 6 da:

La cual representa un error porcentual de e% = 48.3 %. Usando el intervalo ms pequeo desde X = 1 a X = 4 da:

Por lo contrario, usando el intervalo ms pequeo reduce el error relativo porcentual a e% = 33.3%. INTERPOLACIN CUADRTICA El error en el ejemplo anterior se debe a que se aproxima a una curva mediante una lnea recta. Por consiguiente, una estrategia que mejora la aproximacin es la de introducir cierta curvatura en a lnea que conecta a los puntos. Si se dispone de tres puntos lo anterior se puede llevar a cabo con un polinomio de segundo orden (llamado tambin polinomio cuadrtico o parbola). Una manera conveniente para este caso es: (4) Ntese que aunque la ecuacin (4) parezca diferente de la ecuacin general de un polinomio (1), las dos ecuaciones son equivalentes.

Esto se puede demostrar si se multiplican los trminos de la ecuacin (4) y obtener: (5) o, agrupar trminos: (6) en donde:

(7)

De esta manera, las ecuaciones (1) y (4) son frmulas alternativas equivalentes del nico polinomio de segundo grado que une a los tres puntos. Se puede usar un procedimiento simple para determinar los valores de los coeficientes. Para b0, se usa la ecuacin (4) con X = X0, y se obtiene b0 = f(X0) (8) sustituyendo la ecuacin (8) en la ecuacin (4) y evaluando en X = X1 se obtiene:

(9)

Y por ltimo, las ecuaciones (8) y (9) se sustituyen en la ecuacin (4), y se evalua sta en X = X2 y se obtiene:

(10)

Ntese que, al igual que en el caso de interpolacin lineal, b1 an representa la pendiente de la lnea que une los puntos X0 y X1. Por lo tanto, los primeros dos trminos de la ecuacin (4) son equivalentes a la interpolacin de X0 a X1, como se especific anteriormente en la ecuacin (3). El ltimo trmino, b2(X-X0)(X-X1), introduce la curvatura de segundo orden en la frmula. Ejemplo Ajstese el polinomio de segundo orden a los tres puntos usados en el ejemplo anterior X0 = 1 f (X0) = 0.0000 000 X1 = 4 f (X1) = 1.3862 944 X2 = 6 f (X2) = 1.7917 595 3

sese el polinomio para evaluar ln 2 SOLUCIN: Aplicando la ecuacin (8) da: b0 = 0 la ecuacin (9) genera:

Y la ecuacin (10) da:

Sustituyendo estos valores en la ecuacin (4) se obtiene la frmula cuadrtica: f2 ( X ) = 0 + 0.4620981 (X - 1) - 0.05187312 (X - 1) (X - 4) que se evalua en X = 2 y se obtiene f2 ( 2 ) = 0.5658443 Lo que representa un error porcentual del e% = 18.4%. Por lo tanto, mejora la interpolacin comparada con los resultados obtenidos al usar una lnea recta (del ejemplo anterior). INTERPOLACIN POLINOMIAL DE LAS DIFERENCIAS FINITAS DE NEWTON El anlisis anterior se puede generalizar en el ajuste de un polinomio de n-simo orden a los n+1 puntos. El polinomio de n-simo orden es: (11) Como se hizo anteriormente con las interpolaciones lineales y cuadrticas, se usan los puntos en la evaluacin de los coeficientes b0, b1, ... , bn. Se requieren n + 1 puntos para obtener un polinomio de n-simo orden: X0, X1, ... , Xn. Usando estos datos, con las ecuaciones siguientes se evalan los coeficientes: b0 = f (X0) b1 = f [X1, X0] b2 = f [X2, X1, X0] (12) ... bn = f [X n, Xn-1, ..., X1, X0] 4

En donde las evaluaciones de la funcin entre corchetes son diferencias divididas finitas. Por ejemplo, la primera diferencia dividida finita se representa generalmente como:

(13)

La segunda diferencia dividida finita, que representa la diferencia de dos primeras diferencias divididas finitas, se expresa generalmente como: (14) De manera similar, la n-sima diferencia dividida finita es:

(15)

Estas diferencias se usan para evaluar los coeficientes de la ecuacin (12), los cuales se sustituyen en la ecuacin (11), para obtener el polinomio de interpolacin: f n (X) = f(X0) + (X-X0) f[X1, X0] + (X-X0)(X-X1) f[X2, X1, X0] + (16) ...+ (X-X0)(X-X1)...(X-Xn-1) f[Xn, Xn-1,...,X1, X0] Al cual se le llama Polinomio de Interpolacin con Diferencias Divididas de Newton. Se debe notar que no es necesario que los datos usados en la ecuacin (16) estn igualmente espaciados o que los valores de la abscisa necesariamente se encuentren en orden ascendente, como se ilustra en el ejemplo 3.3 Todas las diferencias pueden arreglarse en una tabla de diferencias divididas, en donde cada diferencia se indica entre los elementos que la producen:

i 0 1 2 3

Xi X0 X1 X2 X3

f(Xi) f(X0) f(X1) f(X2) f(X3)

Primera f(X1, X0) f(X2, X1) f(X3,X2)

Segunda f(X2, X1, X0) f(X3, X2, X1)

Tercera f(X3, X2, X1, X0)

EJEMPLO Usando la siguiente tabla de datos, calclese ln 2 con un polinomio de interpolacin de Newton con diferencias divididas de tercer orden: X 1 4 6 5 SOLUCIN: El polinomio de tercer orden con n = 3, es. f(X) 0.000 0000 1.386 2944 1.791 7595 1.609 4379

Las primeras diferencias divididas del problema son:

Las segundas diferencias divididas son:

La tercera diferencia dividia es:

Los resultados para f(X1, X0), f(X2, X1, X0) y f(X3, X2, X1, X0) representan los coeficientes b1, b2 y b3 Junto con b0 = f (X0) = 0.0, la ecuacin da: f3 (X) = 0 + 0.46209813 (X-1) - 0.0518731 (X-1)(X-4) + 0.0078655415 (X-1)(X-4)(X-6) 6

Arreglando la tabla de diferencias X f [X] f1[] f2[] f3[]

1.0 0.00000000 0.46209813 - 0.051873116 0.0078655415 4.0 1.3862944 6.0 1.7917595 5.0 1.6094379 0.20273255 - 0.020410950 0.18232160

Con la ecuacin anterior se puede evaluar para X = 2 f3 (2) = 0.62876869 lo que representa un error relativo porcentual del e% = 9.3%. Ntese que la estructura de la ecuacin (16) es similar a la expresin de la serie de Taylor en el sentido de que los trminos agregados secuencialmente consideran el comportamiento de orden superior de la funcin representada. Estos trminos son diferencias divididas finitas, y por lo tanto, representan aproximaciones a las derivadas de orden superior. En consecuencia, como sucede con la serie de Taylor, si la funcin representativa es un polinomio de nsimo orden, el polinomio interpolante de n-simo orden bajado en n + 1 llevar a resultados exactos. El error por truncamiento de la serie de Taylor es: (17)

En donde es un punto cualquiera dentro del intervalo (Xi, Xi+1). Una relacin anloga del error en un polinomio interpolante de n-simo orden est dado por: (18) En donde es un punto cualquiera dentro del intervalo que contiene las incgnitas y los datos. Para uso de esta frmula la funcin en cuestin debe ser conocida y diferenciable. Y usualmente, este no es el caso. Afortunadamente existe una frmula alternativa que no requiere conocimiento previo de la funcin. En vez de ello, se usa una diferencia dividida finita que aproxima la (n+1)-sima derivada: Rn = f [X, Xn, Xn-1, ... , X1, X0](X-X0)(X-X1)...(X-Xn) (19) en donde f(X, Xn, Xn-1, ... , X0) es la (n+1)-sima diferencia dividida. Ya que la ecuacin (19) contiene la incgnita f(X), sta no se puede resolver y obtener el error. Sin embargo, si se dispone de un dato adicional f (Xn+1), la ecuacin (19) da una aproximacin del error como: (20) 7

 POLINOMIOS DE INTERPOLACIN DE LAGRANGE El polinomio de interpolacin de Lagrange, simplemente es una reformulacin del polinomio de Newton que evita los clculos de las diferencias divididas. Este se puede representar concretamente como:

(21)

en donde:

(22)

En donde

denota el "producto de".

Por ejemplo, la versin lineal (n = 1) es:

(23)

y la versin de segundo orden es: (24)

al igual que en el mtodo de Newton, la versin de Lagrange tiene un error aproximado dado por: (25)

La ecuacin (21) se deriva directamente del polinomio de Newton. Sin embargo, la razn fundamental de la formulacin de Lagrange se puede comprender directamente notando que cada trmino Li(X) ser 1 en X=Xi y 0 en todos los dems puntos. Por lo tanto, cada producto Li(X) f(Xi) toma un valor de f(Xi) en el punto Xi. Por consiguiente la sumatoria de todos los productos, dada por la ecuacin (21) es el nico polinomio de n-simo orden que pasa exactamente por los n+1 puntos.

Ejemplo sese un polinomio de interpolacin de Lagrange de primer y segundo orden para evaluar ln 2 en base a los datos: i 0 1 2 X 1.0 4.0 6.0 f(X) 0.000 0000 1.386 2944 1.791 7595

Solucin: El polinomio de primer orden es:

y, por lo tanto, la aproximacin en X = 2 es

de manera similar, el polinomio de segundo orden se desarrolla como:

Como se expresaba, ambos resultados son similares a los que se obtuvieron previamente usando la interpolacin polinomial de Newton. En resumen, para los casos en donde el orden del polinomio se desconozca, el mtodo de Newton tiene ventajas debido a que profundiza en el comportamiento de las diferentes frmulas de orden superior. Adems la aproximacin del error dada por la ecuacin (20), en general puede integrarse fcilmente en los clculos de Newton ya que la aproximacin usa una diferencia dividida. De esta forma, desde el punto de vista de clculo, a menudo, se prefiere el mtodo de Newton. Cuando se va a llevar a cabo slo una interpolacin, ambos mtodos, el de Newton y el de Lagrange requieren de un esfuerzo de clculo similar. Sin embargo, la versin de Lagrange es un poco ms fcil de programar. Tambin existen casos en donde la forma de Newton es ms susceptible a los errores de redondeo. Debido a esto y a que no se requiere calcular y almacenar diferencias divididas, la forma de Lagrange se usa, a menudo, cuando el orden del polinomio se conoce a priori.

 DIFERENCIACIN NUMRICA

INTRODUCCIN Concentremos ahora nuestra atencin a procedimientos para diferenciar numricamente funciones que estn definidas mediante datos tabulados o mediante curvas determinadas en forma experimental. Un mtodo consiste en aproximar la funcin en la vecindad del punto en que se desea la derivada, mediante una parbola de segundo, tercer o mayor grado, y utilizar entonces la derivada de la parbola en ese punto como la derivada aproximada de la funcin. Otro ejemplo, que comentaremos aqu, utiliza los desarrollos en serie de Taylor. La serie de Taylor para una funcin Y = f(X) en , desarrollada con respecto al punto Xi es (1)

En donde Yi es la ordenada que corresponde a Xi y para est dada en forma similar por:

se encuentra en la regin de convergencia. La funcin

(2)

Utilizando solamente los tres primeros trminos de cada desarrollo, podremos obtener una expresin para Y'i restando la ec. (2) de la ec. (1), (3)

DIFERENCIAS CENTRALES, HACIA ADELANTE Y HACIA ATRS

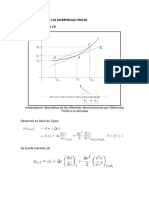
Fig. 1

10

Observando la figura (1), vemos que si designamos los puntos uniformemente espaciados a la derecha de Xi como Xi+1 , Xi+2, etc. y los puntos a la izquierda de Xi como Xi-1, Xi-2 , etc. e identificamos las ordenadas correspondientes como Yi+1, Yi+2, Yi-1, Yi-2, respectivamente, la ec. (3) se puede escribir en la forma: (4)

La ec. (4) se denomina la primera aproximacin, por Diferencias Centrales de Y', para X. La aproximacin representa grficamente la pendiente de la recta discontinua mostrada en la figura 1. La derivada real se representa mediante la lnea slida dibujada como tangente a la curva en Xi. Si sumamos las ecuaciones (1) y (2) y utilizamos la notacin descrita previamente, podemos escribir la siguiente expresin para la segunda derivada: (5)

La ec. (5) es la primera aproximacin, por Diferencias Centrales, de la segunda derivada de la funcin en Xi. Esta expresin se puede interpretar grficamente como la pendiente de la tangente a la curva en Xi+1/2 menos la pendiente de la tangente a la curva en Xi-1/2 dividida entre , cuando las pendientes de las tangentes estn aproximadas mediante las expresiones:

(6)

es decir, (7)

Para obtener una expresin correspondiente a la tercera derivada, utilizamos cuatro trminos en el segundo miembro de cada una de las ecs. (1) y (2). Restando la ec. (2) de la ec. (1) se obtiene: (8) Si desarrollamos la serie de Taylor respecto a Xi para obtener expresiones correspondientes a Y = f(X) en y , respectivamente, obtenemos:

(9) 11

Restando la primera ec. (9) de la segunda, y utilizando solamente los cuatro trminos mostrados para cada desarrollo, se obtiene: (10)

La solucin simultnea de las ecs. (8) y (10) produce la tercera derivada: (11)

La ec. (11) es la primera expresin de Diferencias Centrales correspondiente a la tercera derivada de Y en Xi. Por este mtodo se pueden obtener derivadas sucesivas de mayor orden, pero como requieren la solucin de un nmero cada vez mayor de ecuaciones simultneas, el proceso se vuelve tedioso. La misma tcnica se puede utilizar tambin para encontrar expresiones ms precisas de las derivadas utilizando trminos adicionales en el desarrollo en serie de Taylor. Sin embargo, la derivacin de expresiones ms precisas, especialmente para derivadas de orden superior al segundo, se vuelve muy laboriosa debido al nmero de ecuaciones simultneas que se deben resolver. No se presentan aqu esas derivaciones, pero dichas expresiones, para diferentes derivadas, se incluyen en el resumen que sigue a estos comentarios. Las expresiones correspondientes a las derivadas de mayor orden se logran con mucha mayor facilidad y bastante menos trabajo, utilizando operadores de diferencias, de promedios y de derivacin. Este mtodo se encuentra fuera de los alcances fijados, pero se pueden encontrar en varios libros referentes al anlisis numrico. Se ha demostrado que las expresiones de Diferencias Centrales para las diversas derivadas encierran valores de la funcin en ambos lados del valor X en que se desea conocer la derivada en cuestin. Utilizando desarrollos convenientes en serie de Taylor, se pueden obtener fcilmente expresiones para las derivadas, completamente en trminos de valores de la funcin en Xi y puntos a la derecha de Xi. Estas se conocen como expresiones de Diferencias Finitas Hacia Adelante. En forma similar, se pueden obtener expresiones para las derivadas que estn totalmente en trminos de valores de la funcin en Xi y puntos a la izquierda de Xi. Estas se conocen como expresiones de Diferencias Finitas Hacia Atrs. En la diferenciacin numrica, las expresiones de diferencias hacia adelante se utilizan cuando no se dispone de datos a la izquierda del punto en que se desea calcular la derivada, y las expresiones de diferencias hacia atrs, se utilizan cuando no se dispone de datos a la derecha del punto deseado. Sin embargo, las expresiones de diferencias centrales son ms precisas que cualquiera de las otras dos. RESUMEN DE FRMULAS DE DIFERENCIACIN Lo que sigue es un resumen de las frmulas de diferenciacin que se pueden obtener a base de desarrollos en serie de Taylor.

12

 Expresiones de Primeras Diferencias Centrales

(12)

Expresiones de Segundas Diferencias Centrales

(13)

Expresiones de Primeras Diferencias Hacia Adelante

(14)

Expresiones de Segundas Diferencias Hacia Adelante

(15)

Expresiones de Primeras Diferencias Hacia Atrs

(16) 13

 Expresiones de Segundas Diferencias Hacia Atrs

(17)

EJEMPLO sense aproximaciones de Diferencias Finitas Hacia Adelante, Hacia Atrs y Centradas para estimar la primera derivada de:

utilizando un tamao de paso de Repetir los clculos usando

= 0.5.

= 0.25.

Ntese que la derivada se puede calcular directamente como:

y evaluando tenemos: F'(0.5) = -0.9125 SOLUCIN: Para = 0.5 se puede usar la funcin para determinar: Xi-1 = 0.0 Xi = 0.5 Xi+1 = 1.0 Yi-1 = 1.200 Yi = 0.925 Yi+1 = 0.200

Estos datos se pueden utilizar para calcular la Diferencia Hacia Adelante:

la Diferencia Dividida Hacia Atrs ser: 14

y la Diferencia Dividida Central:

Para

= 0.25, los datos son: Xi-1 = 0.25 Xi = 0.50 Xi+1 = 0.75 Yi-1 = 1.10351563 Yi = 0.92500000 Yi+1 = 0.63632813

que se usarn para calcular la Diferencia Dividida Hacia Adelante:

la Diferencia Dividida Hacia Atrs:

y la Diferencia Dividida Central:

INTEGRACIN NUMRICA INTRODUCCIN En ingeniera se presenta con frecuencia la necesidad de integrar una funcin que sera, en general, de una de las tres formas siguientes: 1. Una funcin simple y continua tal como un polinomio, una funcin exponencial o una funcin trigonomtrica. 2. Una funcin complicada y continua que es difcil o imposible de integrar directamente. 3. Una funcin tabulada en donde los valores de X y f(X) se dan en un conjunto de puntos discretos, como es el caso a menudo, de datos experimentales. 15

En el primer caso, la integral simplemente es una funcin que se puede evaluar fcilmente usando mtodos analticos aprendidos en el clculo. En los dos ltimos casos, sin embargo, se deben emplear mtodos aproximados. Las frmulas de integracin de Newton-Cotes son los esquemas ms comunes dentro de la integracin numrica. Se basan en la estrategia de reemplazar una funcin complicada o un conjunto de datos tabulares con alguna funcin aproximada que sea ms fcil de integrar. La integral se puede aproximar usando una serie de polinomios aplicados por partes a la funcin o a los datos sobre intervalos de longitud constante. Se dispone de las formas abierta y cerrada de las frmulas de Newton-Cotes. Las formas cerradas son aquellas en donde los puntos al principio y al final de los lmites de integracin se conocen. Las frmulas abiertas tienen los lmites de integracin extendidos ms all del rango de los datos. Las frmulas abiertas de Newton-Cotes, en general, no se usan en la integracin definida. Sin embargo, se usan extensamente en la solucin de ecuaciones diferenciales ordinarias. REGLA DEL TRAPECIO La regla del trapecio o regla trapezoidal es una de las frmulas cerradas de Newton-Cotes. Considrese la funcin f(X), cuya grfica entre los extremos X = a y X = b se muestra en la fig. 1. Una aproximacin suficiente al rea bajo la curva se obtiene dividindola en n fajas de ancho mediante un trapecio, como se indica en la figura. y aproximando el rea de cada faja

Fig. 1

Llamando a las ordenadas Y i (i = 1, 2, 3, ...., n+1), las reas de los trapecios son:

(1)

16

El rea total comprendida entre X = a y X = b est dada por:

(2)

Sustituyendo las ecs. (1) en esta expresin se obtiene:

(3)

La cual recibe el nombre de Frmula Trapezoidal, y se puede expresar como:

(4)

En esencia, la tcnica consiste en dividir el intervalo total en intervalos pequeos y aproximar la curva Y = f(X) en los diversos intervalos pequeos mediante alguna curva ms simple cuya integral puede calcularse utilizando solamente las ordenadas de los puntos extremos de los intervalos. Si la funcin f(X) se puede expresar como una funcin matemtica continua que tiene derivadas continuas f'(X) y f''(X), el error que resulta de aproximar el rea verdadera en una faja bajo la curva f(X) comprendida entre Xi y Xi+1 mediante el rea de un trapecio, se demuestra que es igual a: (5)

Este error es la cantidad que se debe agregar al rea del trapecio para obtener el rea real. Se llama Error por Truncamiento, ya que es el error que resulta de utilizar una serie de Taylor truncada, en vez de una serie de Taylor completa, para representar en forma de serie el rea de una faja. Generalmente no se puede valuar directamente el trmino mostrado como error por truncamiento. Sin embargo, se puede obtener una buena aproximacin de su valor para cada faja suponiendo que f '' es suficientemente constante en el intervalo de la faja (se supone que las derivadas de orden superior son despreciables) y evaluando f '' para . La estimacin del error por truncamiento para la integracin total se obtiene sumando las estimaciones para cada faja. Si la estimacin obtenida para el error total por truncamiento es mayor de lo que se puede tolerar, se debe utilizar una faja ms angosta o un mtodo ms preciso. Otro error que se introduce al obtener el rea aproximada de cada faja es el Error por Redondeo. Este se produce cuando las operaciones aritmticas requeridas se efectan con valores numricos que tienen un nmero limitado de dgitos significativos. Se puede demostrar que una aproximacin al lmite del error por redondeo es:

(6) 17

Tenemos entonces que el lmite en el error por redondeo aumenta proporcionalmente a , lo cual pronto domina al error por truncamiento que es proporcional a . En realidad, el error por redondeo en s no crece proporcionalmente con sino con truncamiento si decrece lo suficiente. en que 0 < p < 1, pero sin embargo an supera al error por

El error por redondeo se puede minimizar utilizando aritmtica de doble precisin o mediante compiladores que pueden manejar un gran nmero de dgitos significativos. De la informacin anterior se puede ver que el error total en el intervalo de integracin deseado, es la suma de los errores de truncamiento y redondeo. Si el error total se debiera nicamente al error por truncamiento, se podra hacer tan pequeo como se deseara reduciendo suficientemente el ancho de la faja. Por ejemplo, bisecando el ancho de la faja se duplicara el nmero de errores por truncamiento que hay que sumar, pero la expresin para el error en cada faja indica que cada uno sera aproximadamente un octavo de su valor previo. Sin embargo, disminuyendo el ancho de la faja se afectara tambin el error total al aumentar el error por redondeo, debido al mayor nmero de operaciones que hay que efectuar al valuar la ec. (3). Entonces, cuando se disminuye el ancho de la faja para disminuir el error total, existe un punto ptimo en el cual disminuciones adicionales del ancho de la faja haran que el error aumentara en lugar de disminuir, porque el error por redondeo se volvera dominante. El ancho ptimo de la faja para una funcin especial se puede determinar fcilmente en forma experimental en la computadora (suponiendo que el rea real bajo la grfica de la funcin se puede valuar) pero es difcil definirlo analticamente. REGLA DE SIMPSON Adems de aplicar la regla trapezoidal con segmentos cada vez ms finos, otra manera de obtener una estimacin ms exacta de una integral, es la de usar polinomios de orden superior para conectar los puntos. Por ejemplo, si hay un punto medio extra entre f(a) y f(b), entonces los tres puntos se pueden conectar con un polinomio de tercer orden. A las frmulas resultantes de calcular la integral bajo estos polinomios se les llaman Reglas de Simpson. REGLA DE SIMPSON 1/3 La Regla de Simpson de 1/3 proporciona una aproximacin ms precisa, ya que consiste en conectar grupos sucesivos de tres puntos sobre la curva mediante parbolas de segundo grado, y sumar las reas bajo las parbolas para obtener el rea aproximada bajo la curva. Por ejemplo, el rea contenida en dos fajas, bajo la curva f(X) en la fig. 2, se aproxima mediante el rea sombreada bajo una parbola que pasa por los tres puntos: (Xi , Yi), (Xi+1, Yi+1), (X i+2, Y i+2)

Fig. 2

18

Por conveniencia al derivar una expresin para esta rea, supongamos que las dos fajas que comprenden el rea bajo la parbola se encuentran en lados opuestos del origen, como se muestra en la fig. 3. Este arreglo no afecta la generalidad de la derivacin. La forma general de la ecuacin de la parbola de segundo grado que conecta los tres puntos es: (7)

La integracin de la ec. (7) desde parbola. Por lo tanto:

hasta

proporciona el rea contenida en las dos fajas mostradas bajo la

(8)

Fig. 3

La sustitucin de los lmites en la ec. (8) produce: (9)

Las constantes a y c se pueden determinar sabiendo que los puntos , (0, Yi + 1 ), y satisfacer la ec. (7). La sustitucin de estos tres pares de coordenadas en la ec. (7) produce:

deben

(10)

La solucin simultnea de estas ecuaciones para determinar las constantes a, b, c, nos lleva a: 19

(11)

La sustitucin de la primera y tercera partes de la ec. (11) en la ec. (9) produce:

(12)

que nos da el rea en funcin de tres ordenadas Yi, Y i+1, Y i+2 y el ancho

de una faja.

Esto constituye la regla de Simpson para determinar el rea aproximada bajo una curva contenida en dos fajas de igual ancho. Si el rea bajo una curva entre dos valores de X se divide en n fajas uniformes (n par), la aplicacin de la ec. (12) muestra que:

(13)

Sumando estas reas, podemos escribir:

o bien

(14)

(15)

en donde n es par. La ec. (15) se llama Regla de Simpson de un Tercio para determinar el rea aproximada bajo una curva. Se puede utilizar cuando el rea se divide en un nmero par de fajas de ancho .

20

Si la funcin f(X) se puede expresar como una funcin matemtica continua que tiene derivadas continas f ' ha , el error que resulta de aproximar el rea verdadera de dos fajas bajo la curva f(X) comprendida entre X i-1 y X i+1 mediante el rea bajo una parbola de segundo grado, se demuestra que es:

(16)

Este error por truncamiento es la cantidad que se debe agregar al rea aproximada de dos fajas, que se obtiene mediante la regla de un tercio de Simpson, para obtener el rea real bajo la curva en ese intervalo. El trmino mostrado del error por truncamiento generalmente no se puede valuar en forma directa. Sin embargo, se puede obtener una buena estimacin de su valor para cada intervalo de dos fajas suponiendo que es suficientemente para

constante en el intervalo (se supone que las derivadas de orden superior son despreciables) y valuando

. La estimacin del error por truncamiento para toda la integracin se obtiene sumando las estimaciones correspondientes a cada dos fajas. Si la estimacin del error total por truncamiento es mayor de lo que se puede tolerar, se deben utilizar intervalos de dos fajas menores. Considerando el error por redondeo que tambin aparece, existe un ancho ptimo de la faja para obtener un error total mnimo en la integracin. REGLA DE SIMPSON 3/8 La derivacin de la Regla de los Tres Octavos de Simpson es similar a la regla de un tercio, excepto que se determina el rea bajo una parbola de tercer grado que conecta 4 puntos sobre una curva dada. La forma general de la parbola de tercer grado es: (17)

Fig. 4

En la derivacin, las constantes se determinan requiriendo que la parbola pase a travs de los cuatro puntos indicados sobre la curva mostrada en la fig. 4. El intervalo de integracin es de que produce: a , lo

21

(18)

que es la regla de los tres octavos de Simpson. La regla de Simpson de 3/8 tiene un error por truncamiento de: (19)

Por lo tanto es algo ms exacta que la regla de 1/3. La regla de Simpson de 1/3 es, en general, el mtodo de preferencia ya que alcanza exactitud de tercer orden con tres puntos en vez de los cuatro puntos necesarios para la versin de 3/8. No obstante la regla de 3/8 tiene utilidad en las aplicaciones de segmentos mltiples cuando el nmero de fajas es impar. EJEMPLO 1. Utilcese la regla trapezoidal de cuatro segmentos o fajas para calcular la integral de

Desde a = 0 hasta b = 0.8 y calcular el error sabiendo que el valor correcto de la integral es 1.64053334. SOLUCIN n=4

X 0.0 0.2 0.4 0.6 0.8

f(X) 0.200 1.288 2.456 3.464 0.232 22

usando la frmula trapezoidal:

Ex = 1.64053334 - 1.4848 = 0.15573334 e% = 9.5 % 2. Utilcese la regla de Simpson de 1/3 con n = 4 para calcular la integral del inciso anterior SOLUCIN n=4

X 0.0 0.2 0.4 0.6 0.8

f(X) 0.200 1.288 2.456 3.464 0.232

usando la regla de Simpson de 1/3

Ex = 1.64053334 - 1.62346667 = 0.01706667 e% = 1.04 % 3. Utilcese la regla de Simpson de 3/8 para calcular la integral anterior: SOLUCIN Como se requieren cuatro puntos o tres fajas para la regla de Simpson de 3/8, entonces:

23

X 0.0000 0.2667 0.5333 0.8000

f(X) 0.20000000 1.43286366 3.48706521 0.23200000

usando la ecuacin de Simpson de 3/8

Ex = 1.64053334 - 1.51917037 = 0.121164 e% = 7.4 % 4. Utilcese en conjuncin las reglas de Simpson de 1/3 y 3/8 para integrar la misma funcin usando cinco segmentos. SOLUCIN Los datos necesarios para la aplicacin de cinco segmentos (h = 0.16) son: X 0.00 0.16 0.32 0.48 0.64 0.80 f(X) 0.20000000 1.29691904 1.74339328 3.18601472 3.18192896 0.23200000

La integral de los primeros dos segmentos se obtiene usando la regla de Simpson de 1/3:

24

Para los ltimos tres segmentos, se usa la regla de Simpson de 3/8 para obtener:

La integral total se calcula sumando los dos resultados: I = 0.38032370 + 1.26475346 = 1.64507716 ex = 1.64053334 - 1.64507716 = -0.00454383 e% = -0.28 %

25

 BIBLIOGRAFA http://luda.azc.uam.mx/curso2/cp2indic.html Akai Terrence J., Mtodos numricos aplicados a la ingeniera. Mxico, Limusa Wiley, 2004. Burden Richard L. & Faires J. Douglas, Anlisis numrico. 2. ed., Mxico, Grupo Editorial Iberoamrica, 1993. Chapra Steven C. & Canale Raymond P., Mtodos numricos para ingenieros. 4. ed., Mxico, McGraw-Hill, 2003. Iriarte R. & Balderrama V., Mtodos numricos. Mxico, Facultad de Ingeniera U.N.A.M., Trillas, 1990.

26