1 09-04-2008

e
st
, s C are eigenfunctions of a SISO LT I system.
SYS u(t) y(t)
e
st
e
st
Figure 1: Eigenfunction input-output on a linear system.
(s) =
q(s)
r(s)
where,
q(s) =
m
s
m
+ . . . +
1
s +
0
r(s) = s
n
+
n1
s
n1
+ . . . +
1
s +
0
even if, u(t) 0
t
we can have output solutions y(t) = Ce
pt
:
Cr(p)e
pt
= 0
t0
for any p such that r(p) = 0.
Consequently: p is a zero of polynomial r; where r has n such zeros p
k
,
for k = 1, . . . , n.
r(s) = (s p
1
)(s p
2
)(s p
n
)
=
n

k=1
(s p
k
)
e
p
k
t
for any p
k
which is a zero of polynomial r(s) are component solutions
which can occur even with no inputs acting on the system.
e
p
k
t
motions are intrinsic to the system dynamics; therefore, we some-
times call them the natural modes of the system.
*Note that any combination of modes is a valid zero-input solution as well.
n

k=1
c
k
r(p
k
)e
p
k
t
= 0
1
c
k
C k = 1, . . . , n
p
k
[zeros of r(s)] k = 1, . . . , n
Any combination of modes is a valid zero-input solution. Typically called
the homogenous, unforced, or free response.
y
h
= homogenous solution
more generally, when u(t) = e
st
we have solutions of the form:
y(t) = (s)e
st
. .
particularorforcedy
p
(t)
+
n

k=1
c
k
e
p
k
t
. .
y
h
(t)
Some properties of homogenous solutions. . .
Stability
|y
h
(t)| 0 as t
Then:
y(t) y
p
(t)
|e
p
k
t
| 0 as t for all k = 1, . . . , n
p
k
=
k
+ j
k

k
,
k
R
e
p
k
t
= e

k
t
e
j
k
t
|e
p
k
t
| = |e

k
t
|
| | = 1
..
|e
j
k
t
| = |e

k
t
|
stability of mode e
p
k
t
is determined by
k
= Re{p
k
}
lim
t
|e
p
k
t
| = lim
t
|e

k
t
|
therefore; the mode is stable if Re{p
k
} < 0 and the system is stable if
Re{p
k
} < 0 for all k = 1, . . . , n.
Stable modes for LT I systems decay exponentially fast, faster the more neg-
ative is
k
.
2
Unstable
RHP
Re
Im
Faster
convergence to Zero
X
Stable
LHP

k
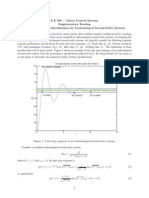
Figure 2: Stability diagram and decay rate due to .
Re
Im

max

min

min
0
1
Lines of constant
damping ratio
Figure 3: Typical design (synthesis) constraint. Ensure Re{p
k
} <
max
for
all k = 1, . . . , n.
more generally:
e
p
k
t
= e
t
[cos
k
t + j sin
k
t]
if
k
= Im{p
k
} = 0 the mode will exhibit oscillations. Assuming the mode
is stable then the damping ratio is dened as:

k
=
|Re{p
k
}|
|p
k
|
=
|
k
|
_

2
k
+
2
k
3
for
k

= 0 mode will exhibit very pronounced oscillations
for
k

= 1 mode will exhibit negligibly observable oscillations
Typical design (synthesis) constraint ensures

k
>
min
for k = 1, . . . , n
Examination of forced component solutions
u(t) = e
st
y
p
(t) = (s)e
st
Q: can we get y
p
(t) = 0?
A: Yes if (s) = 0
(s) =
q(s)
r(s)
= 0
_
r(s) = not possible for ninite values of s
q(s) = 0
In general, q(s) = 0 has m solutions, z
i
for i = 1, . . . , m
q(s) =
m
(s z
1
)(s z
2
) . . . (s z
m
)
=
m
m

i=1
(s z
i
)
Thus:
u(t) = e
z
i
t
where z
i
is any zero of q(s) (in the steady state).
y
p
(t) = 0
Now suppose u(t) = e
st
Re{s} = 0 s = j
u(t) = e
jt
= cos t + j sin t
y
p
(t) = (j)e
jt
= M()[cos (t + ()) + j sin (t + ())]
4
where,
M() = |(j)|
() = (j)
if
u
1
(t) = Im{e
jt
} = sin t
then
y
p
1
(t) = Im{(j)e
jt
}
= M() sin (t + ())
or similarly
u
2
(t) = Re{e
jt
} = cos t
then
y
p
2
(t) = Re{(j)e
jt
}
= M() cos (t + ())
SYS
sin[t] M()sin[t+()]
Figure 4: Sinusoidal input to a linear system.
M() = |(j)|
() = (j)
We can plot amplitude M() and phase () as a function of driving fre-
quency: [0, ). This leads to the use of Bode diagrams.
Finally look at arbitrary inputs:
u(t) =
n

k=1
U
k
e
s
k
t
y
p
(t) =
n

k=1
Y
k
e
s
k
t
5
where, U
k
C, s
k
C Y
k
=
k
(s
k
)U
k
Again, by direct subsitution into the dierential equation:
y
p
(t) =
n

k=1
(s
k
)U
k
e
s
k
t
arguments hold for n . This also holds in the dierential limit, i.e.
u(t) =
_
U(s)e
st
ds
y
p
(t) =
_
Y (s)e
st
ds
Y (s) = (s)U(s) foralls C
6