Académique Documents
Professionnel Documents
Culture Documents
Textbook Distribution-Tables
Transféré par
kakkrasDescription originale:
Titre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Textbook Distribution-Tables
Transféré par
kakkrasDroits d'auteur :
Formats disponibles
Compare Distribution Tables
Page 1 of 1
Creators of STATISTICA Data Analysis Software and Services
StatSoft.com Textbook Distribution Tables
Elementary Concepts Statistics Glossary
Compare Distribution Tables
Compared to probability calculators (e.g., the one included in STATISTICA), the traditional format of distribution tables such as those the advantage of showing many values simultaneously and, thus, enables the user to examine and quickly explore ranges of
Basic Statistics ANOVA / MANOVA Association Rules Boosting Trees Canonical Analysis CHAID Analysis C & R Trees Classification Trees Cluster Analysis Correspondence Analysis Data Mining Techniques Discriminant Analysis Distribution Fitting Experimental Design Factor Analysis General Discrim. Analysis General Linear Models Generalized Additive Mod. Generalized Linear Mod. General Regression Mod. Graphical Techniques Ind.Components Analysis Linear Regression Log-Linear Analysis MARSplines Machine Learning Multidimensional Scaling Neural Networks Nonlinear Estimation
alpha=.10 alpha=.025 alpha=.05 alpha=.01 Note that all table values were calculated using the distribution facilities in STATISTICA BASIC, and they were verified against other published
Z Table t Table Chi-Square Table F Tables for:
Standard Normal (Z) Table
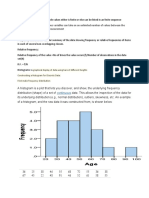
The Standard Normal distribution is used in various hypothesis tests including tests on single means, the difference between two means, and t proportions. The Standard Normal distribution has a mean of 0 and a standard deviation of 1. The animation above shows various (left) tail are distribution. For more information on the Normal Distribution as it is used in statistical testing, see Elementary Concepts. See also, As shown in the illustration below, the values inside the given table represent the areas under the standard normal curve for values z-score. For example, to determine the area under the curve between 0 and 2.36, look in the intersecting cell for the row labeled 2.30 0.06. The area under the curve is .4909. To determine the area between 0 and a negative value, look in the intersecting cell of the row sums to the absolute value of the number in question. For example, the area under the curve between -1.3 and 0 is equal to the area under between 1.3 and 0, so look at the cell on the 1.3 row and the 0.00 column (the area is 0.4032). Area between 0 and z
0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.0 0.0000 0.0040 0.0080 0.0120 0.0160 0.0199 0.0239 0.0279 0.0319 0.0359 0.1 0.0398 0.0438 0.0478 0.0517 0.0557 0.0596 0.0636 0.0675 0.0714 0.0753 0.2 0.0793 0.0832 0.0871 0.0910 0.0948 0.0987 0.1026 0.1064 0.1103 0.1141 0.3 0.1179 0.1217 0.1255 0.1293 0.1331 0.1368 0.1406 0.1443 0.1480 0.1517
Nonparametric Statistics Partial Least Squares Power Analysis Process Analysis Quality Control Charts Reliability / Item Analysis SEPATH (Structural eq.)
0.4 0.1554 0.1591 0.1628 0.1664 0.1700 0.1736 0.1772 0.1808 0.1844 0.1879 0.5 0.1915 0.1950 0.1985 0.2019 0.2054 0.2088 0.2123 0.2157 0.2190 0.2224 0.6 0.2257 0.2291 0.2324 0.2357 0.2389 0.2422 0.2454 0.2486 0.2517 0.2549 0.7 0.2580 0.2611 0.2642 0.2673 0.2704 0.2734 0.2764 0.2794 0.2823 0.2852 0.8 0.2881 0.2910 0.2939 0.2967 0.2995 0.3023 0.3051 0.3078 0.3106 0.3133 0.9 0.3159 0.3186 0.3212 0.3238 0.3264 0.3289 0.3315 0.3340 0.3365 0.3389 1.0 0.3413 0.3438 0.3461 0.3485 0.3508 0.3531 0.3554 0.3577 0.3599 0.3621
http://www.statsoft.com/textbook/distribution-tables/
5/16/2012
Vous aimerez peut-être aussi
- 2 Presenting Data in Charts and TablesDocument35 pages2 Presenting Data in Charts and TablesAdha Estu RizqiPas encore d'évaluation
- Chapters1-3 StaticDocument7 pagesChapters1-3 StaticsarkarigamingytPas encore d'évaluation
- Statistics and ProbabilityDocument253 pagesStatistics and Probabilityanirudhsaxena865Pas encore d'évaluation
- Statistics and ProbabilityDocument196 pagesStatistics and ProbabilitySiddharth GuptaPas encore d'évaluation
- Selected Topics in Graphical Analytic Techniques: Brief Overviews of Types of GraphsDocument30 pagesSelected Topics in Graphical Analytic Techniques: Brief Overviews of Types of GraphsmouperPas encore d'évaluation
- Click On Tabs On The Bottom To Switch To Different Tests: Chi Square TestDocument23 pagesClick On Tabs On The Bottom To Switch To Different Tests: Chi Square Testnafis022Pas encore d'évaluation
- VisualizationDocument27 pagesVisualizationsbapoorvaa1Pas encore d'évaluation
- Difference Between (Median, Mean, Mode, Range, Midrange) (Descriptive Statistics)Document11 pagesDifference Between (Median, Mean, Mode, Range, Midrange) (Descriptive Statistics)mahmoudPas encore d'évaluation
- ToleranceAnalysis 160613 01ADocument4 pagesToleranceAnalysis 160613 01Amedi38Pas encore d'évaluation
- A New Graphic For One-Way ANOVA: Data-Based Contrasts. Indeed, There Appears To Be One Distinctive Approach ToDocument12 pagesA New Graphic For One-Way ANOVA: Data-Based Contrasts. Indeed, There Appears To Be One Distinctive Approach ToEdwin Johny Asnate SalazarPas encore d'évaluation
- Statistics - 1: Presentation of DataDocument37 pagesStatistics - 1: Presentation of Datanpk007Pas encore d'évaluation
- Chapter 1 Summary - Displaying and Describing Data DistributionsDocument3 pagesChapter 1 Summary - Displaying and Describing Data DistributionsshinymaterialsPas encore d'évaluation
- Analyze Descriptive Statistics Frequencies: SPSS PC Version 10: Frequency Distributions and CrosstabsDocument3 pagesAnalyze Descriptive Statistics Frequencies: SPSS PC Version 10: Frequency Distributions and CrosstabsSalman ButtPas encore d'évaluation
- Statistics Minitab - Lab 8: and Standard DeviationDocument5 pagesStatistics Minitab - Lab 8: and Standard DeviationAndrè Alejandro Mazuelos CarpioPas encore d'évaluation
- Assignment No:-01: Name:-Snehal - Satyavrat.Yadav ROLL - NO:-42Document12 pagesAssignment No:-01: Name:-Snehal - Satyavrat.Yadav ROLL - NO:-42poojaPas encore d'évaluation
- Unit 1.2Document4 pagesUnit 1.2Akash kumarPas encore d'évaluation
- Rtet Racho RicDocument10 pagesRtet Racho RicsulfitrahPas encore d'évaluation
- ES 01 Central and DispersionDocument21 pagesES 01 Central and DispersionTaimoor Hassan KhanPas encore d'évaluation
- Bstat 2Document14 pagesBstat 2Mamun RashidPas encore d'évaluation
- Use of Statistics by ScientistDocument22 pagesUse of Statistics by Scientistvzimak2355Pas encore d'évaluation
- Traverse SheetDocument61 pagesTraverse Sheetعامري اليPas encore d'évaluation
- TraverseXL V1 0Document55 pagesTraverseXL V1 0Prabesh AdhikariPas encore d'évaluation
- Standard Normal Curve Probability DistributionDocument4 pagesStandard Normal Curve Probability DistributionLiam CheongPas encore d'évaluation
- Plots, Curve-Fitting, and Data Modeling Using Microsoft Excel (How To Plot Data)Document11 pagesPlots, Curve-Fitting, and Data Modeling Using Microsoft Excel (How To Plot Data)Tim FooPas encore d'évaluation
- Graphical Representation of DataDocument7 pagesGraphical Representation of Datatazim18Pas encore d'évaluation
- Solution Manual For Statistics For The Behavioral Sciences 10th EditionDocument38 pagesSolution Manual For Statistics For The Behavioral Sciences 10th Editiongingivalestrich6ptm100% (19)
- Solution Manual For Statistics For The Behavioral Sciences 10th EditionDocument38 pagesSolution Manual For Statistics For The Behavioral Sciences 10th Editionfootfleececyud5100% (14)
- Probability+&+Statistics FormulasDocument50 pagesProbability+&+Statistics Formulaschetandk47Pas encore d'évaluation
- Histogram & Box PlotDocument6 pagesHistogram & Box PlotAre MeerPas encore d'évaluation
- Understanding Z-Scores: Many Different Normal DistributionsDocument6 pagesUnderstanding Z-Scores: Many Different Normal Distributionslope pecayoPas encore d'évaluation
- Data GraphicsDocument4 pagesData GraphicsprojectboyPas encore d'évaluation
- 10 Inference For Regression Part2Document12 pages10 Inference For Regression Part2Rama DulcePas encore d'évaluation
- Variance and Standard DeviationDocument15 pagesVariance and Standard DeviationSrikirupa V Muraly100% (3)
- 2/ Organizing and Visualizing Variables: DcovaDocument4 pages2/ Organizing and Visualizing Variables: DcovaThong PhanPas encore d'évaluation
- Test 1 NotesDocument6 pagesTest 1 NotesDan PhamPas encore d'évaluation
- Cofactor StatisticsDocument27 pagesCofactor StatisticsAdam100% (1)
- Data Analysis-Univariate & BivariateDocument9 pagesData Analysis-Univariate & BivariateMeenakshi ChoudharyPas encore d'évaluation
- Unit - 2 BRM PDFDocument9 pagesUnit - 2 BRM PDFmalavika nairPas encore d'évaluation
- How To Plot Data Mar2012Document11 pagesHow To Plot Data Mar2012Tim FooPas encore d'évaluation
- Graphs and ChartsDocument13 pagesGraphs and ChartsAwais BangashPas encore d'évaluation
- Imran Masih Solved 1167109 2ndDocument7 pagesImran Masih Solved 1167109 2ndimran.info4582Pas encore d'évaluation
- Introduction To Descriptive Statistics I: Sanju Rusara Seneviratne MbpssDocument35 pagesIntroduction To Descriptive Statistics I: Sanju Rusara Seneviratne MbpssVincent Raj KumarPas encore d'évaluation
- Unit 2 Chapter 2 Notes - StatisticsDocument4 pagesUnit 2 Chapter 2 Notes - StatisticsVhuhwavhoPas encore d'évaluation
- Deciles and PercentilesDocument52 pagesDeciles and PercentilesShaik Mujeeb RahamanPas encore d'évaluation
- Business Statistics: Qualitative or Categorical DataDocument14 pagesBusiness Statistics: Qualitative or Categorical DataSweety 12Pas encore d'évaluation
- Data Summary and Presentation 1Document39 pagesData Summary and Presentation 1ZC47Pas encore d'évaluation
- NotesDocument44 pagesNotesAamna RazaPas encore d'évaluation
- Instructors:: Prof. V.E Efeovbokhan, Dr. Adegoke, and Engr. D. E. BabatundeDocument27 pagesInstructors:: Prof. V.E Efeovbokhan, Dr. Adegoke, and Engr. D. E. BabatundePreciousPas encore d'évaluation
- X Bar&RchartDocument9 pagesX Bar&RchartPramod AthiyarathuPas encore d'évaluation
- The Normal Distribution PDFDocument12 pagesThe Normal Distribution PDFIsraelPas encore d'évaluation
- Chap 003Document50 pagesChap 003AlondraPas encore d'évaluation
- Assignment: MBA 1 Semester Statistics For Management (Mb0040)Document10 pagesAssignment: MBA 1 Semester Statistics For Management (Mb0040)Niranjan VijayaraghavanPas encore d'évaluation
- Data Visualization & Data Exploration - Unit IIDocument26 pagesData Visualization & Data Exploration - Unit IIpurusingh23Pas encore d'évaluation
- This Excel File Will Allow You To Do The Following Tests: Chi-Square Test T-Test Paired T-Test Regression Simpson's Diversity IndexDocument40 pagesThis Excel File Will Allow You To Do The Following Tests: Chi-Square Test T-Test Paired T-Test Regression Simpson's Diversity IndexDimitrios MilionisPas encore d'évaluation
- Interpreting SPSS OutputDocument2 pagesInterpreting SPSS Outputhayati5823100% (1)
- Chapter 3 - Data Visualization Chapter 4 - Summary StatisticsDocument38 pagesChapter 3 - Data Visualization Chapter 4 - Summary StatisticsjayPas encore d'évaluation
- Basic Functions of ExcelDocument76 pagesBasic Functions of Excelnikita aggarwalPas encore d'évaluation
- 05 Handout 1Document13 pages05 Handout 1raulPas encore d'évaluation
- Trifocal Tensor: Exploring Depth, Motion, and Structure in Computer VisionD'EverandTrifocal Tensor: Exploring Depth, Motion, and Structure in Computer VisionPas encore d'évaluation
- Image Histogram: Unveiling Visual Insights, Exploring the Depths of Image Histograms in Computer VisionD'EverandImage Histogram: Unveiling Visual Insights, Exploring the Depths of Image Histograms in Computer VisionPas encore d'évaluation
- Technical Report WritingDocument21 pagesTechnical Report WritingMalik JalilPas encore d'évaluation
- Practical Interpretation and Application of Exoc Rine Panc Rea Tic Tes Ting in Small AnimalsDocument20 pagesPractical Interpretation and Application of Exoc Rine Panc Rea Tic Tes Ting in Small Animalsl.fernandagonzalez97Pas encore d'évaluation
- Activity 2Document2 pagesActivity 2cesar jimenezPas encore d'évaluation
- Chem31.1 Experiment 2Document28 pagesChem31.1 Experiment 2Mia FernandezPas encore d'évaluation
- BD9897FS Ic DetailsDocument5 pagesBD9897FS Ic DetailsSundaram LakshmananPas encore d'évaluation
- Sample ProposalDocument2 pagesSample ProposaltoupiePas encore d'évaluation
- Access PHD Thesis British LibraryDocument4 pagesAccess PHD Thesis British Libraryafcmausme100% (2)
- BSP Training MatrixDocument2 pagesBSP Training MatrixLeonisa V. BraganzaPas encore d'évaluation
- Elements of Visual Design in The Landscape - 26.11.22Document15 pagesElements of Visual Design in The Landscape - 26.11.22Delnard OnchwatiPas encore d'évaluation
- MNLG 4Document2 pagesMNLG 4Kanchana Venkatesh39% (18)
- Durability Problems of 20 Century Reinforced Concrete Heritage Structures and Their RestorationsDocument120 pagesDurability Problems of 20 Century Reinforced Concrete Heritage Structures and Their RestorationsManjunath ShepurPas encore d'évaluation
- Sosa Ernest - Causation PDFDocument259 pagesSosa Ernest - Causation PDFtri korne penal100% (1)
- Lesson Plan (Speaking Skills)Document7 pagesLesson Plan (Speaking Skills)Nurul Fathiah Zulkarnain100% (1)
- 1654557191.969365 - Signed Contract Application 212143Document11 pages1654557191.969365 - Signed Contract Application 212143ella may sapilanPas encore d'évaluation
- LITERATURE MATRIX PLAN LastimosaDocument2 pagesLITERATURE MATRIX PLAN LastimosaJoebelle LastimosaPas encore d'évaluation
- Fabre, Intro To Unfinished Quest of Richard WrightDocument9 pagesFabre, Intro To Unfinished Quest of Richard Wrightfive4booksPas encore d'évaluation
- Skin DseDocument9 pagesSkin DsePapitas FritasPas encore d'évaluation
- Simple Linear Equations A Through HDocument20 pagesSimple Linear Equations A Through HFresgPas encore d'évaluation
- Paper 2Document8 pagesPaper 2Antony BrownPas encore d'évaluation
- The Students Ovid Selections From The Metamorphoses by Ovid, Margaret Worsham MusgroveDocument425 pagesThe Students Ovid Selections From The Metamorphoses by Ovid, Margaret Worsham MusgroveMiriaam AguirrePas encore d'évaluation
- Development Communication Theories MeansDocument13 pagesDevelopment Communication Theories MeansKendra NodaloPas encore d'évaluation
- God As CreatorDocument2 pagesGod As CreatorNeil MayorPas encore d'évaluation
- 2016 01 15 12 00 22 PDFDocument26 pages2016 01 15 12 00 22 PDFABHIJEET SHARMAPas encore d'évaluation
- Deeg Palace Write-UpDocument7 pagesDeeg Palace Write-UpMuhammed Sayyaf AcPas encore d'évaluation
- HSE Matrix PlanDocument5 pagesHSE Matrix Planवात्सल्य कृतार्थ100% (1)
- 2 Beginner 2nd GradeDocument12 pages2 Beginner 2nd GradesebPas encore d'évaluation
- Caisley, Robert - KissingDocument53 pagesCaisley, Robert - KissingColleen BrutonPas encore d'évaluation
- Berms For Stablizing Earth Retaining Structures: Youssef Gomaa Youssef Morsi B.SC., Civil EngineeringDocument212 pagesBerms For Stablizing Earth Retaining Structures: Youssef Gomaa Youssef Morsi B.SC., Civil EngineeringChan KPas encore d'évaluation
- Mohd Ali 17: By:-Roll NoDocument12 pagesMohd Ali 17: By:-Roll NoMd AliPas encore d'évaluation