Académique Documents
Professionnel Documents
Culture Documents
Vibrations in Engineering: Faculty of Civil Engineering and Applied Mechanics
Transféré par
vuhoangdai90Titre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Vibrations in Engineering: Faculty of Civil Engineering and Applied Mechanics
Transféré par
vuhoangdai90Droits d'auteur :
Formats disponibles
Vibrations in Engineering
Lecture note by Dr. Sc. Nguyen Hoai Son
Faculty of Civil Engineering and Applied Mechanics
Earthquake-induced Vibration Failure:
Kobe, Japan 1995
CHAPTER I
one degree of freedom systems
Good luck on this course, I hope that will be obtain many question and be able
discuss any this all. Best wishes for your future career, and be sure to visit our
faculty!
Desirable
MRI
Ultrasound
Atomic Force Microscopy
Undesirable
See longer videos on YouTube and an even longer one on:
http://www.archive.org/details/SF121
Earthquake-induced Vibrational
Failure:
Kobe, Japan 1995
Vibration Control and Isolation
With and Without Isolation
Scope of Lectures
1-DOF (degree of freedom) systems only
FREE Vibration provide initial conditions and let go
Damped
Undamped
FORCED Vibration (harmonic only) Continuously force the
system with an oscillating force or motion
Scope of Lectures
External Forcing
Base Excitation
Rotor Excitation
Future Courses
Multi-DOF systems
Continuous (Infinite
DOF) systems
Idealised Elements in Vibration Analysis
Storing Potential and Kinetic Energy:
Lumped Masses
Usually idealisations of real objects
e.g.
Dissipating Energy
Dashpots (viscous damping)
Springs
k
k
dF
dx
= = constant if linear
F kx = if linear
F cx =
Force depends on VELOCITY
Push quickly big resistance
Let go it does not spring back, so
(mechanical) energy is not stored,
it is lost to heat etc.
A true dashpot consists of a plunger inside a fluid-filled cylinder.
c then depends on the fluid viscosity and plunger dimension
If A~1 cm
2
:
c
air
=2.6x10
-8
N/(m/s)
c
water
=10 x c
air
c
oil
=10
3
x c
water
c
maple syrup
=10 x c
oil
c
choc syrup
=10 x c
maple syrup
c
peanut butter
=10 x c
choc syr
(Other types of damping described by different equations exist, e.g. Coulomb
or frictional damping, material hysteresis etc.)
x
ST
o
Equilibrium position
Sloped
Equation of Motion for Undamped 1DOF system
Measure x from static equilibrium position NOT the unstretched position!!
( )
x x
F ma =
kx mx =
( )
x x
F ma =
( )
ST
k x mg mx o + + =
Eqn of Motion
Vertical Horizontal
Eqn of Motion
mg
( )
ST
k x o +
N
Eqn of Motion
( )
x x
F ma =
( ) sin
ST
k x mg mx o u + + =
kx mx =
kx mx =
kx
If you measure x from the static equilibrium position:
1. No need to show static spring force or gravity force on the FBD (they
cancel in the equation of motion)
2. The equation of motion is always the same regardless of the orientation
of the system
How about a problem like this?
Find the equation of motion for the system
Try including the gravity and static spring
forces first.
1
( )
ST
k x o +
mg
N
mg
1
x
ST
o
Equilibrium position
/ 2
ST
o
2 1
/ 2 x x =
FBD 1
( )
1 1
( ) sin
ST ST ST
T T k x mg m x o u o
'
+ + = + (1)
1
2 2
2
ST
ST
x
T T mg m
o +
'
+ = (2)
ST
T T T' = +
2 2 2
ST
T T T' = +
1
4
x
T m
'
=
(2)
FBD 2
1 1
5
0
4
m
x kx + =
(1)&(2)
T is the dynamic
Part of T
Get same answer if only include the dynamic forces and leave out the static
equilibrium forces
1
kx
1
x
ST
o
Equilibrium position
/ 2
ST
o
2 1
/ 2 x x =
FBD 1
FBD 2
1 1
T kx mx
'
= (1)
1
2
2
x
T m
'
=
(2)
T'
2T'
1
4
x
T m
'
=
(2)
1 1
5
0
4
m
x kx + =
(1)&(2)
kx
If you measure x from the static equilibrium position:
1. No need to show static spring force or gravity force on the FBD (they
cancel in the equation of motion)
2. The equation of motion is always the same regardless of the orientation
of the system
3. If there are other forces besides the spring and gravity forces need only
show dynamic portion (actual force minus value at static equilibrium)
kx
T'
ST
T T T
'
=
Solving the Equation of Motion
mx kx
+ =0
Homogeneous 2nd order, linear, ordinary differential equation with constant
coefficients (sing along to teeny, weeny, itsy-bitsy if it makes you feel better)
2nd order 2 arbitrary constants, which become fixed if specify initial condns
( )
t
x t Ce
= Standard trial soln (why?):
(1)
Plug into (1):
2
0
t t
mC e kCe
+ =
2
0 m k + =
C=0 would be a trivial
solution so:
Characteristic Equation
n
k k
i i
m m
e = + = + = + Soln of Char Eqn:
n
k
m
e = (letting: )
So, both: x t Ce x t C e
i t i t
n n
( ) ( ) = =
1 2
e e
AND
are solutions to (1)
By Principle of Superposition for linear systems
x t Ce C e
i t i t
n n
( ) = +
1 2
e e
is also a solution to (1)
Solving the Equation of Motion
mx kx
+ =0
(1)
x t Ce C e
i t i t
n n
( ) = +
1 2
e e
is the general solution to (1) since it has two arbitrary constants
In fact:
1 2
and C C
e i e i
i i u u
u u u u = + =
cos sin & cos sin Now, since:
where A, B are (different) arbitrary constants:
1 2
1 2
( )
A C C
B i C C
= +
(
(
=
Finally, the two arbitrary constants become fixed if we specify two
initial conditions (e.g. the initial position and velocity of the mass):
0 0
( 0) and ( 0) x t x x t x = = = =
The general solution can also be written as:
x t A t B t
n n
( ) cos sin = + e e (2)
Putting these in (2) and the derivative of (2) respectively, determines
the arbitrary constants:
0
A x =
0
n
x
B
e
=
Solving the Equation of Motion
mx kx
+ =0
(1)
n
k
m
e = x t x t
x
t
n
n
n
( ) cos
sin = +
0
0
e
e
e
The general solution to (1) is thus:
( )
which can be re-written finally (really this time!) as:
( )
( ) sin
n
x t X t e = +
2
2
0
0
n
x
X x
e
| |
= +
|
\ .
where:
1 0
0
tan
n
x
x
e
| |
=
|
\ .
and
0
A x =
0
n
x
B
e
=
What does the solution look like?
( )
( ) sin
n
x t X t e = +
2
2
0
0
n
x
X x
e
| |
= +
|
\ .
Period:
2
n
t
t
e
= (seconds)
Frequency:
n
e
(rads/s)
2
n
n
f
e
t
=
Or:
(Hz or cycles
per second)
(phase angle)
1 0
0
tan
n
x
x
e
| |
=
|
\ .
n
Note: the oscillation is about the static
equilibrium position
x
ST
o
Equilibrium position
Note: though we dont normally show the
static spring and gravity forces, these forces
CAN be used to find e
n
89.5
ST
mm o =
Man, mass 90kg steps on end
If he initiates an oscillation, what
would period of oscillation be?
Diving board acts like a spring with
some effective k
90(9.81)
9865 /
0.0895
ST
mg
k N m
o
= = =
9865
10.47 /
90
n
k
rads s
m
e = = =
ST
ko
mg
FBD
n
ST
g
e
o
= Or find, without getting k, from:
2
n
t
t
e
= = 0.60 seconds
Combining Springs
Springs in Series
Section at 1 and 2. What quantity is the same in both springs?
Force or displacement?
Force
F k k = =
1 1 2 2
o o So:
o o o = +
1 2
Total displacement:
replace with
eq
k
(equivalent spring)
F
k
F
k
F
k
eq
= +
1 2
Or:
1 1 1
1 2
k k k
eq
= + So:
k
k k
k k
eq
=
+
1 2
1 2
Or:
1 1 1 1
1 2
k k k k
eq n
= + ...
n springs:
Combining Springs
Section at 1. What quantity is the same in both springs? Force
or displacement?
Displacement
replace with
eq
k
(equivalent spring)
Springs in Parallel
(assume mass is
constrained to stay
horizontal) So: o o o
1 2
= =
Total force on mass:
F F F
1 2
+ =
Or:
1 2 eq
k k k o o o + =
So: k k k
eq
= +
1 2
n springs:
k k k k
eq n
= + +
1 2
.....
Which equation (series or parallel) applies to
these two springs?
(assume they have different stiffnesses)
Rotational Oscillation (e.g. Pendulum)
O O
M I o =
sin
O
mgL I u u =
u IF: small, then sinu u ~
So: 0
O
mgL
I
u u + =
mx kx
+ =0
Just like:
( )
( ) sin
n
t t u e = O +
Solution:
n
O
mgL
I
e =
with:
Changing I
O
changes period of motion (how you set a grandfather clock)
Energy Methods
Energy Methods can also be used to find the equation of motion
Potential Energy - Spring
( )
2 1
2
spr ST
V k x o = +
Potential Energy - Mass
sin
g
V mgx u =
Kinetic Energy Mass (system)
2
1
2
T mx =
( )
sin 0
ST
k x x mgx mxx o u + + =
0 x =
for all time would be a trivial solution, so:
0 mx kx + =
as before
( )
0 x mx kx + = or:
x
ST
o
Equilibrium position
e.g.: Sloped case:
( )
0
d T V
dt
+
= Conservative forces
Gravity PE Datum used here
(at equilibrium position)
Energy Methods - Aside
Note: you get the same answer if you assume:
2
1
2
spr
V kx =
0
g
V =
Actually the above is not really right (despite what the book says!). It might seem
as if you are just shifting the potential energy datums for the spring and gravity,
but actually you are ALSO saying the gravitational potential energy is zero
throughout the problem this clearly cannot be since the height of the mass
varies. So why does it give you the right answer?
Well it is the derivative of T+V that gives you the equation of motion.
1 2
U T = A
Recall: (work done = change in KE)
1 2
U V = A
and, in a conservative system: (work done = - (change in PE))
T V A = A So, in a conservative system:
dV dU
dt dt
= Thus
i.e. it is [ (rate of work done being by the forces)] we are
using in our derivation of the equation of motion.
which (dividing by dt) is the same eqn used on the previous slide:
( )
0
d T V
dt
+
=
ST
k x o Rate of work done being by the STATIC part of spring force:
( sin ) mg x u
Rate of work done being done by the gravity force:
These always cancel, so it is ok to only use the dynamic part of the spring
potential energy, and leave out the gravitational potential energy for this purpose
k
m
R
O
I
O
Energy methods especially useful when masses translate and rotate and
system gets more complex, since terms add as scalars
x
The oscillation will be about this equilibrium
position, and we measure x and u from the
equilibrium position and take only the dynamic
portion of the spring potential energy and leave out
the gravitational potential energy:
There will be a static displacement of the mass
downwards and rotation of the pulley mass
ST
o
ST
u
2
1
2
V kx =
2 2
1 1
2 2
O
T mx I e = +
x
R
e =
2 2
2
1 1
constant
2 2
O
I
T V m x kx
R
(
+ = + + =
(
( )
2
0
O
d T V
I
m xx kxx
dt R
+
(
= + + =
(
2
0
O
I
m x kx
R
(
+ + =
(
So equation of motion is:
2
n
O
k
I
m
R
e =
+
And natural frequency is:
(check you get the same result if you
include the static portion of the
spring PE and the gravitational PE)
Prob 8/27
3kg blob of putty dropped 2m onto initially stationary 28kg
block. Block supported by four springs.
k for each spring is 800 N/m
Find x(t), where x is measured from initial position of block
After impact, have a 31kg mass bouncing on four parallel springs
4 4(800)
10.16 /
31
n
k
rad s
m
e = = =
So:
Does the system oscillate about the initial position of block? No!!
The added mass of the putty changes the equilibrium position by an amount Ao
ST
Ao
ST
is the additional static deflection that would occur if we added the putty gently
without causing any vibrations
(4 )
ST p
k m g o A =
From static equilibrium:
3(9.81)
0.0092
4(800)
ST
m o A = =
Note! m
p
(mass of putty only)
Prob 8/27
( )
( ) sin
n
x t X t e = +
2
2
0
0
n
x
X x
e
| |
= +
|
\ .
where:
1 0
0
tan
n
x
x
e
| |
=
|
\ .
and
The general solution for motion about the static equilibrium is:
This is the solution when x is measured from the static
equilibrium position:
But here we are measuring x from the original equilibrium
position of the block before we added the putty, so we will need
to add on 0.0092m at the end after we solve for x(t) given by (1).
Need initial velocity of system immediately after impact:
By conservation of momentum during the collision:
( )
p p b b p b
m v m v m m v
'
+ = + Before
After
2 2(9.81)(2) 6.264 /
p
v gh m s = = =
By conservation of energy before the collision:
( )
(3)(6.264) 31 v
'
= So:
0.606 / v m s
'
=
(1)
Prob 8/27
( )
2
2
2
2
0
0
0.606
0.0092 0.0604
10.16
n
x
X x
e
| |
| |
= + = + =
|
|
\ .
\ .
So:
1 1
0
0
( 0.0092)(10.16)
tan tan 8.77
0.606
n
x
x
e
| |
| |
= = =
|
|
\ .
\ .
and
This is the initial velocity for the oscillation, i.e.
0.606 / v m s
'
=
0
0.606 / x m s =
What is:
0
x for the oscillation?!!
( )
( ) sin
n
x t X t e = +
Remember:
is the solution for
oscillation about the
equilibrium position
And the NEW equilibrium position is 0.0092 BELOW the
position where the putty hits the block (when the oscillation
starts), so
0
0.0092!! x =
( )
( ) 0.0092 0.0604sin 10.16 8.77 x t t = +
So, measuring x from the
original equilibrium position
(as in the picture):
Is this the same answer as in the book?
Prob 8/27
( )
( ) 0.0092 0.0604sin 10.16 8.77 x t t = +
Is this the same answer as in the book?
( )
( ) 0.0092 0.0092cos(10.16 ) 0.0597sin 10.16 x t t t = +
Answer in book:
( )
( ) 0.0092 sin 10.16 x t X t = + +
( ) ( )
( ) 0.0092 sin 10.16 cos cos 10.16 sin x t X t X t = + +
Want to re-write answer in book in the form:
Or:
(1)
(2)
Comparing (1) and (2):
sin 0.0092 X = cos 0.0597 X =
1
0.0092
tan 8.77
0.0597
| |
= =
|
\ .
( )
2
2
0.0092 0.0597 0.0604 X = + =
So:
So answer IS same as in the book
Damped Vibrations
Dashpots (viscous damping)
F cx =
Force depends on VELOCITY
Push quickly big resistance
Let go it does not spring back, so
(mechanical) energy is not stored,
it is lost to heat etc.
Introduce dashpots for damping. Recall:
Damped Vibrations Eqn of Motion
x again measured from the equilibrium
position, so no need to show gravity force.
kx cx mx =
( )
y y
F ma =
Eqn of Motion
0 mx cx kx + + =
Or:
2
2 0
n n
x x x ,e e + + =
n
k
m
e = Previously, introduced:
Now introduce:
2
n
c
m
,
e
=
Eqn of Motion can then be re-written as:
zeta - the damping ratio
Damped Vibrations - Solution
2
2 0
n n
x x x ,e e + + =
( )
t
x t Ce
= trial soln:
Plug into (1):
2 2
2 0
t t t
n n
C e C e Ce
,e e + + =
Characteristic Equation
(1)
2 2
2 0
n n
,e e + + =
2 2 2
2
2 4 4
1
2
n n n
n n
,e , e e
,e e ,
= =
Soln of Char Eqn:
2 2
1 1
1 2
( )
n n n
t t t
x t e Ce C e
, e , e ,e
(
= +
(
Generally,Two solns are combination of the two:
x t Ce C e
i t i t
n n
( ) = +
1 2
e e
(Note, the undamped soln : Falls out if ) 0 , =
Damped Vibrations Possible Cases
1 2
1 2
( )
t t
x t C e C e
= +
, Can vary from 0 to can be positive, negative or zero
2
1 ,
so
(note: an effective negative damping ratio can occur in self-excited oscillations e.g.
Tacoma Narrows bridge or aircraft flutter. )
1 , >
( )
2
1
1
n
e , , = +
( )
2
2
1
n
e , , =
where:
Case 1: Overdamped
Both roots real & negative sum of exponentials form (non-oscillatory)
1 2
,
( )
1 2 1 2
( )
n n n
t t t
x t Ce C e C C e
e e e
= + = +
1 , = Case 2: Critically damped
This is not the general solution since
1 2
C C +
constitutes only 1 arbitrary constant
n
t
Cte
e
Turns out is also a solution in this specific case, so general soln is:
( )
1 2
( )
n
t
x t A At e
e
= +
Overdamped & Critically Damped Cases
( )
1 2
( )
n
t
x t A At e
e
= + is the critically damped solution
A critically damped system with
an initial displacement, velocity
or both, returns to equilibrium
faster than an overdamped
system
This is also exponentially form (eventually!), non-oscillatory
motion
Case 3: Underdamped Case
Both roots complex, so:
1 2
,
1 2
1 2
( )
t t
x t C e C e
= + ( )
2
1
1
n
e , , = +
( )
2
2
1
n
e , , =
where:
1 , <
x t e C e C e
n n n
t i t i t
( ) = +
,e , e , e
1
1
2
1
2 2
( )
( ) sin
n
t
d
x t Xe t
,e
e
= +
2
1
d n
e , e = where:
Expressions for X and can be found as before in terms of the initial conditions
(*)
(*) represents damping oscillatory motion
The (damped) natural frequency is which is different from
d
e
n
e
Case 3: Underdamped Case 1 , <
( )
( ) sin
n
t
d
x t Xe t
,e
e
= +
2
d
d
t
t
e
=
clear all;clc;
grid on;hold on;
m=1;k=36;c=1;zeta=0.0833;
aumega_n=sqrt(k/m);
aumega_d=sqrt(1-zeta^2)*aumega_n;
t=0:0.01:4;
mu=-zeta*aumega_n.*t;
e=exp(mu);
X=30;
x=X*e.*sin(aumega_d.*t+pi/2);
plot(t,x,'r','linewidth',2)
plot(t,X*e,'--','linewidth',1.2)
plot(t,-X*e,'--','linewidth',1.2)
( )
( )
1
2
1
1
2 2
sin
sin
n
n
t
d
t
d
Xe t
x
x Xe t
,e
,e
e
e
+
=
+
Experimental determination of ,: Apply initial disturbance and measure response
Successive values at t
1
and t
2
(separated by t
d
). From (*):
t t t
d
d
2 1 1
2
= + = + t
t
e
( ) ( ) ( )
2 1 1
sin sin 2 sin
d d d
t t t e e t e + = + + = +
( )
1
1
1
2
n
n d
n d
t
t
x e
e
x
e
,e
,e t
,e t
+
= =
1
2 2
2
2 2
ln
1 1
n d n
n
x
x
t t,
o ,e t ,e
e , ,
= = = =
Logarithmic Decrement is defined as:
Thus can measure Logarithmic Decrement and
determine , from:
( )
2
2
2
o
,
t o
=
+
Weight, W = 3400 lb (1lb=450g), 1ft=0.3048m
100 lb force applied 3 (2.54cm) displacement.
Let go. Rises, then falls to max of 0.5 below
the unloaded equilibrium posn on 1
st
rebound.
Treat as 1D problem, m
eq
= 0.5 truck mass.
Find , for the rear end and c for each
absorber.
Ex.1
One spring and
damper on each side
k
c c
k
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
0 2 4 6 8
Behaviour:
Static deflection gives k:
2 100 0
ST
ko =
Springs in parallel
100
200 /
2(0.25 )
lb
k lb ft
ft
= =
( )
2 2(200)
2.75 /
3400 / 2 / 32.2
n
k
rad s
m
e = = =
Response oscillatory underdamped, ,<1
3"
ln
0.5"
o
=
( )
2
2
0.274
2
o
,
t o
= =
+
2
n
c
m
,
e
=
By definition:
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
0 2 4 6 8
But have 2 dashpots here in parallel so:
2
2
n
c
m
,
e
=
c damping coefficient in one damper
n
c me , =
ln6 1.79 o = =
i.e.:
2
(3400 / 2)
(2.75 / )(0.274) 39.8 /
32.2 /
lbs
c rad s lb s ft
ft s
= =
So:
clear all;clc;
grid on;hold on;
k=200;zeta=0.274;
aumega_n=2.75;
aumega_d=sqrt(1-zeta^2)*aumega_n;
t=0:0.01:8;
mu=-zeta*aumega_n.*t;
e=exp(mu);
X=-3;
x=X*e.*sin(aumega_d.*t+pi/2);
plot(t,x,'r','linewidth',2)
Released from Initial position x
0
.and velocity x
0
=0.
Find overshoot displacement x
1
.
k = 108 N/m, c = 18 Ns/m, m = 3 kg
108
6 /
3
n
k
rad s
m
e = = =
First:
18 1
2 2(3)6 2
n
c
m
,
e
= = = Next:
Underdamped
2
1
d n
e , e =
( )
( ) sin
n
t
d
x t Xe t
,e
e
= +
Damped frequency:
General Solution:
Use initial conditions to find : and X
0
( 0) sin x t X x = = =
( ) ( )
( ) sin cos
n n
t t
n d d d
x t Xe t Xe t
,e ,e
,e e e e
= + + +
Differentiate x(t):
Ex.2
2
1 0.5 (6) 5.196 / rad s = =
clear all;clc;
grid on;hold on;
m=3;k=108;c=18;zeta=0.5;
aumega_n=sqrt(k/m);
aumega_d=sqrt(1-zeta^2)*aumega_n;
t=0:0.01:3;
mu=-zeta*aumega_n.*t;
e=exp(mu);
X=3;
x=X*e.*sin(aumega_d.*t+pi/3);
plot(t,x,'r','linewidth',2)
( ) ( )
( ) sin cos
n n
t t
n d d d
x t Xe t Xe t
,e ,e
,e e e e
= + + +
( 0) sin cos ...
n d
x t X X ,e e = = + =
0
tan
d
n
e
,e
=
5.196
tan 1.732
0.5(6)
= =
So: Or: So: 60 1.047 rads = =
0
sin X x = From before:
So:
0
1.155 X x =
d
t
/ 2
d
t
Want x
1
.
2
d
d
t
t
e
= From theory (or obviously):
So we want x(t) when:
( )
( ) sin
n
t
d
x t Xe t
,e
e
= +
d
t
t
e
=
0.5(6)
5.196
1 0
( ) 1.155 sin 5.196 1.0472
5.196
d
x x t x e
t
t t
e
| |
= = = +
|
\ .
1 0
0.163 x x =
So:
Damped Vibrations Summary
0 mx cx kx + + =
2
2 0
n n
x x x ,e e + + =
2
n
c
m
,
e
=
Equation of Motion
Or:
where:
Solution Possible Cases
1 2
1 2
( )
t t
x t C e C e
= +
1 , >
( )
2
1
1
n
e , , = +
( )
2
2
1
n
e , , =
where:
Case 1: Overdamped
Both roots real & negative sum of decaying exponentials (non-oscillatory)
1 2
,
1 , = Case 2: Critically damped
( )
1 2
( )
n
t
x t A At e
e
= +
For solving problems, use above equations as-is
Two roots identical real & neg. Non-oscillatory (slope changes sign at most ONCE).
For solving problems, use:
1 , < Case 3: Underdamped
( )
( ) sin
n
t
d
x t Xe t
,e
e
= +
2
1
d n
e , e =
For solving problems, use:
Oscillatory. Both roots complex.
In each case find the constants (e.g. C, A, X, ) from initial values of x and
x
Logarithmic Decrement
(Underdamped Case only)
1
2
ln
x
x
o =
( )
2
2
2
o
,
t o
=
+
Ex.3
Released from rest at x
0
= 6, when t=0
Find displacement at t = 0.5 sec, if:
(a) c = 12 lb-sec/ft and (b) c = 18 lb-sec/ft
12
1
2 2(3)2
n
c
m
,
e
= = = Next:
12
2 /
3
n
k
rad s
m
e = = =
1 / 12 / k lb in lb ft = = Convert k first:
96.6
3
32.2
m slugs = = So:
critically damped
( )
1 2
( )
n
t
x t A At e
e
= +
General solution for critically damped case is:
Use initial conditions to find A
1
and A
2
:
1
( 0) 0.5 x t A ft = = =
( )
1 2 2
( )
n n
t t
n
x t A At e Ae
e e
e
= + + Differentiate x(t):
1 2
( 0)
n
x t A A e = = + So:
2
( 0) (2)(0.5) 0 x t A = = + = Or:
2
1 A = So:
( )
2
( ) 0.5
t
x t t e
= +
1
( 0.5) 1 0.368 x t e ft
= = =
(a)
and: So:
from rest
x
0
= 6
Released from rest at x
0
= 6, when t=0
Find displacement at t = 0.5 sec, if:
(b) c = 18 lb-sec/ft
18
1.5
2 2(3)2
n
c
m
,
e
= = = overdamped
1 2
1 2
( )
t t
x t C e C e
= +
( )
2
1
1
n
e , , = +
( )
2
2
1
n
e , , =
where:
General solution for overdamped case is:
( )
2
1
(2) 1.5 1.5 1 0.764 = + =
Here:
( )
2
2
(2) 1.5 1.5 1 5.236 = =
0.764 5.236
1 2
( )
t t
x t C e C e
= + So:
Use initial conditions to find C
1
and C
2
:
1 2
( 0) 0.5 x t C C ft = = + =
Differentiate x(t):
0.764 5.236
1 2
( ) 0.764 5.236
t t
x t C e C e
=
So:
1 2
( 0) 0.764 5.236 0 x t C C = = =
(1)
(2)
(1)+(2)
1 2
0.585, 0.0854 C C = =
Over
Prob 8/43
0.764 5.236
( ) 0.585 0.0854
t t
x t e e
=
For part (b), the solution is:
( 0.5) 0.393 x t ft = =
So:
Released from rest at x
0
= 6, when t=0
( 0.5) 0.368 4.42" x t ft = = = Part (a) critically damped:
( 0.5) 0.393 4.72" x t ft = = =
Part (b) overdamped:
Compare answers:
x(t) is reducing fastest (from its initial value: x
0
) in part (a), i.e. system
approaches equilibrium faster when critically damped than when overdamped
Forced Vibrations
Free Vibrations: Provide initial conditions, then let go
Forced Vibrations (more common): Some external force is continuously
driving the system throughout time
The driving force can be periodic
(repeating), like in (a) and (b) in the
figure
Turns out that all the periodic
functions in (b) can be created by
forming infinite series of harmonic
functions (fourier analysis).
So the harmonic case is the place
we start (and finish in ENGIN 4)
or non-periodic like in (c)
External Forcing
Base Excitation
Types of Harmonic Forcing
Rotor Excitation
Resonance Sneak Preview
Resonance Sneak Preview
Resonance can have catastrophic effects
Nimitz Freeway Collapse, Oakland 1989
MRI
but is critical to many technologies
Atomic Force Microscopy
or just tuning in our
favourite station
Down to Work!
x again measured from the equilibrium
position, so no need to show gravity force.
0
sin kx cx F t mx e + =
( )
y y
F ma =
Eqn of Motion
0
sin mx cx kx F t e + + =
Or:
RHS not zero any more
A Non-homogeneous equation
2
0
2 sin
n n
F
x x x t
m
,e e e + + =
Or, with defined as before:
and
n
, e
Solution of Non-homogeneous equation has two parts:
( ) ( ) ( )
c p
x t x t x t = +
( ) :
c
x t
Complementary soln = solution with F
0
= 0; same as before (unforced)
( ) :
p
x t
Particular soln = ANY solution to the equation with
0
0 F =
Finding a Particular Solution
2 2
0
sin( ) 2 cos( ) sin( ) sin
n n
F
X t X t X t t
m
e e | ,e e e | e e | e + + =
( ) sin( )
p
x t X t e | =
Try:
i.e. we guess the displacement will be at the same frequency
as the force, but perhaps out of phase
( ) cos( )
p
x t X t e e | =
2
( ) sin( )
p
x t X t e e | = Then: and
Insert into equation of motion:
( ) ( )
( )
2
2
0
sin cos cos sin 2 cos cos sin sin
sin cos cos sin sin
n
n
X t t X t t
F
X t t t
m
e e | e | ,e e e | e |
e e | e | e
+ +
+ =
Expand the sin, cos terms:
2 2
0
cos 2 sin cos
n n
F
X X X
m
e | ,e e | e | + + =
2 2
sin 2 cos sin 0
n n
X X X e | ,e e | e | + =
Equate terms in : sin t e and terms in : cos t e
Finding a Particular Solution
2 2
sin 2 cos sin 0
n n
e | ,e e | e | + =
Solve (2) for |:
1
2 2
2
tan
n
n
,e e
|
e e
=
1
2
2
tan
1
n
n
e
,
e
|
e
e
=
| |
|
\ .
2 2
0
cos 2 sin cos
n n
F
X X X
m
e | ,e e | e | + + = (1)
(2)
A little manipulation of (1) gives:
0
2
2
2
2
1
2 1
n
n n
F
X
me
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
Or:
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
But notice that:
0 0
2
ST
n
F F
m k
o
e
= =
where:
ST
o
here, is the displacement that F
0
would cause if applied statically
(NOT the static displacement due to gravity!)
so:
The Complete Solution
( ) ( ) ( )
c p
x t x t x t = +
The complete solution is thus:
1 2
1 2
( ) sin( )
t t
x t C e C e X t
e | = + +
( )
( ) sin sin( )
n
t
tr d ss
x t X e t X t
,e
e e |
= + +
Recall: complementary soln takes on different forms for , <, = or > 1
for , < 1 (underdamped case), the complete solution can be written:
Regardless of whether , is <, = or > 1, the complementary soln always dies out
over time, whereas the particular solution exist.
Thus the complementary part of the solution is called the transient solution, and
the particular part of the solution is called the steady state solution. (hence the
subscripts tr and ss above).
Or:
The Complete Solution
The complete solution thus looks something like the following:
Force
Time
Displacement
Time
The steady-state vibrations are
at the forcing frequency and
persist. They are independent
of the initial conditions, and are
constant.
Transient vibrations at the natural frequency
occur at the start (superimposed on the SS
vibrations). The transient vibrations depend on
the initial conditions and die off if there is the
slightest bit of energy loss.
The Steady State Solution
The steady state solution is usually of most interest, so we focus
on that from now on.
( ) sin( )
ss
x t X t e | =
Here it is again:
1
2
2
tan
1
n
n
e
,
e
|
e
e
=
| |
|
\ .
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
0 0
2
ST
n
F F
m k
o
e
= =
where:
st
X
o
(often given the symbol M) is called the amplitude ratio or
magnification factor since it tells you how big the vibration
amplitude is, compared to if the same force was applied statically.
With no damping (, = 0) the amplitude ratio goes to infinity when
n
e e =
RESONANCE!!!
If the forcing frequency matches the natural frequency of the system, then
even for tiny forces, the displacement becomes infinite!
The Steady State Solution
With damping (, > 0) the amplitude ratio at
n
e e =
1
2
st
X
o ,
=
is
which is finite
We see that this is > 1 for , < 0.5 and < 1 for , > 0.5
For small values of , the amplitude ratio at resonance can still be very large.
( ) sin( )
ss
x t X t e | =
1
2
2
tan
1
n
n
e
,
e
|
e
e
=
| |
|
\ .
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
n
e e =
i.e. we get amplification at for , < 0.5
The Steady State Solution
How about |
n
e e =
when ? We see it = 90
o
, regardless of , !
The displacement is 90
o
out of phase with the force when
n
e e =
Significant? Well, look at the velocity:
( ) cos( )
ss
x t X t e e | =
So the velocity is ALWAYS 90
o
out of phase with the displacement (at any
forcing frequency) since sine is 90
o
out of phase with cosine.
( ) sin( )
ss
x t X t e | =
1
2
2
tan
1
n
n
e
,
e
|
e
e
=
| |
|
\ .
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
So when:
n
e e =
The velocity is IN-PHASE with the force!
When the mass is moving to the right, the force is to the right; when the mass is
moving to the left, the force is to the left (or up/down etc)
When we force the system at its natural frequency, energy is being added to
the system in the most efficient way possible; we are not fighting the natural
dynamics of the system
The Steady State Solution
We get the FULL picture by plotting the amplitude ratio and |
as a function of
n
e
e
This is called the frequency response.
st
X
M
o
=
Recall:
The Steady State Solution
We get the FULL picture by plotting the amplitude ratio and |
as a function of
n
e
e
This is called the frequency response.
Amplification
No amplification at high
n
e
e
No amplification at high
,
Little amplification at low
n
e
e
(WITH damping, the peak amplification
is not quite at )
n
e e =
st
X
M
o
=
Recall:
The Steady State Solution
Why dont we get amplification at low and high ?
n
e
e
Imagine the childs swing again.
Say we could somehow push with a sinusoidally varying force instead of short
duration impulse forces
The swing has a natural frequency it wants to swing at determined by the chain
length and g (i.e. gravity provides the spring in this case).
Imagine trying to force the swing to move at a very low frequency
When the swing starts to come back from its the highest point, you would actually
be holding your child up, trying to slow down his/her motion. i.e. you would be
wasting much of your energy, fighting gravity, or fighting the spring force.
Imagine trying to force the swing to move at a high frequency
When the swing is on its way up, you would have to slow it down, to get it to turn
around faster, i.e. if you leave it to its natural devices, it will take too long to get to
the top of its motion (the frequency will not be high enough). Again, you would be
wasting much of your energy, fighting gravity (actually fighting the inertia force
in this case).
The Steady State Solution
Why dont we get amplification at low and high ?
n
e
e
In both these cases, | is not = 90
o
, so the force is not in phase with the velocity
The only way NOT to waste energy fighting the spring and/or inertia forces in
the system, is to force the system at its natural frequency. This is the most
efficient way to put energy into the system.
Then the applied force is in phase with the velocity and in fact the only force it
needs to overcome is the damping force.
If no damping, there is nothing to fight and the displacement infinity!!
Ex.4
c = 2.4 lb-sec/ft
Determine the range of driving
frequencies for which X
ss
< 3
2
n
c
m
,
e
=
2
2.4 sec/
64.4
2 6
32.2 /
lb ft
lb
ft s
=
| |
|
\ .
72
6 /
2
n
k
rads s
m
e = = =
Get k and m in standard units:
6 / 72 / k lb in lb ft = =
2
64.4
2
32.2 /
lb
m slugs
ft s
= =
( )
2.4
0.1
2 2 6
, = =
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
What else do we need?
ST
o
0
5
0.0694 0.833"
72
ST
F
ft
k
o = = = =
2
2
2
0.833
3
2(0.1) 1
6 6
X
e e
= <
(
(
| | | |
+
(
| |
(
\ . \ .
(
Want:
2
2
2
2
0.833 (9) 2(0.1) 1
6 6
e e
(
(
| | | |
< +
( `
| | (
\ . \ .
(
)
Or:
2
2
2
2
0.833 (9) 2(0.1) 1
6 6
e e
(
(
| | | |
< +
( `
| | (
\ . \ .
(
)
2 2 2 4
0.833 0.01 9 0.5 0.006944 e e e < + +
2 2 2
0.006944( ) 0.49( ) 8.306 0 e e + >
2 2 2
0.006944( ) 0.49( ) 8.306 0 e e + = There are 2 solutions to the equality:
an inequality.
2
42.25 e =
2
28.31 e =
Or:
6.5 / rad s e = 5.32 / rad s e =
and:
and:
To satisfy the inequality, need:
6.5 / rad s e >
5.32 / rad s e <
Or:
Recall:
6 /
n
rads s e =
Safe zones
Relevant
curve
(,=0.1)
Redo for no damping case
6 /
n
rads s e = 0 , =
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
0.833"
ST
o =
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
2
2
1
1
st
n
X
o
e
e
=
(
| |
(
|
(
\ .
when no damping
Note: this actually has two solutions: (Use when )
n
e e <
And:
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
(Use when )
n
e e >
Using the two possible solutions in the above way keeps X positive for all e
Aside
a change in sign of X as e passes
through the natural frequency is the same
as a phase change of 180
o
since:
sin( ) sin( 180) X A X A = +
1
2
2
tan
1
n
n
e
,
e
|
e
e
=
| |
|
\ .
You can see this sudden phase change for the
undamped case in the frequency response plot
You can also see it if you examine the equation
for | around in the limit as , 0
n
e e =
( ) sin( )
ss
x t X t e | =
Another way to look at it is to use for all e
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
Since the time-varying steady state solution is:
(i.e. allow X to change sign as e
passes through the natural frequency)
In solving problems, the approach on the previous page is probably easiest
Prob 8/50 (continued)
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
6 /
n
rads s e = 0.833"
ST
o =
n
e e <
for
2
0.833
3
1
6
X
e
= <
| |
|
\ .
3" X < Want:
SO:
5.1 / rad s e <
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
n
e e >
for
2
0.833
3
1
6
X
e
= <
| |
|
\ .
SO:
6.78 / rad s e >
Comparing with the damped case in Prob 8/51, the range of unsafe frequencies
is larger here (unsurprisingly)
Rotor Excitation
Rotating machinery not always perfectly
balanced
e
Unbalanced. More mass
one side than other.
e.g. your cars wheels. Imperfectly
machined rotating disks etc
Leads to a sinusoidally-varying force
Model as an effective unbalanced mass m
with an effective eccentricity e, in a machine
of mass M
k
c
u=et
m
M
e
e
x(t)
k
c
u=et
m
M
e
e
x(t)
Rotor Excitation
y y
F ma =
2
2
( ) ( sin )
d
kx cx M m x m x e t
dt
e = + +
2
sin Mx cx kx me t e e + + =
Let M be the mass of the machine,
INCLUDING the eccentric mass
The non-rotating part of the mass has
position x, while the rotating part of the
mass has position:
sin x e t e +
Equation of motion:
2
0
F mee = Like before, but the forcing function is:
And the driven mass is M (not m), so:
n
k
M
e =
Note
k
c
u=et
m
M
e
e
x(t)
Rotor Excitation
2
sin Mx cx kx me t e e + + =
For external forcing with force F
0
, had:
was the static displacement caused by F
0
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
0
ST
F
k
o =
where:
ST
o
There isnt really a static displacement here since
only operates when the rotor is switched on
2
0
F mee =
But if we say is the static displacement that would occur if a static force
of value was applied to the system, we can use the same
equation to solve.
2
0
F mee =
ST
o
st
X
o
2
0
2
" "
ST
n
F me
k M
e
o
e
= = i.e. use above eqn for as before, if define:
Eqn of Motion
0
sin mx cx kx F t e + + =
2
0
2 sin
n n
F
x x x t
m
,e e e + + =
Solution:
( ) ( ) ( )
c p
x t x t x t = +
Forced Vibrations - Summary
Harmonic forcing only
Or:
1 2
1 2
( ) sin( )
t t
x t C e C e X t
e | = + +
Dies out Persists steady state
solution. Main interest.
0
sin F t e
The Steady State Solution
( ) sin( )
ss
x t X t e | =
1
2
2
tan
1
n
n
e
,
e
|
e
e
=
| |
|
\ .
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
0 0
2
ST
n
F F
m k
o
e
= =
where:
No damping case
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
2
2
1
1
st
n
X
o
e
e
=
(
| |
(
|
(
\ .
when no damping
Two solutions: (Use when )
n
e e <
And:
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
(Use when )
n
e e >
Using the two possible solutions in the above way keeps X positive for all e
(Alternative is to use the first equation for all e and allow X to change sign at e > e
n
but this can get a little confusing. What is actually happening is a phase change of
180 degrees which we are generally not that interested in.)
k
c
u=et
m
M
e
e
x(t)
Rotor Excitation
2
sin Mx cx kx me t e e + + =
Equation of motion:
2
0
F mee = Like before, but the forcing function is:
And the driven mass is M (not m), so:
n
k
M
e =
Solution as before, e.g.:
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
2
0
2
" "
ST
n
F me
k M
e
o
e
= = if define:
Note: M is the TOTAL
mass including m
Prob 8/69
0
1 m kg =
Total mass of the device = 10 kg
12 e mm =
i.e. M = 10 kg
Determine the two possible values of the equivalent spring stiffness k for the
mounting to permit the amplitude of the force transmitted to the fixed
mounting due to the imbalance to be 1500 N at a speed of 1800 rpm
2
0 0
2 F m ee =
2
0
2
2(1)(0.012)(1800 )
60
F
t
=
0
852.7 N F =
Finished? No!
This is the force driving the device.
If the device is connected to the fixed mounting through a spring, the force
transmitted to the mounting is:
T
F kx =
which has a maximum value of:
MAX
T
F kX = where X is the magnitude of the
displacement
Prob 8/69
We want the max force transmitted to be 1500 N, so there are two acceptable
solutions:
2
2
2
1
2 1
st
n n
X
o
e e
,
e e
=
(
(
| | | |
( +
( | |
(
\ . \ .
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
From before:
0
st
F
k
o
| |
=
|
\ .
Or, with no damping:
0
2
1
n
F
kX
e
e
=
| |
|
\ .
Thus:
2
852.7
1500
1
n
e
e
=
| |
|
\ .
2
852.7
1500
1
n
e
e
=
| |
|
\ .
(Aside: what actually happens is the transmitted force is in phase with forcing force
for and out of phase by 180
o
for )
n
e e <
n
e e >
or:
2
1
1
st
n
X
o
e
e
=
| |
|
\ .
(for )
n
e e < (for )
n
e e >
OR:
(for )
n
e e <
AND:
0
2
1
n
F
kX
e
e
=
| |
|
\ .
(for )
n
e e >
Prob 8/69
We get 823,100 / k N m =
2
852.7
1500
1
n
e
e
=
| |
|
\ .
2
852.7
1500
1
n
e
e
=
| |
|
\ .
or:
0.657
n
e
e
= 1.252
n
e
e
=
If the machine is to be run at 1800 rpm (=188.5 rads/s), then we need:
286.9 /
n
rad s e = 150.6 /
n
rad s e =
With M = 10 kg and
n
k
M
e =
226, 700 / k N m =
or:
or:
or:
i.e. we can choose a stiff spring and run the machine BELOW the natural freq
or we can choose a soft spring and run the machine ABOVE the natural freq
Force Transmission to Base
In the last problem, considered force
transmission to the ground (=kx)
With vibrating machinery this can be an
important consideration, so we mount such
equipment on isolating mounts
What is the force transmitted if the mount
has damping?
These are always 90
o
out of phase, so can represent the time-varying force
transmitted as:
F t kX t c X t
T
( ) sin cos = + e e e
It is the sum of the spring and dashpot
forces.
sin cos A B u u + In general, the maximum value over all u of :
is:
2 2
A B +
(prove!)
( ) ( )
2 2
T
F kX c X e = +
So the maximum force transmitted is:
k
c
u=et
m
M
e
e
x(t)
Force Transmission to Base
( ) ( )
2 2
T
F kX c X e = +
So the force transmission ratio is:
2
2
1
T
n
F kX
,e
e
| |
= +
|
\ .
0
2
2 2
/
2 1
n n
F k
X
e e
,
e e
=
(
( | |
( +
| (
(
\ .
( )
2
2
0 2
2
1 2
1 / 2
n
T
n
n
F
F
e
,
e
e
e e ,
e
| |
+
|
\ .
=
(
(
+
(
or:
From before:
k
c
u=et
m
M
e
e
x(t)
Force Transmission to Base
( )
2
2
0 2
2
1 2
1 / 2
n
T
n
n
F
F
e
,
e
e
e e ,
e
| |
+
|
\ .
=
(
(
+
(
Dont worry (be happy)
ST
X
o
A little different from the previous
plot we had for:
especially here:
Force Transmission to Base
For a force transmission ratio < 1
(i.e. vibration isolation), need:
Since the operating frequency
of the machine is probably
fixed, this means we need to
choose a soft enough spring
so the above is true
2
n
e e >
1 , =
0.5 , =
Also, in the isolation region ( ) a lower value of , lowers
2
n
e e >
T
F
However, the machine has to pass the resonant frequency on its way to its
operating speed from start-up, so , cannot be too low!
If the force transmission is not satisfactory with standard mount materials, another
option is to add weight to the machine, or mount it directly on another mass which is
then placed on the mounting pads. This will also bring down e
n
.
Harmonic Base Excitation
Base moves. How does the mass move?
e.g. earthquakes, hilly road acting on car etc.
Forces in the spring and dashpot are proportional
to the RELATIVE displacement and velocity
respectively
Harmonic Base Excitation
Two terms on RHS so a little different from before, but RHS can be re-written:
which is the same as before (apart from the o) if we let:
y y
F ma =
( ) ( ) k x y c x y mx =
Equation of motion:
mx cx kx ky cy + + = +
2 2
2 2
n n n n
x x x y y ,e e e ,e + + = +
2 2
2 sin 2 cos
n n n n
x x x Y t Y t ,e e e e ,e e e + + = +
( )
( ) ( )
2
2
2 2
2 2 sin
n n n n
x x x Y Y t ,e e e ,e e e o + + = + +
( )
( )
2
2
2
0
2
n n
F
Y Y
m
e ,e e = +
Or:
Or:
(dont worry about the
o - we could get it if
we wanted)
2
0 0
2
1 2
n n
F F
Y
k m
e
,
e e
| |
= = +
|
\ .
Harmonic Base Excitation
0
2
2 2
/
2 1
n n
F k
X
e e
,
e e
=
(
( | |
( +
| (
(
\ .
From before:
1
2
2
2
2 2
1 2
1 2
n
n n
X
Y
e
,
e
e e
,
e e
(
| |
(
+
|
(
\ .
(
=
(
| |
| | | |
(
| +
| |
| (
\ . \ .
\ .
So the displacement transmission ratio is:
( )
( )
2
2
2
0
2
n n
F
Y Y
m
e ,e e = +
Harmonic Base Excitation
1
2
2
2
2 2
1 2
1 2
n
n n
X
Y
e
,
e
e e
,
e e
(
| |
(
+
|
(
\ .
(
=
(
| |
| | | |
(
| +
| |
| (
\ . \ .
\ .
Displacement transmission ratio:
Notice this is exactly the same
expression as we got for the force
transmission ratio of a rotating
machine!! Even though this is a
different problem!
Not surprisingly the design criteria for limiting the displacement transmitted to the
mass here are the same as for limiting the force transmitted in the previous problem.
i.e. a soft enough spring, limited damping, and add mass if needed
Exactly same picture except y-axis is
X/Y instead of F
T
/F
0
this time:
Harmonic Base Excitation
soft spring
No isolation
Example
Car weighing 3000 lbs drives over a road with sinusoidal profile, as shown
k c
m
x(t)
16
s
33 ft
Design the suspension (i.e. pick k and c) so that:
1. The vibration amplitude of the car is < 14 at all speeds, and
2. The vibration amplitude of the car is < 4 at 55 mph
Example
2
sin
s
y Y
L
t
| |
=
|
\ .
Vibration amplitude < 14 at all speeds:
At speed v, distance is s=vt, and Y
= 8 = 2/3ft
Equation of road profile (base
motion):
2 2
sin
3 33
v
y t
t
| |
=
|
\ .
So the forcing frequency of the
base motion is:
k c
m
x(t)
16
s
33 ft
2
33
v t
e =
Use the graph:
0.375 , =
14
1.75
8
X
Y
< = at all speeds
0.375 , ~
gives about the best soln to
this criterion
Example
With , = 0.375:
2. Vibration amplitude < 4
at 55 mph
k c
m
x(t)
40 cm
s
10 m
Now solve for required k:
0.375 , =
So e
n
must be:
4
0.5
8
X
Y
< = at 55 mph
2 (80.67 / )
15.4 /
33
ft s
rad s
ft
t
e = =
5280
55 55 80.67 /
3600sec
ft
v mph ft s = = =
0.5
X
Y
<
2.1
n
e
e
>
when (approx)
15.4
7.33 /
2.1
n
rad s e < =
2
3000
(7.33) 5006 /
32.2
k lb ft
| |
= =
|
\ .
Example
Finally solve for c:
k c
m
x(t)
40 cm
s
10 m
2
n
c
m
,
e
=
So:
3000
2 2(0.375) (7.33 / ) 512.2 /
32.2
n
c m slugs rad s lb s ft , e
| |
= = =
|
\ .
2
(1 1 / ) slug lb s ft =
At what speed (approx) will the worst vibrations occur?
Prof. McCarthys first car
The ultra-cool Morris Minor
Even the name evokes excitement
On Irish roads, had natural frequency at about 45 mph a WHOLE lot of
shaking going on
Excellent excuse if stopped doing 55 mph in a 45 mph zone
Harmonic Base Excitation Motion
Relative to Base
Sometimes the motion relative to the base is of interest
( ) ( ) k x y c x y mx =
Introducing the relative displacement z = x y, the equation of
motion:
becomes, in terms of the relative displacement:
( ) kz cz m z y = +
mz cz kz my + + =
This case is dealt with on page 625 of the book with slight difference in
nomenclature:
sin
B
x b t e = sin y Y t e = Base motion: instead of:
x
z Relative motion variable: instead of:
2
n
Z
M
Y
e
e
| |
=
|
\ .
Writing the solution on page 625 in the current
nomenclature:
2
2
2
2
2 1
n
n n
Z
Y
e
e
e e
,
e e
| |
|
\ .
=
(
(
| | | |
( +
( | |
(
\ . \ .
Or:
Or:
Prob 8/61
The motion of the outer cart is varying sinusoidally
as shown.
For what range of e is the amplitude of the motion
of the mass m, relative to the cart less than 2b?
2
2
2
2
2 1
n
n n
Z
Y
e
e
e e
,
e e
| |
|
\ .
=
(
(
| | | |
( +
( | |
(
\ . \ .
2
2
1
n
n
Z
Y
e
e
e
e
| |
|
\ .
=
| |
|
\ .
when no damping
2
2
2
1
n
n
Z
Y
e
e
e
e
| |
|
\ .
=
(
| |
(
|
(
\ .
As before: there are two solutions:
(Use when )
n
e e <
And: (Use when )
n
e e >
2
2
1
n
n
Z
Y
e
e
e
e
| |
|
\ .
=
| |
|
\ .
Prob 8/61
We want
2
2
Z b
Y b
< =
2
2
2
1
n
n
e
e
e
e
| |
|
\ .
<
| |
|
\ .
2
3
n
e
e
<
2
2
2
1
n
n
e
e
e
e
| |
|
\ .
<
| |
|
\ .
2
n
e
e
>
n
e e <
for
n
e e >
for
Recitations as usual tomorrow (Wednesday)
No lecture this Thursday (May 1
st
)
No recitations next week
Review lecture next Tuesday (May 6
th
). Exam Wed May 7
th
, 9am.
Good luck on the final, best wishes for your future career, and
be sure to visit Ireland sometime!
HW13 due Friday 12:00. Hand in to Stephanie on 7
th
floor.
Problem 1.
Problem 2.
Problem 3.
A disk of mass m and radius R rolls w/o slip
while restrained by a dashpot with coefficient of
viscous damping c in parallel with a spring of
stiffness k. Derive the differential equation for
the displacement x(t) of the disk mass center C
and determine the viscous damping factor and
the frequency n of undamped oscillation.
Problem 4.
Problem 5.
Problem 6.
Problem 6.
Problem 6.
Problem 7.
Problem 7.
Problem 8.
Problem 8.
Problem 9.
The oscillatory characteristics of ships in
rolling motion depend on the position of the
metacenter, M, with respect to the center of
gravity, G. The metacenter, M, represents the
point of intersection of the line of action of the
buoyant force and the centerline of the ship,
and its distance, h, measured from G, is the
metacentric height, as shown. The position of
M depends on the shape of the hull, and, for
small values the angular inclination, q, of the
ship, h is independent of q. Show that the
period of motion for rolling is given by
t = p where J is the mass moment of inertia of
the ship about its axis of roll, and W is the
weight of the ship. Note: Unlike this problem,
in general the position of the roll axis is
unknown, and J is obtained from the period of
oscillation measured from a test of a model.
2
J
Wh
t t =
Solution
Problem 10
solution
A counter rotating eccentric weight exciter is used to
produce forced oscillation of a spring supported mass. By
varying the speed of rotation, a resonant amplitude of 0.60
cm was recorded. When the speed of rotation was
increased considerably above the resonant frequency, the
amplitude approached a fixed value of 0.08 cm. What was
the viscous damping ratio of the system?
Problem 11
solution
The figure represents a simplified arrangement
for a spring-supported vehicle traveling over a
rough road. Determine an equation for the
amplitude of motion for m as a function of road
speed. What is the worst road speed?
Problem 12
solution
Problem 13
solution
Problem 14
solution
Problem 15
solution
Problem 15
solution
e
M
m
e t
k/2 k/2
c
x
Problem 16
Estabished the vibration equation of
the system rotating unbalance as shown on
the side figure. Find the natural frequency,
damped frequency, damped ratio, Loga
decreament and response analysis.
Hint: You can sugguest for the data of problem
Problem 17.
Problem 18.
Vous aimerez peut-être aussi
- Time Response AnalysisDocument151 pagesTime Response AnalysisTushar GuptaPas encore d'évaluation
- FOPDT Model CharacterizationDocument6 pagesFOPDT Model CharacterizationHugo EGPas encore d'évaluation
- Chapter 2 System IInd Order ResponsesDocument38 pagesChapter 2 System IInd Order ResponsesAli AhmadPas encore d'évaluation
- MAE653 Sp10 Lesson06Document9 pagesMAE653 Sp10 Lesson06Edwin MachacaPas encore d'évaluation
- Continuous-Time Signals and SystemsDocument37 pagesContinuous-Time Signals and SystemsJoseph IbrahimPas encore d'évaluation
- The Zero-State Response Sums of InputsDocument4 pagesThe Zero-State Response Sums of Inputsbaruaeee100% (1)
- Ch-5 Time Res WebpageDocument48 pagesCh-5 Time Res WebpageTushar GuptaPas encore d'évaluation
- Solving Differential Equations via ConvolutionDocument13 pagesSolving Differential Equations via Convolutionlove_accPas encore d'évaluation
- Control Systems Unit-2 Time Response Analysis: Ms. P. Geethanjali Asst. Professor (SR) SelectDocument157 pagesControl Systems Unit-2 Time Response Analysis: Ms. P. Geethanjali Asst. Professor (SR) SelectVijay IndukuriPas encore d'évaluation
- Chapter 3 - MatlabDocument59 pagesChapter 3 - MatlabZe SaPas encore d'évaluation
- Lecture 22-23-24 Time Domain Analysis of 2nd Order SystemsDocument73 pagesLecture 22-23-24 Time Domain Analysis of 2nd Order SystemsPradeep Kumar Mehta100% (1)
- Solution To Homework Assignment 3Document2 pagesSolution To Homework Assignment 3Jackie DuanPas encore d'évaluation
- Experiment 1Document5 pagesExperiment 1HarshaPuttaguntaPas encore d'évaluation
- Project MatlabDocument10 pagesProject MatlabAbdullahPas encore d'évaluation
- Practical Class Two Matlab PracticalDocument6 pagesPractical Class Two Matlab PracticalPradyumnaSadgirPas encore d'évaluation
- Chapter 2Document31 pagesChapter 2Endalk SimegnPas encore d'évaluation
- LQRDocument5 pagesLQRdrjoshreePas encore d'évaluation
- Modeling in The Time Domain: Omisol and TarifeDocument28 pagesModeling in The Time Domain: Omisol and TarifeRovick Tarife0% (1)
- Matlab Differentiation Matrix SuiteDocument55 pagesMatlab Differentiation Matrix SuiteRaghav VenkatPas encore d'évaluation
- Indirect Adaptive ControlDocument24 pagesIndirect Adaptive Controlhondo tinemi dPas encore d'évaluation
- Report - Self Balancing BicycleDocument18 pagesReport - Self Balancing BicycleAniket PaithanePas encore d'évaluation
- A Digital-Based Optimal AVR Design of Synchronous Generator Exciter Using LQR TechniqueDocument13 pagesA Digital-Based Optimal AVR Design of Synchronous Generator Exciter Using LQR Technique3KaiserEPas encore d'évaluation
- Numerical Solution of Initial Value ProblemsDocument17 pagesNumerical Solution of Initial Value ProblemslambdaStudent_eplPas encore d'évaluation
- Design Control Systems State SpaceDocument42 pagesDesign Control Systems State SpaceBelayneh Tadesse100% (1)
- STAT515 S19 Final ReviewproblemssolutionsDocument13 pagesSTAT515 S19 Final ReviewproblemssolutionsElias BeyenePas encore d'évaluation
- Project:: Aditya Singh Vishnu Mhalaskar Akash Patil Deepak MauryaDocument21 pagesProject:: Aditya Singh Vishnu Mhalaskar Akash Patil Deepak MauryaBabbu MehraPas encore d'évaluation
- Adaptive Control 2Document30 pagesAdaptive Control 2kanchiPas encore d'évaluation
- SolutionsDocument66 pagesSolutionsEduardo Paulini VillanuevaPas encore d'évaluation
- Dynamic Characteristics of Sensors and Measurement SystemsDocument29 pagesDynamic Characteristics of Sensors and Measurement SystemsveenadivyakishPas encore d'évaluation
- MATLAB Linear Algebra FunctionsDocument15 pagesMATLAB Linear Algebra FunctionsAhmed HwaidiPas encore d'évaluation
- Files 2-Chapters 10 5 Transient Response SpecificationsDocument9 pagesFiles 2-Chapters 10 5 Transient Response SpecificationsYalemwork YargalPas encore d'évaluation
- 2015 Dynamic Modelling of A One Stage Spur Gear System and Vibration Based Tooth Crack Detection Analysis MohammedDocument13 pages2015 Dynamic Modelling of A One Stage Spur Gear System and Vibration Based Tooth Crack Detection Analysis MohammedPradeep Kumar MehtaPas encore d'évaluation
- Feedback Control Performance MeasuresDocument37 pagesFeedback Control Performance MeasuresmrkmatPas encore d'évaluation
- Dynamic System Stability ConceptsDocument25 pagesDynamic System Stability ConceptsAslı ÇakırPas encore d'évaluation
- 18 Adaptive ControlDocument7 pages18 Adaptive ControlFathi MusaPas encore d'évaluation
- Frequency Response Analysis and Design PDFDocument281 pagesFrequency Response Analysis and Design PDFfergusonisePas encore d'évaluation
- Dynamic Charactorstics of An InstrumentsDocument30 pagesDynamic Charactorstics of An InstrumentsDhinakaran VeemanPas encore d'évaluation
- Chapter 2.2 Response Ist Order SystemsDocument30 pagesChapter 2.2 Response Ist Order SystemsSyed AliPas encore d'évaluation
- HW - 2 Solutions (Draft)Document6 pagesHW - 2 Solutions (Draft)Hamid RasulPas encore d'évaluation
- Basic Simulation Lab: Amity UniversityDocument20 pagesBasic Simulation Lab: Amity UniversityAnonymous zpLxw2fwPas encore d'évaluation
- Signals and Systems Kuestion (EE) PDFDocument48 pagesSignals and Systems Kuestion (EE) PDFsanthoshPas encore d'évaluation
- Adaptive ControlDocument26 pagesAdaptive ControlKiran RavyPas encore d'évaluation
- Euler Method Matlab Code - BelajarDocument110 pagesEuler Method Matlab Code - BelajarM TaufikPas encore d'évaluation
- DynamicsDocument31 pagesDynamicsNagamani RajeshPas encore d'évaluation
- Modelling Discrete Time SystemsDocument6 pagesModelling Discrete Time SystemsSandeep KumarPas encore d'évaluation
- Dynamical Systems Method for Solving Nonlinear Operator EquationsD'EverandDynamical Systems Method for Solving Nonlinear Operator EquationsÉvaluation : 5 sur 5 étoiles5/5 (1)
- Spacecraft Attitude Control: A Linear Matrix Inequality ApproachD'EverandSpacecraft Attitude Control: A Linear Matrix Inequality ApproachPas encore d'évaluation
- Ordinary Differential Equations: 1971 NRL—MRC ConferenceD'EverandOrdinary Differential Equations: 1971 NRL—MRC ConferenceLeonard WeissPas encore d'évaluation
- Factorization Methods for Discrete Sequential EstimationD'EverandFactorization Methods for Discrete Sequential EstimationPas encore d'évaluation
- Vibrations and Waves Course NotesDocument125 pagesVibrations and Waves Course NotesMatthew BaileyPas encore d'évaluation
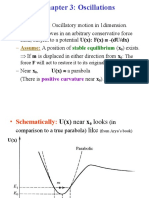
- Given A Potential Energy Graph, Oscillations Will Occur Between Turning Points Determined byDocument9 pagesGiven A Potential Energy Graph, Oscillations Will Occur Between Turning Points Determined byjdlawlisPas encore d'évaluation
- Harmonic Oscillation, Komang SuardikaDocument125 pagesHarmonic Oscillation, Komang SuardikaKomang SuardikaPas encore d'évaluation
- Structural DynamicsDocument99 pagesStructural DynamicsUtb Bjp100% (10)
- Pertemuan Ke 9 Get HarmonisDocument22 pagesPertemuan Ke 9 Get HarmonisPutri RamadiwarmanPas encore d'évaluation
- Elementary Tutorial: Fundamentals of Linear VibrationsDocument51 pagesElementary Tutorial: Fundamentals of Linear VibrationsfujinyuanPas encore d'évaluation
- VIBRATION TITLEDocument49 pagesVIBRATION TITLEMark Oliver BernardoPas encore d'évaluation
- Chapter 1 & 2 - Introduction To Vibrations and Single DOF SystemsDocument86 pagesChapter 1 & 2 - Introduction To Vibrations and Single DOF SystemsMohamad Faiz TonyPas encore d'évaluation
- June 2014 (R) MS - C2 EdexcelDocument20 pagesJune 2014 (R) MS - C2 EdexcelashiquePas encore d'évaluation
- Unit CIV2202: Surveying Topic 12: CurvesDocument22 pagesUnit CIV2202: Surveying Topic 12: CurvesNik M Farid100% (1)
- Differential Calculus With Matlab (2016)Document243 pagesDifferential Calculus With Matlab (2016)Julio CésarPas encore d'évaluation
- Applications - of - Trigonometric - Transformations KeyDocument12 pagesApplications - of - Trigonometric - Transformations KeyIGCSE NotesPas encore d'évaluation
- Applications & Interpretation - 1 Page Formula Sheet: IB Mathematics SL & HL - First Examinations 2021Document1 pageApplications & Interpretation - 1 Page Formula Sheet: IB Mathematics SL & HL - First Examinations 2021Zia Silver100% (1)
- 2014 RI Preliminary Exam Math Paper 1 ReviewDocument12 pages2014 RI Preliminary Exam Math Paper 1 ReviewcherylhzyPas encore d'évaluation
- The letter πDocument20 pagesThe letter πteddy_lan93Pas encore d'évaluation
- B.Tech CST R20Document212 pagesB.Tech CST R20ẞyed RehamanPas encore d'évaluation
- LV Capacitors Brochure Canada PDFDocument4 pagesLV Capacitors Brochure Canada PDFAmit PaulPas encore d'évaluation
- .Activity CombinedDocument30 pages.Activity CombinedTanishaPas encore d'évaluation
- Mathematics PQDocument20 pagesMathematics PQBERLIN XPas encore d'évaluation
- The Law of Cosines: For Any TriangleDocument5 pagesThe Law of Cosines: For Any TriangleaskmokoPas encore d'évaluation
- BindersDocument56 pagesBindersMSA ProductionPas encore d'évaluation
- 1 Laplace Transforms - NotesDocument16 pages1 Laplace Transforms - NotesSboPas encore d'évaluation
- Math 147 Forrest Notes PDFDocument416 pagesMath 147 Forrest Notes PDFRedwan MohammedPas encore d'évaluation
- Math Inverse Trignometric FunctionDocument5 pagesMath Inverse Trignometric FunctionShaku JoshiPas encore d'évaluation
- Its Class 8 Maths Model Question Terminal Paper 1Document2 pagesIts Class 8 Maths Model Question Terminal Paper 1Basanta AryalPas encore d'évaluation
- Methods12 2ed Full Part1Document318 pagesMethods12 2ed Full Part1kuoklukePas encore d'évaluation
- S.Y. B.sc. (Physics) Question BankDocument76 pagesS.Y. B.sc. (Physics) Question BankAmey KalePas encore d'évaluation
- Sheet 3 DerivativesDocument3 pagesSheet 3 DerivativeszakPas encore d'évaluation
- CLASS 10, INTRO TO TRIGONOMETRY, PPT, Module 1 BY 3Document22 pagesCLASS 10, INTRO TO TRIGONOMETRY, PPT, Module 1 BY 3Apoorv Arya100% (1)
- L2 Trigonometry of Right TrianglesDocument13 pagesL2 Trigonometry of Right TrianglesRyan Jhay YangPas encore d'évaluation
- Analytical Inversion of General Tridiagonal Matrices: Home Search Collections Journals About Contact Us My IopscienceDocument16 pagesAnalytical Inversion of General Tridiagonal Matrices: Home Search Collections Journals About Contact Us My IopscienceTruong HuynhPas encore d'évaluation
- MasteringPhysics - Assignment 7 - Forces Part OneDocument5 pagesMasteringPhysics - Assignment 7 - Forces Part OneStrange Sht100% (1)
- Differenting Useful Functions - CalculusDocument3 pagesDifferenting Useful Functions - CalculusRaghuSrinivasanPas encore d'évaluation
- (Mai 2.17) Sinusoidal ModelDocument10 pages(Mai 2.17) Sinusoidal Modelyara hazemPas encore d'évaluation
- AQA A Level Mathematics SpecificationDocument50 pagesAQA A Level Mathematics SpecificationastargroupPas encore d'évaluation
- Prelim Exam 4th Quarter Grade 9Document4 pagesPrelim Exam 4th Quarter Grade 9Vanessa PinarocPas encore d'évaluation
- Multiple Choice TrigonometryDocument3 pagesMultiple Choice TrigonometryMelanie Ibarra CarlosPas encore d'évaluation
- Fourier Transform TableDocument7 pagesFourier Transform TableGandhi NapitupuluPas encore d'évaluation