Académique Documents
Professionnel Documents
Culture Documents
Ac Drives
Transféré par
MSM7865Titre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Ac Drives
Transféré par
MSM7865Droits d'auteur :
Formats disponibles
AC DRIVES
The AC motor have a number of advantages :
Lightweight (20% to 40% lighter than equivalent DC motor)
Inexpensive
Low maintenance
The Disadvantages AC motor :
* The power control relatively complex and more expensive
There are two type of AC motor Drives :
1. Induction Motor Drives
2. Synchronous Motor Drives
AC motor Drives are used in many industrial and domestic
application, such as in conveyer, lift, mixer, escalator etc.
INDUCTION MOTOR DRIVES
Three-phase induction motor are commonly used in adjustable-speed
drives (ASD).
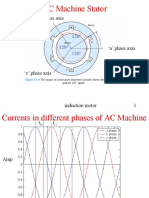
Basic part of three-phase induction motor :
Stator
Rotor
Air gap
Stator
Three-phase
windings
Rotor
Air gap
e T
Rotor windings
Three-
phase
supply
m
e
s
e
The stator winding are supplied with balanced three-phase AC voltage,
which produce induced voltage in the rotor windings. It is possible to
arrange the distribution of stator winding so that there is an effect of
multiple poles, producing several cycle of magnetomotive force (mmf) or
field around the air gap.
The speed of rotation of field is called the synchronous speed e
s
, which
is defined by :
p
s
e
e
2
=
s
is syncronous speed [rad/sec]
N
s
is syncronous speed [rpm]
p is numbers of poles
is the supply frequency [rad/sec]
f is the supply frequency [Hz]
N
m
is motor speed
Stator
Three-phase
windings
Rotor
Air gap
e T
Rotor windings
Three-
phase
supply
m
e
s
e
p
f
N
s
120
=
or
Stator
Three-phase
windings
Rotor
Air gap
e T
Rotor windings
Three-
phase
supply
m
e
s
e
The rotor speed or motor speed is :
) 1 ( S
s m
=e e
Where S is slip, as defined as :
S
m S
S
e
e e
=
Or
S
m S
N
N N
S
=
The motor speed
Equivalent Circuit Of Induction Motor
Stator
Three-phase
windings
Rotor
Air gap
e T
Rotor windings
Three-
phase
supply
m
e
s
e
Stator Air gap motor
Vs
Is
Im Ir
Xs
Xr Rs
Rm Xm
Rr/s
Where :
Rs is resistance per-phase of stator winding
Rr is resistance per-phase of rotor winding
Xs is leakage reactance per-phase of the
winding stator
Xs is leakage reactance per-phase of the
winding rotor
X
m
is magnetizing reactance
R
m is
Core losses as a reactance
Performance Characteristic of
Induction Motor
Stator copper loss :
Stator Air gap motor
Vs
Is
Im Ir
Xs
Xr Rs
Rm Xm
Rr/s
s s cu s
R I P
2
3 =
'
2
'
) ( 3
r r cu r
R I P = Rotor copper loss :
m
s
m
m
c
R
V
R
V
P
2 2
3 3 ~ =
Core losses :
S
R
I P
r
r g
'
2
'
) ( 3 =
) 1 ( ) ( 3
'
2
'
S
S
R
I P P P
r
r cu r g d
= =
) 1 ( S P P
g d
=
- Power developed on air gap (Power fropm stator to
rotor through air gap) :
Performance Characteristic of
Induction Motor
- Power developed by motor :
or
- Torque of motor :
m
d
d
P
T
e
=
s
g
S
g
P
S
S P
e e
=
=
) 1 (
) 1 (
or
m
d
d
N
P
T
t 2
60
=
or
m s s i
I V P | cos 3 =
g cu s c
P P P + + =
Input power of motor :
Performance Characteristic of
Induction Motor
load no d o
P P P =
g cu s c
load no d
i
o
P P P
P P
P
P
+ +
= = q
Output power of motor :
Efficiency :
) (
cu s c g
P P P + >>
load no d
P P >>
S
P
S P
P
P
g
g
g
d
=
= ~ 1
) 1 (
q
If
and
so, the efficiency can calculated as :
Performance Characteristic of
Induction Motor
) (
2 2 2
s s m
X R X + >>
s m
V V ~
Generally, value of reactance magnetization X
m
>> value Rm (core
losses) and also
So, the magnetizing voltage same with the input voltage :
s m
V V ~
s m
V V ~
Therefore, the equivalent circuit is ;
Stator Air gap motor
Vs
Is
Im Ir
Xs
Xr Rs
Rm Xm
Rr/s
Stator Air gap rotor
Vs
Ii
Im Ir
Xs Xr Rs
Rr/s
Pi
Po
Is=Ir
Xm
Performance Characteristic of
Induction Motor
) (
) ( ) (
'
'
'
'
r s m
r
s
r
s m r s m
i
X X X j
S
R
R
S
R
R jX X X X
Z
+ + + +
+ + +
=
Total Impedance of this circuit is :
Performance Characteristic of
Induction Motor
Stator Air gap rotor
Vs
Ii
Im Ir
Xs Xr Rs
Rr/s
Pi
Po
Is=Ir
Xm
The rotor current is :
( )
2
1
2
'
2
'
'
(
(
+ +
|
|
.
|
\
|
+
=
r s
r
s
s
r
X X
S
R
R
V
I
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s s
s r
d
X X
S
R
R S
V R
T
e
Stator Air gap rotor
Vs
Ii
Im Ir
Xs Xr Rs
Rr/s
Pi
Po
Is=Ir
Tmax
Smax
Tst
Td
S=0
es
Ns
S=1
TL
S=Sm
em
Nm
Nm =0
Tm=TL
Operating point
Torque speed Characteristic
Tmax
Smax
Tst
S=0
es
Ns
S=1
S=Sm
Nm =0
es es =0
2es
-Tmax
-Smax
S=-1
S=2
Forward
regeneration
Forward
motoring
Reverse
plugging
es
em
es
em
es
em
Torque
Three region operation :
1. Motoring :
2. Regenerating :
3. Plugging :
1 0 s s S
0 < S
2 1 s s S
Starting speed of motor is em = 0 or S = 1,
Performance Characteristic of
Induction Motor
Starting torque of motor is :
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s s
s r
st
X X
S
R
R
V R
T
e
Slip for the maximum torque S
max
can be found by setting :
0 =
dS
T d
d
So, the slip on maximum torque is :
( ) ( ) | |
2
1
2
'
2
'
max
r s s
r
X X R
R
S
+ +
=
( )
(
+ + +
=
2 '
2
2
max
2
3
r s s s s
s
X X R R
V
T
e
Performance Characteristic of
Induction Motor
Torque maximum is :
And the maximum regenerative torque can be found as :
( )
(
+ + +
=
2 '
2
2
max
2
3
r s s s s
s
X X R R
V
T
e
Where the slip of motor s = - S
m
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s s
s r
d
X X
S
R
R S
V R
T
e
Speed-Torque Characteristic :
( )
2
'
2
'
|
|
.
|
\
|
+ >> +
S
R
R X X
r
s r s
( )
2
'
2 '
3
r s s
s r
d
X X S
V R
T
+
=
e
( )
2
'
2 '
3
r s s
s r
st
X X
V R
T
+
=
e
For the high Slip S. (starting)
So, the torque of motor is :
And starting torque (slip S=1) is :
( )
s
r
r s
R
S
R
X X >> << +
' 2
'
r s
s
d
R
S V
T
'
3
2
e
=
For low slip S region, the motor speed near unity or synchronous
speed, in this region the impedance motor is :
So, the motor torque is :
( ) ( ) | |
2
1
2
'
2
'
max
r s s
r
X X R
R
S
+ +
=
And the slip at maximum torque is :
The maximum motor torque is :
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s s
s r
d
X X
S
R
R S
V R
T
e
Tmax
S=0
es
Ns
S=1
TL
Nm =0
Td
Vs1 Vs
Vs2 >
>
e
e1 e2
Tst
Tst1
Tst2
Stator Voltage Control
Controlling Induction Motor Speed by
Adjusting The Stator Voltage
e
Td
IM
AC
Variable
Voltage
Sources
Vs
Stator
air
gap
rotor
Ii
Im Ir
Xs Xr Rs
Rr/s
Pi
Po
Is=Ir
Vs
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s s
s r
d
X X
S
R
R S
V R
T
e
Frequency Voltage Control
Controlling Induction Motor Speed by
Adjusting The Frequency Stator Voltage e Td
IM
AC
Variable
Voltage
Sources
Vs
f
Stator
Air
gap
rotor
I
i
I
m Ir
X
s X
r
R
s
Rr/s
P
i
Po
I
s=Ir
Vs
f
T
max
S=0
S=1
T
L
m =0
T
d
< <
e
1 e
2
T
st
T
st1
T
st2
es
fs
S=0
fs1
fs2
S=0
fs2
fs fs1
e
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s s
s r
d
X X
S
R
R S
V R
T
e
If the frequency is increased above its rated value, the flux and torque
would decrease. If the synchronous speed corresponding to the rated
frequency is call the base speed e
b,
the synchronous speed at any other
frequency becomes:
b s
e | e =
And :
b
m
b
m b
S
|e
e
|e
e |e
=
= 1
The motor torque :
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s s
s r
d
X X
S
R
R S
V R
T
e
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s b
s r
d
X X
S
R
R S
V R
T
| | |e
If R
s
is negligible, the maximum torque at the base speed as :
( )
'
2
2
3
r s b
s
mb
X X S
V
T
+
=
e
And the maximum torque at any other frequency is :
( )
2
2
'
2
3
| e
s
r s b
m
V
X X S
T
+
=
At this maximum torque, slip S is :
( )
'
'
r s
r
m
X X
R
S
+
=
|
Normalizing :
( )
'
2
2
3
r s b
s
mb
X X S
V
T
+
=
e
( )
2
2
'
2
3
| e
s
r s b
m
V
X X S
T
+
=
2
1
|
=
mb
m
T
T
And
mb m
T T =
2
|
Example :
A three-phase , 11.2 kW, 1750 rpm, 460 V, 60 Hz, four pole, Y-connected
induction motor has the following parameters : Rs = 0.1O, Rr = 0.38O, Xs =
1.14O, Xr = 1.71O, and Xm = 33.2O. If the breakdown torque requiretment is
35 Nm, Calculate : a) the frequency of supply voltage, b) speed of motor at
the maximum torque
Solution :
Input voltage per-phase : volt V
s
265
3
460
= =
s rad x x f
b
/ 377 60 14 . 3 2 2 = = = t e Base frequency :
Nm
x x
x
N
P
T
m
o
mb
11 . 61
1750 14 . 3 2
11200 60
2
60
= = =
t
Nm T
m
35 =
Base Torque :
Motor Torque :
a) the frequency of supply voltage :
2
1
|
=
mb
m
T
T
321 . 1
35
11 . 61
= = =
m
mb
T
T
|
Synchronous speed at this frequency is :
b s
e | e =
s rad x
s
/ 01 . 498 377 321 . 1 = = e
or
rpm
x
x
N N
b s
65 . 4755
2
01 . 498 60
= = =
t
|
So, the supply frequency is :
Hz
x N p
f
b
S
s
52 . 158
120
65 . 4755 4
120
= = =
b) speed of motor at the maximum torque :
At this maximum torque, slip S
m
is :
( )
'
'
r s
r
m
X X
R
S
+
=
|
Rr = 0.38O, Xs = 1.14O, Xr = 1.71O and | = 1.321
( )
101 . 0
71 . 1 14 . 1 321 . 1
38 . 0
=
+
=
m
S
So,
rpm S N N
S m
4275 ) 101 . 0 1 ( 65 . 4755 ) 1 ( = = =
or,
CONTROLLING INDUCTION MOTOR SPEED USING
ROTOR RESISTANCE
(Rotor Voltage Control)
Wound rotor induction motor applications
cranes
CONTROLLING INDUCTION MOTOR SPEED USING
ROTOR RESISTANCE
(Rotor Voltage Control)
Equation of Speed-Torque :
( )
(
(
+ +
|
|
.
|
\
|
+
=
2
'
2
'
2 '
3
r s
r
s s
s r
d
X X
S
R
R S
V R
T
e
r s
s
d
R
S V
T
'
3
2
e
=
In a wound rotor induction motor, an external
three-phase resistor may be connected to its
slip rings,
Three-phase
supply
Rotor
Stator
RX
RX
RX
These resistors Rx are used to control motor starting and stopping
anywhere from reduced voltage motors of low horsepower up to
large motor applications such as materials handling, mine hoists,
cranes etc.
The most common applications are:
AC Wound Rotor Induction Motors where the resistor is wired into the
motor secondary slip rings and provides a soft start as resistance is
removed in steps.
AC Squirrel Cage Motors where the resistor is used as a ballast for soft
starting also known as reduced voltage starting.
DC Series Wound Motors where the current limiting resistor is wired to
the field to control motor current, since torque is directly proportional to
current, for starting and stopping.
The developed torque may be varying the resistance Rx
The torque-speed characteristic for variations in rotor resistance
This method increase the starting torque while limiting the starting current.
The wound rotor induction motor are widely used in applications requiring
frequent starting and braking with large motor torque (crane, hoists, etc)
The three-phase resistor may be replaced by a three-phase diode rectifier
and a DC chopper. The inductor Ld acts as a current source Id and the DC
chopper varies the effective resistance:
) 1 ( k R R
e
=
Where k is duty cycle of DC chopper
The speed can controlled by varying the duty cycle k, (slip power)
Three-phase
supply
Rotor
Stator
D1
D2
D3
D6 D4
D5
GTO
R Vdc
Id
Ld
Vd
The slip power in the rotor circuit may be returned to the supply by
replacing the DC converter and resistance R with a three-phase full
converter (inverter)
Three-phase
supply
Rotor
Stator
D1
D2
D3
D6 D4
D5
Id
Ld
Vd
T2
T5
T4
T3 T1
T6
Vdc
Transformer
Na:Nb
Diode rectifier
Controlled rectifier/
inverter
Slip Power
Example:
A three-phase induction motor, 460, 60Hz, six-pole, Y connected, wound rotor
that speed is controlled by slip power such as shown in Figure below. The
motor parameters are Rs=0.041 O, Rr=0.044 O, Xs=0.29 O, Xr=0.44 O and
Xm=6.1 O. The turn ratio of the rotor to stator winding is nm=Nr/Ns=0.9. The
inductance Ld is very large and its current Id has negligible ripple.
The value of Rs, Rr, Xs and Xr for equivalent circuit can be considered
negligible compared with the effective impedance of Ld. The no-load of motor is
negligible. The losses of rectifier and Dc chopper are also negligible.
The load torque, which is proportional to speed square is 750 Nm at 1175 rpm.
(a) If the motor has to operate with a minimum speed of 800 rpm, determine
the resistance R, if the desired speed is 1050 rpm,
(b) Calculate the inductor current Id.
(c) The duty cycle k of the DC chopper.
(d) The voltage Vd.
(e) The efficiency.
(f) The power factor of input line of the motor.
volt V
s
58 . 265
3
460
= =
6 = p
s rad x / 377 60 2 = = t e
s rad x
s
/ 66 . 125 6 / 377 2 = = e
The equivalent circuit :
The dc voltage at the rectifier output is :
) 1 ( k R I R I V
d e d d
= =
m s
s
r
s r
n V S
N
N
V S E = =
and
For a three-phase rectifier, relates Er and Vd as :
r r d
E E x V 3394 . 2 2 65 . 1 = =
Using :
m s
s
r
s r
n V S
N
N
V S E = =
m s d
n V S V 3394 . 2 =
If Pr is the slip power, air gap power is :
S
P
P
r
g
=
Developed power is :
S
S P
S
S
P
P P P
r r
r g d
) 1 ( 3
) ( 3 ) ( 3
= = =
Because the total slip power is 3Pr = Vd Id and
m L d
T P e =
So,
) 1 (
) 1 (
S T T
S
I V S
P
m L m L
d d
d
= =
= e e
Substituting Vd from
m s d
n V S V 3394 . 2 =
In equation Pd above, so
:
Solving for Id gives :
m s
s L
d
n V
T
I
3394 . 2
e
=
Which indicates that the inductor current is independent of the speed.
From equation :
) 1 ( k R I R I V
d e d d
= =
and equation :
m s d
n V S V 3394 . 2 =
So,
m s d
n V S k R I 3394 . 2 ) 1 ( =
Which gives :
m s
d
n V S
k R I
S
3394 . 2
) 1 (
=
The speed can be found from equation :
m s
d
n V S
k R I
S
3394 . 2
) 1 (
=
as :
(
= =
m s
d
s s m
n V
k R I
S
3394 . 2
) 1 (
1 ) 1 ( e e e
(
=
2
) 3394 . 2 (
) 1 (
1
m s
s L
s m
n V
k R T e
e e
Which shows that for a fixed duty cycle, the speed decrease with load
torque. By varying k from 0 to 1, the speed can be varied from minimum
value to es
s rad
m
/ 77 . 83 30 / 180 = = t e
From torque equation :
2
m v L
K T e =
Nm x 67 . 347
1175
800
750
2
=
|
.
|
\
|
=
From equation :
m s
s L
d
n V
T
I
3394 . 2
e
= The corresponding inductor current is :
A
x x
x
I
d
13 . 78
9 . 0 58 . 265 3394 . 2
66 . 125 67 . 347
= =
The speed is minimum when the duty-cycle k is zero and equation :
(
= =
m s
d
s s m
n V
k R I
S
3394 . 2
) 1 (
1 ) 1 ( e e e
)
9 . 0 58 . 265 3394 . 2
13 . 78
1 ( 66 . 125 77 . 83
x x
R
=
And : O = 3856 . 2 R
Vous aimerez peut-être aussi
- Advanced Electric Drives: Analysis, Control, and Modeling Using MATLAB / SimulinkD'EverandAdvanced Electric Drives: Analysis, Control, and Modeling Using MATLAB / SimulinkPas encore d'évaluation
- Which Is Defined By:: Synchronous SpeedDocument15 pagesWhich Is Defined By:: Synchronous SpeedYudhy SufbrataPas encore d'évaluation
- Kramer DriveDocument42 pagesKramer DriveSenthil Kumar100% (1)
- Chap 7 Solutions PDFDocument34 pagesChap 7 Solutions PDFIbrahim Hussain100% (1)
- Solid State Drives: Notes of Lesson PlanDocument24 pagesSolid State Drives: Notes of Lesson PlanetasureshPas encore d'évaluation
- Induction Motor Modeling - Steady StateDocument43 pagesInduction Motor Modeling - Steady Statedivinelight100% (3)
- Induction Machines: Torque Speed CharacteristicsDocument22 pagesInduction Machines: Torque Speed CharacteristicsGogioman Myhay100% (1)
- Induction MotorDocument65 pagesInduction MotorAhmad Nawawi Ngah100% (1)
- Experiments EMS IIDocument117 pagesExperiments EMS IIOsama Tahir100% (1)
- 7 Asynchronous StudentDocument33 pages7 Asynchronous Studentwanted_JMTIPas encore d'évaluation
- ELEC 2032 (3) Electromechanical System: Induction Motor IIIDocument19 pagesELEC 2032 (3) Electromechanical System: Induction Motor IIIAshvin AshPas encore d'évaluation
- Induction MotorDocument39 pagesInduction MotorAhmed MagdyPas encore d'évaluation
- Introduction: The Induction Motor Is A Three Phase AC Motor and Is The Most WidelyDocument13 pagesIntroduction: The Induction Motor Is A Three Phase AC Motor and Is The Most WidelyAsimPas encore d'évaluation
- Induction Machines: Steady State Torque Speed CharacteristicDocument9 pagesInduction Machines: Steady State Torque Speed CharacteristicRyan Benjamin100% (1)
- Machine Reviewer 2Document4 pagesMachine Reviewer 2Jimmy OrajayPas encore d'évaluation
- #2Document18 pages#2tsegaye2321Pas encore d'évaluation
- The Rotor Speed or Motor Speed IsDocument4 pagesThe Rotor Speed or Motor Speed Issm7279Pas encore d'évaluation
- Induction Motor Speed ControlDocument46 pagesInduction Motor Speed Controlsolo400060% (10)
- InductionMotors Gate Material PartBDocument38 pagesInductionMotors Gate Material PartBpraveen6494Pas encore d'évaluation
- Speed Control of DC Motors (DC Drives)Document27 pagesSpeed Control of DC Motors (DC Drives)gopi_905Pas encore d'évaluation
- Ied Unit VDocument8 pagesIed Unit VRudra Kumar MishraPas encore d'évaluation
- Induction MachineDocument48 pagesInduction MachinechethanPas encore d'évaluation
- Assignment EE 4202Document10 pagesAssignment EE 4202Chanki P PyrbotPas encore d'évaluation
- Solid State Drives Short BookDocument25 pagesSolid State Drives Short BookGomathi Raja MPas encore d'évaluation
- Final Exam SEE3433 Mei (Solution)Document9 pagesFinal Exam SEE3433 Mei (Solution)Fizah Abdul RahmanPas encore d'évaluation
- Induction Machines: Principle of Operation and Equivalent Circuit ModelDocument15 pagesInduction Machines: Principle of Operation and Equivalent Circuit ModelRyan BenjaminPas encore d'évaluation
- Exp 8Document7 pagesExp 8Tejas MayekarPas encore d'évaluation
- Electrical Machines Technology II-EMT226C-Three Phase Induction Motors-New NotesDocument63 pagesElectrical Machines Technology II-EMT226C-Three Phase Induction Motors-New NotesTinyiko ChaukePas encore d'évaluation
- Induction Machines - Asynchronous MachinesDocument43 pagesInduction Machines - Asynchronous MachinesMustafa ÖzdemirPas encore d'évaluation
- EE462 Lab Assignement 1Document14 pagesEE462 Lab Assignement 1Terry rickyPas encore d'évaluation
- Induction MotorDocument39 pagesInduction MotorSaneer M SaliPas encore d'évaluation
- Induction Motors: The Concept of Rotor SlipDocument12 pagesInduction Motors: The Concept of Rotor Sliphafiz_jaaffarPas encore d'évaluation
- All ExpDocument37 pagesAll ExpMuhammad SameerPas encore d'évaluation
- Test 2 2013 SolutionDocument6 pagesTest 2 2013 SolutionFizah Abdul RahmanPas encore d'évaluation
- Servo MotorDocument15 pagesServo MotorMinh HảiPas encore d'évaluation
- Torque Sensors: Common Sensing MethodsDocument32 pagesTorque Sensors: Common Sensing MethodsvishiwizardPas encore d'évaluation
- Speed Control of 3 Phase Induction Motor 1 Aim: Experiment No: 3Document10 pagesSpeed Control of 3 Phase Induction Motor 1 Aim: Experiment No: 3rohitkjPas encore d'évaluation
- Caculate Rotary LinearDocument3 pagesCaculate Rotary LinearTrinh Luong MienPas encore d'évaluation
- Induction MotorDocument41 pagesInduction MotorRiyadh Al Nur0% (1)
- MECHDocument36 pagesMECHPalak AriwalaPas encore d'évaluation
- DC MotorDocument17 pagesDC MotorBijoy AyyagariPas encore d'évaluation
- Acdrives AssignDocument5 pagesAcdrives AssignRaja DesinguPas encore d'évaluation
- DC Servo MotorDocument6 pagesDC Servo MotortaindiPas encore d'évaluation
- FlywheelsDocument33 pagesFlywheelsKaranSinghPas encore d'évaluation
- Hydraulics and Water Resources (CEE 340) (Topic 2) : TurbineDocument12 pagesHydraulics and Water Resources (CEE 340) (Topic 2) : TurbineRachel YarasavichPas encore d'évaluation
- ECE 8830 - Electric Drives: Topic 11: Slip-Recovery Drives For Wound-Field Induction MotorsDocument42 pagesECE 8830 - Electric Drives: Topic 11: Slip-Recovery Drives For Wound-Field Induction MotorsVikas Roy100% (1)
- ECE330 HW6 SolutionDocument4 pagesECE330 HW6 SolutionHuynh BachPas encore d'évaluation
- Induction MotorsDocument14 pagesInduction MotorsAbdul RaheemPas encore d'évaluation
- Exp. 3 - Load Test and Equivalent Circuit Determination On Three Phase Squirrel Cage Induction Motor andDocument9 pagesExp. 3 - Load Test and Equivalent Circuit Determination On Three Phase Squirrel Cage Induction Motor andSanjay MeenaPas encore d'évaluation
- AC Drives: Dr. Adel A. El-Samahy Department of Electrical Engineering University of HelwanDocument25 pagesAC Drives: Dr. Adel A. El-Samahy Department of Electrical Engineering University of Helwanadelelsamahy5958Pas encore d'évaluation
- Turning Moment Diagram1Document25 pagesTurning Moment Diagram1Bibin BabyPas encore d'évaluation
- Elx 311 Chap 7 SlidesDocument23 pagesElx 311 Chap 7 SlidesDaniyar SeytenovPas encore d'évaluation
- G.H. Raisoni College of EngineeringDocument34 pagesG.H. Raisoni College of Engineeringnikhil_0401Pas encore d'évaluation
- Help - Asynchronous Machine - Blocks (SimPowerSystems™) PDFDocument23 pagesHelp - Asynchronous Machine - Blocks (SimPowerSystems™) PDFnmulyonoPas encore d'évaluation
- Et Cs PDFDocument33 pagesEt Cs PDFsahil borichaPas encore d'évaluation
- 110 Waveform Generator Projects for the Home ConstructorD'Everand110 Waveform Generator Projects for the Home ConstructorÉvaluation : 4 sur 5 étoiles4/5 (1)
- Variable Speed AC Drives with Inverter Output FiltersD'EverandVariable Speed AC Drives with Inverter Output FiltersPas encore d'évaluation
- Reference Guide To Useful Electronic Circuits And Circuit Design Techniques - Part 2D'EverandReference Guide To Useful Electronic Circuits And Circuit Design Techniques - Part 2Pas encore d'évaluation
- Speed Control of DC Motors (DC Drives)Document27 pagesSpeed Control of DC Motors (DC Drives)gopi_905Pas encore d'évaluation
- DC MachineDocument30 pagesDC Machineattaullahjohar040Pas encore d'évaluation
- ResearchDocument113 pagesResearchSeshagirirao GalamPas encore d'évaluation
- Transistor Inverter Inverter For Air Conditioner IGBT Gate Drive Power MOS FET Gate DriveDocument7 pagesTransistor Inverter Inverter For Air Conditioner IGBT Gate Drive Power MOS FET Gate DriveSeshagirirao GalamPas encore d'évaluation