GROUPE SCOLAIRE MARIE ALBERT ANNÉE SCOLAIRE 2023-2024

NIVEAU : Tle C

DEPARTEMENT DE MATHEMATIQUES CHRONO N°2

THÈME 1 : ARITHMÉTIQUE
Exercice 1 :
1- Énoncé et démontrer le théorème de GAUSS.
𝑝𝑔𝑐𝑑(𝑎; 𝑏) = 1
2- Déterminer deux entiers naturels 𝑎 et 𝑏 tels que { 𝑎+21 𝑎
=𝑏
𝑏+15
𝑛 ≡ 1[5]
3- Résoudre dans ℕ le système suivant : {𝑛 ≡ 5[7]
𝑛∈ℕ
Exercice 2 :
On considère l’équation (𝐸): 𝑛2 − 7𝑛 + 77 ≡ 0[107]; où 𝑛 ∈ ℤ.
1) Démontrer que 107 est un nombre premier.
2) Soient 𝐴 et 𝑏 deux nombres entiers relatifs donnés.
Démontrer que 𝑎𝑏 ≡ 0[107] ⟺ (𝑎 ≡ 0[107] 𝑜𝑢 𝑏 ≡ 0[107]).
3) Démontrer que pour tout entier relatif 𝑛, on a : 𝑛2 − 7𝑛 + 77 ≡ (𝑛 + 3)(𝑛 − 10)[107].
4) Résoudre alors l’équation (𝐸) dans ℤ.

Exercice 3 :
𝑎 est un nombre entier naturel non nul. On pose 𝐴 = 211 ̅̅̅̅̅ 𝑎 ; 𝐵 = 312
̅̅̅̅̅ 𝑎 et 𝐶 = 133032
̅̅̅̅̅̅̅̅̅̅ 𝑎
1 . Montrer que 𝑎 ≥ 4.
2. On suppose que 𝐶 = 𝐴 × 𝐵.
a) montrer que 𝑎3 − 3𝑎2 − 2𝑎 − 8 = 0.
b) En déduire que 𝑎 divise 8 puis en déduire alors 𝑎.
3. On suppose que 𝑎 = 4.
a) Écrire 𝐴, 𝐵 et 𝐶 dans le système décimal.
b) Montrer alors que 𝐴 × 𝐵 = 𝑃𝑃𝐶𝑀(𝐴, 𝐵) .
Exercice 4 :
1. Déterminer deux entiers relatifs 𝑢 et 𝑣 tels que 3𝑢 + 5𝑢 = 1.
2. On considère dans le plan rapporté à un repère orthonormal la droite (𝐷) d’équation
3𝑥 + 5𝑦 − 1 = 0. Déterminer un point du plan à coordonnées entières appartenant à (𝐷)
3. On cherche à déterminer tous les points du plan à coordonnées entières appartenant à (𝐷).
Soit 𝑀 (𝑥 ; 𝑦) un point à coordonnées entières appartenant à (𝐷).
a) Démontrer que 3(𝑥 − 𝑢) = 5(𝑣 − 𝑦). (𝑢 et 𝑣 étant les entiers trouvés dans la 1è𝑟𝑒 question)
b) En déduire qu’il existe un entier relatif 𝑘 tels que : 𝑥 − 𝑢 = 5𝑘 et 𝑦 − 𝑣 = −3𝑘.
c) Justifier que l’ensemble des points à coordonnées entières de (𝐷) est l’ensemble des points de coordonnées (𝑢 + 5𝑘 ; 𝑣 − 3𝑘)
avec 𝑘 ∈ ℤ.
4. Déterminer tous les points à coordonnées entières de (𝐷) appartenant aussi au disque de centre 𝑂 (0 ; 0) et de rayon 𝑅 = 10.
Exercice 5 :
7
Dans le plan muni d’un repère orthonormé (𝑂, 𝑖⃗, 𝑗⃗), on considère les points A(12 ), 𝐵(70) et 𝐶(12
0
).
1. a) Vérifier que la droite (𝑂𝐴) a pour équation :12𝑥 − 7𝑦 = 0.
b. En déduire les points de coordonnées entières qui appartiennent à la droite (𝑂𝐴).
c. En déduire les points de coordonnées entières qui appartiennent au segment [𝑂𝐴].
2. Résoudre dans ℤ × ℤ les équations 12𝑥 − 7𝑦 = 1 et 12𝑥 − 7𝑦 = − 1.
3. Soit 𝑀 (𝑥𝑦 ) un point du plan à coordonnées entières tel que 𝑀 soit à l’intérieur du rectangle 𝐴𝐵𝑂𝐶.
|12𝑥−7𝑦|
a) Montrer que la distance du point 𝑀 à la droite (𝑂𝐴) est .
√193
b. En déduire qu’à l’intérieur du rectangle 𝐴𝐵𝑂𝐶, il existe deux points 𝐼 et 𝐽 de coordonnées
entières et tels que la distance de chacun d’entre eux à la droite (𝑂𝐴) soit minimale.
4. Vérifier que le quadrilatère 𝑂𝐼𝐴𝐽 est un parallélogramme et calculer son aire.

Exercice 6 :
Dans tout l’exercice, on pose On pose 𝑇𝑛 = 13 + 23 + ⋯ + 𝑛3 , 𝑛 ∈ ℕ∗ et on supposera que si 𝑃𝐺𝐶𝐷(𝑎; 𝑏) =
1 alors 𝑃𝐺𝐶𝐷(𝑎2 ; 𝑏 2 ) = 1.
𝑛(𝑛+1) 2
1- Démontrer par récurrence que Tn = [ 2 ] .
2- On suppose que 𝑛 = 2𝑘 + 1, 𝑘 ∈ ℕ∗ .
Démontrer que 𝑃𝐺𝐶𝐷(2𝑘 + 1; 2𝑘 + 3) = 1, puis en déduire 𝑃𝐺𝐶𝐷(Tn ; Tn+1 ).

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 1/12

3- On suppose que 𝑛 = 2𝑘.
a- Démontrer que 𝑃𝐺𝐶𝐷(𝑇𝑛 ; 𝑇𝑛+1 ) = (2𝑘 + 1)2 𝑃𝐺𝐶𝐷(𝑘 2 ; (𝑘 + 1)2 ) , puis Calculer 𝑃𝐺𝐶𝐷(𝑘; 𝑘 + 1).
b-En déduire 𝑃𝐺𝐶𝐷(𝑇𝑛 ; 𝑇𝑛+1 ).
4- Déduire des questions précédentes qu’il existe une unique valeur de 𝑛 à déterminer, pour laquelle 𝑇𝑛 et 𝑇𝑛+1 sont
premiers entre eux.

THÈME 2 : FONCTIONS NUMÉRIQUES ET SUITES

Exercice 1 :
9+𝑥 2
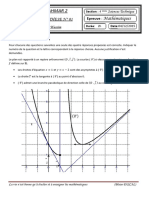
Soit la fonction 𝑓 définie sur [0; +∞[ par 𝑓(𝑥) = 2𝑥 et dont la courbe représentative est donnée sur la feuille
annexe.
𝑢0 = 6
Soit (𝑢𝑛 ) la suite définie sur ℕ par :{ 9+𝑢2 , ∀ 𝑛 ∈ ℕ.
𝑢𝑛+1 = 2𝑢 𝑛
𝑛
1) Faire une représentation en chemin des quatre premiers termes de la suite (𝑢𝑛 )𝑛∈ℕ
(On laissera paraître toutes les traces liées à la construction).
2) Montrer que pour tout 𝑛 ∈ ℕ, 𝑢𝑛 > 3.
3- a) Montrer que (𝑢𝑛 ) est une suite décroissante.
b) En déduire que la suite (𝑢𝑛 ) est convergente et déterminer sa limite.
1
4- a) Montrer que pour tout ∈ ℕ, 𝑢𝑛+1 − 3 ≤ 2 (𝑢𝑛 − 3).
1 𝑛
b) En déduire que pour tout ∈ ℕ, 0 < 𝑢𝑛 − 3 ≤ 3 × (2) .
c) Retrouver alors le résultat de la question 3.b).
3n−4
5) On définit la suite (wn ) par : ∀ n ∈ ℕ, wn = 2n+1 .
3
Démontrer en utilisant la définition formelle (définition avec 𝜀) que lim 𝑤𝑛 = 2.
𝑛→+∞

Exercice 2 :
√1−𝑥 2
I- On considère la fonction 𝑓 définie sur [−1; 1] ∖ {0} par 𝑓(𝑥) = 1 + . On note (𝐶) sa courbe représentative
𝑥
dans un repère orthonormé.
1- Calculer lim+ 𝑓(𝑥) ; lim− 𝑓(𝑥) et interpréter les résultats obtenus.
𝑛→0 𝑛→0
2-a) Étudier la dérivabilité de 𝑓 au point d(abscisse 𝑥 = −1 et interpréter le résultat obtenu.
b) Étudier la dérivabilité de 𝑓 au point d(abscisse 𝑥 = 1 et interpréter le résultat obtenu.
−1
2-a) Montrer que : ∀𝑥 ∈ ]−1,1[ ∖ {0} ∶ 𝑓 ′ (𝑥) = 2 2
.
𝑥 √1−𝑥
b) Dresser le tableau de variation de la fonction 𝑓.
c) Montrer que 𝑓 réalise une bijection de ]0,1[ sur un intervalle 𝐽 à préciser .
c) Expliciter 𝑓 −1 (𝑥) pour tout 𝑥 de 𝐽 .
3) Représenter dans le même repère la courbe (𝐶) et la courbe (𝐶′) de 𝑓 −1 .
𝜋
II- On considère maintenant la fonction 𝑔 définie sur [0, 2 [ par 𝑔(𝑥) = 𝑓(𝑐𝑜𝑠𝑥).
𝜋
1- Montrer que pour tout 𝑥 de [0, 2 [, 𝑔(𝑥) = 1 + 𝑡𝑎𝑛(𝑥).
2- Étudier le sens de variation de la fonction 𝑔.
𝜋 𝜋
3- Montrer que l’équation 𝑔(𝑥) = 𝑥 admet une unique solution 𝜃 dans [0, 2 [ et vérifier que 0 < 𝜃 < 4 .
𝜋
b) Montrer que 𝑔réalise une bijection de [0, 2 [ sur un intervalle 𝐾 à préciser .
1
c) Montrer que 𝑔−1 est dérivable sur 𝐾 et que pour tout 𝑥 de 𝐾, (𝑔−1 )′ (𝑥) = 𝑥 2−2𝑥+2 .

1
III- Soit la fonction ℎ définie sur ℝ ∖ {−1} par : ℎ(𝑥) = . Montrer par récurrence que pour tout
𝑥+1
(−1)𝑛 ×𝑛!
entier naturel 𝑛 non nul, (ℎ)(𝑛) (𝑥) = (𝑥+1)𝑛+1 , où (ℎ)(𝑛) désigne la fonction dérivée 𝑛 − 𝑖è𝑚𝑒 de la fonction ℎ.

Exercice 3 :
1
Soit 𝑔 la fonction définie sur 𝐽 = [2 ; 1] par : 𝑔(𝑥) = 𝑐𝑜𝑠𝑥.
1- Montrer que l’équation 𝑔(𝑥) = 𝑥 admet une unique solution 𝛽 dans l’intervalle 𝐽.
1- Montrer que pour tout 𝑥 ∈ 𝐽 on a :
9
a) |𝑔′(𝑥)| ≤ . b) 𝑔(𝐽) ⊂ 𝐽.
10
2- On définit la suite (𝑢𝑛 )𝑛∈ℕ par : 𝑢0 = 0 et 𝑢𝑛+1 = 𝑐𝑜𝑠𝑢𝑛
1
a) Montrer que pour tout entier naturel 𝑛, non nul, 2 ≤ 𝑢𝑛 ≤ 1.
9
b) En déduire que : |𝑢𝑛+1 − 𝛽| ≤ 10 |𝑢𝑛 − 𝛽|.

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 2/12

 1 9 𝑛
3- a) Montrer par récurrence que pour tout entier naturel 𝑛, on a: |𝑢𝑛 − 𝛽| ≤ 2 (10) .
b) En déduire que la suite (𝑢𝑛 )𝑛∈ℕ converge et déterminer sa limite.

Exercice 4 :
2𝑥
Soit la fonction 𝑓 définie sur par ℝ : 𝑓(𝑥) = 1 + 2
. On désigne par sa (𝒞) courbe représentative dans
√𝑥 +1
le plan muni d ' un repère orthonormé(𝑂, 𝑖⃗, 𝑗⃗).
1. a) Montrer que lim 𝑓(𝑥) = 1 et lim 𝑓(𝑥) = 3. Interpréter graphiquement ces résultats.
𝑥→−∞ 𝑥→+∞
2
2 b) Montrer que 𝑓 est dérivable sur ℝ et ∀𝑥 ∈ ℝ ; 𝑓 ′(𝑥) = .
(𝑥 2+1)√𝑥 2+1
c) Dresser le tableau de variation de 𝑓.
d) Vérifier que 𝑓([2,3]) ⊂ [2,3].
2
e) Montrer que pour tout 𝑥 ∈ [2,3] ; 𝑓 ′(𝑥) ≤ 5√5 .
2. a) Montrer que l'équation 𝑓(𝑥) = 𝑥 admet une seule solution 𝛼 dans l'intervalle]2,3[ et donner un
encadrement de 𝛼 à 10−2 près.
b) Donner une équation de la tangente 𝒯 à la courbe (𝒞) au point d'abscisse 0.
c) Montrer que le point 𝐼(01) est un centre de symétrie pour la courbe (𝒞).
d) Tracer 𝒯 et (𝒞)
3) a) Montrer que 𝑓 réalise une bijection de ℝ sur un intervalle 𝐽 que l'on précisera.
On note 𝑓 −1 sa fonction réciproque.
b) Tracer la courbe représentative (𝒞′) de 𝑓 −1 dans le même repère que (𝒞) .
𝑢0 =2
4) Soit (𝑢 𝑛 ) la suite réelle définie par : { , ∀𝑛 ∈ ℕ.
𝑢 𝑛+1 = 𝑓(𝑢 𝑛 )
a) Montrer que pour tout 𝑛 ∈ ℕ, 2 ≤ 𝑢 𝑛 ≤ 3.
2
b) Montrer que pour tout 𝑛 ∈ ℕ, |𝑢 𝑛+1 − 𝛼| ≤ 5√5 |𝑢 𝑛 − 𝛼|.
2 𝑛
c) Montrer par récurrence que pour tout 𝑛 ∈ ℕ, |𝑢 𝑛 − 𝛼| ≤ (5√5) |2 − 𝛼|.
d) En déduire que (𝑢 𝑛 ) est convergente et préciser sa limite.

THÈME 3 : ESPACES VECTORIELS, APPLICATIONS LINÉAIRES EN DIMENSION 3

ET PRODUIT VECTORIEL

Exercice 1 :
On muni l’espace d’un repère orthonormée directe (𝑂, 𝑖⃗, 𝑗⃗, 𝑘 ⃗⃗ ). On considère les points 𝐴(1,0,1), 𝐵(2,1,0) , 𝐶(0,1, −1) et
𝐷(−1,0,4).
1- a) Calculer ⃗⃗⃗⃗⃗⃗
𝐴𝐵 . ⃗⃗⃗⃗⃗⃗
𝐴𝐶 ; puis en déduire la valeur de 𝑐𝑜𝑠 𝐵𝐴𝐶 ̂.
b) Montrer que l’on peut déduire la mesure de l’angle 𝐵𝐴𝐶 ̂ à partir de la valeur de 𝑐𝑜𝑠 𝐵𝐴𝐶̂ ; puis
déterminer cette mesure.
2- a) Calculer ⃗⃗⃗⃗⃗⃗
𝐴𝐵 ∧ 𝐴𝐶 ⃗⃗⃗⃗⃗⃗ ; puis en déduire la valeur de 𝑠𝑖𝑛 𝐵𝐴𝐶
̂.
b) Montrer que l’on ne peut pas déduire la mesure de l’angle 𝐵𝐴𝐶 ̂ à partir de la valeur de 𝑠𝑖𝑛 𝐵𝐴𝐶̂.
3- a) Montrer que les points 𝐴, 𝐵, 𝐶 et 𝐷 ne sont pas coplanaires.
b) En déduire le volume du tétraèdre 𝐴𝐵𝐶𝐷.
4- Soit (∆) la droite passant par 𝐷 et dirigée par le vecteur 𝑢⃗⃗(2,2,4).
a) Montrer que la droite (∆) est perpendiculaire au plan (𝐴𝐵𝐶).
b) Déterminer une représentation paramétrique de la droite (∆).
c) Déterminer une équation cartésienne du plan (𝐴𝐵𝐶).
d) En déduire les coordonnées du projété orthogonal du point 𝐷 sur le plan (𝐴𝐵𝐶).
5- Calculer de deux manières la distance du point 𝐷 au plan (𝐴𝐵𝐶).

Exercice 2 :
Soit 𝐸 un espace vectoriel rapporté à une base B = (𝑖⃗ ; 𝑗⃗ ; 𝑘 ⃗⃗ ). Soient 𝑎⃗ et 𝑛⃗⃗ deux vecteurs de 𝐸 tels que : 𝑎⃗ = 𝑖⃗ − 𝑗⃗ + 𝑘
⃗⃗
⃗⃗ ⃗⃗
et 𝑛⃗⃗ = 𝑖⃗ + 𝑗⃗ + 𝑘 . À tout vecteur 𝑢⃗⃗ = 𝑥𝑖⃗ + 𝑦𝑗⃗ + 𝑧𝑘 de 𝐸, on associe l’application 𝑓 définie de 𝐸 dans lui-même par :
𝑓(𝑢⃗⃗) = (𝑎⃗ ⋀ 𝑢 ⃗⃗) ⋀ 𝑛⃗⃗.
1) Démontrer que 𝑓 est un endomorphisme de 𝐸 et déterminer sa matrice 𝑀 dans la base B .
2) Démontrer que 𝑓 est une projection vectorielle.
3) Montrer que 𝐾𝑒𝑟(𝑓) est une droite vectorielle dont on donnera une base 𝑒⃗1 .
4-a) Montrer que 𝐼𝑚(𝑓) est un plan vectoriel 𝑃 de vecteur normal 𝑛⃗⃗. Donner une base (𝑒⃗2 ; 𝑒⃗3 ).
b) Montrer que (𝑒⃗1 ; 𝑒⃗2 ; 𝑒⃗3 ) est une base de 𝐸.
c) Déterminer la matrice de f dans la base (𝑒⃗1 ; 𝑒⃗2 ; 𝑒⃗3 ).

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 3/12

 Exercice 3 :

I- Soit E un espace vectoriel de dimension 3 et 𝔅 = (𝑖⃗, 𝑗⃗, 𝑘 ⃗⃗ ) une base de E. 𝑓 est l’endomorphisme de E défini par 𝑓(𝑖⃗) =
⃗⃗ ⃗⃗
𝑖⃗ + 𝑗⃗; 𝑓(𝑗⃗) = 𝑗⃗ − 𝑘; 𝑓(𝑘) = 𝑖⃗ + 𝑘⃗⃗
1-a) Démontrer (𝑓(𝑖⃗), 𝑓(𝑗⃗), (𝑘 ⃗⃗ )) que est une base de E.
b) En déduire que 𝑓 est un automorphisme de E.
⃗⃗ )).
c) Déterminer la matrice de 𝑓 dans la base (𝑓(𝑖⃗), 𝑓(𝑗⃗), (𝑘
2- Soit 𝑢⃗⃗(𝑥, 𝑦, 𝑧) un vecteur de E.
a) Déterminer les composantes (𝑥 ′ , 𝑦 ′ , 𝑧′)de 𝑓(𝑢
⃗⃗) dans la base 𝔅.
b) Démontrer que 𝐾𝑒𝑟𝑓 est une droite vectorielle dont on donnera une base.
c) Démontrer que 𝑓(𝑢⃗⃗) = (𝑥 + 𝑧)𝑓(𝑖⃗) + (𝑦 − 𝑧)𝑓(𝑗⃗).
d) En déduire que 𝐼𝑚𝑓 est un plan vectoriel dont une base est (𝑓(𝑖⃗), 𝑓(𝑗⃗)).
0 −2 −1
II-On considère la matrice 𝐷 = ( 1 3 1).
−1 −2 0
1- Démontrer que 2𝐷 − 𝐷 2 = 𝐼3 .
2- En déduire que 𝐷 est inversible et déterminer 𝐷 −1 .

Exercice 4 :

⃗⃗ ).
On muni l’espace d’un repère orthonormée directe (𝑂, 𝑖⃗, 𝑗⃗, 𝑘
On considère les points 𝐴(1, −2,1), 𝐵(2, −1,3) , 𝐶(1,1,4) et 𝐷(0,0,2).
𝑥 =𝑡+2
La droite (d) définie par : {𝑦 = 𝑡 + 2 , 𝑡 ∈ ℝ
𝑧 = −𝑡
1- Démontrer que les points A, B et C ne sont pas alignés.
2- Écrire une équation cartésienne du plan (ABC).
3- Démontrer que la droite (d) est perpendiculaire au plan (ABC).
4- Démontrer que H est équidistant de A,B et C.
5- Soit M un point variable de (d) et E(2,2,0) un point fixe de (d).
Déterminer les valeurs de 𝑡 pour que le volume du tétraèdre MABC soit égal au double de celui de EABC..
6- a) Donner une équation cartésienne du plan médiateur du segment [AE ].
b) Donner une équation de la sphère circonscrit au tétraèdre EABC.

THÈME 4 : NOMBRES COMPLEXES, CONIQUES ET SIMILITUDES DIRECTES

Exercice 1 :
1- On donne le polynôme à variable complexe 𝑧 définie par : 𝑔(𝑧) = 3𝑧 3 − 4𝑧 2 − 4𝑧 − 7.
a) Montrer que si un nombre complexe 𝑧0 est solution de l’équation 𝑔(𝑧) = 0 alors il en est
de même pour son conjugué 𝑧̅0 .
2- Soient 𝑝 et 𝑞 deux entiers relatifs premiers entre eux.
𝑝
a) Montrer que si 𝑞 est solution de l’équation 𝑔(𝑧) = 0, alors 𝑝 divise 7 et 𝑞 divise 3.
b) Déterminer alors un nombre rationnel 𝑧0 solution de l’équation 𝑔(𝑧) = 0.
c) En déduire la résolution dans l’ensemble des nombres complexes de l’équation 𝑔(𝑧) = 0.

Exercice 2 :
ℂ Désigne l’ensemble des nombres complexes.
On pose 𝑧 = 𝑥 + 𝑖𝑦 et 𝑀(𝑥; 𝑦) un point du plan muni d’un repère orthonormé.
1.On considère dans ℂ le polynôme 𝑃(𝑧) = 𝑧 4 + (5𝑖 − 4)𝑧 2 − 6 − 8𝑖.
a) Vérifier que, pour tout nombre complexe 𝑧, 𝑃(𝑧) = (𝑧 2 − 4 + 3𝑖)(𝑧 2 + 2𝑖).
b) Résoudre alors dans ℂ l’équation 𝑃(𝑧) = 0.
𝑧̅ −2+𝑖
2. On considère l’application 𝑓 définie sur ℂ par 𝑓(𝑧) = − −3+𝑖−𝑧̅ .
a) Déterminer la valeur de 𝑧 pour laquelle 𝑓(𝑧) existe.
b) Écrire 𝑓(𝑧) + ̅̅̅̅̅̅
𝑓(𝑧) en fonction de 𝑧 et de 𝑧̅. En déduire alors l’ensemble des points 𝑀(𝑥; 𝑦)
du plan tels que 𝑓(𝑧) soit imaginaire pur.
c) Écrire |𝑓(𝑧)| en fonction de 𝑧. En déduire alors l’ensemble des points (𝑥; 𝑦) du plan tels que
|𝑓(𝑧)| = 1.
𝑖−𝑢
3. 𝑢 désigne un nombre réel 𝑍 est un nombre complexe tel que 𝑍 = 𝑖+𝑢 .
a) Montrer que |𝑍| = 1.

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 4/12

 1−𝑢2 2𝑢
b) Montrer que 𝑍 = 1+𝑢2 + 1+𝑢2 𝑖.
c) Déterminer le réel 𝑢 tel que 𝑅𝑒 (𝑍) = 𝐼𝑚 (𝑍).
√2 √2
d) En déduire alors 𝑢 tel que 𝑍 = + 𝑖.
2 2
Exercice 3 :

Le plan est rapporté à un repère orthonormé 𝓡 = (O ; u ⃗⃗ ; v

⃗⃗ ). On prendra pour unité graphique 3 cm.
2
On considère les points 𝐴 , 𝐵 , 𝐶 et 𝐷 d’affixes respectives 𝑎 = 3 ; 𝑏 = 1 + 3 𝑖 ;
1
𝑐 = 3𝑖 et 𝑑 = − 3 𝑖.
1.) Représenter les points 𝐴 , 𝐵 , 𝐶 et 𝐷 dans le repère 𝓡.
2.) Déterminer l’ange 𝜃 et le rapport 𝑘 de la similitude directe 𝑆 qui transforme 𝐴 en 𝐵 et 𝐶 en 𝐷.
3.) Donner l’écriture complexe de 𝑆 et en déduire l’affixe de son centre Ω.
4.) Soit 𝑀 un point du plan de coordonnées (𝑥 ; 𝑦) et 𝑀’(𝑥 ′ ; 𝑦 ′ ) son image par 𝑆.
1
𝑥′ = − 3 𝑦 + 1
Montrer que : { 1 1 .
𝑦′ = 3 𝑥 − 3
𝑀0 = 𝐴
5.) Soit (𝑀𝑛 )𝑛 ∈ 𝐼𝑁 la suite de points du plan définie par : {
𝑀𝑛 + 1 = 𝑆(𝑀𝑛 ) , ∀ 𝑛 ∈ 𝐼𝑁
Pour tout entier naturel 𝑛, on note 𝑍𝑛 l’affixe du point 𝑀𝑛 et on pose 𝑅𝑛 = | 𝑍𝑛 − 1 |.
a) Montrer que (𝑅𝑛 ) est une suite géométrique dont on précisera le premier terme et la raison.

Exercice 4 :
Le plan complexe est muni d’un repère orthonormé (0; 𝑢 ⃗⃗; 𝑣⃗). Pour tout nombre complexe 𝑧 on pose
𝑝(𝑧) = 𝑧 3 − (4 + 6𝑖)𝑧 2 + (−6 + 16𝑖)𝑧 + 12 − 4𝑖.
1.a) Vérifier que 𝑝(1 + 𝑖) = 0.
b) Déduire en justifiant les solutions dans ℂ de l’équation 𝑝(𝑧) = 0.
2. On considère les points A,B et C su plan d’affixes respectives 𝑧𝐴 = 1 + 𝑖, 𝑧𝐵 = 2 + 2𝑖 et 𝑧𝐶 = 1 + 3𝑖.
a) Montrer qu’il existe une unique similitude directe 𝑠 de centre A, qui transforme C en B.
b) Déterminer l’expression complexe de 𝑠, puis déterminer le rapport et un angle de 𝑠.
3. On considère la transformation 𝑓 qui, à tout point M d’affixe 𝑧, associe le point M’ d’affixe 𝑧′ tel que :
1−𝑖
𝑧 ′ = 2 𝑧 + 𝑖. Pour tout entier naturel 𝑛, on pose 𝑓1 = 𝑓 𝑒𝑡 𝑓 𝑛 = 𝑓 ∘ 𝑓 𝑛−1. On définit la suite de points (𝑀𝑛 )
par 𝑀0 = 𝐶 et 𝑀𝑛 = 𝑓 𝑛 (𝑀0 )
a) Reconnaître la transformation 𝑓 et déterminer ses éléments caractéristiques.
b) Déterminer la nature du triangle 𝐴𝑀𝑛 𝑀𝑛+1.
c) On pose 𝑆𝑛 = 𝑀0 𝑀1 + 𝑀1 𝑀2 + 𝑀2 𝑀3 + ⋯ + 𝑀𝑛 𝑀𝑛+1.
𝑛
√2
i) Montrer que pour tout entier naturel 𝑛 non nul, 𝑀𝑛 𝑀𝑛+1 = ( 2 ) 𝑀0 𝑀1 .
ii)En déduire alors l’expression de 𝑆𝑛 en fonction de 𝑛.
iii) Déduire que la suite (𝑆𝑛 ) vconverge vers 2 + 2√2 puis, interpréter ce résultat.

Exercice 5 :
|𝑧| = |𝑧 − 6|
𝑧 étant un nombre complexe, on note (S) le système suivant :{ 𝜋
𝑎𝑟𝑔(𝑧 2 ) = 2 + 2𝑘𝜋, 𝑘 ∈ ℤ
Le plan complexe 𝑃 est rapporté au repère orthonormé direct (𝑂, 𝑢⃗⃗, 𝑣⃗).
a) Donner le module et un argument des trois complexes suivants :𝑎 = √3 + 𝑖; 𝑏 = −2 + 2𝑖 et 𝑐 = 3 + 3𝑖.
b) Parmi les complexes 𝑎, 𝑏 et 𝑐, lesquels sonts solutions du système (S) ? Justifier votre réponse.
c) M étant un point d’affixe 𝑧, et A étant le point d’affixe 6, traduire géométriquement les deux équations du système (S).
d) Résoudre alors le système (S) par la méthode de votre choix.

Exercice 6 :
On muni le plan d’un repère orthonormé (𝑂, ⃗⃗⃗⃗,
𝑒1 ⃗⃗⃗⃗).
𝑒2 A tout point 𝑀 du plan on associe le point 𝑀′ d’affixe 𝑍 tel que
𝑧 2+1
𝑍 = 2𝑧 . On note 𝑧 = 𝑥 + 𝑖𝑦 et 𝑍 = 𝑋 + 𝑖𝑌 où 𝑥; 𝑦; 𝑋 et 𝑌 sont des nombres réels.
1-a) Exprimer 𝑋 et 𝑌 en fonction de 𝑥 et de 𝑦.
b) Soit 𝑟 un nombre réel strictement positif différent de 1, on suppose que le point 𝑀 appartient au cercle (𝒞) de centre 𝑂
̂ ⃗⃗⃗⃗⃗⃗⃗
et de rayon 𝑟; 𝜃 est un nombre de l’intervalle [0; 2𝜋[ désignant la mesure en radian de l’angle (𝑒⃗⃗⃗⃗,
1 𝑂𝑀 ).
𝑥 = 𝑟𝑐𝑜𝑠𝜃
𝑖) Vérifier que { .
𝑦 = 𝑟𝑠𝑖𝑛𝜃
𝑖𝑖) Déduire de la question (1) les expressions de 𝑋 et de 𝑌 en fonction 𝑟 et de 𝜃.
2-a) Sachant que 𝑐𝑜𝑠 2 𝜃 + 𝑠𝑖𝑛 2 𝜃 = 1, donner une relation indépendante de 𝜃 entre 𝑋 2 et 𝑌 2 .
b) En déduire que lorsque 𝑀 décrit le cercle (𝒞), l’ensemble des point 𝑀′ d’affixe 𝑍 décrit une conique dont on

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 5/12

 précisera la nature.
3) On suppose que 𝑟 = 2 tracer la conique obtenue en faisant apparaître ses foyers et ses directrices.
Exercice 7 :
Le plan est muni d’un repère orthonormé (𝑂 ; ⃗i ; ⃗j ). Soit 𝑓 la transformation du plan qui à tout point 𝑀 de
coordonnées (𝑥 ; 𝑦) du plan associe le point 𝑀’ de coordonnées (𝑥’ ; 𝑦’) tels que :
1 √3
𝑥′ = 4 𝑥 − 𝑦
4
{
√3 1
𝑦′ = 4 𝑥 + 4 𝑦
1. a) Déterminer l’écriture complexe de 𝑓.
b) En déduire la nature et les éléments caractéristiques de 𝑓.
2. Soit () la courbe d’équation 7𝑥 2 + 13𝑦 2 − 6√3𝑥𝑦 − 64 = 0.
a) Déterminer une équation de (′ ) image de () par 𝑓 et déduire la nature et les éléments
caractéristiques de (′ ).
b) Justifier que () est une conique dont on déterminera le centre et les sommets.
c) Construire () et (′ ) dans le même repère.

Exercice 8 :
Le plan est muni d’un repère orthonormé (𝑂, 𝑢⃗⃗, 𝑣⃗).
𝜋
A- Soit (Δ) la droite d’équation 𝑥 = 6 et le point 𝐹(80). Soit 𝜃 ∈ [0; 2 [ et (Γ𝜃 ) l’ensemble des points M du plan vérifiant :
𝑀𝐹 1
= 𝑐𝑜𝑠𝜃 .
𝑑(𝑀(𝐷))
1. Préciser la nature de (Γ𝜃 ) selon les valeurs de 𝜃.
2. Construire (Γ0 ) e donner ses éléments caractéristiques.
3. Donner une équation cartésienne de (Γ𝜋 ), préciser ses éléments caractéristiques et construire (Γ𝜋 ).
6 6
B- À tout point M d’affixe 𝑧 = 𝑥 + 𝑖𝑦 , on associe le point M’ d’affixe 𝑧 ′ = 𝑥 ′ + 𝑖𝑦′, tel que 𝑧 ′ = (3 + 2𝑖)𝑧 + 3𝑖𝑧̅ − 1.
On note (Γ) l’ensemble des points M tels que les points O,M et M’ soient alignés.
1. Donner une équation cartésienne de (Γ).
2. Montrer que (Γ) est une hyperbole dont on précisera les éléments caractéristiques.

THÈME 5 : FONCTIONS LOGARITHMES, FONCTIONS EXPONENTIELLES

,FONCTIONS PUISSANCES ET SUITES NUMÉRIQUES

Exercice 1 :
Soit la fonction 𝑓 définie sur +∞[ par 𝑓(𝑥) = √𝑒 𝑥 − 1.
[0,
On note (𝒞𝑓 ) sa courbe représentative dans un repère orthonormé (𝑂, 𝑖⃗, 𝑗⃗).
𝑓(𝑥)
1- Déterminer lim 𝑓(𝑥) et lim . Interpréter graphiquement ce résultat.
𝑥→+∞ 𝑥→+∞ 𝑥
𝑓(𝑥)
2-a) Montrer que lim+ = +∞. Interpréter graphiquement ce résultat.
𝑥→0 𝑥
𝑒𝑥
b) Montrer que pour tout 𝑥 ∈ ]0, +∞[, 𝑓′(𝑥) = 2√𝑒 𝑥−1.
c) Dresser le tableau de variation de 𝑓.
d) Montrer que le point 𝐵(𝑙𝑛2 1
) est un point d’inflexion de (𝒞𝑓 ).
4- Soit (Υ) la courbe représentative de la fonction : 𝑥 ↦ 𝑒 𝑥 − 1.
a) Étudier la position relative de (𝒞𝑓 ) par rapport à (Υ).
b) Tracer (Υ) puis (𝒞𝑓 ).
Exercice 2 :
On muni le plan d’un repère orthonormal d’origine O et d’unité graphique 4cm. (C) désigne la courbe représentative
de la fonction 𝑓 définie par 𝑓(𝑥) = 𝑙𝑛𝑥 et soit M le point de (C) d’abscisse 𝑥.
1- Montrer que la distance OM de l’origine au point M est telle que OM= √𝑥 2 + (𝑙𝑛𝑥)2.
2 On définit sur ]0; +∞[ la fonction ℎ par ℎ(𝑥) = 𝑥 2 + 𝑙𝑛𝑥.
a) Calculer les limites de ℎ(𝑥) en 0 et en +∞ et déterminer que le sens de variations de ℎ.
1
b) Montrer que l’équation ℎ(𝑥) = 0 admet une unique solution 𝛼 telle que 𝛼 ∈ ] ; 1[.
2
c) En déduire le signe de ℎ(𝑥) suivant les valeurs de 𝑥.
3- On définit sur ]0; +∞[ la fonction 𝑔 par 𝑔(𝑥) = 𝑥 2 + (𝑙𝑛𝑥)2 .
2
a) Pour tout 𝑥 ∈ ]0; +∞[, calculer 𝑔′ (𝑥) et vérifier que 𝑔′ (𝑥) = 𝑥 ℎ(𝑥).
b) En déduire le tableau de variation de 𝑔.

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 6/12

 c) Déduire des questions précédentes la valeur exacte de la distance minimale du point O aux points de la courbe (C) et donner
une valeur approchée de cette distance exprimée en cm, en utilisant la valeur centrale de l’encadrement de 𝛼 trouvée à la
question 2-c).

Exercice 3 :

1- Soient 𝑎 et 𝑏 deux nombres réels strictement positifs tels que 𝑎 < 𝑏.

𝑎+1 𝑏+1
Démontrer que 𝑙𝑛 ( 𝑎 ) > 𝑙𝑛 ( 𝑏 ).
𝑙𝑛𝑥
2- On rappelle que pour tout nombre réel 𝑥 > 0,𝑙𝑜𝑔𝑥 = ,la partie entière d’un nombre réel 𝑥
𝑙𝑛10
est le nombre entier noté 𝐸(𝑥) tel que 𝐸(𝑥) < 𝑥 < 𝐸(𝑥) + 1
L’objectif de cette question est de déterminer le nombre de chiffres de l’écriture décimale de l’entier
premier 𝑁 = 244 497 − 1.
a) Déterminer la partie entière de 𝑙𝑜𝑔𝑁 à l’aide d’une calculatrice.
b) En déduire que 1013 394 < 244 497 < 1013 395 .
c) En déduire un encadrement de 𝑁, puis le nombre de chiffres de l’écriture décimale de l’entier 𝑁.
𝑛
3- Pour tout entier naturel 𝑛 on note 𝑔𝑛 la fonction définie sur ]0; +∞[ par 𝑔𝑛 (𝑥) = 𝑥 − 𝑛 + 2 𝑙𝑛𝑥.
𝑛
a) Justifier que 𝑔𝑛 est dérivable sur ]0; +∞[ et que pour tout 𝑥 ∈ ]0; +∞[, 𝑔𝑛′ (𝑥) = 1 + 2𝑥.
b) Étudier le sens de variation et dresser le tableau de variation de la fonction 𝑔𝑛 .
c) En déduire que l’équation 𝑔𝑛 (𝑥) = 0 admet une unique solution 𝛼𝑛 , dans ]0; +∞[.
2
d) Démontrer que pour tout entier naturel 𝑛, 1 ≤ 𝛼𝑛 ≤ 𝑒 2 , et que 𝑙𝑛(𝛼𝑛 ) = 2 − 𝑛 𝛼𝑛 .
𝛼𝑛
e) Montrer que pour tout entier naturel 𝑛, 𝑔𝑛+1 (𝛼𝑛 ) = − .
𝑛
f) En déduire le sens de variation de la suite (𝛼𝑛 )𝑛∈ℕ∗ .

Exercice 4 :

On se propose de résoudre dans ℝ l’équation (𝐸) : 𝑥 2 + 𝑙𝑛𝑥 − 2 = 0

1. a) Étudier les variations de la fonction 𝑓 définie sur ] 0, + ∞ [ par : 𝑓(𝑥) = 𝑥 2 + 𝑙𝑛𝑥 − 2 et
dresser on tableau de variation.
b) Montrer qu’il existe un unique réel 𝛼 ∈ ] 0, + ∞ [ tel que 𝑓(𝛼) = 0 et en déduire que :
1,30 ≤ 𝛼 ≤ 1,35.
c) Tracer (𝐶𝑓 ) dans le plan muni d’un repère orthonormé ℛ = (O ; ⃗i ; ⃗j ).
d) Démontrer que sur ]0 ; + ∞[, l’équation (𝐸) est équivalent à l’équation 𝑔(𝑥) = 𝑥 𝑜ù 𝑔 est la
fonction définie sur 𝐼 = [1,30 ; 1,35] par 𝑔(𝑥) = √2 − 𝑙𝑛𝑥
2. a) Justifier que 𝑔 est décroissante sur 𝐼 et prouver que, pour tout 𝑥 ∈ 𝐼, 𝑔(𝑥) ∈ 𝐼.
1
b) Montrer que ∀ 𝑥 ∈ 𝐼 , |𝑔′(𝑥)| ≤ 3
1
c) En déduire que pour tout 𝑥 ∈ 𝐼, | 𝑔(𝑥) − 𝛼 | ≤ | 𝑥 − 𝛼 |
3
𝑢 = 1,3
3) Soit (𝑢𝑛 )𝑛 ∈ ℕ la suite d’éléments de 𝐼 définie par : { 0
𝑢𝑛+1 = 𝑔(𝑢𝑛 ) , ∀ 𝑛 ≥ 0
a) Démontrer que pour tout entier naturel 𝑛 , 𝑢𝑛 ∈ 𝐼.
1
b) Démontrer que pour tout 𝑛 ≥ 0 , | 𝑢𝑛 + 1 − 𝛼 | ≤ 3 | 𝑢𝑛 − 𝛼 |
5 1 𝑛
c) En déduire que pour tout 𝑛 ≥ 0 , | 𝑢𝑛 − 𝛼 | ≤ 100 (3 ) et déterminer la limite de la suite(𝑢𝑛 )
d) Déterminer un entier naturel 𝑘 tel que | 𝑢𝑘 − 𝛼 | ≤ 10−6 .
Exercice 5 :
Soit 𝑔 la fonction définie sur ℝ par : 𝑔(𝑥) = (𝑥 + 1)2 𝑒 −𝑥 et (𝐶𝑔 ) sa courbe représentative dans un repère orthonormé
(𝑂 ; 𝑖⃗ ; 𝑗⃗ ). On prendra pour unité graphique sur les axes 2 𝑐𝑚.
1. a) Calculer la dérivée 𝑔’ de 𝑔 et montrer que 𝑔’(𝑥) est du signe de 1 − 𝑥 2 .
b) Dresser le tableau de variation de 𝑔 et vérifier que 0,27 < 𝛼 < 0,28
2) Tracer la courbe (𝐶𝑔 ). On construira en particulier les points de la courbe d’abscisses respectives
−2 ; − 1 ; 0 ; 1 et 3.
3. a) Par lecture graphique, indiquer suivant les valeurs du nombre réel 𝑚 > 0, le nombre et les
signes des solutions de l’équation 𝑔(𝑥) = 𝑚
b) Prouver rigoureusement que l’équation 𝑔(𝑥) = 2 admet une unique solution 𝛼 puis que
𝛼 ∈ [−2 ; −1].
𝛼
c) Montrer que l’on a : 𝛼 = −1 − √2 𝑒 2
𝑥
4°) Soit 𝑓 la fonction définie sur [−2 ; −1] par 𝑓(𝑥) = −1 − √2 𝑒 2
a) Étudier les variations de 𝑓 et montrer que tout élément 𝑥 ∈ 𝐼 = [−2 ; −1] , 𝑓(𝑥) ∈ 𝐼.
1
b) Montrer que : ∀ 𝑥 ∈ 𝐼 , | 𝑓 ′ (𝑥) | ≤ 𝑒
√2
1
c) En déduire que pour tout réel 𝑥 ∈ 𝐼 , | 𝑓(𝑥) − 𝛼 | ≤ 2 | 𝑥 − 𝛼 |

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 7/12

 3
5°) Soit (𝑢𝑛 ) la suite d’éléments de 𝐼 définie par : 𝑢0 = − et 𝑢𝑛+1 = 𝑓(𝑢𝑛 ) ; ∀ 𝑛 ∈ ℕ.
2
1
a) Démontrer que pour tout entier naturel 𝑛 , | 𝑢𝑛 + 1 − 𝛼 | ≤ 2 | 𝑢𝑛 − 𝛼 |
1
b) En déduire que ∀ 𝑛 ∈ ℕ , | 𝑢𝑛 − 𝛼 | ≤ 2𝑛+1
c) Prouver que la suite (𝑢𝑛 ) converge et préciser sa limite.

THÈME 6 : CALCUL DES INTÉGRALES

Exercice 1 :
𝑥 𝑥
Soient la fonction 𝑔 définie sur [1, +∞[ par 𝑔(𝑥) = 𝑒 𝑥−1 et 𝐺 la fonction définie sur [1, +∞[ par 𝐺(𝑥) = ∫1 𝑔(𝑡)𝑑𝑡.
On note (𝒞𝑔 ) sa courbe représentative dans un repère orthonormé (𝑂, 𝑖⃗, 𝑗⃗) d’unité graphique 1𝑐𝑚.
1. a) Justifier que 𝑔 et 𝐺 sont définie sur [1, +∞[.
b) Quelle est la relation qui existe entre 𝑔 et 𝐺?
(1−𝑥)𝑒 𝑥−1
2.a) Montrer que pour tout 𝑥 ∈ [1, +∞[ , 𝑔′(𝑥) = (𝑒 𝑥−1)2
.
b) Calculer lim 𝑔(𝑥), puis interpréter graphiquement ce résultat.
𝑥→+∞
c) Dresser le tableau de variation de 𝑔 sur [1, +∞[ .
d) Représenter (𝒞𝑔 ) sur [1, +∞[.
3.a) Donner une interprétation du nombre 𝐺(3) en termes d’aires.
′
𝑒 𝑥+1
b) Calculer (𝑙𝑛 ( )) .
𝑒𝑥
3 1 1 3
c) Montrer que ∫1 𝑔(𝑡)𝑑𝑡 = 3𝑙𝑛 (1 − 𝑒 3) − 𝑙𝑛 (1 − 𝑒) − ∫1 𝑙𝑛 (1 − 𝑒 −𝑡 )𝑑𝑡.
1 1
d) Montrer que si 1 ≤ 𝑡 ≤ 3 alors 𝑙𝑛 (1 − 𝑒 ) ≤ 𝑙𝑛 (1 − 𝑒 −𝑡 ) ≤ 𝑙𝑛 (1 − 𝑒 3 ).
3
e) En déduire un encadrement de ∫1 𝑙𝑛 (1 − 𝑒 −𝑡 )𝑑𝑡, puis de 𝐻(3).

Exercice 2 :
𝑥
; 𝑠𝑖 𝑥 > 0
𝐴 − ) Soit 𝑓 la fonction définie par : 𝑓(𝑥) = { 𝑥 − ln 𝑥 et (𝐶𝑓 ) sa représentation graphique dans un plan
0 ; 𝑠𝑖 𝑛𝑜𝑛 .
muni du repère orthonormé (O ; 𝑖⃗ ; 𝑗⃗).
1°) Étudier la dérivabilité et la continuité de 𝑓 sur son ensemble de définition.
2°) Étudier 𝑓 et tracer (𝐶𝑓 ). On construira la demi-tangente en 0 et la tangente au point d’abscisse 1.
𝑥
𝐵 − ) On se propose d’étudier la fonction 𝐹 définie par : 𝐹(𝑥) = ∫1 𝑓(𝑡) 𝑑𝑡.
1. a°) Justifier que 𝑓 est 𝐹 est définie et dérivable sur [0 ; + ∞[.
b°) Étudier le sens de variation de 𝐹.
2°) Déterminer le signe de 𝐹 et interpréter graphiquement le résultat.
3. a°) Démontrer que ∀ 𝑡 ∈ [0 ; 1] , 𝑓(𝑡) ≤ 𝑡.
b°) En déduire que :
𝑥2 − 1
i) ∀ 𝑥 ∈ [0,1] , ≤ 𝐹(𝑥) ≤ 0 ;
2
1
ii) − 2 ≤ 𝐹(0) ≤ 0. On ne demande pas la valeur exacte de 𝐹(0).
4. a°) Démontrer que : ∀ 𝑡 [1 ; + ∞ [ ; 1 ≤ 𝑓(𝑡).
b°) En déduire que :
i) ∀ 𝑥 ∈ [0 ; + ∞], 𝑥 – 1 ≤ 𝐹(𝑥) ; ii) lim 𝑓(𝑥) = +∞.
x→∞
ln 𝑡
c) Démontrer que ∀ 𝑥 ∈ [0 ; +∞] , 1 + ≤ 𝑓(𝑡) ≤ 1 + ln 𝑡.
𝑡
𝑙𝑛 (x)2
d) En déduire que ∀ 𝑥 ∈ [0, +∞] , 𝑥 + − 1 ≤ 𝐹(𝑥) ≤ 𝑥𝑙𝑛 𝑥.
2

Exercice 3 :
Dans un plan muni d’un repère orthonormé (O ; 𝑖⃗ ; 𝑗⃗), on considère l’ensemble (𝐸) des points
𝑥+𝑦−8 2
𝑀(𝑥 ; 𝑦) du plan vérifiant la relation : (𝑥 − 2)2 + (𝑦 − 2)2 = ( ) (1)
2
1
𝑥 ′ = 2 (𝑥 + 𝑦)
Soit 𝑓 la transformation du plan d’expression analytique : { 1 (2)
𝑦′ = (−𝑥 + 𝑦)
2
1. a°) Déterminer l’écriture complexe de 𝑓.
b°) Donner la nature et les éléments caractéristiques de 𝑓.
2°) En considérant le point 𝐹 (2 ; 2) et la droite (𝐷) d’équation 𝑥 + 𝑦 – 8 = 0, interpréter
géométriquement les deux membres de l’équation (1) et en déduire que (𝐸) est une conique dont on précisera la nature,
un foyer et une directrice.

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 8/12

 𝑥2 𝑦2
3. a°) Montrer que l’image (𝐸’) de (𝐸) par 𝑓 a pour équation : 8 + 4 = 1.
b) Construire (𝐸’) de (𝐸). On donne l’unité : 2 𝐶𝑚
c) Soit (𝐷) le domaine plan limité par l’ellipse (𝐸’) et les droites d’équation 𝑥 = −2√2 et
𝑥 = 2√2. On fait tourner (𝐷) au tour de l’axe des abscisses et on obtient un solide de révolution appelé (𝑆) ;
Calculer le volume de ce solide.

THÈME 7 : ÉQUATIONS DIFFÉRENTIELLES

Exercice 1 :

On considère l’équation différentielle (E) : 𝑦 ′′ + 2𝑦 ′ + 𝑦 = 2𝑒 −𝑥 .

1. Déterminer le réel 𝜆 pour que la fonction 𝑔 définie sur ℝ par : 𝑔(𝑥) = 𝜆 𝑥 2 𝑒 −𝑥 soit solution de (E) ?
2. Démontrer qu’une fonction 𝑓 deux fois dérivables sur ℝ, est solution de (E) sur ℝ si et seulement si la fonction ℎ
définie sur ℝ par ℎ(𝑥) = 𝑓(𝑥) − 𝑔(𝑥) est solution de l’équation différentielle (E’) : ℎ′′ + 2ℎ′ + ℎ = 0.
3. Soit la fonction 𝑡 = ℎ′ + ℎ. Montrer que 𝑡 ′ + 𝑡 = 0.
4. Résoudre alors sur ℝ l’équation (E’).
5. a) En déduire alors l’ensemble solution de l’équation (E).
b) Déterminer la solution 𝑓 de (E) dont la courbe représentative dans un repère orthonormé (O ; 𝑖⃗ ; 𝑗⃗), , passe
par le point de coordonnées (−1,0) et admet en ce point une tangente de vecteur directeur 𝑖⃗ .

Exercice 2 :
On considère l’équation différentielle (𝐸 ) ∶ 𝑦 ′ − 2𝑦 = (𝑥 − 1) 𝑒 𝑥 .
1. Déterminer les réels 𝑎 et 𝑏 pour que la fonction 𝑓 définie sur ℝ par 𝑓(𝑥) = (𝑎𝑥 + 𝑏) 𝑒 𝑥 soit
solution de (𝐸).
2. Montrer que la fonction 𝑔 est solution de l’équation différentielle (𝐸) si et seulement si
ℎ = 𝑓 − 𝑔 est solution de l’équation différentielle (𝐸0 ) ∶ 𝑦 ′ − 2𝑦 = 0.
3. En déduire toutes les solutions de (𝐸).
4. Trouver la solution 𝑓0 de (𝐸) vérifiant 𝑓0 (0) = 0.
𝑙𝑛3
5. Calculer ∫0 𝑓(𝑥) 𝑑𝑥. On donnera le résultat sous forme 𝑎 + 𝑙𝑛𝑏 où 𝑎 et 𝑏 sont des entiers.

Exercice 3 :
En 2000, une étude est effectuée sur un échantillon de cette population dont l’effectif initial est égal à 1000. Cet échantillon
évolue et son effectif, exprimé en millier d’individus, est approché par une fonction 𝑓 du temps 𝑡 (exprimé en années à partir
de l’origine 2000). D’après le modèle d’évolution choisi, la fonction 𝑓 est dérivable, strictement positive sur [ 0 ; + ∞ [ et
1
satisfait l’équation différentielle (𝐸) : 𝑦 ′ = − 20 𝑦(3 − 𝑙𝑛𝑦).
1. Démontrer l’équivalence suivante : Une fonction 𝑓, dérivable, strictement positive sur [ 0 ; + ∞ [, vérifie pour tout 𝑡 ∈
1
[ 0 ; + ∞ [ , 𝑓′(𝑡) = − 20 𝑓(𝑡)[ 3 − 𝑙𝑛(𝑓(𝑡)) ] si et seulement si la fonction
1 3
𝑔 = 𝑙𝑛(𝑓) vérifie, pour tout 𝑡 ∈ [ 0 ; + ∞ [ , 𝑔′ (𝑡) = 20 𝑔(𝑡) − 20.
1 3
2. Donner la solution générale de l’équation différentielle (𝐻) : 𝑧′ = 20 𝑧 − 20.
𝑡
3. En déduire qu’il existe un réel 𝑘 tel que pour tout 𝑡 ∈ [ 0 ; + ∞ [ , 𝑓(𝑡) = 𝑒𝑥𝑝 (3 + 𝑘 𝑒𝑥𝑝 (20)) ;
Où la notation 𝑒𝑥𝑝 désigne la fonction exponentielle.
4. La condition initiale conduit donc à considérer la fonction 𝑓 définie par :
𝑡
𝑓(𝑡) = 𝑒𝑥𝑝 (3 − 3 𝑒𝑥𝑝 (20)).
a) Déterminer la limite de la fonction 𝑓 en + ∞.
b) Déterminer le sens de variation de 𝑓 sur [ 0 ; + ∞ [.
c) Résoudre dans [ 0 ; + ∞ [ l’inéquation 𝑓(𝑡) ≤ 0,02.
d) Au bout de combien d’années, selon ce modèle, la taille de l’échantillon sera-t-elle inférieur à
20 individus ?

THÈME 8 : PROBABILITÉS
Exercice 1 :
A. Une urne contient un jeton qui portent le nombre 2, un jeton qui portent le nombre 3 , un jetons qui portent
1
le nombre 5, deux jetons qui portent le nombre 𝑒 et un jeton qui portent le nombre 𝑒.
Tous les jetons sont indiscernables au toucher.
On tire successivement avec remise deux jetons de l’urne et on note par 𝑎 et 𝑏 les nombres lus, respectivement
sur le premier et le deuxième jeton tirés.
A cette expérience, on associe le point M d’affixe 𝑧 = 𝑙𝑛 𝑎 + 𝑖 𝑙𝑛 𝑏 , on considère les vecteurs

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 9/12

 𝑏
𝑒⃗ (𝑎1) et 𝑓⃗ (1) ; et on note 𝑑 = 𝑝𝑔𝑐𝑑(𝑎; 𝑏) lorsque 𝑎 et 𝑏 sont des entiers.
1 𝑏
Le plan complexe est muni d’un repère (0, 𝑢 ⃗⃗, 𝑣⃗) orthonormé tandis que l’espace est muni d’une base
⃗⃗
orthonormée (𝑖⃗, 𝑗⃗, 𝑘 ).
Calculer la probabilité des évènements suivants :
a) A : « M appartient à l’axe des abscisses ».
̂
⃗⃗⃗⃗⃗⃗⃗ 𝜋
b) B : « L’angle ( 𝑂𝑀 ;𝑢
⃗⃗ ) est − ».
4
c) C : « 𝑎 et 𝑏 sont premiers entre eux ».
d) D : « 𝑒⃗ et 𝑓⃗ sont colinéaires ».
B. On considère un dé parfaitement équilibré à cinq faces et les cinq faces portent nombres suivants:
𝑖; 2𝑖; √3 + 𝑖; √3 − 𝑖 𝑒𝑡 − 3
On lance ce dé et on note 𝑧 le nombre qui apparait sur sa face supérieure.
1.On lance 5 fois de suite ce même dé. Calculer la probabilité d’obtenir 4 fois la réalisation de l’évènement
E: « 𝑧 est imaginaire pur ».
2. On définit la variable aléatoire 𝜃 qui, à chaque nombre 𝑧 inscrit sur une face, associe son argument principal.
𝜋 𝜋 𝜋
a. Vérifier que 𝜃 ∈ {− ; ; ; 𝜋}.
6 6 2
b. Déterminer la loi de probabilité de 𝜃.
c. Calculer son espérance mathématique 𝐸(𝜃).

Exercice 2 :
Étant donné un espace probabilisé Ω, on considère une variable aléatoire 𝑋sur Ω prenant les valeurs
𝑥1 ; 𝑥2 ; 𝑥3 ; 𝑥4 et 𝑥5 rangées dans l’ordre croissant.
1) Comment choisir le réel 𝑎 pour que le tableau suivant définisse une loi de probabilité de 𝑋 ?
𝑥𝑘 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5
𝑝𝑘 𝑎 𝑎 4𝑎 5𝑎
2𝑎
2 2
2) Le réel a étant ainsi choisi, on donne 𝑥4 = 7. Déterminer 𝑥1 ; 𝑥2 ; 𝑥3 et 𝑥5 tel que
(𝑥1 ; 𝑥2 ; 𝑥3 ; 𝑥4 ; 𝑥5 ) soit une suite arithmétique et que l’espérance de 𝑋 soit 5,8.
3 Déterminer alors la fonction de répartition de 𝑋 ainsi que son écart-type.

Exercice 3 :
Un commerçant constate que parmi les clients qui achètent un melon une semaine donnée, 90 % d’entre eux
achètent un melon la semaine suivante. Parmi les clients qui n’achètent pas de melon une semaine donnée 60 %
d’entre eux n’achètent pas de melon la semaine suivante. On choisit au hasard un client ayant acheté un melon au
cours de la semaine 1 et pour tout entier naturel 𝒏 > 𝟏, on note 𝑨𝒏 l’événement « le client achète un melon au cours
de la semaine 𝒏 » et 𝑷𝒏 = 𝑷(𝑨𝒏 ) sa probabilité. On a alors 𝑷𝟏 = 𝟏.
1. Démontrer que 𝑃3 = 0,85.
2. Sachant que le client achète un melon la semaine 3, quelle est la probabilité qu’il en ait acheté la deuxième
semaine ?
3. Démontrer que pour tout entier 𝑛 ≥ 1 : Pn+1 = 0,5 Pn + 0,4.
4. Démontrer par récurrence que pour tout entier n ≥ 1, Pn ≥ 0,8.
5. En déduire que la suite (𝑃𝑛 ) est décroissante. La suite (𝑃𝑛 ) est-elle convergente ?
6. On pose pour tout entier 𝑛 ≥ 1 𝑉𝑛 = 𝑃𝑛 − 0,8. Démontrer que (𝑉𝑛 ) est une suite géométrique.
7. a) Exprimer 𝑉𝑛 puis 𝑃𝑛 en fonction de 𝑛.
b) En déduire la limite de (𝑃𝑛 ).

Exercice 4 :
Soit 𝑛 un entier naturel supérieur à 1. On considère une urne dans laquelle se trouve une boule portant le numéro 1 ;
deux boules portant le numéro 2 ; trois boules portant le numéro 3 ; … ; 𝑛 boules portant le numéro 𝑛.
1) Combien l’urne contient-elle de boules ?
𝑥2 𝑦2
2) On considère l’hyperbole (𝐻) d’équation 𝑎2 − 𝑏 2 = 1 ; pour déterminer 𝑎 et 𝑏, on tire successivement et avec remise
deux boules de l’urne. Calculer la probabilité pour que (𝐻) soit une hyperbole équilatère.
𝑛 (𝑛 + 1) (2𝑛 + 1)
(On rappelle que ∑𝑛𝑘=0 𝑘 2 = ).
6

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 10/12

 THÈME 9 : STATISTIQUES

Exercice 1 :
Sur huit exploitations agricoles d’une même région ,on a mesuré la taille de l’exploitation en hectare (ℎ𝑎) et le
bénéfice annuel en Francs . Les résultats sont regroupés dans le tableau ci-dessous .
Taille X 1 2 4 1 3 4 3 2
Bénéfice Y 2 5 7 -1 8 9 7 3

1) Déterminer les coordonnées du point moyen G .

2) Calculer le coefficient de corrélation linéaire .
3) Un ajustement linéaire est-il approprié ? justifier votre réponse.
4) Déterminer une équation de la droite de régression de 𝑦 𝑒𝑛 𝑥.
5) Quel serait le bénéfice d’une exploitation de 2,5ℎ𝑎 ?

Exercice 2 :
Le tableau ci-dessous indique pour Année 2016 2017 2018 2019 2020 2021 2022
chaque année le nombre de milliers
𝑋𝑖 0 1 2 3 4 5 6
de mariages célébrés dans une région.
𝑋𝑖 désigne le rang de de l’année et 𝑌𝑖 𝑌𝑖 395 374 a 334 312 b 266
désigne le nombre de mariages (en milliers).
Dans la direction des statistiques, certaines données ont été effacées. Ce pendant , ces valeurs
avaient permis par la méthode des moindres carrées d’obtenir la droite de régression de Y en X
dont l’équation réduite est la suivante : (D) : 𝑌 = −22𝑋 + 397.
1) Quel est le signe du coefficient de corrélation ainsi que celui de la covariance ? Justifier.
2) Calculer la moyenne et la variance de X.
𝑎+𝑏+1681
3) Vérifier que 𝑌̅ = .
7
−𝑎+2𝑏−823
4) Démontrer que 𝑐𝑜𝑣(𝑋, 𝑌) = .
7
5) En déduire les valeurs de a et de b.
6) déterminer une équation de la droite de régression de X en Y.

THÈME 10 : ISOMÉTRIES DE L’ESPACE

Exercice 1 :
A-Soit ABCDA′B′C′D′ un cube (Voir figure ci-contre). On désigne par :
s1 la réflexion de base le plan (AA′B′).
s2 la réflexion de base le plan (BB′C’).
s3 la réflexion de base (CC′D).
s4 la réflexion de base le plan (DD′A).
1. a) Montrer que r = s2 ◦ s1 est un demi-tour dont on précisera l’axe.
b) Déterminer la nature et les éléments géométriques caractéristiques de r′ = s 4 ◦ s3.
2. On note s la réflexion de base le plan (BB′D).
a) Déterminer les réflexions s′ et s′′ telles que r = s∘s′ et r′ = s’’∘ s.
b) En déduire que t = r′∘r est la translation de vecteur 2𝐵𝐷 ⃗⃗⃗⃗⃗⃗⃗ .
B- On muni l’espace d’un repère orthonormée directe (𝑂, 𝑖⃗, 𝑗⃗, 𝑘 ⃗⃗ ).
On considère le plan (𝑃) : 2𝑥 + 8𝑦 − 6𝑧 = 0 et (𝑃′) : 7𝑥 − 𝑦 + 𝑧 − 5 = 0 et la droite (𝑑) passant
par le point 𝐾(1; 0; −1) et dirigée par le vecteur 𝑢⃗⃗ = 𝑖⃗ + 𝑗⃗ + 𝑘 ⃗⃗ .
1. Déterminer l’expression analytique de la réflexion d’axe le plan (𝑃).
2. Déterminer l’expression analytique du demi-tour d’axe la droite (𝑑).
3. a) Montrer que (P) et (P’) sont orthogonaux suivant une droite à déterminer.
b) En déduire la nature et l’élément caractéristique de 𝑆(𝑃) ∘ 𝑆(𝑃′) .

Exercice 1 :
1) Déterminer l’expression analytique de la réflexion du plan (𝑃): 2𝑥 − 3𝑦+′ 𝑧 − 7 = 0.
2) Soit 𝑓 l’application de l’espace dans lui-même qui à un point 𝑀(𝑧, 𝑦, 𝑧), on associe le
1
𝑥 ′ = (−2𝑥 − 3𝑦 + 6𝑧 − 3)
7
′ 1
point 𝑀′(𝑥′, 𝑦′, 𝑧 ′ ) tel que 𝑦 = 7 (−3𝑥 + 6𝑦 + 2𝑧 − 1)
′ 1
(6𝑥 + 2𝑦 + 3𝑧 + 2)
{ 𝑧 =7

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 11/12

 a) Déterminer l’ensemble des points invariants (𝜋) de l’application 𝑓. b) Soient M et M’ deux points de
l’espace tels que 𝑓(𝑀) = 𝑀′ .
Démontrer que :
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗est normal à (𝜋).
𝑖) Le vecteur 𝑀𝑀′
𝑖𝑖) Le point I milieu du segment [MM’] appartient à(𝜋).
c) En déduire la nature et les éléments caractéristiques de 𝑓.
3) ABCDEFGH est un cube. I, J, K et L, les
milieux respectifs des segments [AE] ; [BF] ; [DH] et [CG].
Déterminer la nature et les éléments caractéristiques des transformations suivantes :
a) 𝑆(𝐴𝐷𝐾) ∘ (𝐼𝐸𝐻).
b) 𝑆(𝐴𝐵𝐶) ∘ (𝐼𝐽𝐿).
c) 𝑆(𝐴𝐷𝐵) ∘ (𝐸𝐹𝐻).

GSMA_CHRONO 2_MATHS_TLE C_PPSD PAGE 12/12