Académique Documents
Professionnel Documents
Culture Documents
Vusosolabewiv
Transféré par
jhdgame7Titre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Vusosolabewiv
Transféré par
jhdgame7Droits d'auteur :
Formats disponibles
Intégrale double coordonnées polaires exercices corrigés pdf
En raison de limitations techniques, la typographie souhaitable du titre, « Exercice : Calculs d'intégrales doublesIntégrale double/Exercices/Calculs d'intégrales doubles », n'a pu être restituée correctement ci-dessus.
Exercice 1-1[modifier | modifier le wikicode] Calculer ∬ [ 0 , 1 ] × [ 0 , π 2 [ d x d y 1 + x 2 tan 2 y {\displaystyle \iint _{\left[0,1\right]\times \left[0,{\frac {\pi }{2}}\right[}{\frac {\mathrm {d} x\,\mathrm {d} y}{1+x^{2}\tan ^{2}y}}} ; ∬ [ 0 , 1 ] 2 d x d y ( x + y + 1 ) 2 {\displaystyle \iint _{\left[0,1\right]^{2}}{\frac {\mathrm {d} x\,\mathrm {d}
y}{(x+y+1)^{2}}}} ; ∬ [ − 1 , 1 ] × [ 1 , 2 ] x 2 y d x d y {\displaystyle \iint _{\left[-1,1\right]\times \left[1,2\right]}{\frac {x^{2}}{y}}\,\mathrm {d} x\,\mathrm {d} y} ; ∬ [ 0 , π 2 ] × [ 0 , π 2 ] sin ( x + y ) d x d y {\displaystyle \iint _{\left[0,{\frac {\pi }{2}}\right]\times \left[0,{\frac {\pi }{2}}\right]}\sin(x+y)\,\mathrm {d} x\,\mathrm {d} y} ; ∬
[ 3 , 7 ] × [ − 2 , 2 ] x 1 + x y + x 2 d x d y {\displaystyle \iint _{\left[3,7\right]\times \left[-2,2\right]}{\frac {x}{\sqrt {1+xy+x^{2}}}}\,\mathrm {d} x\,\mathrm {d} y} . Exercice 1-2[modifier | modifier le wikicode] Calculer : si D {\displaystyle D} est le triangle x , y ≥ 0 , x + y ≤ 1 {\displaystyle x,y\geq 0,\;x+y\leq 1} : ∬ D ( x 2 + y 2 ) d x d y
{\displaystyle \iint _{D}(x^{2}+y^{2})\,\mathrm {d} x\,\mathrm {d} y} , ∬ D x y ( x + y ) d x d y {\displaystyle \iint _{D}xy(x+y)\,\mathrm {d} x\,\mathrm {d} y} , ∬ D ( x + y ) e − x e − y d x d y {\displaystyle \iint _{D}(x+y)\operatorname {e} ^{-x}\operatorname {e} ^{-y}\,\mathrm {d} x\,\mathrm {d} y} ; ∬ D x d x d y 1 + x 2 + y 2
{\displaystyle \iint _{D}{\frac {x\,\mathrm {d} x\,\mathrm {d} y}{\sqrt {1+x^{2}+y^{2}}}}} où D {\displaystyle D} est le domaine défini par 0 ≤ y 2 ≤ 2 x ≤ 4 {\displaystyle 0\leq y^{2}\leq 2x\leq 4} ; ∬ D x y 1 + x 2 + y 2 d x d y {\displaystyle \iint _{D}{\frac {xy}{1+x^{2}+y^{2}}}\,\mathrm {d} x\,\mathrm {d} y} où D = { ( x , y ) ∈ [ 0 , 1 ] 2
∣ x 2 + y 2 ≥ 1 } {\displaystyle D=\{(x,y)\in [0,1]^{2}\mid x^{2}+y^{2}\geq 1\}} ; ∬ D ( x + y ) sin x sin y d x d y {\displaystyle \iint _{D}(x+y)\sin x\sin y\,\mathrm {d} x\,\mathrm {d} y} où D {\displaystyle D} est le triangle x , y ≥ 0 , x + y ≤ π {\displaystyle x,y\geq 0,\;x+y\leq \pi } ; ∬ D ( x + y ) d x d y {\displaystyle \iint _{D}(x+y)\,\mathrm {d}
x\,\mathrm {d} y} où D = { ( x , y ) ∈ R 2 ∣ 1 ≥ x ≥ 0 , x 2 ≤ y ≤ x } {\displaystyle D=\{(x,y)\in \mathbb {R} ^{2}\mid 1\geq x\geq 0,\;x^{2}\leq y\leq x\}} ; ∬ D d x d y ( x + y ) 3 {\displaystyle \iint _{D}{\frac {\mathrm {d} x\,\mathrm {d} y}{(x+y)^{3}}}} où D = { ( x , y ) ∈ R 2 ∣ 3 > x > 1 , y > 2 , x + y < 5 } {\displaystyle D=\{(x,y)\in \mathbb
{R} ^{2}\mid 3>x>1,\;y>2,\;x+y<5\}} ; ∬ D cos ( x y ) d x d y {\displaystyle \iint _{D}\cos(xy)\,\mathrm {d} x\,\mathrm {d} y} où D = { ( x , y ) ∈ R 2 ∣ 2 ≥ x ≥ 1 , 0 ≤ x y ≤ 2 } {\displaystyle D=\{(x,y)\in \mathbb {R} ^{2}\mid 2\geq x\geq 1,\;0\leq xy\leq 2\}} ; ∬ D x d x d y {\displaystyle \iint _{D}x\,\mathrm {d} x\,\mathrm {d} y} où D = { ( x , y
) ∈ R 2 ∣ y ≥ 0 , x − y + 1 ≥ 0 , x + 2 y − 4 ≤ 0 } {\displaystyle D=\{(x,y)\in \mathbb {R} ^{2}\mid y\geq 0,\;x-y+1\geq 0,\;x+2y-4\leq 0\}} ; ∬ D x y d x d y {\displaystyle \iint _{D}xy\,\mathrm {d} x\,\mathrm {d} y} où D = { ( x , y ) ∈ R 2 ∣ x , y ≥ 0 , x y + x + y ≤ 1 } {\displaystyle D=\{(x,y)\in \mathbb {R} ^{2}\mid x,y\geq 0,\;xy+x+y\leq 1\}} .
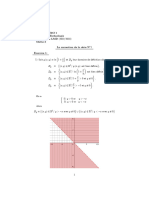
Exercice 1-3[modifier | modifier le wikicode] On considère le domaine plan D = { ( x , y ) ∈ R 2 ∣ x ≥ 0 , 2 x 2 ≤ y ≤ 3 } {\displaystyle D=\{\left(x,y\right)\in \mathbb {R} ^{2}\mid x\geq 0,\;2x^{2}\leq y\leq 3\}} et la surface S = { ( x , y , z ) ∈ R 3 ∣ ( x , y ) ∈ D , z = x + y } {\displaystyle S=\{\left(x,y,z\right)\in \mathbb {R} ^{3}\mid \left(x,y\right)\in
D,\;z=x+y\}} . Dessiner D {\displaystyle D} et calculer son aire et son périmètre. Déterminer le centre d'inertie (ou centre de gravité) G {\displaystyle G} de D {\displaystyle D} , défini par ( ∬ D 1 d x d y ) O G → = ∬ D O M → d x d y {\displaystyle \left(\iint _{D}1\,\mathrm {d} x\,\mathrm {d} y\right){\overrightarrow {OG}}=\iint _{D}
{\overrightarrow {OM}}\,\mathrm {d} x\,\mathrm {d} y} . Calculer ∬ D ( x + y ) d x d y {\displaystyle \iint _{D}\left(x+y\right)\,\mathrm {d} x\,\mathrm {d} y} . Quelle en est l'interprétation en termes de volume ? Déterminer l'aire de S {\displaystyle S} . Pour k > 1 {\displaystyle k>1} , déterminer le centre de gravité ( x k , y k ) {\displaystyle
(x_{k},y_{k})} du trapèze D k {\displaystyle D_{k}} de sommets ( 0 , 0 ) {\displaystyle (0,0)} , ( 1 , 0 ) {\displaystyle (1,0)} , ( 1 , 1 ) {\displaystyle (1,1)} et ( 0 , k ) {\displaystyle (0,k)} . Pour tout domaine D ⊂ R 2 {\displaystyle D\subset \mathbb {R} ^{2}} et toute application affine inversible φ : R 2 → R 2 {\displaystyle \varphi :\mathbb {R}
^{2}\to \mathbb {R} ^{2}} , montrer que le centre de gravité de φ ( D ) {\displaystyle \varphi (D)} est φ ( G ) {\displaystyle \varphi (G)} , où G {\displaystyle G} désigne le centre de gravité de D {\displaystyle D} . En déduire que si D {\displaystyle D} est symétrique par rapport à un point O {\displaystyle O} alors G = O {\displaystyle G=O} .
Exercice 1-4[modifier | modifier le wikicode] Dessiner le domaine D = { ( x , y ) ∈ R 2 ∣ 0 ≤ x ≤ y , x 2 + y 2 ≤ 1 } {\displaystyle D=\{\left(x,y\right)\in \mathbb {R} ^{2}\mid 0\leq x\leq y,\;x^{2}+y^{2}\leq 1\}} .
Calculer ∬ D ( x + y ) d x d y {\displaystyle \iint _{D}\left(x+y\right)\,\mathrm {d} x\mathrm {d} y} a) par calcul direct ; b) en passant en coordonnées polaires. Exercice 1-5[modifier | modifier le wikicode] Soient : D {\displaystyle D} le triangle de sommets ( 0 , 0 ) {\displaystyle (0,0)} , ( 1 , 0 ) {\displaystyle (1,0)} et ( 0 , 1 ) {\displaystyle (0,1)} ; Φ :
R 2 → R 2 , ( x , y ) ↦ ( u , v ) = ( 2 x + y , x − y ) {\displaystyle \Phi :\mathbb {R} ^{2}\to \mathbb {R} ^{2},\,(x,y)\mapsto (u,v)=(2x+y,x-y)} ; Δ = Φ ( D ) {\displaystyle \Delta =\Phi (D)} . Expliquer pourquoi Δ {\displaystyle \Delta } est un triangle et préciser ses sommets. En utilisant un changement de variables, justifier l'égalité ∬ Δ e u v d u d v =
3 ∬ D e ( 2 x + y ) ( x − y ) d x d y {\displaystyle \iint _{\Delta }\mathrm {e} ^{uv}\;\mathrm {d} u\mathrm {d} v=3\iint _{D}\mathrm {e} ^{(2x+y)(x-y)}\;\mathrm {d} x\mathrm {d} y} (sans calculer les intégrales en question). Exercice 1-6[modifier | modifier le wikicode] Soit D = { ( x , y ) ∈ R 2 ∣ 0 ≤ x ≤ y ≤ 1 } {\displaystyle D=\{(x,y)\in \mathbb
{R} ^{2}\mid 0\leq x\leq y\leq 1\}} . Représenter graphiquement D {\displaystyle D} et calculer ∬ D x y d x d y {\displaystyle \iint _{D}xy\;\mathrm {d} x\mathrm {d} y} . Soit Ω = { ( x , y ) ∈ R 2 ∣ 0 ≤ y ≤ 1 , 0 ≤ x ≤ y } {\displaystyle \Omega =\{(x,y)\in \mathbb {R} ^{2}\mid 0\leq y\leq 1,\;0\leq x\leq {\sqrt {y}}\}} .
Pour k > 1 {\displaystyle k>1} , déterminer le centre de gravité ( x k , y k ) {\displaystyle (x_{k},y_{k})} du trapèze D k {\displaystyle D_{k}} de sommets ( 0 , 0 ) {\displaystyle (0,0)} , ( 1 , 0 ) {\displaystyle (1,0)} , ( 1 , 1 ) {\displaystyle (1,1)} et ( 0 , k ) {\displaystyle (0,k)} . Pour tout domaine D ⊂ R 2 {\displaystyle D\subset \mathbb {R} ^{2}} et
toute application affine inversible φ : R 2 → R 2 {\displaystyle \varphi :\mathbb {R} ^{2}\to \mathbb {R} ^{2}} , montrer que le centre de gravité de φ ( D ) {\displaystyle \varphi (D)} est φ ( G ) {\displaystyle \varphi (G)} , où G {\displaystyle G} désigne le centre de gravité de D {\displaystyle D} . En déduire que si D {\displaystyle D} est symétrique
par rapport à un point O {\displaystyle O} alors G = O {\displaystyle G=O} . Exercice 1-4[modifier | modifier le wikicode] Dessiner le domaine D = { ( x , y ) ∈ R 2 ∣ 0 ≤ x ≤ y , x 2 + y 2 ≤ 1 } {\displaystyle D=\{\left(x,y\right)\in \mathbb {R} ^{2}\mid 0\leq x\leq y,\;x^{2}+y^{2}\leq 1\}} .
En déduire que si D {\displaystyle D} est symétrique par rapport à un point O {\displaystyle O} alors G = O {\displaystyle G=O} . Exercice 1-4[modifier | modifier le wikicode] Dessiner le domaine D = { ( x , y ) ∈ R 2 ∣ 0 ≤ x ≤ y , x 2 + y 2 ≤ 1 } {\displaystyle D=\{\left(x,y\right)\in \mathbb {R} ^{2}\mid 0\leq x\leq y,\;x^{2}+y^{2}\leq 1\}} . Calculer
∬ D ( x + y ) d x d y {\displaystyle \iint _{D}\left(x+y\right)\,\mathrm {d} x\mathrm {d} y} a) par calcul direct ; b) en passant en coordonnées polaires. Exercice 1-5[modifier | modifier le wikicode] Soient : D {\displaystyle D} le triangle de sommets ( 0 , 0 ) {\displaystyle (0,0)} , ( 1 , 0 ) {\displaystyle (1,0)} et ( 0 , 1 ) {\displaystyle (0,1)} ; Φ : R 2 → R
2 , ( x , y ) ↦ ( u , v ) = ( 2 x + y , x − y ) {\displaystyle \Phi :\mathbb {R} ^{2}\to \mathbb {R} ^{2},\,(x,y)\mapsto (u,v)=(2x+y,x-y)} ; Δ = Φ ( D ) {\displaystyle \Delta =\Phi (D)} . Expliquer pourquoi Δ {\displaystyle \Delta } est un triangle et préciser ses sommets. En utilisant un changement de variables, justifier l'égalité ∬ Δ e u v d u d v = 3 ∬ D e (
2 x + y ) ( x − y ) d x d y {\displaystyle \iint _{\Delta }\mathrm {e} ^{uv}\;\mathrm {d} u\mathrm {d} v=3\iint _{D}\mathrm {e} ^{(2x+y)(x-y)}\;\mathrm {d} x\mathrm {d} y} (sans calculer les intégrales en question). Exercice 1-6[modifier | modifier le wikicode] Soit D = { ( x , y ) ∈ R 2 ∣ 0 ≤ x ≤ y ≤ 1 } {\displaystyle D=\{(x,y)\in \mathbb {R}
^{2}\mid 0\leq x\leq y\leq 1\}} .
Quelle en est l'interprétation en termes de volume ? Déterminer l'aire de S {\displaystyle S} . Pour k > 1 {\displaystyle k>1} , déterminer le centre de gravité ( x k , y k ) {\displaystyle (x_{k},y_{k})} du trapèze D k {\displaystyle D_{k}} de sommets ( 0 , 0 ) {\displaystyle (0,0)} , ( 1 , 0 ) {\displaystyle (1,0)} , ( 1 , 1 ) {\displaystyle (1,1)} et ( 0 , k )
{\displaystyle (0,k)} . Pour tout domaine D ⊂ R 2 {\displaystyle D\subset \mathbb {R} ^{2}} et toute application affine inversible φ : R 2 → R 2 {\displaystyle \varphi :\mathbb {R} ^{2}\to \mathbb {R} ^{2}} , montrer que le centre de gravité de φ ( D ) {\displaystyle \varphi (D)} est φ ( G ) {\displaystyle \varphi (G)} , où G {\displaystyle G} désigne
le centre de gravité de D {\displaystyle D} . En déduire que si D {\displaystyle D} est symétrique par rapport à un point O {\displaystyle O} alors G = O {\displaystyle G=O} . Exercice 1-4[modifier | modifier le wikicode] Dessiner le domaine D = { ( x , y ) ∈ R 2 ∣ 0 ≤ x ≤ y , x 2 + y 2 ≤ 1 } {\displaystyle D=\{\left(x,y\right)\in \mathbb {R} ^{2}\mid
0\leq x\leq y,\;x^{2}+y^{2}\leq 1\}} . Calculer ∬ D ( x + y ) d x d y {\displaystyle \iint _{D}\left(x+y\right)\,\mathrm {d} x\mathrm {d} y} a) par calcul direct ; b) en passant en coordonnées polaires. Exercice 1-5[modifier | modifier le wikicode] Soient : D {\displaystyle D} le triangle de sommets ( 0 , 0 ) {\displaystyle (0,0)} , ( 1 , 0 ) {\displaystyle
(1,0)} et ( 0 , 1 ) {\displaystyle (0,1)} ; Φ : R 2 → R 2 , ( x , y ) ↦ ( u , v ) = ( 2 x + y , x − y ) {\displaystyle \Phi :\mathbb {R} ^{2}\to \mathbb {R} ^{2},\,(x,y)\mapsto (u,v)=(2x+y,x-y)} ; Δ = Φ ( D ) {\displaystyle \Delta =\Phi (D)} . Expliquer pourquoi Δ {\displaystyle \Delta } est un triangle et préciser ses sommets. En utilisant un changement de
variables, justifier l'égalité ∬ Δ e u v d u d v = 3 ∬ D e ( 2 x + y ) ( x − y ) d x d y {\displaystyle \iint _{\Delta }\mathrm {e} ^{uv}\;\mathrm {d} u\mathrm {d} v=3\iint _{D}\mathrm {e} ^{(2x+y)(x-y)}\;\mathrm {d} x\mathrm {d} y} (sans calculer les intégrales en question). Exercice 1-6[modifier | modifier le wikicode] Soit D = { ( x , y ) ∈ R 2 ∣ 0 ≤ x
≤ y ≤ 1 } {\displaystyle D=\{(x,y)\in \mathbb {R} ^{2}\mid 0\leq x\leq y\leq 1\}} . Représenter graphiquement D {\displaystyle D} et calculer ∬ D x y d x d y {\displaystyle \iint _{D}xy\;\mathrm {d} x\mathrm {d} y} . Soit Ω = { ( x , y ) ∈ R 2 ∣ 0 ≤ y ≤ 1 , 0 ≤ x ≤ y } {\displaystyle \Omega =\{(x,y)\in \mathbb {R} ^{2}\mid 0\leq y\leq 1,\;0\leq x\leq
{\sqrt {y}}\}} . Calculer ∬ Ω x y d x d y {\displaystyle \iint _{\Omega }xy\;\mathrm {d} x\mathrm {d} y} . Exercice 1-7[modifier | modifier le wikicode] Calculer : ∬ x 2 + y 2 ≤ 1 ( x 2 + y 2 ) d x d y {\displaystyle \iint _{x^{2}+y^{2}\leq 1}\left(x^{2}+y^{2}\right)\;\mathrm {d} x\mathrm {d} y} ; ∬ x , y ≥ 0 x 2 + y 2 ≤ 1 ( 4 − x 2 − y 2 ) d x d y
{\displaystyle \iint _{x,y\geq 0 \atop x^{2}+y^{2}\leq 1}\left(4-x^{2}-y^{2}\right)\;\mathrm {d} x\mathrm {d} y} ; ∬ x ≥ 0 x 2 + y 2 ≤ 1 x e ( x 2 + y 2 ) 3 / 2 d x d y {\displaystyle \iint _{x\geq 0 \atop x^{2}+y^{2}\leq 1}x\operatorname {e} ^{(x^{2}+y^{2})^{3/2}}\;\mathrm {d} x\mathrm {d} y} ; ∬ π 2 < x 2 + y 2 ≤ 4 π 2 sin x 2 + y 2 d x d
y {\displaystyle \iint _{\pi ^{2} 0 x 2 a 2 + y 2 b 2 ≤ 1 x y d x d y {\displaystyle \iint _{x,y>0 \atop {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}\leq 1}xy\;\mathrm {d} x\mathrm {d} y} ; ∬ y < x 2 + y 2 < x ( x 2 + y 2 ) d x d y {\displaystyle \iint _{y 0 d x d y {\displaystyle \iint _{{\frac {1}{2}}0}\mathrm {d} x\mathrm {d} y} ; ∬ x 2 + y 2 −
2 x ≤ 0 x 2 + y 2 d x d y {\displaystyle \iint _{x^{2}+y^{2}-2x\leq 0}{\sqrt {x^{2}+y^{2}}}\;\mathrm {d} x\mathrm {d} y} et ∬ x ≥ 0 1 ≤ x 2 + y 2 ≤ 2 y x 2 + y 2 d x d y {\displaystyle \iint _{x\geq 0 \atop 1\leq x^{2}+y^{2}\leq 2y}{\sqrt {x^{2}+y^{2}}}\;\mathrm {d} x\mathrm {d} y} .
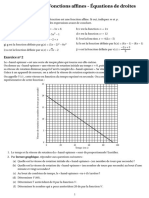
Exercice 1-8[modifier | modifier le wikicode] Représenter graphiquement l'ensemble D = { ( x , y ) ∈ R 2 ∣ 0 ≤ y ≤ 1 − x 2 } {\displaystyle D=\{(x,y)\in \mathbb {R} ^{2}\mid 0\leq y\leq 1-x^{2}\}} puis calculer ∬ D x d x d y {\displaystyle \iint _{D}x\;\mathrm {d} x\mathrm {d} y} , ∬ D y d x d y {\displaystyle \iint _{D}y\;\mathrm {d} x\mathrm {d}
y} et ∬ D d x d y {\displaystyle \iint _{D}\mathrm {d} x\mathrm {d} y} . Exercice 1-9[modifier | modifier le wikicode] Calculer les intégrales suivantes. ∬ x ≤ 1 , y ≤ 1 , x + y ≥ 1 ( x + y ) d x d y {\displaystyle \iint _{x\leq 1,\;y\leq 1,\;x+y\geq 1}(x+y)\;\mathrm {d} x\;\mathrm {d} y} ; ∬ [ − 1 , 1 ] 2 | x + y | d x d y {\displaystyle \iint
_{[-1,1]^{2}}|x+y|\;\mathrm {d} x\;\mathrm {d} y} ; ∬ D x y d x d y {\displaystyle \iint _{D}xy\;\mathrm {d} x\;\mathrm {d} y} où D {\displaystyle D} est la partie du plan limitée par les paraboles d'équations respectives y = x 2 {\displaystyle y=x^{2}} et x = y 2 {\displaystyle x=y^{2}} ; ∬ x 2 + y 2 ≤ 1 1 1 + x 2 + y 2 d x d y {\displaystyle \iint
_{x^{2}+y^{2}\leq 1}{\frac {1}{1+x^{2}+y^{2}}}\;\mathrm {d} x\;\mathrm {d} y} ; ∬ x ≤ x 2 + y 2 ≤ 1 d x d y ( 1 + x 2 + y 2 ) 2 {\displaystyle \iint _{x\leq x^{2}+y^{2}\leq 1}{\frac {\mathrm {d} x\;\mathrm {d} y}{(1+x^{2}+y^{2})^{2}}}} ; ∬ x 2 a 2 + y 2 b 2 ≤ 1 ( x 2 − y 2 ) d x d y {\displaystyle \iint _{{\frac {x^{2}}{a^{2}}}+
{\frac {y^{2}}{b^{2}}}\leq 1}(x^{2}-y^{2})\;\mathrm {d} x\;\mathrm {d} y} . Exercice 1-10[modifier | modifier le wikicode] Calculer ∫ − a a ( ∫ 0 a 2 − y 2 ( x 2 + y 2 ) 3 / 2 d x ) d y {\displaystyle \int _{-a}^{a}\left(\int _{0}^{\sqrt {a^{2}-y^{2}}}(x^{2}+y^{2})^{3/2}\;\mathrm {d} x\right)\mathrm {d} y} Exercice 1-11[modifier | modifier le
wikicode] Soient 0 < a ≤ b {\displaystyle 0 0 {\displaystyle R>0} , soient D R = { ( x , y ) ∈ ( R + ) 2 ∣ x 2 + y 2 ≤ R 2 } {\displaystyle D_{R}=\{(x,y)\in (\mathbb {R} _{+})^{2}\mid x^{2}+y^{2}\leq R^{2}\}} et K R = [ 0 , R ] 2 {\displaystyle K_{R}=[0,R]^{2}} . Montrer que ∬ D R e − ( x 2 + y 2 ) d x d y ≤ ∬ K R e − ( x 2 + y 2 ) d x d y ≤ ∬ D 2 R
e − ( x 2 + y 2 ) d x d y {\displaystyle \iint _{D_{R}}\operatorname {e} ^{-(x^{2}+y^{2})}\;\mathrm {d} x\;\mathrm {d} y\leq \iint _{K_{R}}\operatorname {e} ^{-(x^{2}+y^{2})}\;\mathrm {d} x\;\mathrm {d} y\leq \iint _{D_{2R}}\operatorname {e} ^{-(x^{2}+y^{2})}\;\mathrm {d} x\;\mathrm {d} y} . En déduire l'existence et la valeur de
lim R → + ∞ ∫ 0 R e − t 2 d t {\displaystyle \lim _{R\to +\infty }\int _{0}^{R}\operatorname {e} ^{-t^{2}}\;\mathrm {d} t} . Recalculer cette intégrale de Gauss J := ∫ 0 + ∞ e − x 2 d x {\displaystyle J:=\int _{0}^{+\infty }\operatorname {e} ^{-x^{2}}\,\mathrm {d} x} en appliquant le théorème de Tonelli à l'application φ : ( x , y ) ↦ x e − x 2 ( 1 +
y 2 ) {\displaystyle \varphi :(x,y)\mapsto x\operatorname {e} ^{-x^{2}(1+y^{2})}} sur D = ] 0 , + ∞ [ 2 {\displaystyle D=\left]0,+\infty \right[^{2}} . Exercice 1-13[modifier | modifier le wikicode] On considère le domaine borné D {\displaystyle D} délimité par les trois droites d'équations x = 0 {\displaystyle x=0} , y = x + 2 {\displaystyle y=x+2}
et y = − x {\displaystyle y=-x} . Calculer ∬ D ( x + y ) d x d y {\displaystyle \iint _{D}\left(x+y\right)\,\mathrm {d} x\mathrm {d} y} : par calcul direct ; en effectuant le changement de variables ( u , v ) = ( x + y , x − y ) {\displaystyle (u,v)=(x+y,x-y)} . Exercice 1-14[modifier | modifier le wikicode] Soient a , b > 0 {\displaystyle a,b>0} . On considère
le domaine D = { ( x , y ) ∈ R + 2 | x 2 a 2 + y 2 b 2 ≤ 1 } {\displaystyle D=\left\{(x,y)\in \mathbb {R} _{+}^{2}~\left|~{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}\leq 1\right.\right\}} (on connaît son aire : π a b / 4 {\displaystyle \pi ab/4} ). Calculer : ∬ D ( 2 x 3 − y ) d x d y {\displaystyle \iint _{D}\left(2x^{3}-y\right)\,\mathrm {d}
x\mathrm {d} y} ; les coordonnées du centre de gravité de D {\displaystyle D} . Exercice 1-15[modifier | modifier le wikicode] L'objet de cet exercice est de calculer l'intégrale ∫ 0 + ∞ sin x x d x {\displaystyle \int _{0}^{+\infty }{\frac {\sin x}{\sqrt {x}}}\,\mathrm {d} x} , dont on sait qu'elle est semi-convergente (Intégration de
Riemann/Exercices/Intégrales impropres#Exercice 5-3). Soit f : R 2 → R , ( x , y ) ↦ e − x y 2 sin x {\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} ,\,(x,y)\mapsto \operatorname {e} ^{-xy^{2}}\sin x} . Montrer que pour tout x > 0 {\displaystyle x>0} , ∫ 0 + ∞ e − x y 2 d y = π 2 x {\displaystyle \int _{0}^{+\infty }\operatorname {e} ^{-
xy^{2}}\,\mathrm {d} y={{\sqrt {\pi }} \over 2{\sqrt {x}}}} (on rappelle que ∫ 0 + ∞ e − t 2 d t = π 2 {\displaystyle \int _{0}^{+\infty }\operatorname {e} ^{-t^{2}}\,\mathrm {d} t={\frac {\sqrt {\pi }}{2}}} : Intégrale de Gauss). En déduire que f {\displaystyle f} n'est pas intégrable sur [ 0 , + ∞ [ 2 {\displaystyle \left[0,+\infty \right[^{2}} .
Montrer que pour tout a > 0 {\displaystyle a>0} , f {\displaystyle f} est intégrable sur [ 0 , a ] × [ 0 , + ∞ [ {\displaystyle [0,a]\times \left[0,+\infty \right[} et en déduire que π 2 ∫ 0 a sin x x d x = ∫ 0 + ∞ g a ( y ) d y , {\displaystyle {{\sqrt {\pi }} \over 2}\int _{0}^{a}{\sin x \over {\sqrt {x}}}\,\mathrm {d} x=\int _{0}^{+\infty }g_{a}(y)\,\mathrm
{d} y,} où g a {\displaystyle g_{a}} est une fonction que l'on déterminera sous forme intégrale. Montrer par une intégration simple que g a ( y ) = 1 − e − a y 2 cos a − y 2 e − a y 2 sin a 1 + y 4 , ∀ y > 0. {\displaystyle g_{a}(y)={1-\operatorname {e} ^{-ay^{2}}\cos a-y^{2}\operatorname {e} ^{-ay^{2}}\sin a \over 1+y^{4}},\ \forall y>0.}
Montrer que ∫ 0 + ∞ g a ( y ) d y {\displaystyle \int _{0}^{+\infty }g_{a}(y)\,\mathrm {d} y} a une limite quand a {\displaystyle a} tend vers + ∞ {\displaystyle +\infty } et calculer cette limite. En admettant que ∫ 0 + ∞ d y 1 + y 4 = π 2 4 {\displaystyle \int _{0}^{+\infty }{\mathrm {d} y \over 1+y^{4}}={\frac {\pi {\sqrt {2}}}{4}}} (Intégration
de Riemann/Exercices/Intégrales impropres#Exercice 5-5), montrer que ∫ 0 + ∞ sin x x d x = π 2 {\displaystyle \int _{0}^{+\infty }{\sin x \over {\sqrt {x}}}\,\mathrm {d} x={\sqrt {\pi \over 2}}} . Exercice 1-16[modifier | modifier le wikicode] Soient f {\displaystyle f} une fonction mesurable sur ] 0 , + ∞ [ {\displaystyle \left]0,+\infty \right[} et
localement intégrable.
On suppose que K := ∫ 0 ∞ f ( x ) x d x {\displaystyle K:=\int _{0}^{\infty }{f(x) \over x}\,\mathrm {d} x} existe et l'on pose F ( x ) = { ∫ [ 1 , x ] f ( t ) d t si x ≥ 1 , ∫ [ x , 1 ] f ( t ) d t si 0 < x < 1. {\displaystyle F(x)={\begin{cases}\int _{[1,x]}f(t)\,\mathrm {d} t&{\text{ si }}x\geq 1,\\\int _{[x,1]}f(t)\,\mathrm {d} t&{\text{ si }}0
Vous aimerez peut-être aussi
- Exercices D'analyse II Notoppo DifficiliDocument43 pagesExercices D'analyse II Notoppo DifficiliSergio Denti100% (1)
- Première Option2022 Equation Réduite DroiteDocument4 pagesPremière Option2022 Equation Réduite DroiteRihana VincentPas encore d'évaluation
- Transformation du radon: Dévoiler des modèles cachés dans les données visuellesD'EverandTransformation du radon: Dévoiler des modèles cachés dans les données visuellesPas encore d'évaluation
- Calcul DifferentielDocument12 pagesCalcul DifferentieldfePas encore d'évaluation
- - Tours de magie expliqués par des bienfaits du calcul littéralD'Everand- Tours de magie expliqués par des bienfaits du calcul littéralPas encore d'évaluation
- Integral Es Double The Ore Me de Fu Bin IDocument10 pagesIntegral Es Double The Ore Me de Fu Bin Ishimirwadanton8Pas encore d'évaluation
- Integrale DoubleDocument13 pagesIntegrale DoubleMarouan DiouriPas encore d'évaluation
- Formule IntegraliDocument1 pageFormule IntegraliAleksaTramošljaninPas encore d'évaluation
- Maaaaath PDFDocument13 pagesMaaaaath PDFMustapha El IdrissiPas encore d'évaluation
- Exercices IntegraleDocument4 pagesExercices IntegralejamesaminePas encore d'évaluation
- MathDocument13 pagesMathnour1960Pas encore d'évaluation
- M32 Chapitre5Document2 pagesM32 Chapitre5Mehda RouPas encore d'évaluation
- td2 Mat 3136 22-23Document3 pagestd2 Mat 3136 22-23STEVE SOBGOUPas encore d'évaluation
- TD Geom S4 2018Document3 pagesTD Geom S4 2018Walter RafaPas encore d'évaluation
- IntegrmultenoDocument4 pagesIntegrmultenoRodrigue patrice Njounhassi koagnePas encore d'évaluation
- Série TD1 Analyse 3Document2 pagesSérie TD1 Analyse 3KIAS DjahidPas encore d'évaluation
- TP05 TTDocument9 pagesTP05 TTAbdelhak DJATOUPas encore d'évaluation
- Rappel MathematiqueDocument1 pageRappel MathematiqueBros LífsinsPas encore d'évaluation
- CasexoDocument529 pagesCasexoandoPas encore d'évaluation
- Aqzsedrftgyhujik, LDocument2 pagesAqzsedrftgyhujik, Labdeljalil mansouriPas encore d'évaluation
- ExamenDocument2 pagesExamenAdel MomoPas encore d'évaluation
- Ex F SolsDocument16 pagesEx F SolsMaxime GGaudetPas encore d'évaluation
- Série TD1 Analyse 3Document2 pagesSérie TD1 Analyse 3djihane.nedjarPas encore d'évaluation
- Série de TD1 - Intégrales Multiples & SolutionsDocument24 pagesSérie de TD1 - Intégrales Multiples & SolutionsAbdelaziz MezianPas encore d'évaluation
- Analyse S2 Chap3Document19 pagesAnalyse S2 Chap3azzamPas encore d'évaluation
- NullDocument1 pageNullZohair RamiPas encore d'évaluation
- Int Multiple PDFDocument4 pagesInt Multiple PDFMichael VincentPas encore d'évaluation
- 04extrait Anal Vectorielle Et Syst DiffDocument7 pages04extrait Anal Vectorielle Et Syst DiffRamzi MansouriPas encore d'évaluation
- Dérivées D'une Fonction Et ExosDocument8 pagesDérivées D'une Fonction Et ExosAntonin DaucimPas encore d'évaluation
- Corrige Chapitre 3Document14 pagesCorrige Chapitre 3Justine DjuikomPas encore d'évaluation
- TD n02 Maths 3 2021 2022Document1 pageTD n02 Maths 3 2021 2022Tom BriderPas encore d'évaluation
- Régression Linéaire MultipleDocument10 pagesRégression Linéaire MultipleChàhiid SimoPas encore d'évaluation
- Intégrales DoublesDocument2 pagesIntégrales Doubleshhindouhindou58Pas encore d'évaluation
- ExOpti CorrectionDocument13 pagesExOpti CorrectionAnthony Christian100% (1)
- Solution - Série 1 (2023-2024)Document6 pagesSolution - Série 1 (2023-2024)mouradzeePas encore d'évaluation
- CH 6 7 EtudDocument58 pagesCH 6 7 EtudDankTehDJY YTPas encore d'évaluation
- Corrige Brevet Polynesie Juin 2021 DVDocument10 pagesCorrige Brevet Polynesie Juin 2021 DVJulien Mi-ShowPas encore d'évaluation
- CP2 Chapitre4Document104 pagesCP2 Chapitre4Yvann FitialalainaPas encore d'évaluation
- TD N°2 Calcul AlgebriqueDocument2 pagesTD N°2 Calcul Algebriquekhadim diagne dPas encore d'évaluation
- Rot Grad DivDocument8 pagesRot Grad DivDominiquePas encore d'évaluation
- 10.TDTP - analyseII FonctionsPlusieursVariablesDocument7 pages10.TDTP - analyseII FonctionsPlusieursVariablesbhb6tzcqfvPas encore d'évaluation
- Logique FR Serie 3 PDFDocument4 pagesLogique FR Serie 3 PDFHassan ElouardiPas encore d'évaluation
- Activites Algebriques Trigonometrie Equations Translation Equations Et Inéquations 2011 2012 (Bellassoued Mohamed)Document4 pagesActivites Algebriques Trigonometrie Equations Translation Equations Et Inéquations 2011 2012 (Bellassoued Mohamed)ajmihnaien96Pas encore d'évaluation
- TD Sur Les IntégralesDocument3 pagesTD Sur Les IntégralesmiguelrikoudomedjoPas encore d'évaluation
- TD 1 Geodiff 2023 2024Document2 pagesTD 1 Geodiff 2023 2024ebenezer n'goranPas encore d'évaluation
- Université de La Réunion/Faculté de Droit Et D'économie L1 Economie, Semestre 2Document5 pagesUniversité de La Réunion/Faculté de Droit Et D'économie L1 Economie, Semestre 2shab.kass4246Pas encore d'évaluation
- L2int td5 MultipleDocument2 pagesL2int td5 MultipleRONICE MAMELEM DJANZEPas encore d'évaluation
- Examen5 Analyse 4 SMA3Document4 pagesExamen5 Analyse 4 SMA3Tizirii AdouamaPas encore d'évaluation
- 1-3 Derivees PartiellesDocument6 pages1-3 Derivees PartiellesMODIBO DEMBÉLÉPas encore d'évaluation
- Fonction GammaDocument2 pagesFonction GammaEssaidi AliPas encore d'évaluation
- LM 256: Travaux Dirig Es - Feuille 2Document6 pagesLM 256: Travaux Dirig Es - Feuille 2Ordinateur Neuf Accessoire CamerounPas encore d'évaluation
- Maths3 Integrales DoublesDocument5 pagesMaths3 Integrales DoublesMeri Mavimar100% (1)
- IntegrationDocument17 pagesIntegrationAidil-Nur ZainalPas encore d'évaluation
- Ex. Parc. 520Document2 pagesEx. Parc. 520Ray MartePas encore d'évaluation
- 1112exam CorrectionDocument4 pages1112exam CorrectionCacchim Kiso0% (1)
- Cours Fonctions - Version ProfDocument11 pagesCours Fonctions - Version Profsoan.soan1230Pas encore d'évaluation
- La Lumière Illus-CouleursDocument52 pagesLa Lumière Illus-Couleurszemarcelo8Pas encore d'évaluation
- Sommaire Codap 2010x Rev 03-11 X Rev10-12Document47 pagesSommaire Codap 2010x Rev 03-11 X Rev10-12Our SalahEddinePas encore d'évaluation
- CI 2020 CorrigéDocument2 pagesCI 2020 Corrigéعبدالرحمان معامريةPas encore d'évaluation
- Cours RDM - MS1 - Partie 1Document53 pagesCours RDM - MS1 - Partie 1gcd19Pas encore d'évaluation
- Ken Wilber - La Physique, Le Mysticisme Et Le Nouveau Paradigme Holographique 1984Document25 pagesKen Wilber - La Physique, Le Mysticisme Et Le Nouveau Paradigme Holographique 1984helabzPas encore d'évaluation
- LE MURMURE DU SERPENT ANCIEN - 26 Mots de Force. Pratiques Secrétés de Sorc PDFDocument14 pagesLE MURMURE DU SERPENT ANCIEN - 26 Mots de Force. Pratiques Secrétés de Sorc PDFBAGAYOKO75% (4)
- Rapport Ecrit 2022 Physique-Chimie PDFDocument3 pagesRapport Ecrit 2022 Physique-Chimie PDFPenda NiassPas encore d'évaluation
- Publier Un StatutDocument5 pagesPublier Un StatutAbdourahmane FayePas encore d'évaluation
- Effort Tranchant PoutreDocument1 pageEffort Tranchant PoutreBec RoudaynaPas encore d'évaluation
- JANAF Termochemical TablesDocument96 pagesJANAF Termochemical TablesAlan Quintanar HaroPas encore d'évaluation
- Exercices Moteur AsynchroneDocument8 pagesExercices Moteur AsynchroneyourparadisPas encore d'évaluation
- TD ELECTROSTATIQUE Serie 2 2022 - 2023Document2 pagesTD ELECTROSTATIQUE Serie 2 2022 - 2023miguelrikoudomedjoPas encore d'évaluation
- Méthode Des Différences Finies Pour Les EDP Évolution PDFDocument11 pagesMéthode Des Différences Finies Pour Les EDP Évolution PDFAzize Razam100% (1)
- Légende HiramDocument4 pagesLégende HiramRosa_Tur_9524100% (2)
- Cours Automate Scheinder TSX2-2-2Document12 pagesCours Automate Scheinder TSX2-2-2Eliance GrahoPas encore d'évaluation
- Rapport FinaleDocument162 pagesRapport FinaleArij Naily Ep HammamiPas encore d'évaluation
- Rapport de Travaux Pratiques de Mécanique Des Sols - Groupe 1 - Sous Groupe 1 PDFDocument34 pagesRapport de Travaux Pratiques de Mécanique Des Sols - Groupe 1 - Sous Groupe 1 PDFOumarPas encore d'évaluation
- Optique GeoDocument58 pagesOptique GeoYassineZkl100% (1)
- Capteur de ForceDocument5 pagesCapteur de ForceNéjib M'hiriPas encore d'évaluation
- BACCons Mécaniquedesfluides Exercices CH 2Document3 pagesBACCons Mécaniquedesfluides Exercices CH 2fatihamPas encore d'évaluation
- Nouveau Document Microsoft WordDocument10 pagesNouveau Document Microsoft WordxlxlxlxlPas encore d'évaluation
- Atf 45-3Document15 pagesAtf 45-3ragkaraPas encore d'évaluation
- Tour R+9Document134 pagesTour R+9RÊDÄ ÜhPas encore d'évaluation
- CCP - MP - 2007 - CorrigeDocument7 pagesCCP - MP - 2007 - Corrigejazzzy0517% (6)
- Thermo 3Document4 pagesThermo 3lilian01.larochePas encore d'évaluation
- Exercices Fonctions Affines-1Document7 pagesExercices Fonctions Affines-1Bartholomé THURPas encore d'évaluation
- PanelsDocument7 pagesPanelsalioua aliPas encore d'évaluation
- Majeur2 PhotodetectionDocument62 pagesMajeur2 PhotodetectionIheb HamedPas encore d'évaluation
- Aprue 10Document8 pagesAprue 10Ariel Angelo ElegbedePas encore d'évaluation
- EMD S1 CM 2023 M2 CM (Récupération Automatique)Document3 pagesEMD S1 CM 2023 M2 CM (Récupération Automatique)nawel mezighechePas encore d'évaluation
- Théorie relative de la musique: Maîtriser le mouvement par la logique des intervallesD'EverandThéorie relative de la musique: Maîtriser le mouvement par la logique des intervallesÉvaluation : 4 sur 5 étoiles4/5 (1)
- L'Ombre à l'Univers: La structure des particules élémentaires XIIfD'EverandL'Ombre à l'Univers: La structure des particules élémentaires XIIfPas encore d'évaluation
- Électrotechnique | Pas à Pas: Bases, composants & circuits expliqués pour les débutantsD'EverandÉlectrotechnique | Pas à Pas: Bases, composants & circuits expliqués pour les débutantsÉvaluation : 5 sur 5 étoiles5/5 (1)
- Physique quantique pour les débutants: Découvrez les fondements de la mécanique quantique et la façon dont elle affecte le monde dans lequel nous vivons à travers ses théories les plus célèbresD'EverandPhysique quantique pour les débutants: Découvrez les fondements de la mécanique quantique et la façon dont elle affecte le monde dans lequel nous vivons à travers ses théories les plus célèbresÉvaluation : 5 sur 5 étoiles5/5 (2)
- Les LES TRUCS MATHEMATIQUES AU PRIMAIRE: et si on leur donnait du sens!D'EverandLes LES TRUCS MATHEMATIQUES AU PRIMAIRE: et si on leur donnait du sens!Évaluation : 2 sur 5 étoiles2/5 (1)
- La pensée dirigée: Traité sur le raisonnement et les logiquesD'EverandLa pensée dirigée: Traité sur le raisonnement et les logiquesÉvaluation : 5 sur 5 étoiles5/5 (2)
- Mathématiques et Mathématiciens Pensées et CuriositésD'EverandMathématiques et Mathématiciens Pensées et CuriositésÉvaluation : 4.5 sur 5 étoiles4.5/5 (5)
- L'univers est intelligent. L'âme existe. Mystères quantiques, multivers, intrication, synchronicité. Au-delà de la matérialité, pour une vision spirituelle du cosmos.D'EverandL'univers est intelligent. L'âme existe. Mystères quantiques, multivers, intrication, synchronicité. Au-delà de la matérialité, pour une vision spirituelle du cosmos.Pas encore d'évaluation
- Enjeux contemporains de l'éducation scientifique et technologiqueD'EverandEnjeux contemporains de l'éducation scientifique et technologiqueAbdelkrim HasniPas encore d'évaluation
- Sur les fondements de la théorie des ensembles transfinisD'EverandSur les fondements de la théorie des ensembles transfinisPas encore d'évaluation
- Historique et description des procédés du daguerréotype et du diorama: Essai historique sur les sciences et techniquesD'EverandHistorique et description des procédés du daguerréotype et du diorama: Essai historique sur les sciences et techniquesPas encore d'évaluation
- Voyager à Travers les Mondes Parallèles pour Atteindre vos RêvesD'EverandVoyager à Travers les Mondes Parallèles pour Atteindre vos RêvesÉvaluation : 4 sur 5 étoiles4/5 (11)
- Saturne: Les Grands Articles d'UniversalisD'EverandSaturne: Les Grands Articles d'UniversalisPas encore d'évaluation
- Signe pour le Saint Graal? Énergie infinie avec des possibilités infinies! Mesurer avec l’antenne de Lecher à Carnac et en Bretagne en FranceD'EverandSigne pour le Saint Graal? Énergie infinie avec des possibilités infinies! Mesurer avec l’antenne de Lecher à Carnac et en Bretagne en FrancePas encore d'évaluation
- Le must bilingue™ du lycéen Vol. 2 - les maths en anglaisD'EverandLe must bilingue™ du lycéen Vol. 2 - les maths en anglaisPas encore d'évaluation
- Guide complet de la Numérologie: Édition 30e anniversaireD'EverandGuide complet de la Numérologie: Édition 30e anniversaireÉvaluation : 4 sur 5 étoiles4/5 (1)
- Je me prépare aux examens du ministère en mathématiques: Es-tu prêt à passer le test ?D'EverandJe me prépare aux examens du ministère en mathématiques: Es-tu prêt à passer le test ?Évaluation : 4 sur 5 étoiles4/5 (1)
- Detection des collisions dans les jeux video 2D: avec C#5, WPF et Visual Studio 2013D'EverandDetection des collisions dans les jeux video 2D: avec C#5, WPF et Visual Studio 2013Pas encore d'évaluation
- Exercices d'optique et d'électromagnétismeD'EverandExercices d'optique et d'électromagnétismeÉvaluation : 5 sur 5 étoiles5/5 (1)