Cours Vom Djelouah PDF

V
V
V
I
I
I
B
B
B
R
R
R
A
A
A
T
T
T
I
I
I
O
O
O
N
N
N
S
S
S

E
E
E
T
T
T

O
O
O
N
N
N
D
D
D
E
E
E
S
S
S

M
M
M
E
E
E
C
C
C
A
A
A
N
N
N
I
I
I
Q
Q
Q
U
U
U
E
E
E
S
S
S

Universit des Sciences et de la Technologie
Houari Boumediene

Facult de Physique
C
C
C
o
o
o
u
u
u
r
r
r
s
s
s

&
&
&

E
E
E
x
x
x
e
e
e
r
r
r
c
c
c
i
i
i
c
c
c
e
e
e
s
s
s

D
D
D
e
e
e
u
u
u
x
x
x
i
i
i
m
m
m
e
e
e

A
A
A
n
n
n
n
n
n
e
e
e

d
d
d
e
e
e
s
s
s

F
F
F
i
i
i
l
l
l
i
i
i
r
r
r
e
e
e
s
s
s

S
S
S
c
c
c
i
i
i
e
e
e
n
n
n
t
t
t
i
i
i
f
f
f
i
i
i
q
q
q
u
u
u
e
e
e
s
s
s

d
d
d
e
e
e
s
s
s

U
U
U
n
n
n
i
i
i
v
v
v
e
e
e
r
r
r
s
s
s
i
i
i
t
t
t
s
s
s

e
e
e
t
t
t

d
d
d
e
e
e
s
s
s

E
E
E
c
c
c
o
o
o
l
l
l
e
e
e
s
s
s

d
d
d
I
I
I
n
n
n
g
g
g
n
n
n
i
i
i
e
e
e
u
u
u
r
r
r
s
s
s

Anne Universitaire 2011-2012
Pr. DJELOUAH Hakim
Universit des Sciences et de la Technologie Houari Boumediene
Facult de Physique
Licence de Physique - L2 - S3
Module : Physique 3
Vibrations et Ondes Mcaniques
Cours & Exercices
H. Djelouah
Anne Universitaire 2011-2012
ii
Avant-Propos
Au sujet de ce manuel
Ce manuel a t crit lintention des tudiants de deuxime anne des lires scientiques et
techniques des universits et coles dingnieurs dAlgrie. Il correspond au programme ociel
du module Vibrations et Ondes mcaniques enseign en deuxime anne (L2-S3) des lires
ST-Sciences et Technique et SM-Sciences de la Matire.
Les objectifs assigns par ce programme portent sur linitiation des tudiants de deuxime
anne aux phnomnes de vibrations mcaniques et de propagation des ondes mcaniques. Ce
manuel essaie de rpondre au mieux aux recommandations du programme ociel.
Lutilisation du formalisme de Lagrange est clairement spcie dans le programme ociel.
Nous avons essay dintroduire le formalisme de Lagrange le plus simplement possible dans le
cas particulier dun systme une particule possdant un degr de libert. La classication
des dirents types de liaison nest pas aborde. Il nous a sembl opportun dinsister sur la
notion de force gnralise et dintroduire, dans le cas des systmes dissipatifs, la notion de
fonction dissipation. La gnralisation aux systmes plusieurs degrs de libert est nonce
sans dmonstration.
Ltude des oscillations est volontairement restreinte aux oscillations de faible amplitude.
Cette dmarche est prsente dans le chapitre intitul Oscillations libres des systmes un
degr de libert. De plus, les seules forces de frottement prises en comptes sont les forces de
frottement de viscosit proportionnelles la vitesse.
Les notions de rsonance et dimpdance mcanique font lobjet du chapitre suivant consacr
aux oscillations forces des systmes un degr de libert. Ltude des systmes oscillatoires
plusieurs degrs de libert est restreinte aux systmes possdant deux degrs de libert. La
mthode matricielle de recherche des modes nest pas utilise en raison des connaissances pr-
requises en calcul matriciel. Nous avons opt pour une dmarche base sur la superposition de
solutions particulires sinusodales. Ltude des oscillations forces des systmes deux degrs de
libert permet de consolider les notions de rsonance et dimpdance et dintroduire le phnomne
danti-rsonance. Les analogies entre les systmes lectriques et mcaniques sont prsentes dans
une annexe.
Le programme ociel recommande dintroduire la propagation des ondes mcaniques en
utilisant le modle de la chane linaire et assurer ensuite le passage du milieu discret au milieu
continu; nous avons estim que cette dmarche, bien que trs intressante, ntait pas adapte
au niveau de nos tudiants car elle introduit la notion donde par des concepts relativement
diciles tels que la notion de dispersion. Pour cela nous avons prfr introduire la propagation
des ondes mcaniques travers le modle plus classique de la corde vibrante qui permet de mettre
en vidence la dirence entre vitesse de vibration et vitesse de propagation. Pour des raisons
pdagogiques, nous avons prfr tablir lquation de propagation laide du formalisme de
Newton plutt quen utilisant le formalisme de Lagrange. Lquation de propagation est rsolue
par la mthode de dAlembert prsente dans un chapitre intitul Gnralits sur les phnomnes
de propagation. La mthode de Fourier est prsente lors de la rsolution du problme des
oscillations libres dune corde de longueur nie. Les notions dimpdance, de modes propres et
de rsonance sont dnies dans ce chapitre.
La propagation des ondes lastiques dans les solides est aborde dans le chapitre suivant
o, volontairement, nous avons prfr commencer par les systmes continus non dispersifs puis
aborder le modle de la chane linaire et nir avec le passage la limite dun milieu discret vers
un milieu continu.
La propagation des ondes acoustiques dans les uides est aborde dans le dernier chapitre.
Les notions dintensit acoustique et de niveau sonore sont prsentes dans des cas simples.
Leet Doppler est introduit de faon assez sommaire.
H. Djelouah
iii
Semaine Cours Travaux Dirigs
1 Equations direntielles Rappels de mcanique
2 Formalisme de Lagrange Equations direntielles
3 Oscillations libres des sys-
tmes non amortis 1 degr
de libert
Formalisme de Lagrange
tmes amortis 1 degr de li-
bert
Oscillations libres des sys-
tmes non amortis 1 degr
de libert
5 Oscillations forces des sys-
tmes un degr de libert
tmes amortis 1 degr de li-
bert
tmes deux degr de libert
Oscillations forces des sys-
tmes un degr de libert
7 Oscillations forces des sys-
tmes deux degrs de libert
tmes deux degr de libert
8 Gnralits sur les ondes Oscillations forces des sys-
tmes deux degrs de libert
9 Cordes vibrantes Gnralits sur les ondes
10 Ondes acoustiques dans les
uides
Cordes vibrantes
11 Ondes dans les milieux dis-
crets
Ondes acoustiques dans les
uides
12 Ondes lastiques dans les so-
lides
Ondes dans les milieux dis-
crets
Table 1: Proposition de progression des enseignements
An de combler les lacunes ventuelles des tudiants venant de premire anne, il nous a
sembl ncessaire de consacrer un chapitre entier (Annexe) la rsolution des quations di-
rentielles du second ordre coecients constants.
Enn, une bibliographie sommaire prsente les principaux ouvrages utiliss pour la confection
de ce manuel.
Gestion du temps pdagogique
Le contenu de ce programme est prvu pour tre enseign pendant un semestre de 15 se-
maines, raison de deux cours hebdomadaires de 1h30mn et une sance de travaux dirigs
de 1h30mn par semaine. Toutefois pour diverses raisons, la dure relle de lenseignement par
semestre est de 12-13 semaines. An de couvrir la plus grande partie du programme ociel
pendant cette dure une gestion rigoureuse du temps pdagogique ainsi quune coordination-
synchronisation entre les cours et les travaux dirigs sont indispensables. Nous recommandons
la progression ci-dessus (Tableau 1) dans laquelle la dure relle du semestre (12-13 semaines)
est rpartie quitablement entre les vibrations mcaniques et les ondes mcaniques.
Ce manuel est le fruit dune longue pratique pdagogique dans cette matire et rsulte
de longues discussions avec les collgues qui ont eu assurer cet enseignement. Les exercices
proposs dans ce manuel ont t confectionns partir dune compilation des sries dexercices
et des sujets dexamens proposs par les collgues qui enseignent le module Vibrations et Ondes
Mcaniques la Facult de Physique de lUniversit des Sciences et de la Technologie Houari
Boumediene.
H. Djelouah
iv
En parallle un enseignement de travaux pratiques est dispens dans un autre module
raison dune sance de 3 heures toutes les deux semaines. Les collgues en charge du module
de travaux pratiques essaient de synchroniser le contenu de leur enseignement avec le contenu
dispens en cours et en travaux dirigs.
H. Djelouah
Table des matires
Avant-Propos ii
1 Introduction aux quations de Lagrange 1
1.1 Equations de Lagrange pour une particule . . . . . . . . . . . . . . . . . . . . . . 1
1.1.1 Equations de Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.2 Cas des systmes conservatifs . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1.3 Cas des forces de frottement dpendant de la vitesse . . . . . . . . . . . . 3
1.1.4 Cas dune force extrieure dpendant du temps . . . . . . . . . . . . . . . 5
1.2 Systme plusieurs degrs de libert . . . . . . . . . . . . . . . . . . . . . . . . . 5
2 Oscillations libres des systmes un degr de libert 7
2.1 Oscillations non amorties . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1.1 Oscillateur linaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1.2 Energie cintique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1.3 Energie potentielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.1.4 Equation direntielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.1.5 Rsolution de lquation direntielle de loscillateur harmonique simple . 8
2.2 Oscillations libres des systmes amortis un degr de libert . . . . . . . . . . . 9
2.2.1 Equation de Lagrange pour les systmes dissipatifs . . . . . . . . . . . . . 9
2.2.2 Cas particulier des oscillations de faible amplitude . . . . . . . . . . . . . 9
2.2.3 Rsolution de lquation direntielle . . . . . . . . . . . . . . . . . . . . . 10
3 Oscillations forces des systmes un degr de libert 17
3.1 Equation direntielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.2 Systme masse-ressort-amortisseur . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.3 Solution de lquation direntielle . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.3.1 Cas particulier o A(t) = A
0
cos(t) . . . . . . . . . . . . . . . . . . . . . 19
3.3.2 Cas dune excitation priodique . . . . . . . . . . . . . . . . . . . . . . . . 22
3.4 Impdance mcanique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3.4.1 Dnition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3.4.2 Impdances mcaniques . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3.4.3 Puissance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3.4.4 Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
4 Oscillations libres des systmes deux degrs de libert 29
4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
4.2 Systmes deux degrs de libert . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
4.2.1 Systme masses-ressorts en translation . . . . . . . . . . . . . . . . . . . . 30
4.2.2 Cas particulier de deux oscillateurs identiques . . . . . . . . . . . . . . . . 33
4.2.3 Pendules coupls . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
H. Djelouah
vi TABLE DES MATIRES
5 Oscillations forces des systmes deux degrs de libert 41
5.1 Equations de Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
5.2 Systme masses-ressorts-amortisseurs . . . . . . . . . . . . . . . . . . . . . . . . . 41
5.2.1 Equations direntielles . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
5.2.2 Etude du rgime permanent sinusodal . . . . . . . . . . . . . . . . . . . . 42
5.3 Impdance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
5.4 Application . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
6 Gnralits sur les phnomnes de propagation 47
6.1 Propagation une dimension . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
6.1.1 Equation de propagation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
6.1.2 Solution de lquation de propagation . . . . . . . . . . . . . . . . . . . . 47
6.1.3 Onde progressive sinusodale . . . . . . . . . . . . . . . . . . . . . . . . . 50
6.1.4 Superposition de deux ondes progressives sinusodales . . . . . . . . . . . 51
6.1.5 Vitesse de phase . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
6.1.6 Vitesse de groupe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
6.1.7 Onde vectorielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
6.2 Propagation dans lespace trois dimensions . . . . . . . . . . . . . . . . . . . . 55
6.2.2 Onde plane progressive sinusodale . . . . . . . . . . . . . . . . . . . . . . 55
7 Cordes vibrantes 59
7.1 Equation des ondes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
7.2 Ondes progressives harmoniques . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
7.2.1 Dnition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
7.2.2 Force en un point . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
7.2.3 Impdance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
7.3 Oscillations libres dune corde de longueur nie . . . . . . . . . . . . . . . . . . . 61
7.4 Rexion et transmission . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
7.4.1 Rexion et transmission entre deux cordes semi-innies . . . . . . . . . . 63
7.4.2 Rexion sur une impdance quelconque . . . . . . . . . . . . . . . . . . . 63
8 Ondes lastiques dans les solides 67
8.1 Proprits lastiques des solides . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
8.1.1 Dformation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
8.1.2 Contrainte moyenne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
8.1.3 Loi de Hooke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
8.1.4 Coecient de Poisson . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
8.1.5 Loi de Hooke pour les forces tangentielles . . . . . . . . . . . . . . . . . . 69
8.2 Onde plane longitudinale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
8.2.2 Ondes progressives harmoniques . . . . . . . . . . . . . . . . . . . . . . . 70
8.2.3 Rexion et transmission . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
8.2.4 Oscillations libres dun barreau . . . . . . . . . . . . . . . . . . . . . . . . 72
8.2.5 Oscillations forces dun barreau de longueur nie . . . . . . . . . . . . . 74
8.3 Ondes lastiques transversales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
8.4 Modle de la chane linaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
8.4.1 Modlisation microscopique du problme et mise en quations. . . . . . . 76
8.4.2 Solution en rgime permanent sinusodal . . . . . . . . . . . . . . . . . . . 77
8.4.3 Lapproximation dun milieu continu. . . . . . . . . . . . . . . . . . . . . 78
H. Djelouah
TABLE DES MATIRES vii
9 Ondes acoustiques dans les uides 83
9.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
9.2 Equation donde . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
9.3 Vitesse du son . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
9.4 Onde progressive sinusodale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
9.4.1 Dnition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
9.4.2 Impdance acoustique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
9.4.3 Energie acoustique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
9.5 Rexion-Transmission . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
9.6 Eet Doppler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
9.6.1 Dnition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
9.6.2 Cas particulier des faibles vitesses . . . . . . . . . . . . . . . . . . . . . . 92
A Equations direntielles 95
A.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
A.2 Equation homogne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
A.2.1 Rgime fortement amorti ( >
0
) . . . . . . . . . . . . . . . . . . . . . 96
A.2.2 Rgime critique ( =
O
) . . . . . . . . . . . . . . . . . . . . . . . . . . 97
A.2.3 Rgime pseudo-priodique ( <
0
) . . . . . . . . . . . . . . . . . . . . 97
A.3 Equation avec second membre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
A.3.1 Solution gnrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
A.3.2 Cas particulier o A(t) est constante . . . . . . . . . . . . . . . . . . . . . 100
A.3.3 Cas particulier o A(t) = A
0
cos(t) : . . . . . . . . . . . . . . . . . . . . 101
A.3.4 Cas o A(t) est une fonction priodique du temps . . . . . . . . . . . . . 102
B Analogies lectromcaniques 107
B.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
B.2 Analogie force-tension ou masse-inductance . . . . . . . . . . . . . . . . . . . . . 107
B.3 Systmes un degr de libert . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
B.4 Systme deux degrs de libert . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
Bibliographie 112
H. Djelouah
viii TABLE DES MATIRES
H. Djelouah
Chapitre 1
Introduction aux quations de
Lagrange
1.1 Equations de Lagrange pour une particule
1.1.1 Equations de Lagrange
Considrons le cas particulier dune particule astreinte se dplacer, sans frottement, sur
une courbe plane contenue dans le plan xOy. La courbe sur laquelle est astreinte se dplacer
la particule de masse m, est le lieu des points dont les coordonnes vrient les relations :
_
z = 0
f(x, y) = 0
La premire relation correspond au plan xOy . La seconde relation reprsente lquation de la
trajectoire dans ce plan. Ces deux relations dnissent les quations des liaisons appeles souvent
liaisons. Le nombre de degrs de libert est gal au nombre de coordonnes qui reprsentent la
position de m (trois dans le cas gnral) moins le nombre de liaisons (deux dans le cas particulier
tudi ici). La particule possde donc un degr de libert. Il faut choisir une variable q pour
reprer sa position. Cette variable est appele coordonne gnralise. Il est possible dexprimer
le vecteur position r de la particule en fonction de la coordonne gnralise q par la relation :
r = r (q).
Soit

F la rsultante de toutes les forces agissant sur la particule. La relation fondamentale
de la dynamique scrit :
F = m
d
2
r
dt
2
= m
dv
dt
o v =
dr
dt
est la vitesse de la particule.
Soit W le travail fourni par la force

F lors dun dplacement innitsimal r :
W =

F r
Le dplacement innitsimal r peut scrire en fonction de la variation q de la coordonne
gnralise q :
r =
r
q
q
Dans ce cas le travail W peut se mettre la forme :
H. Djelouah
2 Introduction aux quations de Lagrange
W =

F
r
q
q
On appelle force gnralise conjugue de q, ou q-composante de la force, la quantit F
q
dnie par :
F
q
=
W
q
=

F
r
q
Par consquent W scrit :
W = F
q
q
En tenant compte de la relation fondamentale de la dynamique, cette expression peut ga-
lement scrire :
W = m
dv
dt

r
q
q
Dautre part :
d
dt
_
v
r
q
_
=
dv
dt

r
q
+v
d
dt
_
r
q
_
Sachant que
d
dt
_
r
q
_
=

q
_
dr
dt
_
=
v
q
on obtient
dv
dt

r
q
=
d
dt
_
v
r
q
_
v
v
q
Le vecteur vitesse v, peut aussi scrire :
v =
dr
dt
=
r
q
q
t
=
r
q
q
Do la relation :
r
q
=
v
q
et
dv
dt

r
q
=
d
dt
_
v
v
q
_
v
v
q
Sachant que
q
_
1
2
v
2
_
=

q
_
1
2
v v
_
= v
v
q
et que
q
_
1
2
v
2
_
=

q
_
1
2
v v
_
= v
v
q
on obtient
dv
dt

r
q
=
d
dt
_

q
_
1
2
v
2
__

q
_
1
2
v
2
_
Lexpression du travail W peut alors scrire :
H. Djelouah
1.1 Equations de Lagrange pour une particule 3
W = m
_
d
dt
_

q
_
1
2
v
2
__

q
_
1
2
v
2
__
q
Si on note T =
1
2
mv
2
lnergie cintique de la masse m , on obtient nalement :
W =
_
d
dt
_
T
q
_
T
q
_
q
On obtient nalement les deux expressions quivalentes du travail W
_
d
dt
_
T
q
_
T
q
_
q = F
q
q
On en dduit lquation de dAlembert pour un systme un degr de libert :
d
dt
_
T
q
_
T
q
= F
q
1.1.2 Cas des systmes conservatifs
Dans les systmes conservatifs, la force applique au systme drive dun potentiel U et elle
scrit :
F
q
=
U
q
Lquation de Lagrange devient alors :
d
dt
_
T
q
_
T
q
=
U
q
Gnralement lnergie potentielle U ne dpend pas de la vitesse, cestdire que
U
q
= 0.
Lquation de Lagrange peut alors scrire :
d
dt
_
(T U)
q
_
(T U)
q
= 0
On introduit la fonction de Lagrange ( ou lagrangien du systme ) qui est la dirence de
lnergie cintique et de lnergie potentielle :
L = T U
Do la forme de lquation de Lagrange dans le cas dun systme conservatif :
d
dt
_
L
q
_
L
q
= 0
1.1.3 Cas des forces de frottement dpendant de la vitesse
Equation de Lagrange
Considrons une situation physique dans laquelle la particule est soumise des forces de
frottement de viscosit dont la rsultante

f est de la forme :
f = v
Pour calculer la force gnralise f
q
correspondante, nous utilisons la dnition du paragraphe
prcdent :
H. Djelouah
f
q
=

f
r
q
=
_
r
q
_
2
q
t
Cette dernire expression peut se mettre sous la forme :
f
q
= q
avec
=
_
r
q
_
2
Si en plus des forces qui drivent dun potentiel il existe des forces de frottement de viscosit,
lquation de Lagrange scrit :
d
dt
_
T
q
_
T
q
= F
U,q
+f
q
o F
U,q
=
U
q
reprsente les forces qui drivent dun potentiel. Do :
d
dt
_
L
q
_
L
q
= q
Fonction dissipation
Calculons le travail W
f
fourni par la force de frottement pendant un intervalle de temps t
pour un dplacement r :
W
f
=

f r = v
2
t
La quantit de chaleur Q gagne par le systme en interaction avec la particule, est telle
que :
Q = v
2
t
Soit P
d
=
Q
t
la puissance dissipe par les forces de frottement sous forme de chaleur :
P
d
= v
2
Cette puissance dissipe peut tre exprime en fonction de q, par :
P
d
=
_
dr
dt
_
2
=
_
r
q
q
t
_
2
= q
2
Par dnition, la fonction dissipation est gale la demi-puissance dissipe :
T =
1
2
P
d
=
1
2
q
2
La q-composante f
q
de la force de frottement peut alors scrire :
f
q
=
T
q
Lquation de Lagrange scrit alors :
d
dt
_
L
q
_
L
q
+
T
q
= 0
H. Djelouah
1.2 Systme plusieurs degrs de libert 5
1.1.4 Cas dune force extrieure dpendant du temps
Considrons le cas plus gnral dune force extrieure dpendant du temps agissant sur un
systme qui est le sige de forces de frottement qui drivent dune fonction dissipation T. Soit
F
eq
la q-composante de la force extrieure. Dans ce cas lquation de Lagrange peut scrire sous
lune des deux formes quivalentes suivantes :
d
dt
_
L
q
_
L
q
= F
eq
q
d
dt
_
L
q
_
L
q
+
T
q
= F
e,q
1.2 Systme plusieurs degrs de libert
Dans le cas gnral dun systme plusieurs degrs de libert, il y a autant dquations
de Lagrange que de degrs de libert. Ainsi, si le systme possde N degrs de libert, il est
ncessaire davoir N coordonnes gnralises q
i
(i = 1, 2, ...., N) ; nous aurons ainsi N quations
de Lagrange :
d
dt
_
L
q
i
_
L
q
i
+
T
q
i
= F
e,q
i
(i = 1, 2, ...., N)
La q
i
composante de la force gnralise extrieure est dnie par :
F
e,q
i
=
W
q
i
q
i
=0
Dans cette expression W reprsente le travail des forces extrieures rsultant dune variation
q
i
de la coordonne q
i
telle que les coordonnes q
j=i
soient constantes (q
j=i
= 0).
Exercices
Exercice 1 : On considre un point matriel astreint se dplacer sur un cercle de rayon R et
de centre O contenu dans le plan xOy.
1. Traduire la liaison par une ou des relations mathmatiques ; quel est le nombre de degrs
de libert de ce point ?
2. Quelles sont les coordonnes gnralises que lon peut utiliser pour reprer ce point ?
Exercice 2 : On considre un point matriel astreint se dplacer sur une sphre. Rpondre
aux mmes questions que lexercice prcdent.
Exercice 3 : Pour reprer la position dun solide dans lespace, il faut reprer la position de
trois points non aligns A, B et C de ce solide.
1. Traduire les liaisons physiques par des relations mathmatiques ; quel est le nombre de
degrs de libert de ce solide ?
2. Quelles sont les coordonnes gnralises les plus couramment utilises pour dcrire le
mouvement dun solide ?
3. Quel est le nombre de degrs de libert pour un solide qui possde :
(a) un point xe ?
(b) deux points xes ?
H. Djelouah
Exercice 4 : On considre une haltre constitue de deux masses identiques m, supposes
ponctuelles, relies par une tige de longueur a, de diamtre et de masse ngligeables.
1. Comment scrit mathmatiquement la liaison entre les deux masses ?
2. Quel est le nombre de degrs de libert de ce systme ?
Exercice 5 : On considre une masse M qui glisse sans frottement selon une droite sur un
plan horizontal. Elle est relie un bti xe par un ressort parfait de raideur k, colinaire avec
la trajectoire.
1. Quel est le nombre de degrs de libert ?
2. Quelles sont les forces qui sexercent sur la masse M. Quelles sont celles qui drivent dun
potentiel ? Quelles sont celles qui ne travaillent pas ?
3. Calculer lnergie cintique et lnergie potentielle de ce systme ; en dduire lquation
direntielle du mouvement par la mthode des quations de Lagrange.
4. Etablir lquation direntielle du mouvement en utilisant la seconde loi de Newton; que
remarque-t-on? Quelles sont les forces qui ninterviennent pas dans lquation de Lagrange
et qui sont prises en compte dans les quations de Newton? Quelle est leur particularit ?
Exercice 6 : On considre un pendule simple constitu dune masse m relie un point xe
O par un l de longueur et de masse ngligeable. Cette masse peut osciller librement dans le
plan vertical xOy.
1. Quel est le nombre de degrs de libert de ce systme ? Quelles sont les coordonnes
gnralises les plus pratiques utiliser ? Ecrire les coordonnes x et y de la masse m dans
le repre xOy en fonction des coordonnes gnralises choisies.
2. Quelles sont les forces qui sexercent sur la masse m. Quelles sont celles qui drivent dun
potentiel ? Quelles sont celles dont le travail nest pas nul au cours du mouvement ?
3. Etablir les quations du mouvement par la mthode des quations de Lagrange.
4. Ecrire les quations du mouvement par la mthode de Newton; retrouve-t-on le mme
rsultat que par la mthode de Lagrange ? Dterminer le module de laction du l sur la
masse m; pouvait-on dterminer ce module par la mthode de Lagrange ? Commenter le
rsultat.
Exercice 7 : Etudier le mouvement dun cylindre de masse M et de rayon R, qui roule
sans glisser le long de la ligne de plus grande pente dun plan inclin qui fait un angle avec
lhorizontale.
Exercice 8 : Etudier laide des quations de Lagrange, le mouvement dune masse M qui
glisse sur un plan inclin faisant un angle avec lhorizontale, avec un coecient de frottement
de glissement . La masse est soumise de plus une force F(t) parallle au plan inclin.
Exercice 9 : Etudier, laide des quations de Lagrange, le mouvement dun cylindre de masse
M et de rayon R autour de son axe de rvolution x horizontalement, entran en rotation par
laction de forces extrieures dont le moment par rapport laxe de rotation est /(t).
Exercice 10 : Une particule de masse m est lche sans vitesse initiale dans un uide caractris
par un coecient de frottement visqueux . Etudier son mouvement laide des quations de
Lagrange.
Exercice 11 : Etablir lquation direntielle du mouvement, dans un plan vertical, dune
masse ponctuelle m relie un point O par une tige de longueur et de masse ngligeable. La
masse est soumise une force F(t) qui reste perpendiculaire la tige lors du mouvement. Les
forces de frottement de viscosit peuvent tre ramenes une force

f = v applique la
masse m dont la vitesse instantane est v . Le coecient de frottement visqueux est suppos
constant.
H. Djelouah
Chapitre 2
Oscillations libres des systmes un
degr de libert
2.1 Oscillations non amorties
2.1.1 Oscillateur linaire
Un systme oscillant un degr de libert est habituellement repr laide dune coordonne
gnralise q qui est lcart par rapport la position dquilibre stable. Le mouvement vibratoire
est dit linaire sil est rgi par une quation direntielle harmonique de la forme :
q +
2
0
q = 0
Cette quation est appele quation direntielle de loscillateur harmonique simple.
2.1.2 Energie cintique
Dans le cas dun systme un degr de libert, constitu dune masse m dont la position est
repre par la coordonne gnralise q, lnergie cintique scrit :
T =
1
2
mv
2
=
1
2
m
_
r
t
_
2
=
1
2
m
_
r
q
q
t
_
2
=
1
2
m
_
r
q
_
2
q
2
Lnergie cintique dun systme un degr de libert est fonction de q et q . Elle peut
scrire sous la forme :
T =
1
2
a(q) q
2
o a(q) est une fonction de la coordonne gnralise q, dnie dans le cas tudi par :
a(q) = m
_
r
q
_
2
En faisant un dveloppement limit de a(q) au second ordre en q, au voisinage de q = 0 , on
obtient :
T(q, q) =
1
2
_
_
a(0) +
a
q
q=0
q +
1
2
2
a
q
2
q=0
q
2
+
_
_
q
2
En limitant lapproximation au second ordre, on obtient :
T =
1
2
a
0
q
2
o a
0
est une constante gale a (0) .
H. Djelouah
8 Oscillations libres des systmes un degr de libert
2.1.3 Energie potentielle
Les oscillations se font autour de la position dquilibre stable q = 0 caractrise par :
U
q
q=0
= 0
Il est toujours possible , lorsque les carts par rapport la position dquilibre sont faibles, de
faire un dveloppement en srie de Taylor de U(q) au voisinage de la position dquilibre q = 0.
En ngligeant les puissances de q dordre suprieur deux, on obtient :
U(q) = U(0) +
U
q
q=0
q +
1
2
2
U
q
2
q=0
q
2
+
q = 0 correspond un minimum de U(q) pour lequel
U
q
q=0
= 0 et

2
U
q
2
q=0
> 0
Si on choisit lorigine de lnergie potentielle cette position dquilibre (U(0) = 0) , lnergie
potentielle U (q) peut scrire sous une forme quadratique :
U(q)
1
2
b
0
q
2
avec : b
0
=

2
U
q
2
q=0
2.1.4 Equation direntielle
Lquation de Lagrange scrit :
d
dt
_
L
q
_
L
q
= 0
Ce qui permet dobtenir lquation direntielle de loscillateur harmonique simple avec la
valeur de la pulsation propre
0
:
2
0
=
b
0
a
0
=
2
U
q
2
q=0
a
0
Les oscillations dun systme vibratoire seectuent autour dune position dquilibre stable.
Pour des oscillations de faible amplitude autour de la position dquilibre, tous les mouvements
vibratoires peuvent tre assimils des vibrations linaires et lnergie potentielle peut alors
tre approxime par une forme quadratique de la coordonne q, tandis que lnergie cintique
peut tre approxime par une forme quadratique en q.
2.1.5 Rsolution de lquation direntielle de loscillateur harmonique simple
Lquation direntielle de loscillateur harmonique simple scrit :
q +
2
0
q = 0
La solution dune telle quation est une fonction sinusodale du temps
q(t) = A cos (
0
t +)
H. Djelouah
2.2 Oscillations libres des systmes amortis un degr de libert 9
o A reprsente lamplitude des oscillations, est la phase initiale.
Il est important de remarquer que la pulsation propre
0
ne dpend que des lments qui
constituent le systme physique tudi (masse, ressort, etc...) tandis que lamplitude A et la
phase initiale sont calcules partir des conditions initiales :
_
_
q(t = 0) = q
0
q(t = 0) = q
0
Enn lamplitude des oscillations dun oscillateur harmonique libre ne dpend pas du temps.
De telles oscillations sont dites non amorties.
Il faut nanmoins remarquer quau del dune certaine amplitude la vibration devient non
linaire. Il sensuit dabord une modication de la priode des oscillations et ensuite un change-
ment de la nature du mouvement.
2.2 Oscillations libres des systmes amortis un degr de libert
Dans le paragraphe prcdent, nous navons pas tenu compte de certaines ralits physiques.
En eet, nous navons pas pris en compte les forces de frottement qui sont lorigine de la perte
dnergie mcanique du systme sous forme de chaleur. Dans ce paragraphe, nous allons tenir
compte de ces ralits en nous limitant toutefois au cas simple o les pertes sont dues des
frottements visqueux pour lesquels les forces de frottement, qui sopposent au mouvement, sont
proportionnelles la vitesse.
2.2.1 Equation de Lagrange pour les systmes dissipatifs
Rappelons lquation de Lagrange associe un systme un degr de libert dont lvolution
au cours du temps se ramne ltude de la coordonne gnralise q
d
dt
_
L
q
_
L
q
= F
q
Fq reprsente la composante suivant q de la rsultante des forces gnralises qui ne drivent
pas dun potentiel.
Nous nous intressons au cas particulier des forces de frottement dnies par la force gn-
ralise
F
q
= f
q
= q
o est une constante relle positive.
Lquation de Lagrange scrit alors dans ce cas :
d
dt
_
L
q
_
L
q
= q
2.2.2 Cas particulier des oscillations de faible amplitude
Nous avons montr dans le chapitre prcdent que dans le cas des oscillations de faible
amplitude, la fonction de Lagrange scrivait sous la forme :
L =
1
2
a q
2
1
2
b q
2
Lquation direntielle du mouvement scrit alors :
a q +bq = q
H. Djelouah
Cest une quation direntielle du second ordre coecients constants qui peut se mettre
sous la forme :
q + 2 q +
2
0
q = 0
o est un coecient positif, appel facteur (ou coecient) damortissement et dni par :
=

2 a
0
0
est la pulsation propre dnie par
0
=
b
0
a
0
2.2.3 Rsolution de lquation direntielle
La solution de lquation direntielle dpend de la valeur de par rapport
0
:
Si >
0
, on dit que le systme est suramorti ou apriodique.
Si =
0
, on dit que lon a un amortissement critique.
Si <
0
, on dit que le systme est sous-amorti ou pseudopriodique.
Cas o le systme est suramorti ( >
0
)
La solution de lquation direntielle scrit dans ce cas :
q(t) = A
1
e
_
2
0
t
+A
2
e
_
+
2
0
t
A
1
et A
2
sont des constantes dintgration dnies par les conditions initiales. La gure ci-
dessous reprsente q en fonction du temps dans le cas particulier o q(0) = q
0
et q(0) = 0.
q(t) est une fonction qui tend exponentiellement (sans oscillation) vers zro.
O
Rgime fortement amorti : variation de q en fonction du temps
Cas de lamortissement critique ( =
0
)
La solution gnrale de lquation direntielle est de la forme :
q(t) = (A
1
+A
2
t) e
t
Dans le cas particulier o q(0) = q
0
et q(0) = 0,
q(t) = q
0
(1 + t) e
t
q(t) est encore une fonction qui tend vers zro sans oscillation lorsque le temps augmente.
H. Djelouah
O
Amortissement critique : variation de q en fonction du temps
Cas o le systme est sous-amorti ( <
0
)
q(t) = A e
t
cos (
A
t +)
avec
A
=
_
2
0

2
; A et sont deux constantes dintgration dtermines partir des
conditions initiales. Dans le cas particulier o q(0) = q
0
et q(0) = 0, on obtient :
A =

0
A
q
0
= arctan
_

A
_
O
Systme faiblement amorti : variation de q en fonction du temps
Exercices
Exercice 1 : Calculer la frquence des oscillations pour chacun des systmes suivants dans
lesquels la masse m est astreinte un mouvement vertical uniquement :

m
m
m
k
1
k
2
k
1
k
1
k
2
k
2
H. Djelouah
Exercice 2 : Une masse ponctuelle m glisse sans frottement sur une table horizontale. Elle
est xe deux btis xes par deux cordes de masse ngligeable tendues horizontalement. En
supposant que la tension T des cordes reste constante lors du mouvement, calculer la priode
des oscillations pour de faibles amplitudes du mouvement dans la direction x.

L/2 L/2
m
x
Exercice 3 : Un iceberg de masse volumique
G
, assimilable un paralllpipde rgulier et
homogne de masse M otte sur de leau de masse volumique constante
E
. Sa surface de base
est S et sa hauteur est L.

On rappelle que la pousse dArchimde qui sexerce sur un objet immerg est :

P
A
=
E
V g
o V est le volume immerg et g lacclration de la pesanteur.
1. Calculer, lquilibre, le volume immerg de liceberg en fonction de son volume total. La
masse volumique de la glace est
G
= 900 kg/m
3
; celle de leau est
E
= 1000 kg/m
3
.
2. Liceberg est cart dune distance verticale h par rapport sa position dquilibre. Calculer
la priode de ses oscillations quand les frottements sont considrs comme ngligeables.
Faire lapplication numrique pour L = 150 m, h = 2 m, g = 9.8 m/s
2
.
Exercice 4 : Une tige dacier de constante de torsion ( est soude par son extrmit au centre
dun disque homogne de masse M et de rayon R. Lautre extrmit est encastre dans un bti
xe. Une masse m est soude au point le plus bas du disque.

C
m
M,R
On tourne le disque dun angle
0
et on le lche sans vitesse initiale. Dterminer lexpression en
fonction du temps de langle (t) dcart du systme par rapport sa position dquilibre. On
nglige la exion de la tige dacier.
Exercice 5 : Un mtronome est schmatis sur la gure ci-dessous. La masse M est soude
lextrmit de la tige. La position de la masse m sur la tige peut tre rgle. La tige est suppose
de masse ngligeable ; elle est mobile sans frottements autour de O. La masse M tant en bas,
on lcarte dun angle
0
petit et on labandonne sans vitesse initiale.

M
m
L
l
O
x
y
H. Djelouah
1. Quelle(s) condition(s) doit satisfaire le systme pour quil puisse osciller ?
2. Dterminer lexpression de la priode pour des oscillations de faibles amplitudes.
3. Sachant que M = 80 g, m = 20 g et L = 4 cm, dterminer la distance pour que la
priode du mtronome soit gale 2 s.
4. On veut augmenter la priode doscillation du mtronome. Faut-il rapprocher ou loigner
la masse m du point O?
Exercice 6 : Dans les gures ci-dessous, une tige homogne de masse M et de longueur L
oscille sans frottement, dans un plan vertical, autour dun axe xe perpendiculaire au plan du
mouvement en O.
1. Quelle est la dformation du ressort lquilibre, sachant qu cette position = 0 ?
2. Etablir lquation direntielle du mouvement dans le cas des mouvements de faible am-
plitude.
3. A quelle condition le systme de la gure (b) peut-il osciller ? Quelle est la nature du
mouvement lorsque cette condition nest pas satisfaite ?

M
a
a
a
k
k k
O
O
O
L
L
L
A
A A
(a) (b) (c)
M
M
Exercice 7 : Quand llectron dun atome dhydrogne, se dplace dune petite distance x
partir de la position dquilibre, il subit une force de rappel donne par :
F = kx, avec k =
e
2
4
0
r
2
,
o r = 0.05 nm correspond au rayon de latome. Calculer la pulsation propre
0
des os-
cillations de llectron. On donne e = 1.6 10
19
C, m
e
= 9.1 10
31
kg,
0
= 8.85
10
12
N
1
m
2
C
2
.
Exercice 8 : Calculer la priode des oscillations dune particule de charge q et de masse
m astreinte se dplacer selon une trajectoire rectiligne entre deux charges gales q xes en
x = a.
Exercice 9 : Une particule de masse m se dplace dans un champ de force conservatif avec
une nergie potentielle donne par :
V (x) =
_
1
2
k
_
a
2
x
2
_
pour [x[ < a
0 pour [x[ a
o a et k sont des constantes. Sachant que a > 0, tudier les types de mouvement possibles selon
le signe de k.
Exercice 10 : Lnergie potentielle dune particule de masse m est
V (x) =
c x
x
2
+a
2
o c et a sont des constantes positives. Reprsenter graphiquement V en fonction de x. Etudier
le mouvement des oscillations de faible amplitude au voisinage de la position dquilibre stable.
Sachant que cette particule dmarre de sa position dquilibre stable avec une vitesse v, trouver
les valeurs de v pour lesquelles :
H. Djelouah
1. elle oscille au voisinage de la position dquilibre ;
2. elle schappe vers +;
3. elle schappe vers .
Exercice 11 : Une particule de masse m se dplace dans la rgion x > 0 sous laction dune
force F(x) :
F (x) = m
2
_
x
a
4
x
3
_
o et a sont des constantes. Reprsenter graphiquement lnergie potentielle en fonction de
x. Calculer la priode des oscillations de faible amplitude au voisinage de la position dquilibre
stable. La particule dmarre de cette position avec une vitesse v. Trouver les valeurs de x limitant
la rgion des oscillations. Montrer que la priode des oscillations est indpendante de v. (Astuce
pour le calcul de lintgrale : faire le changement de variable y = x
2
)
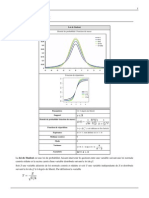
Exercice 12 : Un bloc de masse 25 kg est mont sur un support en caoutchouc, de masse ngli-
geable, qui se comprime de 6.1 cm sous ce poids. Quand le bloc vibre librement, on enregistre les
positions de la masse aprs lavoir dplac de 5 cm partir de sa position dquilibre (voir gure
ci-dessous). Sachant que le tapis de caoutchouc peut tre symbolis par un ressort de raideur K
associ un amortisseur de coecient de frottement visqueux , calculer ces coecients K et
.

x
(
c
m
)
0,0 0,5 1,0 1,5 2,0
-6
-4
-2
0
2
4
6
t(s)
Exercice 13 : Le systme de la gure ci-dessous est constitu dun cylindre homogne de masse
M et de rayon R en rotation autour de son axe de rvolution xe (). Un l inextensible, de
masse ngligeable, entrane le cylindre sans glissement sur sa priphrie ; ses deux extrmits
sont relies un bti xe (B) par un ressort de raideur K et un amortisseur de coecient de
frottement visqueux . Quelle la valeur critique du coecient
C
?

K
R
(B)
(D)
a
Exercice 14 : Le systme mcanique de la gure ci-dessous est constitu dune tige rectiligne
AD, homogne, de masse M = 3 kg et de longueur L = 2 m. Cette tige peut tourner, dans le plan
vertical, sans frottement, autour dun axe horizontal () xe. Les extrmits A et D de la tige
sont relies au bti xe B
2
par deux amortisseurs identiques de coecient de frottement visqueux
. Le point C, milieu de la tige, est reli au bti B
1
par un ressort de raideur k. A lquilibre,
H. Djelouah
la tige est horizontale. Lorsque la tige est carte de sa position dquilibre dun angle
0
puis
lche sans vitesse initiale, elle prend un mouvement oscillatoire amorti de pseudo-priode 1
s. On constate quau bout de 5 pseudo-priodes, lamplitude est gale 20 % de lamplitude
initiale. En dduire la valeur numrique de puis celle de k.

k
A
D
a
a
2a
(B )
1
(B )
2
C
( ) D
a
a
j
H. Djelouah
H. Djelouah
Chapitre 3
Oscillations forces des systmes
un degr de libert
3.1 Equation direntielle
Rappelons la forme gnrale de lquation de Lagrange pour les systmes un degr de
libert :
d
dt
_
L
q
_
L
q
+
T
q
= F
qext
o F
qext
est la force gnralise associe

F
ext
et o la fonction dissipation est T =
1
2
q
2
.
Pour les oscillations de faible amplitude, la fonction de Lagrange pouvait se mettre sous une
forme quadratique de q et q
L =
1
2
a
0
q
2
1
2
b
0
q
2
Do lquation direntielle du mouvement
a
0
q + q +b
0
q = F
qext
Cette quation peut se mettre sous la forme dune quation direntielle du second ordre
coecients constants, avec second membre
q + 2 q +
2
0
q = A(t)
avec
=

2a
0
0
=
b
0
a
0
A(t) =
Fqext
a
0
3.2 Systme masse-ressort-amortisseur
Considrons lexemple mcanique de la gure ci-dessous soumis une force extrieure

F(t)
applique la masse m.
H. Djelouah
18 Oscillations forces des systmes un degr de libert
m
F(t)
k
x
Systme masse-ressort-amortisseur
Calculons la force gnralise F
x
conjugue de la coordonne x. Pour cela nous pouvons
utiliser lune des deux mthodes suivantes :
Soit calculer le travail W de la force

F(t) pour une variation r de son point dapplication
W =

F r = F dx
On en dduit la x-composante de la force extrieure
F
x
=
W
x
= F(t)
Soit utiliser la dnition de la force gnralise
F
x
=

F
r
x
= F(t)
Lquation direntielle du mouvement scrit alors
x + 2 x +
2
0
x = A(t)
avec :
=

2m
,
0
=
k
m
et A(t) =
F(t)
m
3.3 Solution de lquation direntielle
La solution de cette quation direntielle du second ordre est gale la somme de la solution
de lquation sans second membre (ou solution homogne) x
H
(t) et dune solution particulire
de lquation avec second membre x
P
(t) :
x(t) = x
H
(t) +x
P
(t)
Nous avons dj tudi lquation sans second membre x
H
(t) et nous savons que cette solution
contient dans tous les cas le terme exponentiel e
t
. Aprs un intervalle de temps t suprieur
3/ ou 4/, le terme e
t
devient trs petit et la solution homogne est alors pratiquement nulle.
Il ne subsistera que la solution particulire de lquation avec second membre. Lintervalle de
temps pendant lequel la solution homogne est non ngligeable est appel le rgime transitoire.
A la n de ce rgime transitoire commence lintervalle de temps pour lequel la solution homogne
est quasi-nulle et pour lequel la solution x(t) x
p
(t) ; ce rgime est appel rgime permanent
ou stationnaire.
H. Djelouah
3.3 Solution de lquation direntielle 19
3.3.1 Cas particulier o A(t) = A
0
cos(t)
Calcul de la solution permanente laide de la mthode des nombres complexes
Pour t susamment grand, nous pouvons considrer que la solution transitoire sest annule
et que la solution x(t) sidentie alors avec la solution particulire : x(t) x
P
(t). Par commodit
de notation lindice p est sous-entendu dans ce qui suit. La mthode des nombres complexes
permet de calculer aisment la solution stationnaire.
Soit le dplacement complexe reprsent par le nombre complexe A = X e
it
, avec X =
X
0
e
i
. Nous pouvons considrer, en outre, que A(t) = A
0
cos(t) constitue la partie relle du
nombre complexe / = A
0
e
it
. Lquation direntielle se transforme en une simple quation
algbrique en fonction de lamplitude complexe X :
__
2
0

2
_
+i 2
_
X = A
0
dont la solution est :
X =
A
0
_
2
0

2
_
+i 2
Do lon tire lamplitude X
0
et la phase :
X
0
=
A
0
_
_
2
0

2
_
2
+ 4
2
2
= arctan
2
2
0

2
Etude des variations de lamplitude et de la phase en fonction de la pulsation de
lexcitation
Le maximum de lamplitude est obtenu pour la valeur de qui annule
dX
0
d
.
Il existe un maximum la pulsation
R
=
_
2
0
2
2
seulement si lamortissement est
susamment faible pour que <
0
/
2. A cette pulsation, appele pulsation de rsonance, on

dit que le systme entre en rsonance et lamplitude X
0
est maximale ; elle vaut :
X
0 max
=
A
0
2
_
2
0

2
La gure reprsentant les variations de X
0
en fonction de la pulsation dexcitation est
appele courbe de rsonance en amplitude. On remarque qu la pulsation
0
, le dphasage
est gal
2
, et qu la rsonance = arctan
_
_
_
2
0
2
2
_
_
.
H. Djelouah
Amplitude X
0
en fonction de .
Dphasage en fonction de .
Etude de la rsonance pour les faibles amortissements
Dans le cas des faibles amortissements ( <<
0
), la frquence de rsonance est trs peu
dirente de la pulsation propre,
R

0
. Dans ce cas, lamplitude de vibration la rsonance
X
0 max
est gale :
X
0 max
=
A
0
2
0
Pour les faibles amortissements, X
0 max
est donc inversement proportionnel .
Etude de la vitesse
En notation complexe, la vitesse scrit :
1(t) =
dA
dt
= iA =

X e
it
o lamplitude complexe de la vitesse est dnie par
X = iX =
i A
0
_
2
0

2
_
+i 2
Ltude des variations de lamplitude de la vitesse en fonction de la pulsation dexcitation
montre que, quelle que soit la valeur de , la rsonance en vitesse est obtenue pour =
0
(voir
gure ci-dessous). La valeur maximale de lamplitude de la vitesse vaut dans ce cas :
X
max
=

X(
0
) =
A
0
2
Courbe de rsonance de la vitesse
???
Dphasage de la vitesse en fonction de
.
H. Djelouah
3.3 Solution de lquation direntielle 21
Bilan nergtique
Soit P
F
(t) la puissance instantane fournie par la force extrieure F(t) au systme. En rgime
permanent, on obtient :
P
F
(t) = F(t) x(t) = F
0

X
0
cos(t) cos(t +)
Soit la valeur moyenne sur une priode de P
F
(t) :
=
1
2
F
0

X
0
cos()
En tenant compte de lexpression de

X
0
en fonction de F
0
, on obtient :
=
1
2

X
2
0
Comparons cette valeur la valeur moyenne de la puissance dissipe par les forces
de frottement de viscosit. La valeur instantane de cette puissance dissipe scrit :
P
D
(t) = x
2
=

X
2
0
cos
2
(t +)
Do lon tire la valeur moyenne sur une priode :
=
1
2

X
2
0
Ltude des variations de la valeur moyenne de la puissance == en
fonction de la pulsation dexcitation montre que la valeur maximale de la puissance moyenne est
obtenue pour =
0
quelle que soit la valeur de . La valeur maximale de la puissance moyenne
dissipe ou fournie vaut dans ce cas

max
=
F
2
0
2
La gure ci-dessous reprsente les variations, en fonction de , de la puissance moyenne
dissipe par les forces de frottements (ou de manire quivalent la puissance moyenne fournie
par la force extrieure ).
Courbe de rsonance pour la puissance
H. Djelouah
Bande passante
On dnit par bande passante, la bande des pulsations autour de =
0
pour lesquelles

max
/2. Les deux pulsations
1
et
2
, situes de part et dautre de la pulsation
0
et pour lesquelles =
max
/2, sont appeles pulsations de coupure. La bande
passante B scrit :
B =
2
1
Le calcul de B consiste rechercher les deux pulsations pour lesquelles =
max
/2.
On obtient lexpression de la bande passante B :
B =
2
1
= 2
Coecient de qualit dun oscillateur
Le coecient de qualit dun oscillateur est dni par le rapport de la pulsation propre
0

la largeur de bande B :
Q =

0
B
3.3.2 Cas dune excitation priodique
Nous avons tudi dans le paragraphe prcdent la rponse dun systme vibratoire une
excitation sinusodale dite excitation harmonique. En pratique, les excitations mcaniques ne
sont pas toujours parfaitement sinusodales ; elles sont souvent priodiques. En considrant le
cas dexcitations priodiques, nous procderons une gnralisation du cas harmonique.
Soit une excitation priodique applique un systme amorti un degr de libert. Lqua-
tion direntielle qui rgit ce systme scrit :
q + 2 q +
2
0
q = A(t)
La fonction A(t) tant priodique, de priode T, son dveloppement de Fourier scrit :
A(t) =
a
0
2
+
n=1
a
n
cos(nt) +b
n
sin(nt)
Lquation direntielle scrit alors :
q + 2 q +
2
0
q =
a
0
2
+
n=1
a
n
cos(nt) +b
n
sin(nt)
La rponse permanente (ou stationnaire ) qui sidentie avec la solution particulire, pour t
susamment lev, peut alors tre calcule pour chacune des composantes de lexcitation : a
0
/2,
a
n
cos(nt) et b
n
sin(nt). On obtient alors par superposition :
q(t) =
a
0
2
2
0
+
n=1
a
n
cos(
n
t +
n
) +b
n
sin(
n
t +
n
)
_
(
2
n
2
0
)
2
+ 4
2
2
n
H. Djelouah
3.4 Impdance mcanique 23
3.4 Impdance mcanique
3.4.1 Dnition
Considrons un systme mcanique soumis une force sinusodale F (t) = F
0
cos (t). En
rgime permanent, le point dapplication de cette force se dplace avec une vitesse v (t) =
V
0
cos (t +) . On appelle impdance mcanique dentre du systme mcanique, le rapport
des amplitudes complexes de la force F et de la vitesse v
Z
E
=
F
V
3.4.2 Impdances mcaniques
Amortisseur
Dans le cas dun amortisseur, la force applique est relie la vitesse par
F = v
On en dduit limpdance complexe dun amortisseur
Z
=
Masse
Dans le cas dune masse, la relation fondamentale de la dynamique scrit
F = m
dv
dt
On en dduit limpdance complexe dune masse
Z
m
= im = me
i
2
Ressort
Dans le cas dun ressort de raideur k, la force applique f applique au ressort sexprime en
fonction de lallongement par
f = k x
On en dduit limpdance complexe dun ressort
Z
k
=
k
i
= i
k
=
k
e
i
2
3.4.3 Puissance
La valeur moyenne, sur une priode, de la puissance fournie est
=
1
2
F
0

X
0
cos () =
1
2
Re
_
Z
E
_

X
2
0
H. Djelouah
3.4.4 Applications
Systme mcanique rsonant
Soit un systme mcanique constitu dun ressort de raideur k, dun amortisseur de coecient
de frottement visqueux et dune masse m soumise une force sinusodale F (t) = F
0
cos (t).
Limpdance dentre de ce systme est
Z
E
= +i
_
m
k
_
A la rsonance
_
=
0
=
_
k
m
_
, le module de limpdance est Z
E
= . Lorsque la pulsation
, limpdance Z
E
im.
Module de limpdance dentre. Amplitude de la vitesse
Systme antirsonant
Considrons un systme mcanique constitu dun ressort de raideur k dont une extrmit
est relie une masse m et dont lautre est soumise une force sinusodale F (t). Soit x le
dplacement de la masse m et soit y le dplacement du point dapplication de la force F (t).
Pour calculer limpdance dentre de ce systme, nous devons dabord crire les quations
direntielles du mouvement :
m x = k (x y)
F = k (x y)
En utilisant la notation complexe, on obtient limpdance dentre :
Z
E
=
F
Y
= i
km
_
m
k
_
La pulsation dantirsonance est
0
=
_
k
m
. Lorsque =
0
, la vitesse

Y est nulle tandis
que le module de limpdance est . Lorsque la pulsation , limpdance Z
E
0.
H. Djelouah
Module de limpdance dentre. Amplitude de la vitesse.
Exercices
Exercice 1 : Un disque circulaire homogne, de masse M, de rayon R, peut osciller sans
frottements autour de son axe horizontal O. Deux masses m
1
et m
2
sont soudes aux extrmits
dune tige de masse ngligeable lie rigidement au disque et passant par O. Les distances de m
1
et m
2
au centre sont notes respectivement
1
et
2
. Un ressort vertical, de constante de raideur
K a une extrmit xe et lautre est relie au disque en un point A situ une distance a de
O. En position dquilibre la tige est verticale avec m
1
en bas et le point A est au mme niveau
que le centre O. Le disque subit un frottement visqueux de coecient au point B. La masse
m
1
est soumise une force F(t) = F
0
cos(t) perpendiculaire la tige. Valeurs numriques :
M = 1 kg, m
1
= m
2
= 0.1 kg, K = 16 N/m, R = 20 cm,
1
= 50cm,
2
= 25cm, a = 10 cm,
g = 10 m/s
2
, = 7.25 10
2
kg/s.

R
K
a
F(t)
m
1
m
2
l
1
l
2
B
A
O
a
1. Etablir lquation direntielle du mouvement.
2. Trouver sa solution en rgime permanent.
3. Calculer le facteur de qualit Q du systme.
4. Dterminer la valeur de F
0
pour qu la rsonance lamplitude maximale soit gale /30
rad.
Exercice 2 : (suite de lexercice n14 du chapitre prcdent) Le bti B
1
est maintenant anim
dun mouvement vertical sinusodal donn par : s(t) = S
0
cos(t) o S
0
= 1 cm.
H. Djelouah
1. Montrer que lquation direntielle qui rgit le mouvement du systme peut scrire :
+ 2

+
2
0
= A
0
cos(t)
On prcisera de manire explicite le terme A
0
. Calculer sa valeur numrique.
2. Quelle est lexpression de la solution (t) lorsque le rgime permanent est tabli ? Vri-
er que le systme est trs faiblement amorti ; en dduire la frquence de rsonance et
lamplitude de (t) la rsonance.
3. Quelle est, la rsonance, lamplitude de la force F
T
transmise au sol par chaque amor-
tisseur ?
Exercice 3 : Le dispositif mcanique ci-dessous reprsente le schma de principe dun appareil
de mesure de vibrations. La masse m est lie par deux ressorts et un amortisseur de coecient de
frottement visqueux un support rigidement li au systme mcanique dont on veut tudier
les vibrations. Le mouvement du support est repr par s(t) tandis que le mouvement de la
masse est repr par x(t). On tudie des vibrations sinusodales de la forme s(t) = S
0
cos(t).
Lorigine est prise la position dquilibre.

x(t)
m
k/2 k/2
s(t)
a
1. Etablir lquation du mouvement de la masse m en fonction de la coordonne relative
y(t) = x(t) s(t).
2. Dterminer la solution stationnaire y(t).
3. Dans le cas de ressorts de faible raideur, la pulsation propre
0
est petite devant la pul-
sation . Donner dans ce cas lexpression de y(t). Montrer que lon peut ainsi dterminer
facilement lamplitude S
0
de la vibration (on a ralis ainsi un vibromtre).
4. Lorsque la raideur des ressorts est leve, la pulsation propre
0
est grande devant la
pulsation des vibrations. Montrer , que dans ce cas on peut dterminer facilement
lacclration du support (on a ainsi ralis un acclromtre).
Exercice 4 : Un vhicule roulant est un systme complexe plusieurs degrs de libert. La
gure ci-dessous peut tre considre comme une premire approximation dun vhicule qui se
dplace sur une route ondule dcrite par le prol y
1
(t).

m
y(t)
y (t)
1
x
x=vt
k
L
Dans ce modle simpli, on suppose que :
La raideur lastique des pneus est innie, cest--dire que les ondulations de la route sont
intgralement transmises la suspension du vhicule.
H. Djelouah
Les roues ne dcollent pas de la chausse.
On sintresse uniquement au dplacement vertical y(t) du vhicule dans le plan de la
gure.
On se place dans le cas simple o le vhicule se dplace horizontalement une vitesse
constante v sur une route prol sinusodal y
1
(x) = Y
1
sin(2x/).
1. Etablir lquation direntielle qui rgit les variations au cours du temps de la coordonne
y du vhicule.
2. En dduire lamplitude Y du mouvement du vhicule dans le sens vertical .
3. Application numrique m = 350 kg, k = 350 kN/m, v = 100 km/h, = 5m, Y
1
= 20 cm;
(a) pour = 2000 N s/m,
(b) pour = 200 N s/m.
Exercice 5 : Les machines tournantes (moteurs lectriques, turbines, machines laver, etc...)
peuvent tre le sige de vibrations importantes car trs souvent le centre de masse ne concide
pas avec laxe de rotation. Pour limiter ces vibrations on utilise des supports antivibratoires
constitus gnralement de caoutchouc renforc. En raison de leurs proprits mcaniques ces
supports peuvent tre modliss par un amortisseur en parallle avec un ressort.
On se propose dtudier titre dexemple le cas dune machine laver le linge (gure 1 ci-
dessous). Soit M la masse de cette machine. La partie tournante est constitue dun tambour de
rayon e tournant une vitesse angulaire constante . On considre que la masse tournante est
constitue par le linge de masse m. Pour des raisons de simplicit, on suppose que le lave-linge
ne peut eectuer que des mouvement verticaux reprs par la coordonne y.

y(t)
k
y(t)
k
M M+m
e
m
F
eq
Figure 2 Figure 1
a a
1. Etablir lquation direntielle du mouvement pour la coordonne y.
2. Montrer quun tel dispositif est quivalent au schma simpli de la gure 2 ci-dessus ;
donner lexpression de F
eq
.
3. Dans lhypothse des faibles amortissements ( <<
0
), tracer et commenter le graphe de
lamplitude Y du dplacement vertical du lave-linge en fonction de la vitesse de rotation.
4. Calculer lamplitude de la force transmise au sol la rsonance.
H. Djelouah
H. Djelouah
Chapitre 4
Oscillations libres des systmes
deux degrs de libert
4.1 Introduction
Les systmes qui ncessitent deux coordonnes indpendantes pour spcier leurs positions
sont appels systmes deux degrs de libert.
Exemples
Figure 1 Si les masses m
1
et m
2
sont astreintes se dplacer verticalement, 2 coordonnes
x
1
et x
2
sont ncessaires pour spcier la position de chaque masse chaque instant.
Figure 2 Si la masse M est astreinte se dplacer dans un plan vertical, deux coordon-
nes sont ncessaires pour spcier la conguration du systme. Lune de ces coordonnes
peut tre le dplacement x qui correspond la translation verticale de la masse. Lautre
coordonne peut tre le dplacement angulaire pour tenir compte de la rotation de la
masse. Ces deux coordonnes sont indpendantes lune de lautre.
Figure 3 Dans le cas du double pendule, deux coordonnes sont ncessaires pour spcier
la position des masses m
1
et m
2
. Plusieurs choix sont pourtant possibles, en eet on peut
choisir (x
1
, x
2
) ou (y
1
, y
2
) ou (
1
,
2
).
Il est possible de spcier la conguration dun systme laide de plusieurs ensembles de
coordonnes indpendantes ; un ensemble quelconque de ces coordonnes est appel coordonnes
gnralises. Il y a autant dquations de Lagrange que de degrs de libert ou de coordonnes
gnralises. Pour ltude des systmes deux degrs de libert, il est ncessaire dcrire deux
H. Djelouah
30 Oscillations libres des systmes deux degrs de libert
quations direntielles du mouvement que lon peut obtenir partir des quations de Lagrange
_
_
d
dt
_
L
q
1
_
L
q
1
= 0
d
dt
_
L
q
2
_
L
q
2
= 0
4.2 Systmes deux degrs de libert
4.2.1 Systme masses-ressorts en translation
Systme masses-ressorts en translation
Considrons le systme ci-dessus, constitu de deux masses m
1
et m
2
relies respectivement
par deux ressorts de raideur k
1
et k
2
deux btis xes. Les deux masses sont relies par un
ressort de raideur K. Ce ressort est appel ressort de couplage.
Equations direntielles du mouvement
Les quations du mouvement pour ce systme deux degrs de libert peuvent tre obte-
nues partir des quations de Lagrange pour chaque coordonne x
1
(t) et x
2
(t). Soit T et U
respectivement lnergie cintique et lnergie potentielle :
T =
1
2
m
1
x
2
1
+
1
2
m
2
x
2
2
U =
1
2
k
1
x
2
1
+
1
2
K (x
1
x
2
)
2
+
1
2
k
2
x
2
2
U =
1
2
(k
1
+K) x
2
1
+
1
2
(k
2
+K) x
2
2
Kx
1
x
2
Le lagrangien L = T U scrit alors
L =
1
2
m
1
x
2
1
+
1
2
m
2
x
2
2
1
2
(k
1
+K) x
2
1
1
2
(k
2
+K) x
2
2
+Kx
1
x
2
Les quations de Lagrange scrivent
_
_
d
dt
_
L
x
1
_

L
x
1
= 0
d
dt
_
L
x
2
_

L
x
2
= 0
Do le systme dquations direntielles du mouvement
_
_
m
1
x
1
+ (k
1
+K) x
1
Kx
2
= 0
m
2
x
2
+ (k
2
+K) x
2
Kx
1
= 0
Les termes Kx
2
et Kx
1
qui apparaissent respectivement dans la premire et la seconde
quation sont appels termes de couplage, et les deux quations direntielles sont dites couples.
H. Djelouah
4.2 Systmes deux degrs de libert 31
Rsolution des quations direntielles
Recherchons une solution particulire de la forme :
x
1
(t) = A
1
cos(t +)
x
2
(t) = A
2
cos(t +)
o A
1
, A
2
et sont des constantes et lune des pulsations propres du systme. La substi-
tution de x
1
et x
2
dans le systme dquations direntielles donne
_
_
_
k
1
+ K m
1
A
1
K A
2
= 0
K A
1
+
_
k
2
+ K m
2
A
2
= 0
Ce qui constitue un systme dquations linaires homognes dont les inconnues sont A
1
et
A
2
. Ce systme admet une solution non identiquement nulle seulement si le dterminant ()
des coecients de A
1
et A
2
est gal zro.
() =
_
k
1
+ K m
1
K
K
_
k
2
+ K m
2
Le dterminant () est appel dterminant caractristique. Lquation () = 0 est appe-

le lquation caractristique ou quation aux pulsations propres. Elle scrit
_
k
1
+ K m
1
2
_ _
k
2
+ K m
2
2
_
K
2
= 0
ou encore
4

2
_
k
1
+ K
m
1
+
k
2
+ K
m
2
_
+
k
1
k
2
+ k
1
K + k
2
K
m
1
m
2
= 0
Cette quation est une quation quadratique en qui admet deux solutions relles positives
1
et
2
appeles les pulsations propres du systme.
Cet exemple montre quil y a en gnral deux pulsations propres dans un systme deux
degrs de libert. Chacune des coordonnes, x
1
et x
2
, possde deux composantes harmoniques
de pulsations
1
et
2
x
1
= A
11
cos(
1
t +
1
) +A
12
cos(
2
t +
2
)
x
2
= A
21
cos(
1
t +
1
) +A
22
cos(
2
t +
2
)
o A
11
, A
12
, A
21
, A
22
,
1
et
2
sont des constantes. Le terme de plus basse frquence
correspondant la pulsation
1
est appel le fondamental. Lautre terme, de pulsation
2
, est
appel harmonique.
Les doubles indices sont utiliss pour les amplitudes des direntes composantes harmo-
niques ; le premier indice se rfre la coordonne et le second la pulsation. Par exemple A
12
est lamplitude de x
1
(t) la pulsation
2
.
Lorsque A
12
= A
22
= 0, x
1
et x
2
correspondant la premire solution particulire sont des
fonctions sinusodales, en phase, de pulsation
1
; on dit que le systme oscille dans le premier
mode. Dans ce cas
x
1
= A
11
cos(
1
t +
1
)
x
2
= A
21
cos(
1
t +
1
)
H. Djelouah
Lorsque A
11
= A
21
= 0, x
1
et x
2
correspondant la seconde solution particulire et sont des
fonctions sinusodales, en opposition de phase, de pulsation
2
; on dit que le systme oscille
dans le second mode. Dans ce cas
x
1
= A
12
cos(
2
t +
2
)
x
2
= A
22
cos(
2
t +
2
)
Etudions les particularits de ces deux solutions particulires :
La premire solution particulire scrit :
x
1
= A
11
cos(
1
t +
1
)
x
2
= A
21
cos(
1
t +
1
)
x
1
et x
2
doivent vrier le systme dquations direntielles, ce qui donne
_
_
_
k
1
+ K m
1
2
1
A
11
K A
21
= 0
K A
11
+
_
k
2
+ K m
2
2
1
A
21
= 0
Ces deux quations permettent dobtenir le rapport des amplitudes dans le premier mode
ou fondamental
1
=
A
21
A
11
=
k
1
+ K m
1
2
1
K
=
K
k
2
+ K m
2
2
1
La seconde solution particulire scrit :
x
1
= A
12
cos(
2
t +
2
)
x
2
= A
22
cos(
2
t +
2
)
x
1
et x
2
doivent vrier le systme dquations direntielles, ce qui donne
_
_
_
k
1
+ K m
1
2
2
A
12
K A
22
= 0
K A
12
+
_
k
2
+ K m
2
2
2
A
22
= 0
Ces deux quations permettent dobtenir le rapport des amplitudes dans le second mode
ou harmonique
2
=
A
22
A
12
=
k
1
+ K m
1
2
2
K
=
K
k
2
+ K m
2
2
2
La solution gnrale (x
1
, x
2
) est une combinaison linaire de ces deux solutions particu-
lires. x
1
et x
2
scrivent alors
x
1
= A
11
cos (
1
t +
1
) +A
12
cos (
2
t +
2
)
x
2
=
1
A
11
cos (
1
t +
1
) +
2
A
12
cos (
2
t +
2
)
o A
11
, A
12
,
1
et
2
sont des constantes dintgration dont les valeurs sont xes par les
conditions initiales.
H. Djelouah
4.2.2 Cas particulier de deux oscillateurs identiques
Calcul des constantes dintgration
Considrons le cas particulier de deux oscillateurs identiques tels que m
1
= m
2
= m et
k
1
= k
2
= k. Dans ce cas les pulsations propres sont respectivement gales
1
=
_
k
m
2
=
_
k + 2 K
m
=
1
_
1 +
2 K
k
Les rapports damplitudes correspondant ces pulsations sont respectivement
1
= +1 et
2
= 1.
Soit x
10
, x
20
, x
10
et x
20
les valeurs initiales respectives de x
1
, x
2
, x
1
et x
2
. Tenant compte de
ces conditions initiales, on obtient le systme dquations suivant qui permet de dterminer les
constantes dintgration A
11
, A
12
,
1
et
2
A
11
cos(
1
) +A
12
cos(
2
) = x
10
A
11
cos(
1
) A
12
cos(
2
) = x
20
1
A
11
sin(
1
)
2
A
12
sin(
2
) = x
10
1
A
11
sin(
1
) +
2
A
12
sin(
2
) = x
20
Les solutions de ce systme dquations sont
A
11
=
x
10
+x
20
2 cos(
1
)
et A
12
=
x
10
x
20
2 cos(
2
)
ou encore
A
11
=
x
10
+ x
20
2
1
sin(
1
)
et A
12
=
x
20
x
10
2
2
sin(
2
)
1. Considrons le cas particulier suivant x
10
= x
20
= x
0
et x
10
= x
20
= 0 ; on obtient dans
ce cas
1
=
2
= 0 , A
12
= 0 et A
11
= x
0
; do
x
1
= x
0
cos(
1
t)
x
2
= x
0
cos(
1
t)
Pour ces conditions initiales particulires, les deux masses oscillent en phase la mme
pulsation
1
. On dit que le systme oscille dans le mode fondamental.
-x
0
x
0
x
1
x
2
temps
temps
-x
0
x
0
Oscillations dans le mode fondamental
H. Djelouah
2. Considrons un autre cas particulier pour lequel x
10
= x
20
= x
0
et x
10
= x
20
= 0 . On
obtient dans ce cas
1
=
2
= 0, A
11
= 0 et A
12
= x
0
; do
x
1
= x
0
cos(
2
t)
x
2
= x
0
cos(
2
t)
On dit que le systme oscille dans le second mode car les deux masses oscillent en opposition
de phase avec la mme pulsation
2
.
x
0
-x
0
x
1
x
2
temps
temps
x
0
-x
0
Oscillations dans le mode harmonique
3. Considrons enn le cas particulier suivant x
10
= x
0
, x
20
= 0 et x
10
= x
20
= 0 ; do
1
=
2
= 0, A
11
= A
12
= x
0
/2. Les solutions scrivent alors sous la forme
x
1
(t) =
x
0
2
cos (
1
t) +
x
0
2
cos (
2
t)
x
2
(t) =
x
0
2
cos (
1
t)
x
0
2
cos (
2
t)
Les solutions ne sont plus des fonctions purement sinusodales du temps mais des combi-
naisons linaires de deux fonctions sinusodales de pulsations respectives
1
et
2
. x
1
et
x
2
peuvent scrire sous la forme
x
1
(t) = x
0
cos
_
1
2
t
_
cos
_
2
+
1
2
t
_
x
2
(t) = x
0
sin
_
1
2
t
_
sin
_
2
+
1
2
t
_
La gure suivante reprsente le rsultat obtenu dans le cas o
1
est trs dirent de
2
(cest- -dire si K >> k).
x
0
0
-x
0
-x
x
0
temps
temps
x
1
x
2
Oscillations dans le cas des conditions initiales : x
10
= x
0
, x
20
= 0 et x
10
= x
20
= 0
H. Djelouah
Si
1
est peu dirent de
2
(cest- -dire si K << k), on observe un phnomne de
battement (voir gure ci-dessous).
temps
temps
-x
0
x
0
x
1
x
2
-x
0
x
0
Phnomne de battements
Coordonnes principales
Considrons les coordonnes p
1
et p
2
obtenues partir des coordonnes x
1
et x
2
par les
relations
p
1
=
x
1
+ x
2
2
p
2
=
x
1
x
2
2
Tenant compte des expressions de x
1
et x
2
et des valeurs particulires de
1
et
2
pour
lexemple tudi, on obtient
p
1
=
x
0
2
cos (
1
t)
p
2
=
x
0
2
cos (
2
t)
On remarque que, quelles que soient les conditions initiales, p
1
et p
2
sont des fonctions
purement sinusodales du temps de pulsations respectives
1
et
2
. Ces coordonnes particulires
sont appeles coordonnes principales. On peut vrier que le systme dquations direntielles
qui rgit le mouvement du systme considr scrit sous la forme de deux quations dcouples
p
1
+
2
1
p
1
= 0
p
2
+
2
2
p
2
= 0
Les relations inverses suivantes
x
1
= p
1
+p
2
x
2
= p
1
p
2
permettent dobtenir les coordonnes x
1
et x
2
partir des coordonnes principales p
1
et p
2
.
H. Djelouah
4.2.3 Pendules coupls
Considrons le cas de deux pendules simples identiques coupls par un ressort de raideur K
et qui eectuent des oscillations de faible amplitude repres par les angles
1
et
2
.
Pendules coupls
Etablissons tout dabord les quations direntielles du mouvement dans le cas des oscilla-
tions de faible amplitude. Il est ais de montrer que lnergie cintique et lnergie potentielle
scrivent sous les formes quadratiques suivantes
T =
1
2
ml
2

2
1
+
1
2
ml
2

2
2
U =
1
2
_
Kl
2
+mgl
2
1
+
1
2
_
Kl
2
+mgl
2
2
Kl
2
2
On remarque la prsence du terme de couplage Kl
2
2
dans lexpression de lnergie
potentielle. Comme dans lexemple prcdent, on dit que le couplage est lastique. Si le terme
de couplage nexiste que dans lexpression de lnergie cintique, on dit que le couplage est de
type inertiel.
Les quations de Lagrange permettent dobtenir les quations direntielles du mouvement
ml
2
1
+
_
Kl
2
+mgl
1
Kl
2
2
= 0
Kl
2
1
+ml
2
2
+
_
Kl
2
+mgl
2
= 0
En labsence damortissement une solution particulire de ce systme dquations diren-
tielles serait
1
(t) = A
1
cos(t +)
2
(t) = A
2
cos(t +)
Ces deux expressions doivent satisfaire le systme dquations direntielles, do
_
Kl
2
+mgl ml
2
A
1
Kl
2
A
2
= 0
Kl
2
A
1
+
_
Kl
2
+mgl ml
2
A
2
= 0
Ce systme dquations admet des solutions non nulles seulement si est solution de lqua-
tion aux frquences
H. Djelouah
_
Kl
2
+mgl ml
2
2
_
2
K
2
l
4
= 0
Do lon tire lexpression des pulsations propres
1
et
2
1
=
_
g
l
et
2
=
g
l
+
2K
m
La solution du systme dquations direntielles est donc
1
= A
11
cos(
1
t +
1
) +A
12
cos(
2
t +
2
)
2
= A
21
cos (
1
t +
1
) +A
22
cos (
2
t +
2
)
Pour calculer les rapports des amplitudes dans les modes, on suppose que le systme oscille
soit dans le premier mode soit dans le second mode. Dans le premier mode, on obtient le systme
_
Kl
2
+mgl ml
2
2
1
Kl
2
1
= 0
Kl
2
+
_
Kl
2
+mgl ml
2
2
1
1
= 0
Dans le second mode, on obtient
_
Kl
2
+mgl ml
2
2
2
Kl
2
2
= 0
Kl
2
+
_
Kl
2
+mgl ml
2
2
2
2
= 0
Tenant compte des expressions de
1
et
2
on obtient les valeurs du rapport des ampli-
tudes dans les modes
1
= +1 et
2
= 1. Les solutions du systme dquations direntielles
scrivent alors
1
= A
11
cos (
1
t +
1
) +A
12
cos (
2
t +
2
)
2
= A
11
cos (
1
t +
1
) A
12
cos (
2
t +
2
)
Exercices
Exercice 1 : Soit le systme mcanique reprsent par la gure ci-contre, compos de deux
oscillateurs linaires (m, k) coupls par un ressort de raideur k
.

m m
k
k
k'
x
1
x
2
1. Ecrire le lagrangien du systme.
2. (a) Mettre ce Lagrangien sous la forme :
L =
1
2
m
__
x
2
1
+ x
2
2
_
2
0
_
x
2
1
+x
2
2
2Cx
1
x
2
__
Donner les expressions de
2
0
et C (coecient de couplage).
(b) En dduire les quations du mouvement.
3. (a) Dterminer les pulsations propres du systme.
H. Djelouah
(b) Sachant que T
0
= 2/
0
= 0, 5 s et C = 0, 3, calculer les valeurs numriques des
priodes propres.
4. (a) Le coecient de couplage C tant faible, donner les solutions x
1
(t) et x
2
(t) avec les
conditions initiales suivantes : t = 0 s, x
1
(0) = X
0
, x
1
(0) = 0 et x
2
(0) = 0, x
2
(0).
Quel phnomne physique observe-t-on?
(b) Tracer lallure des courbes reprsentatives de x
1
(t) et x
2
(t).
Exercice 2 : Soit le systme mcanique reprsent gure ci-dessous. Les variables x
1
(t) et x
2
(t)
reprsentent les dplacements horizontaux ( partir de lquilibre) des masses m
1
et m
2
dans le
cas des petites oscillations. La tige de longueur L est de masse ngligeable.

K
1
K
2
K
3
m
1
m
2
L/2
L/2
x
1
x
2
On se place dans le cas o : K
1
= K
2
= K
3
= k et m
1
= m
2
= m. On posera :
2
0
=
_
5k
4m
+
g
L
_
=
2k
m
1. Calculer les pulsations propres
2. Dterminer les rapports des amplitudes de chacun des modes.
3. En dduire lexpression de x
1
(t) et x
2
(t).
4. Donner les solutions de x
1
(t) et x
2
(t) si x
1
(0) = x
0
, x
1
(0) = 0 et x
2
(0) = 0, x
2
(0) = 0
Exercice 3 : Soit le systme mcanique suivant comprenant entre autres une barre horizontale
de masse ngligeable et qui peut pivoter sans frottement autour dun axe passant par son milieu.

m
M
y
L
k
3
k
2
k
3
m
L
j
On prendra M = 2m et k
1
= k
2
= k
3
= k
1. Etablir les quations rgissant les petites oscillations.
2. Trouver les pulsations propres et les rapports des amplitudes pour les dirents modes.
3. Ecrire les solutions gnrales y(t) et (t).
Exercice 4 : Dans la gure ci-dessous, M et R reprsentent respectivement la masse et le
rayon de la poulie. x
1
et x
2
reprsentent les carts des deux masses par rapport leur position
dquilibre.
H. Djelouah

m
1
m
2
k
1
k
0
k
2
M
x
1
x
2
On prend : M = 2(m
2
m
1
) avec m
2
= m, et k
0
= k
1
= k
2
= k.
1. Ecrire le Lagrangien du systme.
2. Dterminer les pulsations propres et le rapport des amplitudes de chacun des modes en
fonction de m et k.
Exercice 5 : Sur la gure ci-dessous, nous avons schmatis un vhicule avec sa suspension
(sans amortisseurs). Nous supposons que les ressorts restent verticaux. La masse du vhicule est
m et son moment dinertie par rapport un axe horizontal D passant par le centre de gravit G
et perpendiculaire au plan de la gure est J
0
. Le dplacement du centre de gravit par rapport
lquilibre est repr par x (pompage). Langle (tangage) que fait le chassis avec le sol, par
rotation autour de D, sera suppos petit. Linclinaison sur les cts (roulis) est suppose nulle.

x
G
L
1
L
2
k
1
k
2
j
On donne les valeurs suivantes :
masse du vhicule m = 1000 kg,
distance entre laxe avant et G : L
1
= 1 m,
distance entre laxe arrire et G : L
2
= 1.5 m,
constante de raideur du ressort avant : k
1
= 18 kN/m,
constante de raideur du ressort arrire : k
2
= 18 kN/m,
moment dinertie du vhicule : J
0
= mr
2
; r = 0.9 m.
1. Dterminer les pulsations propres du systme ainsi que le rapport des amplitudes dans
chacun des modes.
2. Ecrire les solutions x(t) et (t).
3. (a) Quelle condition doit tre ralise si lon dsire avoir un dcouplage entre x et ?
(b) Quelles sont alors les frquences propres de pompage f
P
et de tangage f
T
?
H. Djelouah
H. Djelouah
Chapitre 5
Oscillations forces des systmes
deux degrs de libert
5.1 Equations de Lagrange
Soit un systme deux degrs de libert, soumis des forces qui drivent dun potentiel,
des forces de frottement de viscosit et des forces extrieures. Si les coordonnes gnralises
sont q
1
et q
2
, les quations de Lagrange scrivent :
d
dt
_
L
q
1
_
L
q
1
+
T
q
1
= F
q
1
d
dt
_
L
q
2
_
L
q
2
+
T
q
2
= F
q
2
Dans cette expression F
q
1
et F
q
2
sont les forces gnralises conjugues des coordonnes
gnralises respectives q
1
et q
2
. Elles sont respectivement dnies par
F
q
1
=
W
1
q
1
q
1
=0
q
2
=0
, dans cette expression W
1
reprsente le travail des forces extrieures
pour une variation q
1
de la coordonne q
1
, lorsque q
2
= 0.
F
q
2
=
W
2
q
2
q
1
=0
q
2
=0
, dans cette expression W
2
reprsente le travail des forces extrieures
pour une variation q
2
de la coordonne q
2
, lorsque q
1
= 0.
5.2 Systme masses-ressorts-amortisseurs
Systme deux degrs de libert en oscillations forces.
Pour tudier les particularits des oscillations forces des systmes deux degrs de libert,
tudions le systme symtrique de la gure ci-dessus, soumis une force horizontale F applique
la premire masse.
H. Djelouah
42 Oscillations forces des systmes deux degrs de libert
5.2.1 Equations direntielles
Les quations direntielles du mouvement scrivent :
m x
1
+ (k +K) x
1
+ x
1
Kx
2
= F
Kx
1
+m x
2
+ (k +K) x
2
+ x
2
= 0
5.2.2 Etude du rgime permanent sinusodal
Solution permanente
La solution gnrale de systme dquations direntielles est gale somme de la solution du
systme homogne et dune solution particulire. La solution de lquation homogne, en raison
de lamortissement, tend vers zro lorsque le temps augmente. Lorsque le rgime permanent
stablit, la solution devient gale la solution permanente et scrit alors :
x
1
= X
1
cos (t +
1
)
x
2
= X
2
cos (t +
2
)
Pour calculer les amplitudes X
1
et X
2
, ainsi que les phases
1
et
2
, utilisons la mthode
des nombres complexes. On peut ainsi crire :
x
1
= Re
_
X
1
e
it
_
x
2
= Re
_
X
2
e
it
_
F = Re
_
F e
it
_
Dans ces expressions les amplitudes complexes sont dnies par
X
1
= X
1
e
i
1
X
2
= X
2
e
i
2
F = F
0
e
i0
Dans ce cas les quations direntielles se transforment en quations algbriques :
_
_
_
k +K m
2
+i
_
X
1
KX
2
= F
KX
1
+
_
k +K m
2
+i
_
X
2
= 0
Amortissement ngligeable
Considrons dabord le cas dun amortissement susamment faible pour que lon puisse
considrer que 0. Le systme dquations direntielles scrit alors
_
_
_
k +K m
2
_
X
1
KX
2
= F
KX
1
+
_
k +K m
2
_
X
2
= 0
Les solutions de ce systme sont :
X
1
=
F
m
_
2
A
2
_
_
2
1

2
_ _
2
2

2
_
X
2
=
KF
m
2
1
_
2
1

2
_ _
2
2

2
_
H. Djelouah
5.3 Impdance 43
Les pulsations
1
=
_
k
m
et
2
=
_
k + 2K
m
sont les pulsations propres calcules au chapitre
prcdent. La valeur de la pulsation
A
est :
A
=
k +K
m
Les amplitudes des dplacements X
1
et X
2
sont alors donnes par
X
1
=
F
0
m
2
A
2
1

2
2
2

2
X
2
=
K F
0
m
2
1
2
1

2
2
2

2
Les variations des amplitudes X

1
et X
2
sont reprsentes sur les gures ci-dessous.
0,0 0,5 1,0 1,5 2,0 2,5 3,0
0
5
10
A

2
1
X
1
Variation de X
1
en fonction de
0,0 0,5 1,0 1,5 2,0 2,5 3,0
0
5
10

A

2
1
X
2
Variation de X
2
en fonction de
On remarque que le phnomne de rsonance se produit pour X
1
comme pour X
2
lorsque la
pulsation dexcitation est gale lune des pulsations propres
1
ou
2
du systme. Lamortis-
sement tant trs faible, les amplitudes la rsonance sont trs importantes. Lorsque la pulsation
devient trs grande, ces amplitudes tendent vers zro. Enn lorsque =
A
, lamplitude X
1
est gale zro ; pour cette raison, la pulsation
A
est appele pulsation dantirsonance.
5.3 Impdance
Considrons le systme deux degrs de libert tudi dans le paragraphe prcdent dans
lequel nous supposons que lamortissement est nul ( 0). En rgime stationnaire, on obtient
pour lamplitude complexe de la vitesse

X
1
:
X
1
= i
2
A
_
2
1
_ _
2
2
_F
On en dduit limpdance dentre :
Z
E
=
F
X
1
= i
m
2
1
_ _
2
2
_
2
A
Les gures ci-dessous donnent les variation de

X et Z
E
en fonction de . On note le ph-
nomne de rsonance lorsque la pulsation dexcitation est gale lune des deux pulsations
propres
1
ou
2
. A ces pulsations, le module de limpdance dentre est nul. Enn, lorsque
est gale la pulsation dantirsonance
A
, la vitesse de la premire masse est nulle et le module
de limpdance dentre est inni. Lorsque , Z
E
m.
H. Djelouah
Variation de

X
1
en fonction de Variation de Z
E
= [Z
E
[ en fonction de
5.4 Application
Le phnomne dantirsonance peut tre avantageusement utilis pour supprimer une vibra-
tion rsultant dune rsonance dans un systme mcanique.
Etoueur de vibrations .
0,0 0,5 1,0 1,5 2,0 2,5 3,0
0
2
4
6
8
10
12
14

A
X
1
Variation de X
1
en fonction de .
Considrons le systme deux degrs de libert de la gure ci-dessus. Les quations di-
rentielles du mouvement scrivent
_
_
m x
1
+ x
1
+ (k +K) x
1
Kx
2
= F
Kx
1
+m x
2
+Kx
2
= 0
En rgime permanent sinusodal, on obtient
X
1
=
F
0
m
K
M
_
4
+
2
_
k+K
m
+
K
M
_
kK
mM
_
+i
K
M
_
X
2
=
KF
0
Mm
1
_
4
+
2
_
k+K
m
+
K
M
_
kK
mM
_
+i
K
M
_
H. Djelouah
5.4 Application 45
Lorsque la pulsation de la force excitatrice est gale
A
=
_
K
M
, la masse m est immobile
(X
1
= 0).
Si on choisit K et M telles que
k
m
=
K
M
(cest--dire telles que
0
=
A
), la masse m est
immobile lorsque la pulsation excitatrice est gale
0
=
_
k
m
=
_
K
M
. Dans ces conditions,
lajout de M et K permet dannuler la vibration de m cette pulsation. Un tel dispositif
constitue un toueur dynamique de vibrations.
Exercices
Exercice 1 : Dans la gure ci-dessous, M et R reprsentent respectivement la masse et le
rayon de la poulie, x
1
et x
2
les carts des deux masses par rapport leur position dquilibre.
On prend : M = 2(m
2
m
1
) avec m
2
= m et k
0
= k
1
= k
2
= k. Le systme sera tudi en
rgime permanent avec : F(t) = F
0
cos(t).

m
1
m
2
k
1
k
0
k
2
M
x
1
x
2
F(t)
1. Calculer limpdance dentre.
2. Calculer les vitesses x
1
(t) et x
2
(t).
3. (a) A quelle pulsation la masse m
1
reste-t-elle immobile ?
(b) Dans ce cas, quelle est lamplitude doscillation de la masse m
2
?
4. (a) A quelles pulsations, la vitesse de la masse m
1
est en phase avec la force F(t) ?
(b) En comparant ces pulsations celles calcules dans lexercice 4 du chapitre prcdent,
dduire le dphasage de x
2
par rapport F(t) pour chacune de ces pulsations.
Exercice 2 :
1. Etablir les quations direntielles rgissant le fonctionnement des systmes reprsents
par les gures 1 et 2.
2. Pour
=
_
5k/4m
1
+g/r et m
1
= m
2
pour la gure 1
et =
_
k
2
/m avec m = M/2 +m
2
pour la gure 2,
calculer en rgime permanent sinusodal :
(a) limpdance dentre,
(b) y
1
, y
2
, y
1
et y
2
.
H. Djelouah

F(t)
y
2
y
1
k
k
k
m
1
m
2
y
2
m
1
k
2
y
1
m
2
r/2
r/2
r/2
r/2
k
1
F(t)
R
M
figure 1 figure 2
a
a
Exercice 3 : Pour les systmes mcaniques des gures 1 et 2 et avec F(t) = F
0
cos(t) et
pour =
_
k
1
/m
1
, calculer :
1. Limpdance dentre ,
2. La puissance instantane fournie par le gnrateur mcanique et la puissance instantane
dissipe par le systme. Comparer et commenter.
3. La puissance moyenne fournie par le gnrateur mcanique et la puissance moyenne dissipe
par le systme. Comparer et commenter.

k
1
m
1
k
2 1
m
2
2
y
1
y
2
k
1
m
1
k
2
1
m
2
2
y
1
y
2
F(t)
F(t)
figure 1 figure 2
a
a
a
a
H. Djelouah
Chapitre 6
Gnralits sur les phnomnes de
propagation
6.1 Propagation une dimension
6.1.1 Equation de propagation
Dans les phnomnes vibratoires traits dans les chapitres prcdents, nous nous sommes
intresss des phnomnes ou des grandeurs physiques qui dpendaient dune seule variable,
le temps. Nous allons maintenant examiner toute une srie de phnomnes qui sont dcrits par
une fonction qui dpend la fois du temps t et dune variable despace, x par exemple.
Ces phnomnes sont rgis par une quation aux drives partielles, appele quation de
dAlembert ou quation donde ou encore quation de propagation une dimension de la forme :
2
s
x
2

1
V
2
2
s
t
2
= 0
dans laquelle V est une grandeur physique qui a les dimensions dune vitesse et sera appele
dans la suite vitesse de propagation.
6.1.2 Solution de lquation de propagation
Mthode de dAlembert
Pour rsoudre lquation des ondes une dimension, oprons le changement de variable
suivant :
= t
x
V
= t +
x
V
Calculons les drives partielles par rapport t et x, en fonction des drives partielles par
rapport et .
Sachant que :
t
=

t
= 1
et que
x
=
x
=
1
V
on obtient
H. Djelouah
48 Gnralits sur les phnomnes de propagation
s
t
=
s
t
+
s
t
=
s
+
s
s
x
=
s
x
+
s
x
=
1
V
_
s
_
En tenant compte de ces rsultats et sachant que
2
s
=

2
s
on obtient :
2
s
t
2
=

2
s
2
2

2
s
+

2
s
2
s
x
2
=
1
V
2
_
2
s
2
2

2
s
+

2
s
2
_
En remplaant dans lquation donde

2
s
t
2
et

2
s
x
2
par les expressions ci-dessus, on obtient lqua-
tion donde exprime en fonction des drives partielles par rapport aux variables et :
2
s
= 0
Cette dernire quation peut scrire
_
s
_
= 0
Un intgration par rapport donne :
s
= f ()
o f () est une fonction qui ne dpend que de (et pas de ). Enn une intgration par rapport
donne :
s (, ) = F () +G()
o F () , qui ne dpend que de , est une primitive de f (). La fonction G() est une fonction
qui ne dpend que de . En revenant aux variables x et t, on obtient la solution gnrale de
lquation des ondes une dimension :
s (x, t) = F
_
t
x
V
_
+G
_
t +
x
V
_
Les fonctions F
_
t
x
V
_
et G
_
t +
x
V
_
sont des fonctions dont la nature est xe par les conditions
aux frontires imposes la solution s (x, t).
H. Djelouah
6.1 Propagation une dimension 49
Proprits des solutions particulires F
_
t
x
V
_
et G
_
t +
x
V
_
Proprits de F
_
t
x
V
_
On tudie le cas de la solution particulire F
_
t
x
V
_
. Pour cela
on suppose que les conditions aux frontires sont telles que G
_
t +
x
V
_
est constamment nulle.
On considre linstant t
1
un point dabscisse x
1
. La valeur de la fonction s en ce point et cet
instant est s (x
1
, t
1
). On recherche un instant t
2
postrieur t
1
(t
2
> t
1
) la position x
2
dun
point pour lequel la valeur de s est la mme que la valeur quelle avait en x
1
linstant t
1
. Ce
problme est formul par lgalit suivante :
s (x
1
, t
1
) = s (x
2
, t
2
)
Ce qui se traduit par
F
_
t
1
x
1
V
_
= F
_
t
2
x
2
V
_
Cette quation est satisfaite si
t
1
x
1
V
= t
2
x
2
V
Do la valeur de x
2
:
x
2
= x
1
+V (t
2
t
1
)
Comme t
2
> t
1
, x
2
est suprieure x
1
et ces deux points sont distants de
x
2
x
1
= V (t
2
t
1
)
F
_
t
x
V
_
correspond une onde se propageant dans le sens des x croissants (Voir la gure
ci-dessous). F
_
t
x
V
_
est appele onde progressive et cette expression constituera dans la suite
la dnition dune onde progressive.
x1
x1
x2
x2
t=t
1
t=t
2
>t
1
Direction de
propagation
x2-x1=V(t2-t1)
x
x
Onde progressive dans le sens des x croissants : F
_
t
x
V
_
Proprits de G
_
t +
x
V
_
On tudie le cas de la solution particulire G
_
t +
x
V
_
. Pour cela
on suppose que les conditions aux frontires sont telles F
_
t
x
V
_
est constamment nulle. On
considre linstant t
1
un point dabscisse x
1
. La valeur de la fonction s en ce point et cet
instant est s (x
1
, t
1
). On recherche un instant t
2
postrieur t
1
(t
2
> t
1
) la position x
2
dun
point pour lequel la valeur de s est la mme que la valeur en x
1
linstant t
1
. Ce problme est
formul par lgalit suivante :
s (x
1
, t
1
) = s (x
2
, t
2
)
Ce qui se traduit par
G
_
t
1
+
x
1
V
_
= G
_
t
2
+
x
2
V
_
Cette quation est satisfaite si
t
1
+
x
1
V
= t
2
+
x
2
V
H. Djelouah
Do la valeur de x
2
:
x
2
= x
1
V (t
2
t
1
)
Comme t
2
> t
1
, x
2
est infrieure x
1
. Ces deux points sont distants de
x
1
x
2
= V (t
2
t
1
)
G
_
t +
x
V
_
correspond une onde se propageant dans le sens des x dcroissants (Voir la gure
ci-dessous).
x1
x1
x2
x2
t=t
1
t=t
2
>t
1
Direction de
propagation
x1-x2=V(t2-t1)
x
x
Onde progressive dans le sens des x dcroissants : G
_
t +
x
V
_
6.1.3 Onde progressive sinusodale
On considre une onde progressive se propageant dans la direction de laxe des x, telle que
le point dabscisse x = 0 est soumis une vibration sinusodale de la forme
s (x = 0, t) = S
0
cos (t)
Le point se trouvant labscisse x > 0 aura la mme vibration que celle du point x = 0 mais
avec un retard gal
x
V
:
s (x, t) = S
0
cos
_
_
t
x
V
__
Cette expression constitue la dnition dune onde progressive sinusodale (ou harmonique) ; elle
peut tre crite sous la forme :
s (x, t) = S
0
cos [t (x)]
o (x) =

V
x reprsente le dphasage li au temps de propagation
x
V
. On dit que (x) reprsente
le dphasage d la propagation. Londe progressive sinusodale scrit sous la forme suivante
qui permet de mettre en vidence la double priodicit (dans le temps et dans lespace) :
s (x, t) = S
0
cos
_
2
_
t
T

x
__
La quantit T =
2
est la priode temporelle tandis que la quantit = V T est la longueur

donde qui constitue la priode spatiale. On peut vrier aisment que :
s (x, t +nT) = s (x, t)
s (x +n, t) = s (x, t)
o n est un nombre entier.
H. Djelouah
Londe progressive scrit souvent :
s (x, t) = S
0
cos [t kx]
o k =

V
=
2
est appel le module du vecteur donde qui sexprime en m

1
.
On utilise trs souvent la notation complexe dune onde progressive sinusodale :
s (x, t) = S
0
e
i(tkx)
s (x, t) = S e
it
o S = S
0
e
ikx
reprsente lamplitude complexe de londe progressive sinusodale. Le module
S
0
de S est lamplitude de londe tandis que son argument kx reprsente le dphasage d la
propagation.
6.1.4 Superposition de deux ondes progressives sinusodales
Cas de deux ondes de mme frquence se propageant dans le mme sens
Considrons deux ondes de mme frquence et de mme direction de propagation, dampli-
tudes respectives S
1
et S
2
, et de phases respectives
1
et
2
. Londe rsultante sera alors :
s (x, t) = S
1
e
i(tkx+
1
)
+S
2
e
i(tkx+
2
)
= S e
i(tkx+)
ou encore en notation relle :
s (x, t) = S cos (t kx +)
avec
S =
_
S
2
1
+S
2
2
+ 2S
1
S
2
cos (
1
2
)
et
= Arctg
_
S
1
sin (
1
) +S
2
sin (
2
)
S
1
cos (
1
) +S
2
cos (
2
)
_
La superposition de deux ondes harmoniques de mme frquence, et qui se propagent dans la
mme direction, donne une autre onde harmonique progressive de mme frquence, damplitude
S et de phase .
Cas de deux ondes de mme frquence se propageant dans des sens opposs
Si par contre, on superpose deux ondes harmoniques de mme frquence mais se propageant
dans des sens opposs, le rsultat est tout autre. En eet, dans ce cas :
s (x, t) = S
1
e
i(tkx+
1
)
+S
2
e
i(t+kx+
2
)
=
_
S
1
e
i
1
e
ikx
+S
2
e
i
2
e
+ikx
_
e
it
et on ne peut plus crire londe rsultante sous la forme dune onde progressive simple. Un cas
particulier important se produit quand les deux amplitudes sont identiques. Si on note :
S
1
= S
2
= S
0
on a :
s (x, t) = 2S
0
cos
_
kx +

1
2
2
_
e
i
_
t+
1
+
2
2
_
H. Djelouah
et donc en notation relle :
s (x, t) = 2S
0
cos
_
kx +

1
2
2
_
cos
_
t +

1
+
2
2
_
Ce mode de vibration est trs dirent dune onde progressive puisque tous les points x de la
corde vibrent en phase avec des amplitudes direntes. En particulier, il existe une srie de
points :
x
n
=
__
n +
1
2
_
2
2
_

2
avec
n = 0, 1, 2,
o lamplitude de vibration est constamment nulle. On dit dans ce cas que londe est sta-
tionnaire et que les points x
n
sont les nuds de londe. Entre chaque paire de nuds existe un
ventre o lamplitude de vibration est maximum et gale 2S
0
. On note aussi que lintervalle
entre deux nuds est gal une demi-longueur donde /2.
6.1.5 Vitesse de phase
Considrons une onde progressive sinusoidale qui se propage dans le sens des x croissants.
Un point dabscisse x possde, linstant t, llongation :
s (x, t) = S
0
cos (t kx)
Entre linstant t et t + t londe progresse dune quantit x. A linstant t + t, le point
dabscisse x + x possde la mme longation que celle que possdait le point dabscisse x
linstant antrieur t. Ceci se traduit par lgalit :
s (x, t) = s (x + x, t + t)
S
0
cos (t kx) = S
0
cos [ (t + t) k (x + x)]
Cette galit est satisfaite si les phases instantanes sont gales :
t kx = (t + t) k (x + x)
Soit encore
t = k x
On dnit la vitesse de phase V
=
x
t
qui sexprime en fonction de et k par :
V
=

k
Si la vitesse de phase ne dpend pas de , le milieu est dit non dispersif. Dans le cas contraire
il est dit dispersif.
La gure ci-dessous permet dillustrer la notion de vitesse de phase en considrant deux
reprsentations des instants dirents dune corde parcourue par une onde . La courbe continue
reprsente lensemble des points de la corde linstant t. Le point de la corde dabscisse x est
reprsent par le point blanc, tandis que le point dabscisse x + x est reprsent par le point
noir. On constate quentre les instants t et t + t chacun de ces points suit une trajectoire
rectiligne et le dplacement du point noir linstant t + t est gal au dplacement du point
blanc linstant t. En particulier la crte de la corde, correspondant une valeur particulire
de la phase instantane, semble se dplacer dans le sens de propagation de londe avec la vitesse
de V
mais la trajectoire de chaque point matriel est une trajectoire rectiligne perpendiculaire
la direction de propagation.
H. Djelouah
t t+t
x
x
Onde progressive sinusodale
Trajectoire de deux points et entre les instants t et t + t
6.1.6 Vitesse de groupe
La vitesse de phase V
nest pas ncessairement la vitesse que lon observe lorsquon analyse

un mouvement ondulatoire. En gnral une onde nest pas parfaitement sinusodale mais a une
dure limite et se prsente sous la forme dun train donde appel communment pulse ou
groupe qui se propage avec une vitesse V
G
appele vitesse de groupe. Cette onde sous la forme
dun pulse contient plusieurs frquences. Si la vitesse de phase est indpendante de la frquence
(Milieu non dispersif) alors toutes les frquences qui constituent le pulse se propagent la mme
vitesse et le pulse se propage avec une vitesse de groupe gale la vitesse de phase. Mais si le
milieu est dispersif (i.e. la vitesse de phase dpend de la frquence), alors le pulse se propage
avec une vitesse de groupe dirente de la vitesse de phase.
Pour illustrer ce phnomne, considrons une onde constitue de deux ondes de frquences
direntes et de mme amplitude. En x = 0, cette onde scrit par exemple sous la forme :
s (0, t) = S
0
cos (
1
t) +S
0
cos (
2
t)
Cette onde peut scrire encore :
s (0, t) = 2S
0
cos (
B
t) cos (t)
o
B
=

2
1
2
et =

2
+
1
2
Si
1
est voisine de
2
, la vibration rsultante se prsente sous la forme dune sinusode de
pulsation dont lamplitude est module par un battement de pulsation
B
(Modulation dam-
plitude).
En un point x > 0, londe obtenue rsulte de la superposition de ces deux ondes qui se sont
propages des vitesses direntes car le milieu de propagation est suppos dispersif :
s (x, t) = S
0
cos (
1
t k
1
x) +S
0
cos (
2
t k
2
x)
s (x, t) peut scrire :
s (x, t) = 2S
0
cos (
B
t k
B
x) cos (t kx)
Dans cette expression :
k
B
=
k
2
k
1
2
et k =
k
2
+k
1
2
H. Djelouah
Lamplitude du battement se propage une vitesse qui est la vitesse de groupe dnie par la
relation :
V
G
=

B
k
B
=

2
1
k
2
k
1
Comme k
2
est peu dirent de k
1
, la vitesse de groupe est dnie par :
V
G
= lim
k
2
k
1
1
k
2
k
1
=
d
dk
Tandis que la sinusode contenue lintrieur du battement se propage la vitesse de phase :
V
=

k
Propagation dun paquet dondes : Les ches verticales noires correspondent au maximum des
battements qui se propagent la vitesse de groupe. Les ches verticales blanches
correspondent au maximum des vibrations qui se propagent la vitesse de phase.
6.1.7 Onde vectorielle
Dans ce qui prcde, la quantit s (x, t) reprsente une grandeur scalaire, mais certains ph-
nomnes dcrits par des vecteurs conduisent des quations similaires :
2

A
x
2

1
V
2
2

A
t
2
= 0
Le vecteur

A, dni dans un milieu trois dimensions, possde trois composantes A
x
, A
y
,
A
z
et lexpression ci-dessus signie que chacune de ces composantes satisfait individuellement
lquation de propagation :
_
2
A
x
x
2

1
V
2

2
A
x
t
2
= 0
2
A
y
x
2

1
V
2
A
y
t
2
= 0
2
A
z
x
2

1
V
2

2
A
z
t
2
= 0
Chacune de ces composantes A
x
, A
y
, A
z
se propage en t
x
V
et t +
x
V
.
H. Djelouah
6.2 Propagation dans lespace trois dimensions 55
6.2 Propagation dans lespace trois dimensions
Dans un systme de coordonnes cartsiennes, lquation de propagation dans lespace trois
dimensions scrit sous la forme :
2
s
x
2
+

2
s
y
2
+

2
s
x
2

1
V
2
2
s
t
2
= 0
On dnit le laplacien scalaire de s par lexpression ci-dessous :
s =

2
s
x
2
+

2
s
y
2
+

2
s
x
2
et lquation des ondes scrit sous la forme condense :
s
1
V
2
2
s
t
2
= 0
s est fonction du temps mais galement des cordonnes du point M o la fonction s doit tre
calcule. Si lon appelle le vecteur position r =
OM, la quantit s dpend du temps et du vecteur

position r ; on crit s (r, t).
6.2.2 Onde plane progressive sinusodale
Dnition
Londe progressive sinusodale (ou harmonique), se propageant dans une direction donne
par un vecteur unitaire u est dnie par :
s (r, t) = S
0
cos
_
t
k r
_
o le vecteur

k = k u est appel le vecteur donde. Si les composantes du vecteur

k sont k
x
, k
y
et k
z
, alors londe plane est dnie par
s (x, y, z, t) = S
0
cos (t k
x
x k
y
y k
z
z)
On peut utiliser la notation complexe pour reprsenter londe plane progressive sinusodale qui
scrit dans ce cas sous la forme :
s (r, t) = S
0
e
i(t
kr)
Relation de dispersion
En remplaant s(r, t) par son expression dans lquation de propagation, on obtient la relation
k = k () qui est la condition pour que londe plane dnie ci-dessus constitue une solution
particulire de lquation donde. Cette relation est appele la relation de dispersion et elle
scrit :
k =

V
H. Djelouah
Surface donde
On appelle surface donde ou surface quiphase, lensemble des points de lespace pour les-
quels, au mme instant, s (r, t) a la mme valeur. Recherchons la surface donde passant par
un point M
0
un instant t ; cette surface est lensemble des points M de lespace pour lesquels
lgalit suivante est satisfaite :
s (r, t) = s (r
0
, t)
Cette galit se traduit par :
S
0
e
i(t
kr)
= S
0
e
i(t
kr
0)
Cette galit est satisfaite si
k r =
k r
0
Tenant compte des proprits du produit scalaire, on obtient
k (r r
0
) = 0
La surface donde passant, linstant t, par le point M
0
est lensemble des points M satisfaisant
lquation ci-dessus. Cette surface est un plan passant par M
0
, et perpendiculaire la direction
du vecteur donde, donc la direction de propagation. Londe est dite plane.
y
x
z M
0
M
u
r
k
r
r
r
0
r
r
Surface donde
Direction de
propagation
Onde plane
Il existe dautres types dondes dnis par les surfaces donde respectives : par exemple les
ondes sphriques pour lesquelles les surfaces donde sont des sphres ou les ondes cylindriques
pour lesquelles les surfaces donde sont des cylindres.
Polarisation
Dans le cas dune onde plane progressive sinusodale reprsente par une quantit vectorielle
A(r, t), cette quantit peut avoir direntes orientations par rapport aux surfaces dondes :
1.

A est constamment perpendiculaire la surface donde, ou de manire quivalente parallle
la direction de propagation : londe est dite longitudinale.
2.

A est contenu dans la surface donde, ou de manire quivalente perpendiculaire la di-
rection de propagation : londe est dite transversale. Dans ce cas, lextrmit du champ
vectoriel

A peut dcrire une trajectoire rectiligne : londe transversale est dite polarisa-
tion rectiligne. Elle peut dcrire une trajectoire circulaire (onde transversale polarisation
circulaire), ou une trajectoire elliptique (onde transversale polarisation elliptique).
H. Djelouah
6.2 Propagation dans lespace trois dimensions 57
Exercices
Exercice 1 : Vrier que les fonctions suivantes :
1. u(x, t) = Asin
_
_
t
x
V
__
2. u(x, t) = Acos (k (x V t))
3. u(x, t) = (x +V t)
2
4. u(x, t) = Aexp
_
i
_
t
x
V
__
5. u(x, t) = Aexp
_
i
_
t +
x
V
__
6. u(x, t) = Aexp
_
i
_
t
x
V
__
+Bexp
_
i
_
t +
x
V
__
sont solutions de lquation :
2
u
x
2

1
V
2
2
u
t
2
= 0
o x, t et V reprsentent respectivement la position, le temps et la vitesse de propagation.
Dterminer les dimensions des constantes A, , k et .
Exercice 2 : On tudie la propagation dun branlement transversal sur une corde. Cet bran-
lement se propage dans le sens des x croissants avec une vitesse V . A linstant t = 0 s, la forme
de la corde est donne par : u(x, 0) = Ae
x
2
. Donner lexpression de la forme u(x, t) de la
corde un instant t. Reprsenter graphiquement cette corde aux instants t = 0 s, et t = 0.3 s
pour : A = 1 cm, = 0.5 cm
2
, V = 20 cm.s
1
.
Exercice 3 : Le dispositif reprsent sur la gure ci-dessous permet de communiquer lex-
trmit S dune corde tendue horizontalement, une vibration verticale sinusodale entretenue :
u(0, t) = 5 sin (t) (en cm)

Moteur
S
u(0,t)
Feutre
Poulie
M
L
1. La longueur totale de la corde est L = 5 m et sa masse est m = 100 g. Sachant que
la vitesse de propagation des ondes transversales dans une corde de masse linique et
tendue par une tension T est donne par : V =
_
T/, quelle doit tre la valeur de la
masse M qui tend la corde pour que la longueur donde des vibrations transversales de
pulsation soit = 1 m lorsque le moteur tourne la vitesse de 3600 tr/mn.
2. Juste avant la poulie, la corde est presse frottement doux entre deux plaques de feutre,
empchant toute rexion de se produire.
(a) Ecrire lexpression en fonction du temps de llongation u(x, t) du point A tel que
SA = x.
(b) Donner les abscisses des points qui vibrent en phase avec S et de ceux qui vibrent en
opposition de phase avec S.
(c) Reprsenter sur un mme graphique le mouvement de S entre les instants t = 0 et
t = 1/30 s et le mouvement du point A tel que x = 2, 75 m.
(d) Reprsenter laspect de la corde sur un mme graphique aux instants t = 0 et t =
1/600 s, entre x = 0 et x = 4 m.
H. Djelouah
H. Djelouah
Chapitre 7
Cordes vibrantes
7.1 Equation des ondes
Considrons une corde tendue, rectiligne selon la coordonne x, et de longueur innie. Nous
allons tudier la propagation dun faible branlement le long de la corde. Supposons que cet
branlement se produise suivant laxe 0y.
Etudions lquation du mouvement de cette corde. Nous dnoterons par T la tension
laquelle est soumise la corde. On considre en un point dabscisse x un segment trs court de
cette corde, de longueur x. La masse m du segment est donne par :
m = x
o est la densit linique de masse de la corde, cest--dire la masse par unit de longueur
qui sexprime en kg/m.
lquilibre
en mouvement
x
y
x x+x
x
u
y
(x,t)
T(x+x)
(x+x)
(x)
T(x)
F
y
(x+x)
F
y
(x)
Corde vibrant transversalement.
Dans une situation hors quilibre, le segment nest plus droit, il prsente une courbure. Nous
considrons des mouvements doscillation de la corde de petite amplitude
u(x, t) = u(x, t) e
y
si bien que nous pouvons faire lapproximation :
sin ()[
x
= tan ()[
x
=
u
x
x
sin ()[
x+x
= tan ()[
x+x
=
u
x
x+x
H. Djelouah
60 Cordes vibrantes
Cette approximation nglige aussi lallongement du segment, et considre donc la tension T
comme constante. La force applique sur le segment dans la direction y est la rsultante de la
force applique au point x, qui est une force applique vers le bas et gale en module
F (x, t) = T sin ()[
x
= T tan ()[
x
= T
u
x
x
et de la force applique au point x+x qui est vers le haut et gale
F (x + x, t) = T sin ()[
x+x
= T tan ()[
x+x
= T
u
x
x+x
La force totale dans la direction y est donc :
R = F (x + x, t) F (x, t) = T
_
u
x
x+x
u
x
x
_
= T

2
u
x
2
x
Nous pouvons appliquer maintenant la loi fondamentale de la dynamique au segment x. La
force dans la direction y doit tre gale au produit de la masse m du segment par lacclration
de celui-ci. Donc :
R = m

2
u
t
2

2
u
t
2
= T

2
u
x
2
Si on dnit V =
_
T
qui a la dimension dune vitesse, on constate que :
2
u
x
2

1
V
2
2
u
t
2
= 0
qui est lquation donde de la corde. V est la vitesse de propagation de cette onde.
7.2 Ondes progressives harmoniques
7.2.1 Dnition
Une onde progressive harmonique se propageant selon Ox est dnie par :
u(x, t) = U
0
cos (t kx)
ou encore en notation complexe
u(x, t) = U
0
e
i(tkx)
o k =

V
=
2
est le module du vecteur donde, tant la longueur donde.

7.2.2 Force en un point
On appelle force en un point, la projection selon Oy de la force exerce, en ce point, par la
partie gauche de la corde sur la partie droite :
F = T
u
x
Dans le cas dune onde progressive sinusodale, cette relation devient :
F(x, t) = ikT U
0
e
i(tkx)
H. Djelouah
7.3 Oscillations libres dune corde de longueur nie 61
La vitesse de particules scrit :
u(x, t) =
u
t
= i U
0
e
i(tkx)
On constate que pour une onde progressive la vitesse de particules u est en phase avec la
force F.
7.2.3 Impdance
On appelle impdance en un point le rapport de lamplitude complexe de la force lampli-
tude complexe de la vitesse de particule
Z (x) =
F
y
u
y
Dans le cas dune onde progressive, on obtient :
Z (x) = V =
_
T
La quantit

T dnit limpdance caractristique de la corde
Z
c
=
_
T = V
On obtient une proprit de londe progressive plane
Z (x) = Z
c
x
7.3 Oscillations libres dune corde de longueur nie
x
T,
y
u(x,t)
L
Corde de longueur L xe aux extrmits
Considrons une corde de longueur L xe aux points x = 0 et x = L. Recherchons une
solution de lquation donde sous la forme :
u(x, t) = g (x) f (t)
En remplaant dans lquation de propagation, on obtient :
1
g
d
2
g
dx
2
=
1
V
2
1
f
d
2
f
dt
2
Le membre de gauche de cette quation ne dpend que de x, tandis que le membre de droite
ne dpend que de t. Ces deux expressions sont donc gales une constante qui doit tre un
nombre rel ngatif que nous posons gal k
2
car la solution ne doit pas tendre vers linni
lorsque t tend vers linni. Posons = k V . On en dduit que :
H. Djelouah
62 Cordes vibrantes
d
2
g
dx
2
= k
2
g
d
2
f
dt
2
=
2
f
Les solutions de ces deux quations direntielles sont de la forme :
f = A cos (t) +B sin (t)
g = C cos (kx) +Dsin (kx)
La solution de lquation donde peut alors scrire sous la forme :
u(x, t) = [A cos (t) +B sin (t)] [C cos (kx) +D sin (kx)]
Tenant compte des conditions aux limites
u(0, t) = 0
u(L, t) = 0
on obtient
C = 0
k = n

L
o n = 0, 1, 2,
La solution de lquation donde qui satisfait ces conditions aux limites est donc la somme
dune innit de termes :
u(x, t) =
n=0
[a
n
cos (
n
t) +b
n
sin (
n
t)] sin (k
n
x)
avec
k
n
= n
L
et
n
= k
n
V = n
V
L
Les
n
sont les pulsations propres. Les coecients a
n
et b
n
sont dtermins par les conditions
initiales du mouvement. Supposons qu t = 0 nous imposions la corde une certaine forme
initiale u(x, 0) = u
0
(x) et une vitesse initiale
u(0, x) = v
0
(x)
Dans ce cas nous aurons les conditions initiales suivantes :
u
0
(x) =

n=0
a
n
sin (k
n
x)
v
0
(x) =

n=0
n
b
n
sin (k
n
x)
On doit inverser ces quations pour obtenir les coecients a
n
et b
n
. La mthode de Fourier
consiste les multiplier par sin (k
m
x) et les intgrer entre 0 et L. Si on utilise les intgrales :
_
L
0
sin
_
m
x
L
_
sin
_
n
x
L
_
dx =
_
_
_
0 si m ,= n
L
2
si m = n
on obtient
H. Djelouah
7.4 Rexion et transmission 63
a
n
=
2
L
_
L
0
u
0
(x) sin
_
n
x
L
_
dx
b
n
=
2
n
L
_
L
0
v
0
(x) sin
_
n
x
L
_
dx
7.4 Rexion et transmission
7.4.1 Rexion et transmission entre deux cordes semi-innies
incidente rflchie
transmise
x
y
T,
1
T Z
T
V
1 1
1
1
=
=
T,
2
T Z
T
V
2 2
2
2
=
=
0
Rexion transmission dans deux cordes semi-innies
Soit deux cordes de longueur semi-innie, relies en x = 0. Leurs masses liniques sont
respectivement
1
et
2
. Lorsquune onde venant de se propage vers x = 0 dans la premire
corde, elle donne naissance au point de jonction, x = 0, une onde rchie et une onde
transmise. Lcriture de la continuit du dplacement et de la force en x = 0 permet dobtenir
le coecient de rexion R
u
et le coecient de transmission T
u
dnis respectivement par :
R
u
=
U
R
U
i
T
u
=
U
T
U
i
o U
i
, U
R
et U
T
sont les amplitudes des dplacements associs respectivement londe
incidente, londe rchie et londe transmise. On en dduit :
R
u
=
Z
1
Z
2
Z
1
+Z
2
T
u
=
2Z
1
Z
1
+Z
2
7.4.2 Rexion sur une impdance quelconque
Z
T
T,
T Z
T
V
C

=
=
x 0
Corde semi-innie termine par une impdance Z
T
H. Djelouah
64 Cordes vibrantes
Soit une corde de longueur semi-innie, de masse linique , tendue horizontalement avec une
tension T et termine en x = 0 par une impdance mcanique Z
T
. Lorsquune onde harmonique
se propage dans la corde de vers x = 0, elle subit une rexion en ce point. Sachant que le
dplacement de particules scrit :
u(x, t) = U
i
e
i(tkx)
+U
R
e
i(t+kx)
on en dduit la vitesse de particules et la force en un point dabscisse x
u =
u
t
= i
_
U
i
e
i(tkx)
+U
R
e
i(t+kx)
_
F = T
u
x
= ikT
_
U
i
e
i(tkx)
U
R
e
i(t+kx)
_
En x = 0, les conditions aux limites scrivent :
Z
T
=
F(0, t)
u(0, t)
On en dduit le coecient de rexion R
u
en fonction de limpdance caractristique Z
c
et
de limpdance Z
T
place lextrmit de la corde :
R
u
=
U
R
U
i
=
Z
c
Z
T
Z
c
+Z
T
Exercices
Exercice 1 : Soit une corde de longueur L = 2 m, de masse totale m = 80 g et soumise
une tension T rglable. Comme indiqu sur la gure ci-dessous, elle est xe en A, un
ressort vertical de raideur K dont lextrmit C subit un dplacement forc vertical sinusoidal
de frquence f = 50 Hz, damplitude s
0
= 1 cm et dcrit par : s(t) = s
0
e
i2ft
La seconde extrmit B(x = L) de la corde est xe un amortisseur de coecient de
frottement visqueux gal 0, 2 N.s/m. Des guides parfaitement glissants nautorisent que
les mouvements verticaux (transverses) des points A, B et C. Le mouvement dun point M
quelconque dabscisse x sur la corde est alors reprsent par son longation u
y
(x, t) . La tension
T est rgle de telle sorte quil ny ait pas donde rchie en B.

B
L
K
C
A
O
s(t)
x
a
y
1. Que reprsente lamortisseur par rapport la corde ? Calculer limpdance en un point
quelconque de la corde. En dduire la tension T de la corde.
2. En dduire la vitesse de phase V et la longueur donde .
3. Montrer que les extrmits A et B vibrent en phase.
H. Djelouah
7.4 Rexion et transmission 65
4. Quelle est la valeur de limpdance de la corde au point A. Calculer lamplitude et la phase
de llongation u
y
(x, t) du point A. En dduire lexpression de llongation u
y
(x, t) dun
point quelconque de la corde. Dans quel cas la phase est nulle ? Que vaut, dans ce cas,
lamplitude de vibration de chaque point de la corde ?
Exercice 2 : Soit deux cordes de longueur semi-innie relies en x = 0. La corde qui stend
de 0 a une densit linique
1
. La seconde corde qui stend de 0 + a une densit
linique
2
= 0.25
1
. Lorsquune onde incidente sinusodale se propage de dans le sens des
x positifs, elle subit une rexion partielle en x = 0. Lamplitude de londe incidente est U
0
et
sa pulsation est .
1. Calculer le coecient de rexion en x = 0.
2. Montrer que londe rsultante dans la premire corde a une amplitude qui varie entre deux
valeurs extrmes U
max
et U
min
.
(a) Donner lexpression de U
max
en fonction de U
0
et calculer la position des maxima en
fonction de la longueur donde .
(b) Donner lexpression de U
min
en fonction de U
0
et calculer la position des minima en
fonction de la longueur donde .
(c) Calculer le taux dondes stationnaires.
Exercice 3 : Une corde de longueur L est tendue entre deux points situs respectivement en
x = 0 et x = L. Le point situ en x = 0 est xe et le point situ en x = L est reli un ressort
de raideur K. La tension de la corde est T. La corde est horizontale lquilibre et on pourra
ngliger son poids. On tudie les ondes transverses stationnaires sinusodales de pulsation . La
vitesse de propagation est V .

x
L
y
K
1. Ecrire le dplacement u
y
(x, t) en un point quelconque dabscisse x et linstant t.
2. En crivant la condition limite pour x = 0, montrer que u
y
(x, t) peut se mettre sous la
forme : u
y
(x, t) = Ae
it
f (x) ; o f(x) est une fonction que lon explicitera.
3. Ecrire la condition aux limites en x = L.
4. Montrer que les pulsations propres doivent vrier la condition : tg
_
L
V
_
= C
L
V
o C est
une constante que lon prcisera. Proposer une mthode de rsolution de cette quation.
5. Dterminer les trois premires pulsations propres
1
,
2
et
3
dans le cas o
T
KL
.
Exercice 4 : On considre une corde homogne de masse par unit de longueur tendue
horizontalement avec une tension T trs grande devant le poids de la corde.. La corde de longueur
innie est termine en x = 0 par un amortisseur de coecient de frottement visqueux . Une
onde incidente transversale arrive de et se propage dans la corde dans le sens des x croissants.
Cette onde correspond un dplacement transversal donn par :
u
i
(x, t) =
Ui
e
i(tkx)
o k reprsente le module du vecteur donde.
H. Djelouah
66 Cordes vibrantes
y
x
0
a
1. Donner lexpression du coecient de rexion R en amplitude de dplacement en x = 0.
Quel est le module et largument de R dans le cas particulier o
T ?
2. Ecrire lexpression du dplacement rsultant u(x, t), en chaque point de la corde, en fonc-
tion des donnes du problme et du coecient de rexion R.
3. Montrer que le dplacement rsultant en chaque point de la corde peut alors scrire sous
la forme de la somme dune onde progressive et dune onde stationnaire et quil scrit sous
la forme :
u(x, t) =
Up
e
i(t kx)
+ U(x) e
it
U
p
et U(x) sont deux nombres rels qui reprsentent respectivement lamplitude de londe
progressive et lamplitude de londe stationnaire. Calculer lamplitude U
p
en fonction de
R et U
i
, ainsi que lamplitude U(x) en fonction de R, U
i
, k et x.
4. Que devient u(x, t) dans les cas particuliers suivants :
(a) =
T,
(b) = 0.
Exercice 5 : Une corde de longueur L et de masse m est tendue entre deux points xes avec une
tension T. A linstant t = 0, la corde est pince en son milieu, carte par rapport lhorizontale
dune distance h puis lche sans vitesse initiale. Les positions u(x, 0) des dirents points de la
corde, linstant t = 0, sont reprsentes sur la gure ci-dessous. Etablir lexpression de u(x, t).
x

y
0
L/2
L
h
H. Djelouah
Chapitre 8
Ondes lastiques dans les solides
8.1 Proprits lastiques des solides
8.1.1 Dformation
Allongement dun barreau sous laction dune force de traction.
Soit un solide dformable, continu et isotrope, sous la forme dun barreau rectiligne de faible
section, cestdire dont les dimensions latrales sont faibles devant sa longueur , dont une
extrmit est xe sur un support rigide xe. Sous laction dune force de traction F applique
lextrmit libre, le l sallonge. La dformation persiste tant que la traction est maintenue.
Lallongement relatif est :
est la longueur du barreau dform. Chaque partie du barreau nest pas ncessairement
dforme de la mme manire. Il faut donc dnir un allongement relatif local, cestdire qui
dpend de la position en chaque point dabscisse x.
Dformation locale dun barreau.
Pour cela, considrons la portion du barreau situe initialement entre les points dabscisses
respectives x et x+x. Lorsque la traction est exerce, ces points se dplacent et leurs abscisses
H. Djelouah
68 Ondes lastiques dans les solides
respectives deviennent x +u
x
(x) et x + x +u
x
(x + x). Lpaisseur de llment situ entre
les deux sections devient :
x
= [x + x +u
x
(x + x)] [x +u
x
(x)]
Si lpaisseur x est susamment petite, un dveloppement en srie de Taylor au premier
ordre permet dcrire :
u
x
(x + x) = u
x
(x) +
u
x
x
x
Lallongement relatif de llment est :
x
x
x
=
u
x
(x + x) u
x
(x)
x
Par dnition, la dformation au voisinage du point dabscisse initiale x est la limite de ce
rapport lorsque x tend vers zro, cest--dire la drive de u
x
par rapport x :
= lim
x0
u
x
(x + x) u
x
(x)
x
=
u
x
Il convient de noter que la dformation qui est le rapport de deux longueurs est sans
dimension. Lorsque est ngative on dit que le milieu subit une contraction locale et si est
positive le milieu subit une extension locale.
8.1.2 Contrainte moyenne
Le l sest allong sous leet de la force extrieure F exerce normalement sur sa section
droite de surface S. Dans le cas gnral, cette force nest pas constante le long du l, elle dpend
de labscisse x. On dnit la contrainte moyenne par le rapport :
=
F
S
Cette grandeur homogne une force par unit de surface sexprime en N m
2
(ou en Pa).
8.1.3 Loi de Hooke
Dans le domaine de llasticit linaire, cest--dire pour des tensions mcaniques et des
dformations pas trop importantes, la dformation est proportionnelle la contrainte. Cette
proprit est exprime par la loi de Hooke :
=
1
E
F
S
=
1
E
ou de manire quivalente
=
F
S
= E
Dans cette expression la constante E, caractristique du matriau constituant le l, sappelle
le module dYoung ; elle a les dimensions dune force par unit de surface (en N m
2
ou en Pa).
8.1.4 Coecient de Poisson
En plus de lallongement selon Ox, il se produit un rtrcissement dans les directions per-
pendiculaires laxe du l. Si d est la dimension latrale du l, on a :
d
d
=
d
d
d
=

Le coecient est appel coecient de Poisson; cest un nombre positif toujours infrieur
0.5. Pour les mtaux usuels, sa valeur est = 0.3.
H. Djelouah
8.2 Onde plane longitudinale 69
8.1.5 Loi de Hooke pour les forces tangentielles
Barreau soumis une force de cisaillement.
Si nous appliquons la surface S dun barreau une force F, non plus normale mais tangen-
tielle, la longueur du barreau ne change pas, seules les artes normales au plan dapplication de
F tournent dun angle .
Dans lapproximation de llasticit linaire (cas des petites valeurs de ), langle est
proportionnel la force applique. La loi de Hooke sexprime dans ce cas par :
F
S
= G G tan () = G
h
o G est le module de cisaillement ; il sexprime galement en N m

2
.
Le tableau ci-dessous donne les valeurs caractristiques des modules de quelques matriaux
courants.
Matire ( kg m
3
) E ( N m
2
) G ( N m
2
)
Acier 7.810
3
2.210
11
0.910
11
Fer 7.8510
3
210
11
0.810
11
Aluminium 2.710
3
0.710
11
0.2610
11
Cuivre 8.9310
3
1.2210
11
0.4210
11
Caractristiques mcaniques de quelques mtaux usuels.
8.2 Onde plane longitudinale
Nous allons considrer ici uniquement le cas des ondes planes longitudinales se propageant
dans un barreau. Considrons un lment du barreau de section S compris entre deux sections
dabscisses respectives x et x + x. La section dabscisse x est soumise une traction F (x) de
la part de la partie gauche du barreau, tandis que la section dabscisse x+x est soumise une
traction F (x + x) de la part de la partie droite du barreau. Sous laction de ces deux forces
les deux sections se dplacent respectivement de u
x
(x) et u
x
(x + x) le long de laxe (Ox). Le
dplacement de particules u
x
est une fonction la fois de la coordonne x et du temps t. Si
est la masse volumique du barreau, la masse de llment dpaisseur x scrit :
m = S x
H. Djelouah
crivons la relation fondamentale de la dynamique pour cet lment :
S x

2
u
x
t
2
= F (x +dx) F (x)
Dans le cas o x est faible, la force F (x + x) agissant en x + x scrit :
F (x + x) = F (x) +
F
x
x
et la relation fondamentale de la dynamique devient
S x

2
u
x
x
2
=
F
x
x
Sachant que la force normale F est relie la dformation =
u
x
x
par la loi de Hooke :
F = SE = SE
u
x
x
on obtient
2
u
x
x
2

E
2
u
x
t
2
= 0
On retrouve lquation des ondes (quation de dAlembert) qui dcrit la propagation dun
branlement la vitesse
V =
Les ondes dcrites par cette quations correspondent une grandeur physique vectorielle,
le dplacement de particules u , oriente le long de la direction de propagation. Ce type de
mouvement ondulatoire est dit longitudinal.
8.2.2 Ondes progressives harmoniques
Dnition
Dans le cas dune onde progressive sinusodale, le dplacement de particules scrit en nota-
tion complexe :
u
x
(x, t) = U
0
e
i(tkx)
o k =

V
=
2
est le module du vecteur donde, tant la longueur donde.

La composante F
x
de la force exerce en x par la partie gauche sur la partie droite est
F
x
(x, t) = SE
u
x
x
= ikE u
x
(x, t) = ikEU
0
e
i(tkx)
Impdance
On appelle impdance en un point le rapport de lamplitude complexe de la force F
x

lamplitude complexe de la vitesse de particule u
x
:
Z (x) =
F
x
u
x
Dans le cas dune onde progressive harmonique, on a :
u
x
=
u
x
t
= i u
x
(x, t)
H. Djelouah
do lexpression de limpdance en un point
Z (x) = SV = S
_
E
On appelle impdance caractristique du milieu constituant le barreau, la quantit
Z
c
=
_
E = V
Do lexpression de limpdance mcanique du barreau :
Z (x) = SZ
c
Nous remarquons que limpdance caractristique ne dpend pas de la position; cette pro-
prit est caractristique des ondes planes progressives. Dans les autres cas, en prsence de
rexion par exemple, limpdance en un point dpend de la coordonne x. Notons que limp-
dance caractristique du milieu Z
C
sexprime en N m
2
tandis que limpdance Z du barreau
sexprime en kg s
1
.
8.2.3 Rexion et transmission
Rexion et transmission entre deux barreaux semi-innis
Soit deux barreaux de mme section S et de longueur semi-innie, relis en x = 0. Leurs
masses volumiques sont respectivement
1
et
2
. Lorsquune onde longitudinale venant de
se propage vers x = 0 dans le premier barreau , elle donne naissance au point de jonction, x = 0,
une onde rchie et une onde transmise. Lcriture de la continuit du dplacement et de la
contrainte mcanique en x = 0 permet dobtenir le coecient de rexion R
u
et le coecient de
transmission T
u
dnis respectivement par :
R
u
=
U
R
U
i
T
u
=
U
T
U
i
o U
i
, U
R
et U
T
sont les amplitudes des dplacements associs respectivement londe
incidente, londe rchie et londe transmise. On en dduit :
R
u
=
Z
1
Z
2
Z
1
+Z
2
T
u
=
2Z
1
Z
1
+Z
2
o Z
1
et Z
2
sont les impdances respectives du premier et du deuxime barreau.
Rexion lextrmit dun barreau termin par une masse M.
Considrons un barreau (, S, E) de longueur suppose semi-innie (x 0) termin en son
extrmit x = L par une masse M. Le barreau est le sige de la propagation dun onde incidente
et dune onde rchie ; londe rsultante scrit :
u(x, t) = U
i
e
i(tkx)
+U
R
e
i(t+kx)
crivons la relation fondamentale de la dynamique pour la masse M :
M

2
u
t
2
x=L
= ES
u
x
x=L
H. Djelouah
On en dduit lexpression du coecient de rexion au niveau de la masse M :
R
u
=
U
R
U
i
x=0
=
E i
M
S
E +i
M
S
On constate que le module du coecient de rexion [R
u
[ est gal 1 ; il sagit donc dun
phnomne de rexion totale. On retrouve un rsultat assez gnral qui est que le coecient
de rexion est gal la dirence des impdances sur la somme des impdances et que dans le
cas o limpdance terminale est imaginaire, il se produit un phnomne de rexion totale.
8.2.4 Oscillations libres dun barreau
Considrons un barreau de longueur L dont lune des extrmits (x = L) est libre et lautre
(x = 0) est xe un bti rigide . Lorsque le barreau est soumis une dformation longitudinale
initiale, il est le sige dondes longitudinales se propageant dans le sens des x croissant et des x
dcroissants. Chacune de ces ondes subit une rexion totale aux extrmits du barreau, donnant
ainsi une multitude donde se propageant dans les deux sens. Ces direntes ondes interfrent
entre elles.
Oscillations libres dun barreau
Pour ces raisons, nous recherchons une solution de lquation donde sous la forme :
u
x
(x, t) = A e
i(tkx)
+B e
i(t+kx)
Dans cette dernire expression le vecteur donde k est donn par la relation de dispersion
k =

V
tandis que A et B sont deux nombres complexes qui reprsentent lamplitude complexe
rsultante de toutes les ondes se propageant respectivement dans le sens des x croissant et dans
le sens des x dcroissant. Ces deux nombres complexes dpendent des conditions aux limites en
x = 0 et x = L , qui sont traduites par les quations suivantes :
_
u
x
(x = 0) = 0
F (x = L) = SE
u
x
x
x=L
= 0
La premire condition impose
A+B = 0
do B = A, et
u
x
(x, t) = A
_
e
ikx
e
+ikx
_
e
it
= 2iAsin (kx) e
it
La seconde condition impose
2ikSEA cos (kL) e
it
= 0
H. Djelouah
soit
cos (kL) = 0
dont les racines sont :
k
n
= (2n + 1)

2L
n tant un nombre entier. Les pulsations correspondantes permettant de satisfaire les conditions
aux frontires sont
n
= k
n
V = (2n + 1)
V
2L
Ces pulsations "permises" sont appeles les pulsations propres. Il y a donc une innit de
pulsations propres et la solution gnrale scrit :
u
x
(x, t) =
n=0
2iA
n
sin (k
n
x) e
i
n
t
En revenant la notation relle, cest--dire en prenant la partie relle de lexpression pr-
cdente, on obtient :
u
x
(x, t) =
n=0
[a
n
cos (
n
) +b
n
sin (
n
t)] sin (k
n
x)
o les coecients a
n
et b
n
sont relis aux nombres complexes A
n
par : 2iA
n
= a
n
ib
n
avec
k
n
= (2n + 1)

2L
et
n
= k
n
V = (2n + 1)
V
2L
Les
n
sont les pulsations propres. Les coecients a
n
et b
n
sont dtermins par les conditions
initiales du mouvement. Supposons qu t = 0 nous imposions aux dirents points du barreau
un dplacement initial
u(x, 0) = u
0
(x)
et une vitesse initiale
u(0, t) = v
0
(t)
Dans ce cas nous aurons les conditions initiales suivantes :
u
0
(x) =

n=0
a
n
sin (k
n
x)
v
0
(x) =

n=0
n
b
n
sin (k
n
x)
On doit inverser ces quations pour obtenir les coecients a
n
et b
n
. La mthode de Fourier
dcrite dans le chapitre prcdent, permet dobtenir :
a
n
=
2
L
_
L
0
u
0
(x) sin
_
(2n + 1)
x
2L
_
dx
b
n
=
2
n
L
_
L
0
v
0
(x) sin
_
(2n + 1)
x
2L
_
dx
H. Djelouah
8.2.5 Oscillations forces dun barreau de longueur nie
Oscillations forces dun barreau de longueur nie.
Considrons un barreau dont lextrmit en x = 0 est xe rigidement tandis que lextrmit
situe en x = L est soumise une force sinusodale F (t) = F
0
cos (t).
En notation complexe les conditions aux frontires scrivent :
_
u
x
(0, t) = 0
F
x
(x = L, t) = F
0
e
it
Le milieu de propagation tant de longueur nie, le dplacement de particules u
x
(x, t) scrit
en rgime permanent :
u
x
(x, t) = A e
i(tKx)
+B e
i(t+Kx)
avec K =

V
et
F
x
= ES
u
x
x
= 2iKES
_
A e
i(tKx)
B e
i(t+Kx)
_
En tenant compte des conditions aux limites on obtient les expressions de A et B :
A =
F
0
e
iKL
2iKES cos (KL)
B =
F
0
e
iKL
2iKES cos (KL)
Do lexpression du dplacement de particules :
u(x, t) = U (x) e
it
o lamplitude U (x) sexprime par :
U (x) =
F
0
sin [Kx]
KES cos (KL)
On obtient un phnomne dondes stationnaires dont les amplitudes et les positions des
nuds et des ventres pour le dplacement de particules sont donns par le tableau suivant :
Noeuds Ventres
Position x
n
= L (2n + 1)

4
x
n
= L n
2
Amplitude U
min
= 0 U
max
=
F
0
KES cos(KL)
La rsonance apparat pour des frquences dexcitations gales lune des pulsations
propres du barreau =
n
= (2n + 1)
V
2L
. Pour ces frquences, lamplitude U
max
au niveau des
ventres dlongation devient innie.
H. Djelouah
8.3 Ondes lastiques transversales 75
8.3 Ondes lastiques transversales
Ondes transversales dans un barreau
Nous allons analyser le problme des ondes lastiques transversales dans un barreau solide.
Lorsque lextrmit du barreau est soumise une force de cisaillement, parallle la section S,
nous pouvons supposer que chaque section du barreau se dplace de bas en haut et de haut en bas
sans mouvement horizontal. Appelons u
z
le dplacement transversal dune tranche dpaisseur
x un instant donn. Le dplacement u
z
est fonction de la position x sinon il correspondrait
un dplacement de lensemble du barreau paralllement lui mme. Il en rsulte une dformation
de cisaillement. Chaque tranche dpaisseur x est soumise aux forces antagonistes F (x) et
F (x + x) qui sont tangentes aux sections et qui sont produites par les portions du barreau qui
sont situes de chaque ct du barreau. Il existe entre la force tangentielle de cisaillement et la
dformation de cisaillement, une relation analogue la loi de Hooke :
F
S
= G
u
z
u
x
o G est un coecient caractristique du matriau, que lon nomme module de cisaillement.
La force rsultante sur la tranche x est :
F (x + x) F (x) =
F
x
x
La relation fondamentale de la dynamique pour la tranche x scrit :
F (x + x) F (x) =
F
x
x = S x

2
u
z
t
2
F
x
= S

2
u
z
t
2
La drivation de la loi de Hooke, par rapport x donne :
F
x
= SG

2
u
z
x
2
Par substitution, on obtient
2
u
z
x
2

G
2
u
z
t
2
= 0
A nouveau nous obtenons lquation de propagation dune onde, de cisaillement cette fois,
qui se propage la vitesse
V =
La composante F
z
de la force exerce par la partie gauche du barreau sur llment dpaisseur
x est dnie par :
F
z
= SG
u
z
x
H. Djelouah
On peut montrer que limpdance mcanique du barreau Z scrit :
Z =
F
z
u
z
= SZ
c
o Z
c
= V =
E est limpdance caractristique du matriau constituant le barreau.

8.4 Modle de la chane linaire
Dans ce paragraphe on dveloppera sommairement le modle de la chane linaire datomes
qui permet de dcrire le phnomne de propagation des ondes lastiques dans les solides. Consi-
drons un barreau de section S et de longueur L "trs grande", taill dans un solide cristallin
monoatomique. Si on applique sur la face situe en x = 0 une force de compression F (t), une
onde longitudinale va se propager le long de laxe Ox. tudions le phnomne qui se produit dans
le barreau avant que le front donde nait atteint son extrmit. Nous supposons que le barreau
est un solide monocristallin monoatomique et que les atomes le constituant sont disposs aux
noeuds dun rseau tridimensionnel rgulier. En se propageant une onde plane longitudinale fait
osciller simultanment tous les atomes se trouvant dans un plan perpendiculaire la direction de
propagation Ox. Puisquils se dplacent tous en bloc, ces atomes sont quivalents une masse
unique M concentre sur laxe Ox. Chacun des plans transversaux datomes est maintenu en
place par les forces de liaison qui agissent comme des ressorts placs en parallle ; ils sont donc
quivalents un ressort unique de raideur K. Il sut donc de raisonner sur une seule chane
datomes identiques et quidistants, spars lquilibre par une distance a.
8.4.1 Modlisation microscopique du problme et mise en quations.
O
M K
Modle de la chane linaire
Le solide est constitu dune chane comportant une innit datomes, assimils des points
matriels de mme masse M, relis par des ressorts identiques de longueur vide a et de raideur
K, et susceptibles de se dplacer sans frottement le long de laxe Ox.
Ces ressorts ctifs modlisent, dans lapproximation linaire, les actions subies par les atomes
lorsquils se dplacent au voisinage de leurs position dquilibre. Cest ce couplage entre les
dirents oscillateurs qui permet la propagation dune onde lastique. On repre les positions
lquilibre de latome dordre n par : x
n
[
equ
= n a. Hors quilibre, les abscisses de ces atomes
sont : x
n
= x[
equ
+ u
n
(t) = n a + u
n
(t) ; les dplacements particulaires u
n
(t) supposs faibles
devant a, dpendent la fois du temps et de la position lquilibre na.
Lnergie potentielle de ce systme scrit :
U =
1
2
K (u
1
u
0
)
2
+
1
2
K (u
1
u
0
)
2
+ +
1
2
K (u
n
u
n1
)
2
+
1
2
K (u
n+1
u
n
)
2
+
tandis que lnergie cintique scrit :
T =
1
2
M u
2
0
+
1
2
M u
2
1
+ +
1
2
M u
2
n
+
H. Djelouah
8.4 Modle de la chane linaire 77
Do la fonction de Lagrange :
L = T U =

n
1
2
M u
2
n
n
1
2
K (u
n
u
n1
)
2
Lcriture de lquation de Lagrange permet dobtenir lquation direntielle du mouvement
pour latome dordre n :
M
2
u
n
t
2
= K (u
n
u
n1
) K (u
n
u
n+1
)
M u
n
= K (2u
n
u
n1
u
n+1
)
8.4.2 Solution en rgime permanent sinusodal
Imposons la particule dordre n = 0 une oscillation sinusodale :
u
0
= a
0
e
it
En rgime permanent et en labsence dattnuation, le mouvement de chaque atome est
identique celui de la particule dordre n = 0 un dphasage prs qui correspond au temps de
propagation de londe :
u
n
= a
0
e
i(tkx
n
)
o k est le vecteur donde et x
n
= na. Lquation direntielle du mouvement scrit alors :
_
2K M
2
_
K
_
e
ika
+e
ika
_
= 0
soit
_
2K M
2
_
2K cos (ka) = 0
do
M
2
= 4K sin
2
_
ka
2
_
ou encore
= 2
K
M
sin
_
ka
2
_
Cette dernire relation est appele relation de dispersion. Sa reprsentation graphique est
appele diagramme de dispersion du milieu de propagation (gure cidessous).
/a
/a O
k
C
Diagramme de dispersion
H. Djelouah
Comme

sin
_
ka
2
_
< 1, la frquence des ondes lastiques pouvant se propager dans un cristal

est limite par la frquence de coupure :
f < f
c
=

c
2
=
1
K
M
Lintervalle
a
< k <

a
est appel premire zone de Brillouin. La longueur donde la plus
courte que puisse transmettre le rseau est :
c
=
2
k
c
= 2a
o k
c
=

a
.
Nous remarquons que u
n
peut scrire galement :
u
n
= a
0
e
i
_
t
x
v
_
o v
=

k
reprsente la vitesse de phase.
Pour les faibles valeurs du nombre donde ( ka << 1 ), la relation de dispersion scrit :

K
M
ak
Cest lquation dune droite dont la pente V
0
= a
_
K
M
reprsente la vitesse de propagation
des ondes lastiques de basses frquences. La frquence de coupure peut scrire en fonction de
V
0
:
f
c
=
V
0
a
8.4.3 Lapproximation dun milieu continu.
Dans un rseau cristallin, la distance a entre deux atomes est typiquement de lordre de
10
10
m, distance trs infrieure aux dimensions caractristiques des phnomnes de propagation
tudier (qui sont plutt de lordre de grandeur du mm quelques mtres). Ceci suggre de
considrer la chane datomes comme un milieu continu, dont les dplacements sont dcrits par
une fonction continue u(x, t) prenant les valeurs u
n
(t) aux points dabscisses x
n
= na.
Lquation du mouvement de la particule dordre n peut se rcrire sous la forme :
M u
n
K (u
n+1
u
n
) +K (u
n
u
n+1
) = 0
Si >> a, la dirence u
n+1
u
n
est un inniment petit qui, au premier ordre prs, peut
scrire :
u
n+1
u
n
x
n+1
x
n
=
u
n+1
u
n
a
=
_
u
x
_
x
n+1
u
n
u
n1
x
n
x
n1
=
u
n
u
n1
a
=
_
u
x
_
x
n
Dans ces conditions, lquation direntielle du mouvement devient :
M
2
u
t
2
= Ka
_
_
u
x
_
x
n+1
_
u
x
_
n
_
H. Djelouah
Au premier ordre prs, on peut considrer que :
_
u
x
_
x
n+1
_
u
x
_
x
n
x
n+1
x
n
=

2
u
x
2
et lquation du mouvement scrit alors :
2
u
t
2
=
Ka
2
M
2
u
x
2
Cette quation est quivalente lquation de propagation :
2
u
t
2
= V
0
2
u
x
2
o V
0
= a
_
K
M
est la vitesse de propagation des ondes lastiques de basse frquence.
Ordres de grandeur : La vitesse V
0
des ondes lastiques de basse frquence dans les so-
lides est en gnral comprise entre 1000 m s
1
et 10000 m s
1
. Les distances entre atomes
sont de quelques angstroms. Avec V
0
= 5000 m s
1
et a = 5
A, la frquence de coupure est

f
c
= 3.2 10
12
Hz. Cette valeur est si leve que pour le domaine des frquences infrieures
quelques gigahertz, on se situe au tout dbut de la courbe de dispersion, l o la pulsation
est proportionnelle au nombre donde. La longueur donde =
V
0
f
, comprise dans ces cas entre
quelques mm et quelques m, est trs grande devant les distances interatomiques, si bien que
pour londe le milieu apparat comme continu.
Exercices
Exercice 1 :
x+
u(x,t)
section S
D
Soit un barreau de grande longueur et de faible section S, soumis des vibrations longitudinales.
La masse volumique du barreau et son module dYoung sont respectivement et E. Considrons
un petit lment dpaisseur faible gale x, situ la position x. Lorsque cet lment est
atteint par la vibration, il se met en mouvement sous laction de la rsultante des forces exerces
par les parties du barreau qui se trouvent gauche et droite,. En raison de llasticit du
milieu, les deux sections situes respectivement en x et x + x subissent des dplacements
dirents nots respectivement u(x, t) et u(x +x, t) ; llment subit donc une dformation en
plus du mouvement de translation autour de sa position dquilibre. On ngligera dans la suite
la dformation latrale.
1. Montrer que u(x, t) correspond une onde longitudinale qui se propage une vitesse V
que lon prcisera. Dans le cas dune onde progressive sinusodale, calculer limpdance en
un point quelconque du barreau.
2. Ce barreau, dont la longueur est gale L, est encastr dans une paroi rigide. Son autre
extrmit est libre.
H. Djelouah

0 L
x
F(t)
(a) Oscillations libres : Ecrire lexpression gnrale de u(x, t) sous la forme dondes si-
nusodales de pulsation . Ecrire les conditions aux limites en x = 0 et x = L. En
dduire les pulsations propres du barreau.
(b) Oscillations forces : Lextrmit du barreau en x = 0 est soumise une force hori-
zontale F(t) = F
0
cos(t) . Montrer que le dplacement en chaque point scrit sous
la forme u(x, t) = U(x)cos(t +) ; quelle est lexpression de lamplitude U(x) et de
la phase . Quelle est la position des minima et des maxima de vibration? Quelles
sont les amplitudes U
min
et U
max
en ces points. Pour quelles pulsations obtient-on le
phnomne de rsonance ?
Exercice 2 : Un barreau de longueur L est x rigidement en x = 0 ; son extrmit en x = L
est libre.
1. Montrer que seuls les harmoniques impairs sont permis.
2. Dterminer la frquence fondamentale du barreau sil est constitu dacier et que sa lon-
gueur est L = 0.5 m.
3. Si une force statique est applique lextrmit libre du barreau de telle sorte dplacer
cette extrmit dune longueur gale h, montrer que, lorsque le barreau vibre suite une
suppression brusque de cette force, les amplitudes des dirents harmoniques de vibration
sont donns par A
n
=
_
8h/n
2
sin (n/2) .
4. Dterminer ces amplitudes si la force statique vaut F
S
= 5000 N et si la section droite du
barreau a une surface gale s = 0.00005 m
2
.
N.B : Rechercher pralablement les caractristiques mcaniques de lacier dans la bibliographie.
Exercice 3 : Un barreau dacier de 0.0001 m
2
de section droite et de 0.25 m de longueur est
libre de se mouvoir en x = 0 et il est charg lautre extrmit , en x = 0.25 m, par une masse
de 0.15 kg.
1. Calculer la frquence fondamentale des vibrations longitudinales de ce barreau.
2. Dterminer la position laquelle ce barreau doit tre x pour causer la plus faible per-
turbation de son mode fondamental de vibration.
3. Quand ce barreau vibre dans son mode fondamental, quel est le rapport de lamplitude du
dplacement de lextrmit libre celle qui est charge par la masse ?
4. Quelle est la frquence du premier harmonique de ce barreau?
Exercice 4 : Une masse m = 2 kg est suspendue un l dacier de longueur = 1.0 m et de
section droite s = 0.00001 m
2
.
1. Calculer la frquence fondamentale des oscillations verticales de la masse en la considrant
comme un simple oscillateur.
2. Calculer la frquence fondamentale des oscillations verticales du systme constitu par un
barreau vibrant x une extrmit et charg par une masse lautre extrmit.
3. Montrer que pour kL < 0.2, lquation obtenue la question prcdente peut se mettre
sous la forme :
0
=
_
s/m.
H. Djelouah
Exercice 5 : Soit une chane linaire de particule identiques de masse m. A lquilibre, la masse
dordre n est situe, sur laxe Ox, au point dabscisse x
n
= n a, x
n
tant ngatif ou nul (Figure
a). Les masses sont relies entre elles par des ressorts identiques de raideur K, dont la longueur
au repos est a. Soit u
n
lcart de la particule dordre n par rapport la position dquilibre.

0 x
x'
-a -2a -3a
m m m m m
u
n
-na
0
x
x'
-a -2a -3a
m
m m m m
u
n
-na
K'
Figure (a)
Figure (b)
a
1. Ecrire lquation du mouvement de la particule dordre n.
2. En cherchant les solutions sous la forme dondes progressives sinusodales planes telles que
u
n
= U
0
e
i(tkna)
, o U
0
est une constante relle, dterminer la relation de dispersion
= (k).
3. La particule en x
0
= 0 est xe. On envoie une onde incidente de la gauche vers la droite
dcrite par u
n
= U
0
e
i(tkna)
. Dterminer lamplitude U
et la phase de londe rchie.

4. La particule en x = 0 est maintenant lie un bti xe par lintermdiaire dun ressort
de raideur K
et dun amortisseur de coecient de frottement visqueux (Figure b). On

choisit K
et pour quil ny ait pas donde rchie.

(a) Ecrire lquation du mouvement de la masse situe en x = 0.
(b) On envoie une onde incidente comme prcdemment. Dterminer les coecients K
et pour que cette masse vibre sous leet de la seule onde incidente (pas donde
rchie).
Exercice 6 : Soit une corde plombe telle que reprsente sur la gure ci-dessous, o x
n
reprsente la position de la masse m et u
n
son dplacement. Les plombs sont espacs lun de
lautre de a et relis entre eux par des segments de l de tension T
0
que lon supposera constante
lors des dplacements des masses. Cette corde plombe de longueur L telle que L >> a, subit
une vibration transversale.

0 a
x
u
n
x
n
m
m
m
m
m
m
Dans le cas des vibrations de faible amplitude, on demande de :
1. Ecrire lquation du mouvement du plomb dordre n.
2. Chercher les solutions de cette quation sous la forme dune onde progressive.
3. En dduire la relation entre la pulsation et le vecteur donde k.
4. Montrer que lon peut limiter ltude lintervalle 0 < [k[ < /a. Tracer la courbe =
(k).
H. Djelouah
5. Calculer la pulsation de coupure
M
.
6. Dnir la vitesse de phase V
et la vitesse de groupe V
G
. Dcrire le mouvement lorsque
k = /a.
7. Dans le cas des trs grandes longueurs donde, que deviennent V
et V
G
?
H. Djelouah
Chapitre 9
Ondes acoustiques dans les uides
9.1 Introduction
Les ondes acoustiques sont des ondes lastiques qui se propagent dans les uides (gaz ou
liquides). Il est donc possible dobtenir lquation donde qui rgit la propagation des ondes
planes dans un uide par la mme dmarche que celle que nous avons utilise pour tablir
lquation de propagation des ondes transversales dans une corde.
Dans la suite, nous utiliserons les symboles suivants pour tudier londe acoustique qui se
propage suivant laxe des x :
x : coordonne lquilibre dune particule du milieu.
u
x
: composante suivant laxe des x du dplacement de particule par rapport la position
dquilibre.
0
: masse volumique du uide lquilibre
P : pression instantane en un point quelconque
P
0
: pression lquilibre
p = P P
0
: surpression ou pression acoustique
c : vitesse de propagation de londe
On entend par particule, un lment de volume contenant des millions de molcules de telle
sorte quil puisse tre considr comme continu, mais toutefois susamment petit pour que les
grandeurs acoustiques comme la pression, la masse volumique et la vitesse de particule puissent
tre considres comme constantes dans cet lment de volume. Dans ce qui suit, nous ngligerons
les eets de la gravitation de telle sorte que P
0
et
0
sont uniformes dans tout le milieu. On
suppose dautre part que le milieu est homogne, isotrope et parfaitement lastique, cest--dire
non dissipatif.
9.2 Equation donde
Considrons le cas dune onde plane mise dans un uide par une membrane vibrante plane.
Lorsque celle-ci est au repos, la pression dans le uide est uniforme et gale P
0
. En se dplaant,
par exemple dans le sens des x positifs, la membrane comprime la couche de uide adjacente.
Cette situation est instable : le uide se dtend en comprimant son tour la tranche voisine.
Londe progresse ainsi de proche en proche par une succession de compressions et de dtentes.
H. Djelouah
84 Ondes acoustiques dans les uides
x
x+dx
u
x
(x)
u
x
(x+dx)
P(x) P(x+dx)
S
dx
Propagation dune onde acoustique
Soit une tranche de uide de petite paisseur x situe labscisse x. Lorsque la perturbation
atteint ce point, les forces agissant sur cette tranche ne squilibrent plus et elle se met en
mouvement. Soit u
x
(x, t) le dplacement linstant t du plan dabscisse x. Soit F
x
(x, t) et
F
x
(x + x, t) les forces agissant sur la tranche de uide respectivement en x et x + x. Ces
forces sexpriment par :
F
x
(x, t) = S P (x, t)
F
x
(x + x, t) = S P (x + x, t)
La rsultante de ces deux forces est :
F
x
= F
x
(x, t) +F
x
(x + x, t)
F
x
= S [P (x + x, t) P (x, t)]
En faisant un dveloppement en srie de Taylor au premier ordre de P (x, t), on obtient :
P(x + x, t) = P (x, t) +
P
x
x
Do :
F
x
= S
P
x
x
Comme P = P
0
+p, la force rsultante sexprime par :
F
x
= S
p
x
x
Sous laction de cette force, la tranche de uide subit une acclration et en crivant la
relation fondamentale de la dynamique, on obtient :
m

2
u
x
t
2
= S
p
x
x
Le uide tant compressible, le dplacement du plan dabscisse x + x est dirent du
dplacement du plan dabscisse x et il vaut u
x
(x + x, t). De nouveau un dveloppement en
srie de Taylor au premier ordre permet dcrire :
u
x
(x + x, t) = u
x
(x, t) +
u
x
x
x
Pour prendre en compte la compressibilit du uide, calculons la dilatation volumique subie
par la tranche de uide . Soit v
0
= S x, le volume lquilibre et soit v, le volume en cours
de mouvement, avec :
H. Djelouah
9.3 Vitesse du son 85
v = S [x + x +u
x
(x + x) x u
x
(x)]
v = S [x +u
x
(x + x) u
x
(x)]
v = S
_
x +
u
x
x
x
_
v = v
0
+
u
x
x
v
0
On en dduit la dilatation volumique
=
v v
0
v
0
=
u
x
x
Rappelons que pour un uide compressible, la surpression p est relie la dilatation volu-
mique par la relation
p =
o est le module de compressibilit. On obtient ainsi :
p =
u
x
x
Remarque : On utilise souvent le coecient de compressibilit =
1
.
Les deux quations
2
u
x
t
2
=
p
x
p =
u
x
x
constituent les deux quations fondamentales de lacoustique.
En remplaant dans la premire quation p par son expression tire de la seconde quation
on obtient lquation de propagation :
2
p
x
2

1
V
2
2
p
t
2
= 0
o V reprsente la vitesse de propagation dnie par
V =
_

0
=
1
9.3 Vitesse du son

Le phnomne de propagation tant un processus adiabatique, la relation liant la pression
et le volume est
Pv
= constante
En calculant la direntielle, on obtient :
v
dP +P v
1
dv = 0
H. Djelouah
Si lon considre que dP reprsente la variation de pression au voisinage de la pression
lquilibre P
0
, on obtient :
v
0
p +P
0
v
1
0
v = 0
do :
p = P
0
v
v
0
En tenant compte de la dnition du module de compressibilit, on obtient :
=
1
= P
0
Do la vitesse du son dans un uide :
V =
P
0
0
Exemple : Dans lair, dans les conditions normales T = 20
C et P
0
= 10
5
N m
2
, = 1.4
et
0
= 1.29 kg m
3
, on en dduit V 330 m s
1
La valeur de la pression lquilibre dpend fortement de la temprature. Pour une mole de
gaz parfait, on a :
P
0
v
0
= RT
do
P
0
=
RT
v
0
et
V =
RT
0
v
0
Le produit
0
v
0
reprsente la masse molaire M du gaz ; do :
V =
RT
M
Dans un gaz parfait, la vitesse de propagation du son est proportionnelle la racine carre
de la temprature mesure en kelvin (K).
9.4 Onde progressive sinusodale
9.4.1 Dnition
Une onde acoustique sinusodale, scrit :
p (x, t) = p
0
cos
_
_
t
x
V
__
On dnit le module du vecteur donde k par
k =

V
do
p (x, t) = p
0
cos (t kx)
H. Djelouah
9.4 Onde progressive sinusodale 87
En notation complexe, londe progressive sinusodale scrit
p (x, t) = p
0
e
i(tkx)
La relation liant la pression acoustique et la compressibilit, savoir
p =
u
x
permet dcrire
u(x, t) =
1
_
p (x, t) dx
u(x, t) =
1
_
p
0
e
i(tkx)
dx
u(x, t) =
p
0
ik
e
i(tkx)
u(x, t) =
p
0
i
0
V
e
i(tkx)
La drivation de cette dernire expression par rapport au temps permet dobtenir la vitesse
de particules :
u(x, t) =
u
t
=
1
0
V
p
0
e
i(tkx)
On constate que pour une onde progressive la vitesse de particules est en phase avec la
pression acoustique.
9.4.2 Impdance acoustique
On appelle impdance acoustique en un point le rapport de lamplitude complexe de la
pression lampliude complexe de la vitesse de particule
Z (x) =
p
u
Dans le cas dune onde progressive, on obtient :
Z (x) =
0
V
Le produit
0
V dnit limpdance acoustique caractristique du uide
Z
c
=
0
V
On obtient une proprit de londe plane progressive :
Z (x) = Z
c
x
9.4.3 Energie acoustique
Densit dnergie cintique
Soit un petit lment de volume v
0
dont le dplacement est u(x, t) et dont la vitesse est
u(x, t) ; il possde une nergie cintique
E
c
=
1
2
0
v
0
u
2
On dnit lnergie cintique par unit de volume ou densit dnergie cintique
c
c
=
E
c
v
0
=
1
2
0
u
2
H. Djelouah
Densit dnergie potentielle
Soit un petit lment de volume v
0
. Sous laction de la surpression p, cet lment se comprime
ou se dilate en raison de la compressibilit du uide. Lnergie potentielle emmagasine est gale
au travail fourni par la pression pour comprimer ou dilater le volume v
0
:
E
p
=
_
pdv
Sachant que
p =
v v
0
v
0
on en dduit que :
dv =
1
v
0
dp
do :
E
p
=
v
0
_
p
0
p dp
Ep =
v
0
2
p
2
On en dduit la densit dnergie potentielle :
c
p
=
E
p
v
0
=
1
2
p
2
Densit dnergie
La densit dnergie est gale la somme de la densit dnergie cintique et de la densit
dnergie potentielle
c = c
c
+c
p
c =
1
2
0
u
2
+
1
2
p
2
Dans le cas particulier dune onde plane progressive sinusodale,
c
c
= c
p
=
1
2
0
V
2
p
0
cos
2
(t kx)
et
c =
1
0
V
2
p
0
cos
2
(t kx)
On dnit la valeur moyenne temporelle de la densit dnergie comme
c) =
1
T
_
t+T
t
c dt
o T =
2
.
H. Djelouah
9.4 Onde progressive sinusodale 89
On dnit galement la moyenne spatiale de la densit dnergie :
c) =
1
_
x+
x
c dx
Dans le cas dune onde progressive, ces deux valeurs sont gales et valent :
c) =
p
2
0
2
0
V
2
Intensit
On appelle intensit de londe acoustique la puissance qui traverse, par unit de temps, une
surface unit perpendiculaire la direction de propagation.
Pour calculer lintensit de londe calculons lnergie qui traverse pendant un intervalle de
temps une surface S perpendiculaire la direction de propagation.
V dt
t t+dt
S
V
Flux de puissance
Cette nergie dE est gale lnergie contenue dans un volume S V dt et elle est gale
dE = c S V dt
Do la puissance T traversant cette surface
T =
dE
dt
= c S V
On en dduit lexpression de lintensit de londe acoustique
I (t) =
1
S
P
I (t) = c V
I (t) =
p
2
0
0
V
cos
2
(t kx)
On appelle intensit de londe acoustique la valeur moyenne
I =
1
T
_
t+T
t
I (t) dt
I =
p
2
0
2
0
V
I =
p
2
0
2Z
c
H. Djelouah
Niveau sonore
On dnit le niveau sonore en dcibels par
N
dB
= 10 log
_
I
I
0
_
I
0
est une intensit de rfrence correspondant I
0
= 10
12
W m
2
.
Exemple : Pour une frquence f = 1kHz, le seuil daudition est gal 0 dB et le seuil de
douleur est gal 130 dB. Pour calculer lintensit, lamplitude de pression p
0
la vitesse de
particules et le dplacement de particules, dans le cas o V = 330 m/s et Z
c
= 411 rayleighs,
on peut utiliser les relations suivantes :
I = I
0
10
0.1 N
dB
p
0
=
2Z
c
I
u =
p
0
Z
c
u =
u
2f
Pour chacun de ces deux cas, on obtient :
N
dB
I
_
W/m
2
_
p
0
( Pa ) u( m/s ) u( m )
0 dB 10
12
2. 9 10
5
7 10
8
1. 1 10
11
130 dB 10.0 91 0. 22 3. 5 10
5
9.5 Rexion-Transmission
2
, V
2
1
, V
1
x x O
Onde incidente
Onde rflechie
Onde transmise
Rexion un interface uide-uide
Soit deux milieux uides semi-innis spars par un surface plane. Choisissons un repre
orthonorm de telle sorte que le plan yOz concide avec la surface de sparation. Lorsque une
onde acoustique provenant de , se propageant dans le premier dans la direction de laxe des
x arrive la surface de sparation, elle donne naissance deux ondes
une onde rchie qui se propage dans le premier milieu dans le sens des x dcroissants.
une onde transmise qui se propage dans le second milieu dans le sens des x croissants.
Londe rsultante dans le premier milieu (x 0) est caractrise par :
p
1
(x, t) = p
i
(x, t) +p
R
(x, t)
p
1
(x, t) = P
i
e
i(tk
1
x)
+P
R
e
i(t+k
1
x)
u
1
(x, t) =
1
Z
1
_
P
i
e
i(tk
1
x)
P
R
e
i(t+k
1
x)
_
Dans le deuxime milieu, on a
H. Djelouah
9.5 Rexion-Transmission 91
p
2
(x, t) = p
T
(x, t)
p
2
(x, t) = P
T
e
i(tk
2
x)
u
2
(x, t) =
1
Z
2
P
T
e
i(tk
2
x)
Les relations de continuit linterface scrivent
_
p
1
(0, t) = p
2
(0, t)
u
1
(0, t) = u
2
(0, t)
On en dduit
_
_
_
P
i
+P
R
= P
T
1
Z
1
(P
i
P
R
) =
1
Z
2
P
T
ou encore
_
_
1 +
P
R
P
i
=
P
T
P
i
1
P
R
P
i
=
Z
1
Z
2
P
T
P
I
On dnit
le coecient de rexion pour la pression
R
P
=
P
R
P
i
le coecient de transmission pour la pression
T
P
=
P
T
P
i
Les deux relations de continuit scrivent alors
_
1 +R
P
= T
P
1 R
P
=
Z
1
Z
2
T
P
On en dduit les coecients de rexion et de transmission
R
P
=
Z
2
Z
1
Z
2
+Z
1
T
P
=
2Z
2
Z
2
+Z
1
En tenant compte des relations p
i
= Z
1
u
i
, p
R
= Z
1
u
R
et p
T
= Z
2
u
T
, on peut calculer les
coecients de rexion et de transmission pour la vitesse de particules et pour le dplacement
de particules :
R
U
= R
U
=
Z
1
Z
2
Z
1
+Z
2
T
U
= T
U
=
2Z
1
Z
1
+Z
2
H. Djelouah
En tenant compte des relations I
i
= P
2
i
/2Z
1
, I
R
= P
2
R
/2Z
1
et I
T
= P
2
T
/2Z
2
, on peut calculer
les coecients de rexion et de transmission pour lintensit acoustique :
R
=
I
R
I
i
=
_
Z
1
Z
2
Z
1
+Z
2
_
2
T
=
I
T
I
i
=
4Z
1
Z
2
[Z
1
+Z
2
]
2
9.6 Eet Doppler
9.6.1 Dnition
On appelle eet Doppler le changement apparent de la frquence dun signal lectromagn-
tique (radio ou lumineux)ou acoustique reu par un observateur mobile par rapport une source
mettrice xe ou bien par un observateur xe par rapport une source mettrice mobile. La
variation apparente de frquence est proportionnelle la vitesse relative entre lobservateur et
la source le long du chemin qui les spare. Si la source dondes oscillant avec la frquence
0
se
dplace par rapport au milieu avec la vitesse v
1
et lobservateur avec la vitesse v
2
, la frquence
, perue par lobservateur sera alors :
=
0
1 +
v
2
V
cos
2
1 +
v
1
V
cos
1
o V est la vitesse des ondes dans le milieu immobile,
1
et
2
sont les angles forms par les
vecteurs v
1
et v
2
avec le vecteur

R reliant le rcepteur la source dondes.
9.6.2 Cas particulier des faibles vitesses
Dans le cas o v
1
/V << 1 et v
2
/V << 1, on peut appliquer la formule approche
=
0
_
1
v
V
cos
_
o v est la vitesse relative de la source et du rcepteur (v = v
1
v
2
), tant langle entre v et
R.
Si la source et lobservateur se rapprochent, langle est obtus, cos < 0 et >
0
; si la
source et lobservateur sloignent lun de lautre, langle est aigu, cos > 0 et <
0
Exercices
Exercice 1 : Dans les conditions normales de temprature et de pression, lair est caractris
par une masse volumique lquilibre = 1.21 kg/m
3
et une valeur de = c
p
/c
v
= 1.402.
Calculer la vitesse de propagation du son dans lair et son impdance acoustique spcique dans
ces conditions de temprature et de pression (T = 20C et P
0
= 10
5
N/m
2
).
Exercice 2 : Soit une onde acoustique plane de frquence f = 24 kHz, qui se propage dans
leau avec une vitesse c = 1480 m/s. Elle vhicule une puissance moyenne de T = 1W unifor-
mment rpartie sur une section circulaire de de diamtre D = 40 cm, normale la direction de
propagation. La frquence de londe est f = 24 kHz.
1. Calculer lintensit acoustique ; quel est en dB le niveau de lintensit acoustique relative-
ment un niveau de rfrence I
0
= 10
12
W/m
2
?
H. Djelouah
9.6 Eet Doppler 93
2. Calculer lamplitude de la pression acoustique, lamplitude de la vitesse de particules et
lamplitude du dplacement de particules.
3. Comparer aux rsultats que lon aurait obtenus si cette onde se propageait dans lair.
Exercice 3 : Une onde acoustique plane se propageant dans leau arrive en incidence normale
la surface de sparation avec lair. Calculer les valeurs numriques des rapports suivants :
P
R
/P
i
, P
T
/P
i
, U
R
/U
i
, U
T
/U
i
,

U
R
/

U
i
,

U
T
/

U
i
, I
R
/I
i
, I
T
/I
i
o U,

U, P et I reprsentent respecti-
vement le dplacement des particules, la vitesse des particules, la pression acoustique et lin-
tensit acoustique. Les indices i, R et T se rapportent respectivement londe incidente, londe
rchie et londe transmise.
Exercice 4 : Rpondre aux mmes questions que pour lexercice prcdent en supposant que
londe acoustique se propage initialement dans lair et se transmet dans leau. Comparer aux
rsultats de lexercice prcdent.
Exercice 5 : Un tuyau cylindrique de section S constante est rempli dun gaz, de masse volu-
mique , o les ondes acoustiques peuvent se propager la vitesse V . A lune des extrmits
du tuyau, en x = 0, on place un piston plan qui est anim, suivant laxe Ox du tuyau, dun
dplacement sinusodal damplitude U
0
et de pulsation . A la position x = L, le tuyau est
ferm par une paroi rigide.
1. Montrer que le dplacement peut se mettre sous la forme : u(x, t) = U(x) e
i(t+)
o U(x)
est rel. Donner lexpression de lamplitude U(x) et de la phase de londe rsultante.
2. En dduire les positions et les valeurs des maxima et des minima de lamplitude U(x) en
valeur absolue.
3. Pour quelles frquences obtient-on un phnomne de rsonance ? Quelle est alors lampli-
tude du dplacement au niveau des ventres de dplacement.
4. Dans le cas o L = 13/12, tant la longueur donde, tracer sur un graphe les variations
de [U(x)[ en fonction de x. Echelle : 1 cm = /12. Quel est le nombre de maxima (ventres)
et de minima (noeuds) ?
Exercice 6 : Une onde acoustique plane, sinusodale de pulsation , damplitude A
1
, se propage
suivant la direction Ox dans un milieu uide de masse volumique
1
. Elle arrive sous incidence
normale sur un second milieu uide de masse volumique
2
et dpaisseur L
2
, dpos sur un solide
parfaitement rigide (voir gure).On notera V
1
et V
2
les vitesses de propagation respectives dans
chacun des deux milieux uides. Les vecteurs donde correspondants seront nots respectivement
k
1
et k
2
.

Onde
Incidente
L
2
x'
O
x
Milieu 1
Milieu 2
Solide rigide
H. Djelouah
Dans chacun des deux milieux, la pression acoustique scrit respectivement
p
1
(x, t) = A
1
e
i(tk
1
x)
+A
1
e
i(t+k
1
x)
p
2
(x, t) = A
2
e
i(tk
2
x)
+A
2
e
i(t+k
2
x)
1. Ecrire les expressions respectives, u
1
(x, t) et u
2
(x, t) , des vitesses de particule dans le
milieu 1 et dans le milieu 2.
2. Ecrire les relations de continuit pour la pression acoustique et pour la vitesse de particule
en x = 0. En dduire deux relations entre les coecients A
1
, A
1
, A
2
et A
2
.
3. Ecrire la relation de continuit pour la vitesse de particule en x = L
2
. En dduire une
relation entre les coecients A
2
et A
2
4. En dduire le coecient de rexion R =
A
1
A
1
. En donner le module et la phase.
5. Mesure de la vitesse V
2
(a) Quelle est la condition pour que, dans le milieu 2, la pression possde un nud en
x = 0 et un seul ventre ?
(b) Sachant que le premier nud de pression dans le milieu 1 se situe en x = L
1
, calculer
la vitesse de propagation V
2
en fonction de V
1
, L
1
et L
2
.
(c) Lexprience est ralise, dans les conditions ci-dessus, avec de leau comme milieu 1
(V
1
= 1500 m/s) et de la glycrine comme milieu 2. On mesure L
1
= 7.5 mm et L
2
=
4.95 mm. Quelle est la vitesse de propagation V
2
des ondes acoustiques dans la gly-
crine ?
Exercice 7 :
Source Rcepteur Source Rcepteur
Figure 1 Figure 2
Un rcepteur capte les ondes sonores mises par une source dans un milieu o le son se propage
la vitesse V . N ondes sont mises pendant le temps t.
1. Le rcepteur tant au repos et la source se dplaant la vitesse v (gure 1), quelle est la
distance qui spare deux ondes successives ? En dduire la frquence
R
ans le systme de
rfrence (R) li au rcepteur et la comparer la frquence
S
de londe dans le systme
de rfrence (S) li la source.
2. La source sonore est maintenant immobile et le rcepteur se dplace une vitesse v
(gure 2). Quelle est la frquence
0
de la frquence
R
de la vibration sonore reue par le
rcepteur ?
3. Comparer les rsultats de 1) et 2) dans le cas o V >> v. Conclusion.
H. Djelouah
Annexe A
Equations direntielles
A.1 Introduction
Les oscillations linaires des systmes un degr de libert sont rgies par des quations
direntielles du second ordre coecients constants. Une quation direntielle linaire du
second ordre coecients constants est une relation entre une variable dpendante y et ses
drives premire et seconde par rapport une variable indpendante t, qui peut scrire sous
la forme :
d
2
y
dt
2
+ 2
dy
dt
+
2
0
y = A(t)
Les coecients et
0
sont des constantes relles positives. Dans les problmes de vibration
le paramtre t reprsente le temps et on note par convention :
dy
dt
= y
d
2
y
dt
2
= y
Do lcriture de lquation direntielle :
y + 2 y +
2
0
y = A(t)
A.2 Equation homogne
Lquation direntielle est dite homogne si A(t) = 0 :
y + 2 y +
2
0
y = 0
On recherche des solutions qui sont de la forme y(t) = e
st
. Dans ce cas lquation direntielle
scrit :
_
s
2
+ 2 s +
2
0
_
e
st
= 0
Cette quation doit tre vraie quel que soit t, ce qui implique :
s
2
+ 2 s +
2
0
= 0
On obtient ainsi une quation du second degr en s dite quation caractristique. Les racines
de cette quation caractristique sont :
H. Djelouah
96 Equations direntielles
s
1
= +
_
2
0
s
2
=
_
2
0
La solution de lquation direntielle scrit alors :
y(t) = A
1
e
s
1
t
+A
2
e
s
2
t
A
1
et A
2
sont deux constantes dintgration que lon peut dterminer partir des conditions
initiales :
y(t = 0) = y
0
y(t = 0) = y
0
Sachant que et
0
sont des nombres rels positifs, s
1
et s
2
sont ngatives ou complexes avec
une partie relle ngative. La nature des solutions s
1
et s
2
de lquation caractristique dpend
de la valeur relative de par rapport
0
. Ainsi trois cas sont envisager :
A.2.1 Rgime fortement amorti ( >
0
)
Dans ce cas, les deux racines s
1
et s
2
sont relles et ngatives. Lcriture des conditions
initiales donne un systme de deux quations :
A
1
+A
2
= y
0
s
1
A
1
+s
2
A
2
= y
0
dont les solutions sont les constantes dintgration A
1
et A
2
:
A
1
=
s
2
y
0
y
0
s
2
s
1
A
2
=
y
0
s
1
y
0
s
2
s
1
y(t) est une fonction dcroissant sans oscillations vers zro lorsque t augmente. La forme
exacte de y(t) dpend des valeurs de A
1
et A
2
qui sont dtermines par les conditions initiales.
Pour les conditions initiales particulires suivantes :y
0
,= 0; y
0
= 0, la gure suivante reprsente
les variations de y au cours du temps
O
Rgime apriodique
H. Djelouah
A.2 Equation homogne 97
A.2.2 Rgime critique ( =
O
)
Lquation caractristique possde une racine double :
s
1
= s
2
=
y(t) = (A
1
+A
2
t) e
t
Les constantes dintgration A
1
et A
2
sont dtermines partir des conditions initiales et
valent :
A
1
= y
0
A
2
= y
0
+ y
0
y(t) et une fonction dcroissant vers zro quand t augmente. Il est ais de vrier que cette
situation correspond la dcroissance la plus rapide de y(t). Ce cas correspond au rgime
critique. Pour le cas particulier de conditions initiales :y
0
,= 0; y
0
= 0, la solution est :
y (t) = y
0
e
t
(1 +t)
La gure ci-dessous reprsente les variations de y(t).
O
Rgime critique
A.2.3 Rgime pseudo-priodique ( <
0
)
Dans ce cas s
1
et s
2
sont complexes conjugus :
s
1
= +i
_
2
0

2
s
2
= i
_
2
0

2
o i reprsente le nombre imaginaire pur vriant la relation i
2
= 1. Posons :
D
=
_
2
0

2
La solution gnrale scrit alors :
H. Djelouah
y(t) = e
t
_
A
1
e
i
D
t
+A
2
e
i
D
t
_
Sachant que :
e
i
D
t
= cos(
D
t) +i sin(
D
t)
e
i
D
t
= cos(
D
t) i sin(
D
t)
y(t) scrit :
y(t) = e
t
[(A
1
+A
2
) cos(
D
t) +i (A
1
A
2
) sin(
D
t)]
y(t) tant relle, les nombres complexes A
1
et A
2
doivent vrier les relations :
A
1
+A
2
: rel
A
1
A
2
: imaginaire
A
1
et A
2
sont donc complexes conjugus et peuvent se mettre sous la forme :
A
1
= A
e
i
A
2
= A
e
i
y(t) scrit alors :
y(t) = A
e
t
_
e
i(
D
t+)
+e
i(
D
t+)
_
soit nalement, en posant A = 2A
:
y(t) = A e
t
cos(
D
t +)
y(t) peut tre interprte comme une fonction priodique de pulsation
D
, de phase initiale
et damplitude Ae
t
dcroissant exponentiellement au cours du temps. On peut dnir une
pseudo-priode
T
D
=
2
D
A et sont deux constantes dintgration dnies partir des conditions initiales :
y
0
= A cos()
y
0
= A cos() [ +
D
tan()]
Do lon tire :
H. Djelouah
A.2 Equation homogne 99
= arctan
_
y
0
+y
0
D
y
0
_
A =
_
(
D
y
0
)
2
+ ( y
0
+y
0
)
2
D
La gure ci-dessous reprsente les variations de y(t) dans le cas particulier de conditions
initiales :y
0
,= 0; y
0
= 0.
O
Rgime pseudo-priodique
Remarque : Cas particulier o = 0 :
Lquation direntielle scrit :
y +
2
0
y = 0
La solution sexprime dans ce cas :
y(t) = A cos(
0
t +)
Cette solution est appele solution harmonique car y(t) est une fonction sinusodale du
temps, de pulsation
0
, de priode T
0
= 2/
0
et dont lamplitude A et la phase initiale sont
dtermines par les conditions initiales :
y
0
= A cos()
y
0
=
0
A sin()
do lon tire :
= arctan
_
0
y
0
y
0
_
A =
y
2
0
+
_
y
0
0
_
2
La gure suivante reprsente les variations au cours du temps de y(t) dans le cas particulier
o : y
0
= 1 et y
0
= 0.
H. Djelouah
Oscillations non amorties
A.3 Equation avec second membre
A.3.1 Solution gnrale
Soit y(t) la solution gnrale de lquation direntielle avec second membre :
y + 2 y +
2
0
y = A(t)
Soit y
H
(t) la solution de lquation homogne et soit y
P
(t) une solution particulire de
lquation avec second membre ; y
H
(t) et y
P
(t) sont les solutions respectives des deux quations
direntielles suivantes :
y
H
+ 2 y
H
+
2
0
y
H
= 0
y
P
+ 2 y
P
+
2
0
y
P
= A(t)
Les oprations de drivation qui interviennent tant des oprations linaires, laddition
membre membre des deux quations direntielles prcdentes donne :
( y
H
+ y
P
) + 2 ( y
H
+ y
P
) +
2
0
(y
H
+y
P
) = A(t)
Ainsi la solution gnrale peut tre obtenue en faisant la somme de la solution homogne et
dune solution particulire :
y(t) = y
H
(t) +y
P
(t)
A.3.2 Cas particulier o A(t) est constante
Considrons le cas particulier important o A(t) = A
0
, A
0
tant une constante relle.
y + 2 y +
2
0
y = A
0
On peut vrier que
y =
A
0
2
0
constitue une solution particulire de lquation avec second membre. Selon le cas la solution
gnrale de lquation avec second membre sera :
Rgime fortement amorti ( >
0
)
H. Djelouah
A.3 Equation avec second membre 101
y(t) = A
1
e
s
1
t
+A
2
e
s
2
t
+
A
0
2
0
Rgime critique ( =
0
)
y(t) = (A
1
+A
2
t) e
t
+
A
0
2
0
Rgime pseudo-priodique ( <
0
)
y(t) = A e
t
cos(
D
t +) +
A
0
2
0
Dans les trois cas considrs les constantes dintgration A
1
, A
2
, A et sont dtermines
partir des conditions initiales. Considrons titre dexemple le cas particulier y
0
= 0 et y
0
= 0 .
La rsolution des systmes dquations obtenus permet de calculer les constantes dintgration
et de tracer les variations de y(t) pour les trois rgimes. Les variations correspondantes de y(t)
sont reprsentes par la gure ci-dessous.
O
Cas o A(t) est une constante.
A.3.3 Cas particulier o A(t) = A
0
cos(t) :
Nous pouvons vrier que y
P
(t) = Y
0
cos(t + ) constitue une solution particulire de
lquation direntielle avec second membre condition que lamplitude Y
0
et la phase vrient
la relation :
_
2
0

2
_
Y
0
cos(t +) 2 Y
0
sin(t +) = A
0
cos(t)
Le dveloppement des termes en cosinus et en sinus permet dobtenir :
Y
0
=
A
0
_
[
2
0

2
]
2
+ 4
2
2
= arctan
_
2
2
0

2
_
La solution complte scrit alors suivant le cas :
Rgime fortement amorti ( >
0
)
y(t) = A
1
e
s
1
t
+A
2
e
s
2
t
+Y
0
cos(t +)
Rgime critique ( =
0
)
H. Djelouah
y(t) = (A
1
+A
2
t) e
t
+Y
0
cos(t +)
Rgime pseudo-priodique ( <
0
)
y(t) = A e
t
cos(
D
t +) +Y
0
cos(t +)
Comme dans le cas prcdent les constantes dintgration A
1
, A
2
, A et sont dtermines
partir des conditions initiales. La gure suivante reprsente le rsultat obtenu dans le cas
particulier o :( y
0
= 0 , y
0
= 0 ).
Cas o A(t) est une fonction sinusodale
On remarque que dans tous les cas la solution homogne tend zro lorsque t augmente, et la
solution gnrale sidentie alors avec la solution particulire :
y(t) y
P
(t)
Pour cette raison la solution de lquation homogne est appele solution transitoire tandis
que la solution particulire est appele solution permanente.
A.3.4 Cas o A(t) est une fonction priodique du temps
Introduction
Nous avons tudi dans le paragraphe prcdent la solution de lquation direntielle dans le
cas harmonique, cest--dire lorsque le second membre est une fonction sinusodale de la variable
t. En considrant le cas de fonctions priodiques, nous procderons une gnralisation du cas
harmonique.
Dveloppement en srie de Fourier dune fonction priodique
Les fonctions priodiques Une fonction f(t) est dite priodique, de priode T, si pour tout
t, f(t + T) = f(t) o T est une constante positive. La plus petite valeur non nulle de T est
appel la priode de f(t).
Exemples :
1. La fonction sin(t) reprend les mmes valeurs pour t = 2, 4, 6 puisque sin[(t + 2)] =
sin[(t + 4)] = sin[(t + 6)] = sin(t). Cependant 2 est la priode de sin(t).
2. La priode de sin(t) ou de cos(t) est 2/. La priode de sin(nt) et de cos(nt) est
2/n.
3. Une constante a pour priode nimporte quel nombre positif.
H. Djelouah
4. Les gures ci-dessous reprsentent deux exemples de fonctions priodiques non sinusodales.
t
f(t)
t
f(t)
T
T
Exemples de fonctions priodiques
Dnition des sries de Fourier Soit f(t) une fonction priodique de priode T, cestdire
telle que f(t) = f(t +T), la srie de Fourier ou le dveloppement de Fourier qui correspond f(t)
est dnie par :
f(t) =
a
0
2
+
n=1
a
n
cos(nt) +b
n
sin(nt)
o = 2/T, n est un entier positif, a
n
et b
n
sont les coecients de Fourier. Ces coecients
sont dnis par les expressions suivantes :
a
n
=
1
T
_
T
0
f(t) cos(nt)dt
b
n
=
1
T
_
T
0
f(t) sin(nt)dt
La valeur a
0
/2 reprsente la valeur moyenne de f(t) sur la priode T. Le terme sinusodal de
pulsation
1
= , la plus faible est appel fondamental tandis que les termes de pulsation
n
= n plus leve sont appels les harmoniques.
Cas des fonctions paires et impaires
Une fonction est dite paire si f(t) = f(t). Dans le cas de dveloppement en srie de
Fourier dune fonction paire,il ny aura que les termes en cosinus et parfois une constante
qui reprsente la valeur moyenne. Il est ais de montrer que :
b
n
= 0
a
n
=
4
T
_ T
2
0
f(t) cos
_
2nt
T
_
dt
Une fonction est dite impaire si f(t) = f(t). Seuls les termes en sinus peuvent trs
prsents dans un dveloppement en srie de Fourier dune fonction impaire. Il est galement
ais de montrer que :
a
n
= 0
b
n
=
4
T
_ T
2
0
f(t) sin
_
2nt
T
_
dt
H. Djelouah
Solution de lquation direntielle La fonction A(t) tant priodique, de priode T, son
dveloppement de Fourier scrit :
A(t) =
a
0
2
+
n=1
a
n
cos(nt) +b
n
sin(nt)
y + 2 y +
2
0
y =
a
0
2
+
n=1
a
n
cos(nt) +b
n
sin(nt)
La rponse permanente ( ou stationnaire ) qui sidentie avec la solution particulire, pour t
susamment lev, peut alors tre calcule pour chacune des composantes de lexcitation : a
0
/2,
a
n
cos(nt), b
n
sin(nt). On obtient alors par superposition :
y(t) =
a
0
2
2
0
+
n=1
a
n
cos(
n
t +
n
) +b
n
sin(
n
t +
n
)
_
(
2
n
2
0
)
2
+ 4
2
2
n
Exercices
Exercice 1 : Calculer et reprsenter graphiquement la solution de lquation direntielle
homogne :
x + 4 x = 0
, pour les conditions initiales suivantes :
1. x(0) = 1 et x(0) = 0.
2. x(0) = 0 et x(0) = 2.
Exercice 2 : Pour les conditions initiales suivantes :
1. x(0) = 1 et x(0) = 0.
2. x(0) = 0 et x(0) = 2.
3. x(0) = 1 et x(0) = 2.
calculer et reprsenter graphiquement les solutions des quations direntielles homognes sui-
vantes :
1. x + 5 x + 4 x = 0
2. x + 4 x + 4 x = 0
3. x + 0.3 x + 4 x = 0
Exercice 3 : Pour les conditions initiales x(0) = 0 et x(0) = 0, calculer et reprsenter graphi-
quement la solution gnrale de chacune des quations direntielles inhomognes suivantes :
1. x + 4x = 5
2. x + 5 x + 4x = 5
3. x + 4 x + 4x = 5
4. x + 0.3 x + 4x = 5
5. x + 4x = 5 cos(3t)
6. x + 4x = 5 cos(2.1t)
7. x + 5 x + 4x = 5 cos(3t
H. Djelouah
8. x + 4 x + 4x = 5 cos(3t)
9. x + 0.3 x + 4x = 5 cos(3t)
Exercice 4 : Calculer la solution particulire de chacune des quations direntielles inhomo-
gnes suivantes :
1. x + 4x = f(t)
2. x + 5 x + 4x = f(t)
3. x + 4 x + 4x = f(t)
o f(t) est une fonction de priode T, dnie par :
_
f(t) = a pour T/2 t 0
f(t) = +a pour 0 t T/2
a tant un nombre rel positif.
H. Djelouah
H. Djelouah
Annexe B
Analogies lectromcaniques
B.1 Introduction
Des systmes mcaniques peuvent tre reprsents par des circuits lectriques analogues.
Deux systmes mcanique et lectrique sont dits analogues si les quations direntielles qui
rgissent leur volution sont identiques. Quand cette quivalence est obtenue, les termes corres-
pondant dans les quations direntielles sont dits analogues.
Il y a deux types danalogies pour les systmes mcaniques et lectriques
lanalogie force-tension ou analogie masse-inductance ; cest la plus utilise.
lanalogie force-courant ou analogie masse-capacitance.
B.2 Analogie force-tension ou masse-inductance
Les relations entre le courant lectrique i et la charge lectrique Q sont exactement de mme
nature que celles qui existent entre la vitesse x et la position x dun systme mcanique en
translation :
i =
dQ
dt
ou encore Q =
_
i dt
x =
dx
dt
ou encore x =
_
xdt
Comme ces grandeurs sont lies par les mmes relations, nous dirons que les grandeurs
lectriques Q et i sont respectivement analogues aux grandeurs mcaniques x et x
x Q
x i
Lorsque le condensateur a emmagasin une charge lectrique Q, la tension lectrique v ses
bornes est donne par la relation :
v =
1
C
Q
Cette relation est de mme nature que celle qui relie lallongement x dun ressort linaire soumis
une force F
F = kx
Nous dirons que la tension lectrique v est analogue une force mcanique et que linverse
de la capacit est analogue un coecient de rappel lastique k :
v F et 1/C k
H. Djelouah
108 Analogies lectromcaniques
Dans le cas dune force de rappel proportionnelle au dplacement x, lnergie potentielle
U(x) est donne par :
U(x) =
1
2
k x
2
Tandis que lnergie c
E
(Q) emmagasine par le champ lectrique dans un condensateur
scrit :
c
E
(Q) =
1
2
Q
2
C
Ces rsultats montrent que lnergie potentielle lastique U(x) est analogue lnergie lec-
trique c
E
(Q) emmagasine dans le condensateur.
Il sut donc de considrer lanalogie : L m pour que la relation v = L
di
dt
soit quivalente
la relation fondamentale de la dynamique
F = m
d x
dt
Tenant compte de ces rsultats, nous pouvons considrer que la quantit lectrique analogue
lnergie cintique est reprsente par lnergie magntique c
M
emmagasine dans la bobine
dauto-inductance :
c
M
=
1
2
L

Q
2
T =
1
2
m x
2
La puissance dissipe sous forme de chaleur dans une rsistance lectrique est donne par la
loi de Joule :
P
J
= Ri
2
La fonction dissipation qui, par dnition, est gale la moiti de la puissance dissipe peut
scrire dans ce cas :
T =
1
2
Ri
2
On remarque quun amortisseur de coecient de frottement visqueux est analogue une
rsistance lectrique : R.
On peut donc tablir le tableau des analogies lectromcaniques suivant :
Mcanique Elctricit
vitesse : x courant : i
force : F d.d.p : v
masse : m inductance : L
amortisseur : rsistance : R
ressort : k capacitance :
1
C
Energie potentielle : U Energie lectrostatique : U
E
Energie cintique : T Energie magntique : U
M
Tableau des analogies force-tension
H. Djelouah
B.3 Systmes un degr de libert 109
B.3 Systmes un degr de libert
Le systme masse-amortisseur-ressort ci-dessus, est rgi par lquation direntielle suivante
m
d
2
x
dt
2
+
dx
dt
+kx = F
Cette quation direntielle peut scrire en fonction de la vitesse x sous la forme
m
d x
dt
+ x +k
_
xdt = F
Lcriture de la seconde loi de Kirchho permet dobtenir lquation direntielle qui rgit
le circuit R.L.C srie ci-dessus
L
di
dt
+Ri +
1
C
_
i dt = e
Les quations direntielles qui rgissent ces deux systmes sont de mme nature. Les deux
systmes physiques sont dits analogues.
B.4 Systme deux degrs de libert
Exercice rsolu
Etablir, dans le cadre de lanalogie force-tension, le systme lectrique analogue au systme
mcanique deux degrs de libert ci-dessous.
H. Djelouah
Solution
Seule une dmarche mthodique permet dobtenir le circuit lectrique analogue. Les di-
rentes tapes sont
1. Etablir le systme dquations direntielles
m
1
x
1
+ (
1
+
2
) x
1
+ (k
1
+k
2
) x
1
2
x
2
k
2
x
2
= F
m
2
x
2
+
2
x
2
+k
2
x
2
2
x
1
k
2
x
1
= 0
2. Regrouper les dirents termes en mettant en facteur chaque grandeur correspondant
un lment mcanique.
m
1
x
1
+
1
x
1
+k
1
x
1
+
2
( x
1
x
2
) +k
2
(x
1
x
2
) = F
m
2
x
2
2
( x
1
x
2
) k
2
(x
1
x
2
) = 0
3. Ecrire le systme dquations direntielles sous la forme dun systme intgro-direntiel
m
1
d x
1
dt
+
1
x
1
+k
1
_
x
1
dt +
2
( x
1
x
2
) +k
2
_
( x
1
x
2
) dt = F
m
2
d x
2
dt

2
( x
1
x
2
) k
2
_
( x
1
x
2
) dt = 0
4. Etablir la liste des lments lectriques analogues
Mcanique Electricit
x
1
i
1
x
2
i
2
m
1
L
1
m
2
L
2
k
1
1
C
1
k
2
1
C
2
1
R
1
2
R
2
F e
H. Djelouah
B.4 Systme deux degrs de libert 111
5. Remplacer chaque terme du systme dquations mcanique par un terme lectrique ana-
logue. Ce qui permet dtablir le systme dquations intgro-direntiel lectrique
L
1
di
1
dt
+R
1
i
1
+
1
C
1
_
i
1
dt +R
2
(i
1
i
2
) +
1
C
2
_
(i
1
i
2
) dt = e
L
2
di
2
dt
R
2
(i
1
i
2
)
1
C
2
_
(i
1
i
2
) dt = 0
6. Construire le circuit lectrique analogue en remarquant que les termes de ces deux qua-
tions sont respectivement la d.d.p aux bornes de L
1
, R
1
, C
1
, R
2
, C
2
, e et L
2
. Ces deux
quations rprsentent lcriture de la seconde loi de Kircho pour deux mailles parcourues
respectivement par les courants i
1
et i
2
et qui ont une branche commune contenant R
2
et
C
2
et parcourue par le courant i = i
1
i
2
.
H. Djelouah
H. Djelouah
Bibliographie
[1] Crawford, F. S., Berkeley : Cours de physique : Ondes, Volume 3, Dunod, 1999.
[2] Gabillard, R., Vibrations et phnomnes de propagation, Dunod, Paris, 1969.
[3] Kelly, S. G., Shaums outline of theory and problems of mechanical vibrations, McGraw
Hill, 1996.
[4] Kinsler, L. E., Fundamentals of acoustics, Wiley, 2000.
[5] Rocard, Y., Dynamique gnrale des vibrations (4me d.), Masson, Paris, 1971.
[6] Roseau, M., Vibrations des systmes mcaniques, Masson, Paris, 1984.
[7] Salles, F., Lesueur, C., Les vibrations mcaniques, Masson, Paris, 1972.
[8] Seto, W. W., Schaums outline of theory and problems of acoustics, McGraw-Hill, 1971
[9] Soutif, M., Vibrations, propagation, diusion, Dunod, Paris, 1970.
[10] Steidel, R. F., An Introduction to mechanical vibrations, (2nd ed), J. Wiley and Sons, 1980.
[11] Thomson, W.T., Theory of vibrations with applications (2nd d.), Prentice-Hall, 1981.
[12] Timoshenko, S., Thorie des vibrations, Branger, Paris, 1954.
[13] Timoshenko, S., Young, D. H., Weaver, W. , Vibration Problems in Engineering (4th d.),
J. Wiley and Sons, N. Y., 1974 (dition anglaise de louvrage ci-dessus).
[14] Tse, F. S., Morse, I. E., Minkle, R.T., Mechanical vibrations (2nd d.), Allyn & Bacon,
1978.
H. Djelouah

Cours Vom Djelouah PDF

Transféré par

Informations du document

Titre original

Copyright

Formats disponibles

Partager ce document

Partager ou intégrer le document

Options de partage

Avez-vous trouvé ce document utile ?

Ce contenu est-il inapproprié ?

Droits d'auteur :

Formats disponibles

Cours Vom Djelouah PDF

Transféré par

Droits d'auteur :

Formats disponibles

V

2. A cette pulsation, appele pulsation de rsonance, on

Le dterminant () est appel dterminant caractristique. Lquation () = 0 est appe-

Les variations des amplitudes X

est la priode temporelle tandis que la quantit = V T est la longueur

est appel le module du vecteur donde qui sexprime en m

nest pas ncessairement la vitesse que lon observe lorsquon analyse

OM, la quantit s dpend du temps et du vecteur

qui a la dimension dune vitesse, on constate que :

est le module du vecteur donde, tant la longueur donde.

o G est le module de cisaillement ; il sexprime galement en N m

est le module du vecteur donde, tant la longueur donde.

E est limpdance caractristique du matriau constituant le barreau.

< 1, la frquence des ondes lastiques pouvant se propager dans un cristal

A, la frquence de coupure est

et la phase de londe rchie.

et dun amortisseur de coecient de frottement visqueux (Figure b). On

et pour quil ny ait pas donde rchie.

9.3 Vitesse du son

Vous aimerez peut-être aussi