Académique Documents
Professionnel Documents
Culture Documents
11 Fiche Inegalites Classiques - Eleve
Transféré par
deededTitre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
11 Fiche Inegalites Classiques - Eleve
Transféré par
deededDroits d'auteur :
Formats disponibles
Lycée Kléber PC⋆ 2ième année
F ICHE : I NÉGALITÉS CLASSIQUES
Fonctions usuelles
x3
∀x Ê 0, x− É sin x É x
6
¯ ¯ ¯ ¯
∀(x, y) ∈ R2 , ¯sin x − sin y ¯ É ¯ x − y ¯
h πh 2
∀x ∈ 0, , x É sin x É x É tan x
Avec des identités remarquables 2 π
x2
Pour a, b ∈ R : ∀x ∈ R, 1− É cos x É 1
2
x2
4ab É (a + b)2 ∀x ∈ R, |cos x − 1| É
2
(a + b)2 É 2(a 2 + b 2 )
∀x Ê 0, arctan x É x
2|ab| É a 2 + b 2 x2
p p p ∀x Ê 0, x− É ln(1 + x) et ∀x > −1, ln(1 + x) É x
a + b É a + b si a, b Ê 0 2
1 + nx É (1 + x)n pour x > −1 (Inégalité de Bernoulli) ∀x > 0, ln x < x
||a| − |b|| É |a + b| É |a| + |b| (Inégalités triangulaires) ∀x ∈ R, 1 + x É ex
∀x Ê 0, sh x Ê x
x2
∀x ∈ R, ch x Ê 1 +
2
Inégalités de Cauchy-Schwarz et applications
Inégalité des accroissement finis - Version I
Dans un préhilbertien (E, 〈.|.〉), pour tout x, y ∈ E on a :
Soit f : [a, b] → R. On suppose que :
¯ ¯ ° °
¯〈x|y〉¯ É kxk ° y °
H1 f est continue sur [a, b]
avec égalité si et seulement si x et y sont colinéaires. H2 f est dérivable sur ]a, b[
Il en résulte que : ¯ ¯ s
¯Xn ¯ n
s
n H3 Il existe (m, M) ∈ R2 tel que :
X 2
X
2n
b i2 ;
¯ ¯
• ∀(a1 , . . . , an , b 1 , . . . , b n ) ∈ R , ¯ ai b i ¯ É ai
m É f ′ (x) É M
¯i=1 ¯ i=1 i=1
¯ qR ¯ ∀x ∈]a, b[,
¯R
¯ b b¯ ¯2 qRb ¯ ¯2
• ∀f , g ∈ C 0 ([a, b] , C) , ¯ a f (t )g (t ) dt ¯ É ¯ dt
a g (t ) d t ;
¯
a f (t ) ¯ ¯
¯R ¯ Alors on a :
• Pour toutes fonctions f , g continues et de carré intégrable sur I : ¯ I f (t )g (t ) dt ¯ É
qR ¯ ¯2 q R¯ ¯2 m (b − a) É f (b) − f (a) É M (b − a)
I f (t ) d t I g (t ) d t ;
¯ ¯ ¯ ¯
Inégalité des accroissement finis - Version II
Soit f : [a, b] → R. On suppose que :
H1 f est continue sur [a, b]
Z+∞ +∞
X Z+∞
H2 f est dérivable sur ]a, b[ f (t ) dt É f (k) É f (t ) dt
a+1 k=a+1 a
¯ ′¯ ¯ ′ ¯
H3 ¯ f ¯ est majorée sur ]a, b[ : ∃α ∈ R+ : ∀x ∈]a, b[, ¯ f (x)¯ É α
f (k)
Alors on a : ¯ ¯ ¯ ¯
¯ f (b) − f (a)¯ É sup ¯ f ′ (x)¯ |b − a|
k −1 k k +1
x∈]a,b[
Critère spécial des séries alternées (TSA)
P
Inégalité de Taylor-Lagrange On considère une série (−1)n v n .
| {z }
un
Soit f une fonction de classe C n+1 sur un intervalle I de R et soit a ∈ I. Si x ∈ I, on peut,
d’après la formule de Taylor avec reste intégrale, écrire f (x) sous la forme H1 À partir d’un certain rang v n Ê 0.
La suite (v n ) est décroissante à partir d’un certain rang.
n f (k) (a) Zx
X k (x − t )n (n+1) H2
f (x) = (x − a) + f (t ) dt
k=0 k! a n!
H3 v n −−−−−→ 0
= Tn (x) + Rn (x) n→+∞
Alors :
On a alors 1. la série alternée
P
(−1)n v n converge ;
+∞
X
n+1
¯ f (x) − Tn (x)¯ = |Rn (x)| É |x − a|
¯ ¯
Mn+1 2. On dispose d’une majoration du reste Rn = (−1)n v n par la valeur absolue du
(n + 1)! k=n+1
premier terme négligé |un+1 | :
¯ ¯ |Rn | É v n+1
où Mn+1 est un majorant de ¯ f (n+1) ¯ sur [a, x] (qui existe car f (n+1) est continue sur le segment
[a, x])
3. Le signe du reste Rn est le même que celui du premier terme négligé : sg(Rn ) =
sg(un+1 ).
Comparaison séries-intégrales
4. En notant respectivement S et S n la somme et la nième somme partielle de la série,
Soit f : [a, +∞[7→ R une fonction continue par morceaux (a ∈ N ). On suppose que : comme (S 2n ) est décroissante, que (S 2n+1 ) est décroissante et que pour tout n ∈ N,
H1 f est à valeurs positives. S 2n+1 É S É S 2n , on a les inégalités sur les sommes partielles :
H2 f est décroissante. S 1 É S 3 É . . . É S 2n+1 É . . . É S É . . . É S 2n É . . . É S 2 É S 0 .
¡R ¢
Alors la série f (n) et la suite an f (t ) dt sont de même nature. De plus, si elles convergent :
P
Vous aimerez peut-être aussi
- 10 Fiche Inegalites Classiques EleveDocument2 pages10 Fiche Inegalites Classiques EleveABDELMOGHIT IDHSAINEPas encore d'évaluation
- Serie Trigonométrie 1S1 Axlou Toth Renf FinalDocument9 pagesSerie Trigonométrie 1S1 Axlou Toth Renf FinalKANDEPas encore d'évaluation
- Cahier de TextesDocument9 pagesCahier de Textesgenie RyodanePas encore d'évaluation
- 1594879511Document16 pages1594879511achrafPas encore d'évaluation
- 3 Etudes de FonctionsDocument22 pages3 Etudes de FonctionsKakou Light MalanPas encore d'évaluation
- Devoir Maison N3 2emeBAC S2Document2 pagesDevoir Maison N3 2emeBAC S2Badiane MamadouPas encore d'évaluation
- Examen SR (2018 19)Document2 pagesExamen SR (2018 19)Elmehdi TalbiPas encore d'évaluation
- Cours D Arithmétique DébutantDocument28 pagesCours D Arithmétique DébutantTamaru DialloPas encore d'évaluation
- PC - Corriges Et Bareme Bac Blanc Serie DDocument4 pagesPC - Corriges Et Bareme Bac Blanc Serie DSarah DiomandePas encore d'évaluation
- Cours de Maths Tle D Apc Ecole OnlineDocument194 pagesCours de Maths Tle D Apc Ecole OnlineLadjale MaxPas encore d'évaluation
- Derivee Lecture Graphique 3Document2 pagesDerivee Lecture Graphique 3Camara laye100% (1)
- TD Maths Leçon 12 Equations DifférentiellesDocument7 pagesTD Maths Leçon 12 Equations Différentiellessiaka sanogoPas encore d'évaluation
- Exercices Angles OrientesDocument2 pagesExercices Angles OrientesjosuemanueljsmPas encore d'évaluation
- Mouvements Plans Resume de Cours 1 1Document3 pagesMouvements Plans Resume de Cours 1 1Najimou Alade TidjaniPas encore d'évaluation
- Controle 2 GastliDocument2 pagesControle 2 GastlitorkitaherPas encore d'évaluation
- Leçon 1 Calcul LittéralDocument10 pagesLeçon 1 Calcul LittéralDieu Est FidèlePas encore d'évaluation
- 4.Sc.C.1.FN 12.13Document3 pages4.Sc.C.1.FN 12.13Mohamed SaidiPas encore d'évaluation
- 1S 03 PRODUIT - SCALAIRE CoursDocument11 pages1S 03 PRODUIT - SCALAIRE Coursمحمذن علي اكاه100% (1)
- Bac 19 DDocument3 pagesBac 19 DDieu Est Fidèle100% (1)
- Corrige Manuel Scolaire 3 Math Section Math t2Document240 pagesCorrige Manuel Scolaire 3 Math Section Math t2Mariem Nejima100% (1)
- Chapitre 7 Cours Vecteurs Seconde 1ere PartieDocument2 pagesChapitre 7 Cours Vecteurs Seconde 1ere PartieCamara layePas encore d'évaluation
- Multiples Division Euclidienne Congruence Exercices Non CorrigesDocument7 pagesMultiples Division Euclidienne Congruence Exercices Non CorrigesHassan ElouardiPas encore d'évaluation
- Exercices DérivabilitéDocument4 pagesExercices DérivabilitéLOUNDOU orthegaPas encore d'évaluation
- Etude Des Fonctions Cours Et Exercices CorrigesDocument16 pagesEtude Des Fonctions Cours Et Exercices CorrigesSoumana100% (1)
- Les Suites Exe Corr SexDocument9 pagesLes Suites Exe Corr Sexniangfatma64Pas encore d'évaluation
- Cours TCD Complet 145 PagesDocument145 pagesCours TCD Complet 145 PagesPrincicø Law leungPas encore d'évaluation
- Fax TDDocument40 pagesFax TDjpwhwdpbytPas encore d'évaluation
- TD 02 2nde MATHSDocument2 pagesTD 02 2nde MATHSDjalalou-Dine MEMOKOPas encore d'évaluation
- De Cuong Hoc Ki 2 Lop 11 Mon Toan de Cuong Hk2 Lop 11 Chuan Theo Yeu Cau BDGDocument5 pagesDe Cuong Hoc Ki 2 Lop 11 Mon Toan de Cuong Hk2 Lop 11 Chuan Theo Yeu Cau BDGKiên TrungPas encore d'évaluation
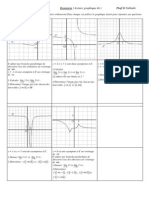
- Lecture Graphique de Limite 1Document1 pageLecture Graphique de Limite 1gfgfgfgfgfgfgfgfgfgfPas encore d'évaluation
- TDMeca 5Document3 pagesTDMeca 5Ihsan Mokhlisse100% (1)
- Situation Complexe Maths Tle D 20102021Document16 pagesSituation Complexe Maths Tle D 20102021DadiéPas encore d'évaluation
- Série de Rappel Sur Les Limites Bac SC MathsDocument4 pagesSérie de Rappel Sur Les Limites Bac SC Mathspaul pl j,labdihbPas encore d'évaluation
- Serie 11 1 Bac SCM La Dérivation 1Document3 pagesSerie 11 1 Bac SCM La Dérivation 1Taha KarmimPas encore d'évaluation
- Élève L'amplificateur OperationnelDocument3 pagesÉlève L'amplificateur OperationnelFélix KouassiPas encore d'évaluation
- DS1 2bacDocument2 pagesDS1 2bacMaster MathPas encore d'évaluation
- TD 5 SolutionDocument8 pagesTD 5 Solutionsid ali saidjPas encore d'évaluation
- QCM 2451 Fonctions Homographiques CorrDocument2 pagesQCM 2451 Fonctions Homographiques Corrapi-203629011Pas encore d'évaluation
- IntégrationDocument27 pagesIntégrationibouPas encore d'évaluation
- Partiel Analyse2 2016corrigeDocument5 pagesPartiel Analyse2 2016corrigehichem benbouPas encore d'évaluation
- DS8 PsiDocument5 pagesDS8 Psiourrslim78Pas encore d'évaluation
- Enoncé Analyse - MP1Document2 pagesEnoncé Analyse - MP1Sa Majesté DavidPas encore d'évaluation
- Série 4 Ordre Opérations 2APIC CorrigéDocument2 pagesSérie 4 Ordre Opérations 2APIC Corrigéخطوة خطوة100% (1)
- Décomposition en Éléments Simples Des Fractions RationnellesDocument4 pagesDécomposition en Éléments Simples Des Fractions RationnellesImmamHadramy100% (1)
- Devoir de Synthèse N°1 - Math - 3ème Mathématiques (2010-2011) MR Mechmeche ImedDocument2 pagesDevoir de Synthèse N°1 - Math - 3ème Mathématiques (2010-2011) MR Mechmeche ImedRami Ben HjalPas encore d'évaluation
- V2 Les Vecteurs Exercices Chasles-Demonstration PDFDocument3 pagesV2 Les Vecteurs Exercices Chasles-Demonstration PDFWan Theo100% (1)
- Exam2021 - 11 - Final RecupereDocument7 pagesExam2021 - 11 - Final RecupereLamine BayoPas encore d'évaluation
- Serie Developpements LimitesDocument1 pageSerie Developpements LimitesiVictoriousPas encore d'évaluation
- TD5 (Complexes Nationaux)Document14 pagesTD5 (Complexes Nationaux)john marstonPas encore d'évaluation
- Resolution NumeriqueDocument5 pagesResolution Numeriqueanas achmitPas encore d'évaluation
- Devoir Surveillé N°5: Nombre DérivéDocument2 pagesDevoir Surveillé N°5: Nombre DérivéJohan Faber100% (1)
- Blanc8 BacDocument7 pagesBlanc8 Bacmister633Pas encore d'évaluation
- Equationsdegre2Exoscorriges PDFDocument4 pagesEquationsdegre2Exoscorriges PDFBalalaŇaŖîfPas encore d'évaluation
- Série Des Exercices de Renforcements Pour Chapitre 03 Les ApplicationsDocument2 pagesSérie Des Exercices de Renforcements Pour Chapitre 03 Les ApplicationsBadre-eddine FriferPas encore d'évaluation
- Cours Math - Arithmétique Divisibilité Ans Z - Bac Math (2009-2010) MR Abdelbasset LaataouiDocument4 pagesCours Math - Arithmétique Divisibilité Ans Z - Bac Math (2009-2010) MR Abdelbasset LaataouiSami KetataPas encore d'évaluation
- TD4 Fonctions Trigonom Triques Et Hyperboliques Inverses 100538Document2 pagesTD4 Fonctions Trigonom Triques Et Hyperboliques Inverses 100538Areh yare abwan somaliyed100% (1)
- Correction Series TD1 PDFDocument28 pagesCorrection Series TD1 PDFanon_441994392Pas encore d'évaluation
- Derive 1Document5 pagesDerive 1Samba Sall100% (2)
- Formulaire ScientifiqueDocument12 pagesFormulaire ScientifiqueOussama ElfaqyrPas encore d'évaluation
- Corrige Maths Bce Edhec 2020Document8 pagesCorrige Maths Bce Edhec 2020Diomande WilfriedPas encore d'évaluation