Académique Documents
Professionnel Documents
Culture Documents
Corrigé Sujet 6
Transféré par
Victor DeschampsTitre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
Corrigé Sujet 6
Transféré par
Victor DeschampsDroits d'auteur :
Formats disponibles
; Corrigé du baccalauréat Polynésie 2 juin 2021 <
ÉPREUVE D’ENSEIGNEMENT DE SPÉCIALITÉ no 2
E XERCICE 1 5 points
Commun à tous les candidats
On considère la suite (u n ) définie par u 0 = 10 000 et pour tout entier naturel n :
u n+1 = 0, 95u n + 200.
1. • u 1 = 0, 95 × u 0 + 200 = 0, 95 × 10 000 + 200 = 9 500 + 200 = 9 700.
• u 2 = 0, 95 × u 1 + 200 = 0, 95 × 9 700 + 200 = 9 215 + 200 = 9 415.
2. a. On démontre par récurrence, que pour tout entier naturel n : u n > 4 000.
Initialisation : u 0 = 10 000 > 4 000 : l’inégalité est vraie au rang 0 ;
Hérédité : supposons que pour n ∈ N, on ait u n > 4 000, alors par produit par
0, 95 > 0, on a 0, 95u n > 0, 95 × 4 000, soit :
0, 95u n > 3 800, et en ajoutant 200 à chaque membre :
0, 95u n + 200 > 3 800 + 200, c’est-à-dire u n+1 > 4 000 : la relation est vraie au rang
n + 1.
Conclusion : l’inégalité est vraie au rang 0 et si elle est vraie au rang n ∈ N, elle est
vraie au rang n + 1 : d’après le principe de récurrence u n > 4 000 quel que soit le
naturel n.
b. On sait que si la suite est décroissante et minorée par 4 000, elle converge vers
une limite ℓ, avec ℓ > 4 000.
3. a. Pour n = 0, on a v 0 = u 0 − 4 000 = 10 000 − 4 000 = 6 000.
b. Au choix :
Méthode 1 : pour n ∈ N, on a :
µ ¶
3 800
v n+1 = u n+1 − 4 000 = 0, 95u n + 200 − 4 000 = 0, 95u n − 3 800 = 0, 95 u n − =
0, 95
0, 95 (u n − 4 000) = 0, 95v n .
L’égalité v n+1 = 0, 95v n vraie quel que soit n ∈ N montre que la suite (v n ) est géo-
métrique de raison égale à 0, 95.
Méthode 2 : pour n ∈ N, on a vu que u n > 4 000, donc v n = u n − 4000 > 0.
v n+1 u n+1 − 4 000 0, 95u n + 200 − 4 000
On peut donc calculer : = = =
vn u n − 4³ 000 ´ u n − 4 000
0, 95u n − 3 800 0, 95u n − 3 800 0,95 un − 30,95
800
0, 95 (u n − 4 000)
= = un −4 000 = = 0, 95.
u n − 4 000 u n − 4 000 u n − 4 000
Cette égalité vraie pour tout naturel n, montre que la suite (v n ) est géométrique
de raison égale à 0, 95.
c. D’après le résultat précédent, on sait que que pour tout n ∈ N,
v n = v 0 × 0, 95n = 6 000 × 0, 95n .
Or v n = u n − 4 000 ⇐⇒ u n = v n + 4 000 = 6 000 × 0, 95n + 4 000.
d. Comme 0 < 0, 95 < 1, on sait que lim 0, 95n = 0, donc lim 6 000 × 0, 95n = 0,
n→+∞ n→+∞
d’où lim u n = 4 000 (par somme de limites).
n→+∞
Corrigé du baccalauréat spécialité A. P. M. E. P.
4. u n est égal au nombre d’individus de l’espèce animale au rang n ; d’après le résultat
précédent ce nombre va diminuer et se rapprocher de 4 000 soit moins de la moitié de
la population initiale : le responsable a raison.
E XERCICE 2 5 points
Commun à tous les candidats
1. On construit un arbre pondéré modélisant la situation proposée :
0,8 T
0,07 M
0,2 T
0,01 T
0,93 M
0,99 T
2. a. On a P (M ∩ T ) = P (M ) × P M (T ) = 0, 07 × 0, 8 = 0, 056.
³ ´ ³ ´
b. On a de même P M ∩ T = P M × P M (T ) = 0, 93 × 0, 01 = 0,009 3.
D’après la loi des probabilités totales :
³ ´
P (T ) = P (M ∩ T ) + P M ∩ T = 0, 056 + 0,009 3 = 0,065 3.
P (T ∩ M ) P (M ∩ T ) 0, 056
3. On calcule P T (M ) = = = ≈ 0,857 58 soit 0, 86 à 10−2 près.
P (T ) P (T ) 0,065 3
4. a. X suit une loi binomiale de paramètres n = 10 avec p = 0,065 3.
b. On a P (X = 2) = 10 2 10−2
= 10 2 8
¡ ¢ ¡ ¢
2 × 0,065 3 × (1 − 0,065 3) 2 × 0,065 3 × 0, 9347 =
45 × 0,065 32 × 0, 93478 ≈ 0,111 8, soit 0, 11 à 10−2 près.
5. On a P (X > 1) = 1 − P (X = 0) = 1 − n0 × 0,065 30 × (1 − 0,065 3)n = 1 − 0,934 7n et on veut
¡ ¢
que :
P (X > 1) > 0, 99 ⇐⇒ 1 − 0,934 7n > 0, 99 ⇐⇒ 0, 01 > 0,934 7n soit en prenant le loga-
rithme népérien :
ln 0, 01
ln 0, 01 > n ln 0,934 7 ⇐⇒ < n.
ln 0,934 7
ln 0, 01
Or ≈ 68, 2.
ln 0,934 7
Il faut donc tester au moins 69 personnes au minimum.
E XERCICE 3 5 points
Commun à tous les candidats
Polynésie 2 2 juin 2021
Corrigé du baccalauréat spécialité A. P. M. E. P.
H
F
M b
B D
y
x
C
³ −−→ −−→ −→´
1. Dans le repère A ; AB , AD , AE , on a
B(1 ; 0 ; 0), D(0 ; 1 ; 0), E(0 ; 0 ; 1), G(1 ; 1 ; 1), H(0 ; 1 ; 1).
2. a. [EG], [GD] et [ED] sont les hypoténuses de triangles rectangles isocèles de côté 1,
p
donc EG = GD = ED = 2 : le triangle EGD est équilatéral.
p p p
p 3 ¡p ¢2 3 3
b. Puisque c = 2, on a A (EGD) = × 2 = ×2 = .
4 4 2
1
−1 −3 xM − 1
−−→ −−→ 1 −−→
3. On a BH 1 , donc BM = BH 13 = y M − 0.
3
1 1 zM − 0
3
1 2 1 1
On a donc : x M = 1 − = ; y M = ; z M = .
3 3 3 µ 3 ¶
2 1 1
Conclusion : M a pour coordonnées ; ; .
3 3 3
1
−−→ →
− −−→
4. a. On a EG 1 : donc n · EG = −1 + 1 + 0 = 0 :
0
0
−−→ →
− −−→
ED 1 : donc n · ED = 0 + 1 − 1 = 0.
−1
→
−
Conclusion : n est orthogonal à deux vecteurs non colinéaires du plan (EGD) :
c’est un vecteur normal à ce plan.
b. On sait qu’un plan d’équation ax + b y + c z + d = 0 a un vecteur normal de coor-
données (a ; b ; c), donc :
P (x ; y ; z) ∈ (EGD) ⇐⇒ −x + y + z + d = 0.
Comme E(0 ; 0 ; 1)∈ (EGD) ⇐⇒ 0 + 0 + 1 + d = 0 ⇐⇒ d = −1.
Finalement : le plan (EGD) a pour équation −x + y + z − 1 = 0.
Polynésie 3 2 juin 2021
Corrigé du baccalauréat spécialité A. P. M. E. P.
→
−
c. La droite D contient M et a pour vecteur directeur n vecteur normal au plan
x − 23
−−→
(EGD), donc avec MP y − 23 :
z − 13
−−→ →
−
P (x ; y ; z) ∈ D ⇐⇒ MP = t n , avec t ∈ R, soit :
2 2
x − 3 = −t
x = 3 −t
y − 13 = t , t ∈ R ⇐⇒ y = 31 + t , t ∈ R.
z − 13 = t z = 13 + t
5. Le cube ABCDEFGH est représenté ci-dessus selon une vue qui permet de mieux per-
cevoir la pyramide GEDM, en gris sur la figure :
G z
F
H
E
x
C M
B
y
D
A
a. On a vu que la droite D contient M et est perpendiculaire au plan (EBD) : c’est
donc la hauteur de la pyramide GEDM issue de M. Le pied de cette hauteur K
appartient donc à D et au plan (EGD) ; ses coordonnées vérifient donc les équa-
tions :
= 32 − t
x
y = 31 + t
⇒ − 32 − t + 31 +t + 13 +t −1 = 0 ⇐⇒ 3t = 1 ⇐⇒ t = 13 .
¡ ¢
1
z = 3 +t
−x + y + z − 1 = 0
1
En remplaçant t par 3
dans l’équation paramétrique de D, on obtient :
2 1 1
x = 3−3=3
y = 13 + 13 = 23
z = 13 + 13 = 23
¶ µ
1 2 2
Conclusion : K a pour coordonnées ; ; .
3 3 3
Polynésie 4 2 juin 2021
Corrigé du baccalauréat spécialité A. P. M. E. P.
1
3
−−→ 1
b. On en déduit KM − 3 .
− 13
p
1 1 1 3
2 3
D’où KM = + + = ; on en déduit KM= .
9 9 9 9 3 p p
p 3 3
3 2 × 3 1
Comme A (EGD) = 2
, le volume de la pyramide GEDM est : = .
3 6
EXERCICE au choix du candidat 5 points
EXERCICE A
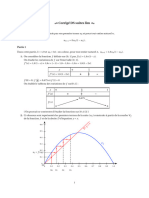
y
3
C A
2
B
−3 −2 −1 0 1 2 3
x
Partie 1
1. • A a pour ordonnée f (0) = 2 ;
y B − y A 0 − 2 −2
• Le nombre dérivé f ′ (0) = = = = −1.
xB − xA 2 − 0 2
2. La fonction f semble convexe sur l’intervalle ] − ∞ ; 0].
Partie 2
On note (E ) l’équation différentielle : y ′ = −y + e−x .
1. On sait que les solutions de l’équation (H ) : y ′ = −y sont les fonctions x 7−→ K e−x , avec
K ∈ R.
2. Les solutions de l’équation (E ) sont donc les fonctions
x 7−→ xe−x + K e−x = (x + K )e−x , K ∈ R.
Polynésie 5 2 juin 2021
Corrigé du baccalauréat spécialité A. P. M. E. P.
3. Avec f (x) = (x + K )e−x et f (0) = 2, on a : (0 + K )e−0 = 2 ⇐⇒ K = 2.
Conclusion : f (x) = (x + 2)e−x .
Partie 3
1. a. Puisque f est solution de l’équation différentielle (E ) ; on a donc
f ′ (x) = − f (x) + e−x = −(x + 2)e−x + e−x = e−x (−x − 2 + 1) = (−x − 1)e−x .
b. Comme quel que soit x ∈ R, e−x > 0, le signe de f ′ (x) est celui de −x − 1. Donc :
−x − 1 > 0 ⇐⇒ −1 > x ⇐⇒ x < −1 ;
−x − 1 < 0 ⇐⇒ −1 < x ⇐⇒ x > −1 ;
−x − 1 = 0 ⇐⇒ −1 = x.
La fonction est donc croissante sur ] − ∞ ; −1[, décroissante sur ] − 1 ; +∞[ et a
donc un maximum f (−1) = (−1 + 2)e−(−1) = e.
2. a. De f ′ (x) = − f (x) + e−x , on obtient en dérivant :
f ′′ (x) = − f ′ (x) − e−x = −(−x − 1)e−x − e−x = e−x (x + 1 − 1) = xe−x .
b. D’après le résultat précédent sur [0 ; +∞[, x > 0 et e−x > 0, donc le produit
xe−x > 0 : la dérivée seconde est positive, la fonction f est convexe sur [0 ; +∞[.
EXERCICE B
Partie 1 : Étude d’une fonction auxiliaire
Soit la fonction f définie sur l’intervalle [1 ; 4] par : f (x) = −30x + 50 + 35 ln x.
35 −30x + 35 35 − 30x
1. a. Sur l’intervalle [1 ; 4], f ′ (x) = −30 +
= = .
x x x
b. Puisque 1 6 x 6 4, x > 0, donc le signe de f ′ (x) est celui du numérateur 35 −
30x = 5(7 − 6x) donc du facteur 7 − 6x.
7 7
7 − 6x > 0 ⇐⇒ 7 > 6x ⇐⇒ > x ⇐⇒ x < ;
6 6
7 7
7 − 6x < 0 ⇐⇒ 7 < 6x ⇐⇒ <> x ⇐⇒ x > ;
6 6
7 7
7 − 6x = 0 ⇐⇒ 7 = 6x ⇐⇒ = x ⇐⇒ x = .
6 6
· ¸ · ¸
7 7
c. La fonction f est donc croissante sur 1 ; , décroissante sur ; 4 et a donc
µ ¶ 6 6
7 7 7 7 7
un maximum : f = −30 × + 50 + 35 ln = −35 + 50 + 35 ln = 15 + 35 ln ≈
6 6 6 6 6
20, 4.
· ¸ µ ¶
7 7 7
2. f décroit sur ; 4 de f = 15+35 ln ≈ 20, 4 à f (4) = −120+50+35 ln 4 = 35 ln 4−
6 6 6
70 ≈ −21, 5.
Polynésie 6 2 juin 2021
Corrigé du baccalauréat spécialité A. P. M. E. P.
7
x 1 6 α 4
≈ 20, 4
f 0
20 ≈ −21, 4
· ¸
7
Sur l’intervalle ; 4 , f est continue et strictement décroissante.
6
£ ¡7¢ ¤
Comme 0 ∈ f 6 ; f (4) , il existe d’après le théorème des valeurs intermédiaires, un
réel unique α de cet intervalle tel que f (α) = 0.
• On a f (2) ≈ 14, 26 et f (3) ≈ −1, 54, donc 2 < α < 3 ;
• On a f (2, 9) ≈ 0, 26 et f (3, 0) ≈ −1, 54, donc 2, 9 < α < 3, 0 ;
• On a f (2, 91) ≈ 0, 09 et f (2, 92) ≈ −0, 09, donc 2, 91 < α < 2, 92 ;
• On a f (2, 914) ≈ 0, 0013 et f (2, 915) ≈ −0, 005, donc 2, 914 < α < 2, 915.
3. On a donc f (x) > 0 sur [1 ; α] et f (x) 6 0 sur [α ; 4].
Partie 2 : Optimisation
B (x) = −15x 2 + 15x + 35x ln x.
1. 2 500 litres correspondent à x = 2, 5 et B (2, 5) = −15 × 2, 52 + 15 × 2, 5 + 35 × 2, 5 × ln 2, 5 ≈
23,925 4 soit environ 23 925 (.
2. La fonction B est dérivable sur [1 ; 4] et sur cet intervalle :
1
B ′ (x) = −30x + 15 + 35 ln x + 35x × = 50 − 30x + 35 ln x = f (x).
x
3. a. D’après la partie 1, f (x) = B ′ (x) > 0 sur [1 ; α] : la fonction B est donc croissante
sur [1 ; α].
De même f (x) = B ′ (x) 6 0 sur [α ; 4] : la fonction B est donc décroissante sur
[1 ; α].
Conclusion : B (α) est le maximum de la fonction B sur l’intervalle [1 ; 4].
b. B (α) = −15α2 + 15α + 35α ln α.
En utilisant la valeur approchée de α trouvée dans la partie 1, on a :
B (α) ≈ −15 × 2, 9142 + 15 × 2, 914 + 35 × 2, 914 × ln 2, 914 ≈ 25, 4201, soit environ
25 420 ( à l’euro près.
Il faut donc que l’entreprise vende 2 914 litres de jus de fruits pour faire un béné-
ficie maximal.
Polynésie 7 2 juin 2021
Vous aimerez peut-être aussi
- PDF Livre Etude 50 Cles Pour Vivre Avec Les AngesDocument272 pagesPDF Livre Etude 50 Cles Pour Vivre Avec Les AngesOL80% (5)
- Équations différentielles: Les Grands Articles d'UniversalisD'EverandÉquations différentielles: Les Grands Articles d'UniversalisPas encore d'évaluation
- Les Figures de Style Cours Et ExercicesDocument5 pagesLes Figures de Style Cours Et ExercicesadelkamelPas encore d'évaluation
- Mobile 1 Niv.a1 - Livre + CD Audio + DVD-2278076558Document4 pagesMobile 1 Niv.a1 - Livre + CD Audio + DVD-2278076558ali0% (1)
- Oral CAPES Math 2012: Lecon 10 - EchantillonageDocument7 pagesOral CAPES Math 2012: Lecon 10 - EchantillonageClément BoulonnePas encore d'évaluation
- TD1 CorrigeDocument5 pagesTD1 Corrigetamba vieux tolnoPas encore d'évaluation
- Ross Anne - Les Plus Belles Légendes Des CeltesDocument129 pagesRoss Anne - Les Plus Belles Légendes Des CeltesLimogesGadesPas encore d'évaluation
- Al7ma02tdpa0112 Sequence 01Document60 pagesAl7ma02tdpa0112 Sequence 01eli0t3zPas encore d'évaluation
- Bilan Sur L'histoire LittéraireDocument11 pagesBilan Sur L'histoire LittéraireCherif ChokeirPas encore d'évaluation
- 18 Les Suites NumériquesDocument7 pages18 Les Suites NumériqueslvtmathPas encore d'évaluation
- Corrige S AmeriqueNord Juin 2021 DVDocument7 pagesCorrige S AmeriqueNord Juin 2021 DVpablitorock2006Pas encore d'évaluation
- TD3 CorrDocument4 pagesTD3 CorrImane KhaliPas encore d'évaluation
- Corrige Bac S Blanc 2015Document4 pagesCorrige Bac S Blanc 2015jad mamouPas encore d'évaluation
- Correction Ts Eval 8 15Document3 pagesCorrection Ts Eval 8 15annnnnnnnoussaPas encore d'évaluation
- Correction Examen S3 2021Document2 pagesCorrection Examen S3 2021Dona TeloPas encore d'évaluation
- L2 Psycho - 2019 - Trois Exercices Sur Ajustement de Proportion Et de MoyenneDocument3 pagesL2 Psycho - 2019 - Trois Exercices Sur Ajustement de Proportion Et de MoyenneZakaria chebriPas encore d'évaluation
- StatistiquesDocument5 pagesStatistiquesAbderrahmaneLamriPas encore d'évaluation
- 13 EchantillonageDocument5 pages13 Echantillonagelvtmath100% (1)
- Corrige Polynesie Spe j1 Sept 2022 FHDocument8 pagesCorrige Polynesie Spe j1 Sept 2022 FHkraby 92Pas encore d'évaluation
- Corrigé Épreuve Probabilités Session Ordinaire 2019 - SAID BENHMIDA PDFDocument2 pagesCorrigé Épreuve Probabilités Session Ordinaire 2019 - SAID BENHMIDA PDFElmehdi TalbiPas encore d'évaluation
- Annale Maths Bac S Centres Etrangers Juin 2019 CorrigeDocument13 pagesAnnale Maths Bac S Centres Etrangers Juin 2019 CorrigehessasPas encore d'évaluation
- Stat Inf Exos 2 CorDocument8 pagesStat Inf Exos 2 Corhayatoubouhouch01Pas encore d'évaluation
- TS DM5 CorrDocument6 pagesTS DM5 CorrKuengyPas encore d'évaluation
- Exo StatDocument4 pagesExo StatbattouiPas encore d'évaluation
- Proba Chap 5 ExoDocument7 pagesProba Chap 5 ExoBadr EddinePas encore d'évaluation
- dm06 Matrices de Bruijn Erdos CorrigeDocument7 pagesdm06 Matrices de Bruijn Erdos CorrigeTspeePas encore d'évaluation
- Chapitre 3 - Approximations Des Lois Et Convergenc S StochastiquesDocument32 pagesChapitre 3 - Approximations Des Lois Et Convergenc S StochastiquesChaymæ AdmirPas encore d'évaluation
- SuitesDocument10 pagesSuitesislamoud87Pas encore d'évaluation
- Resume Cours Suites TSDocument10 pagesResume Cours Suites TSSaliou DoumbiaPas encore d'évaluation
- Estimation Et Prévision Par IntervalleDocument23 pagesEstimation Et Prévision Par IntervalleBe-PositivePas encore d'évaluation
- Suites Numériques Limites (VP)Document8 pagesSuites Numériques Limites (VP)Calista PIRIS FERNANDESPas encore d'évaluation
- TS Chap 10: Cours Sur Les Lois de ProbabilitésDocument10 pagesTS Chap 10: Cours Sur Les Lois de Probabilitésexos2mathPas encore d'évaluation
- td1 Suites Cle031876Document5 pagestd1 Suites Cle031876Johnny KOZYKOJOKIANPas encore d'évaluation
- Chapitre 2 3Document11 pagesChapitre 2 3Lorenzo MPas encore d'évaluation
- Fic 00009Document9 pagesFic 00009Nézar TàHàPas encore d'évaluation
- DS1TS12012Document3 pagesDS1TS12012HarachinedPas encore d'évaluation
- Corrige Spe1 Amerique Nord 1 18 Mai 2022 RRDocument4 pagesCorrige Spe1 Amerique Nord 1 18 Mai 2022 RRmerag76668Pas encore d'évaluation
- TD ProbaDocument11 pagesTD ProbaMayssoun chaimaaPas encore d'évaluation
- Corriges c2Document7 pagesCorriges c2Kone DramanePas encore d'évaluation
- TD ANALYSE 1 Serie N° 1 S1 SMPC +corrigés 2013-2014 FSRDocument3 pagesTD ANALYSE 1 Serie N° 1 S1 SMPC +corrigés 2013-2014 FSRDrissi Naytt100% (1)
- Cours I, Chap 1Document7 pagesCours I, Chap 1Hélier de BailliencourtPas encore d'évaluation
- Corrige S Asie 20 Juin 2019Document9 pagesCorrige S Asie 20 Juin 2019SouleymanePas encore d'évaluation
- CorrectionPartielle Session1Examen20172018Document4 pagesCorrectionPartielle Session1Examen20172018RYDOUANE SIMBOROPas encore d'évaluation
- TH Eor' Eme Limite CentralDocument62 pagesTH Eor' Eme Limite CentralrokiahoumedsalehPas encore d'évaluation
- StudentDocument31 pagesStudentayoub.dergaoui90Pas encore d'évaluation
- DS MIMSE 2013 2014 CorrigeDocument4 pagesDS MIMSE 2013 2014 CorrigeSteves DoumanPas encore d'évaluation
- Théorème Central LimiteDocument64 pagesThéorème Central LimiteMedo ZnPas encore d'évaluation
- Fic 00009Document6 pagesFic 00009Aymen Ich Liebe MichPas encore d'évaluation
- TD1 - CorrigeDocument1 pageTD1 - CorrigethebestmathieuPas encore d'évaluation
- CCP - 2002 - MP - M1 - Corrige 2 PDFDocument4 pagesCCP - 2002 - MP - M1 - Corrige 2 PDFZouhair NajarPas encore d'évaluation
- Théoreme Moivre-LaplaceDocument39 pagesThéoreme Moivre-LaplaceAhmed AjebliPas encore d'évaluation
- Correction TD1Document4 pagesCorrection TD1Fatima ZahraPas encore d'évaluation
- Corrige - Ds Suites-LimiteDocument3 pagesCorrige - Ds Suites-Limitenaroel.26Pas encore d'évaluation
- Prob Et Stat InfDocument6 pagesProb Et Stat InfWalid Ben AliPas encore d'évaluation
- Correctionexam 1Document6 pagesCorrectionexam 1Babacar NdiayePas encore d'évaluation
- Corrige Pondichery S Avril 2014Document8 pagesCorrige Pondichery S Avril 2014Nestor GrahPas encore d'évaluation
- TP9 CorrigésDocument5 pagesTP9 CorrigésChristopher TruongPas encore d'évaluation
- Corrige Ds 1104Document10 pagesCorrige Ds 1104drohulrich51Pas encore d'évaluation
- Corrige STL Bio Antilles-Guyane Juin2016 FHDocument8 pagesCorrige STL Bio Antilles-Guyane Juin2016 FHToumany FofanaPas encore d'évaluation
- Maths Term Suites Ex CorrDocument12 pagesMaths Term Suites Ex Corrapi-203629011Pas encore d'évaluation
- Spe Mathematiques 2022 Metropole 1 CorrigeDocument10 pagesSpe Mathematiques 2022 Metropole 1 CorrigeLilaliloche SPas encore d'évaluation
- Suites Ages LDocument6 pagesSuites Ages LbilalastephenPas encore d'évaluation
- Corrige Polynesie Spe2 14 Mars 2023Document5 pagesCorrige Polynesie Spe2 14 Mars 2023lucie.devarrewaerePas encore d'évaluation
- Corrige Bac TS Liban 27 Mai 2015Document6 pagesCorrige Bac TS Liban 27 Mai 2015Céline LuttiPas encore d'évaluation
- - Tours de magie expliqués par des bienfaits du calcul littéralD'Everand- Tours de magie expliqués par des bienfaits du calcul littéralPas encore d'évaluation
- Dissertation Léopold Sedar SenghorDocument4 pagesDissertation Léopold Sedar SenghorLina Peña100% (4)
- Rapport Diagnostique LATIFA ETTAYEBDocument3 pagesRapport Diagnostique LATIFA ETTAYEBNAJEM FFPas encore d'évaluation
- Corrigé S1Document3 pagesCorrigé S1MohamedPas encore d'évaluation
- Bts SN 2023 E4 Metropole Sujet Documents Reponses Professionnel SnirDocument8 pagesBts SN 2023 E4 Metropole Sujet Documents Reponses Professionnel Snirz9qg8sjn62Pas encore d'évaluation
- Guide Cookielessconsentless 2021 01122021Document106 pagesGuide Cookielessconsentless 2021 01122021ericPas encore d'évaluation
- Java Notions Fondamentales Open ClassroomDocument223 pagesJava Notions Fondamentales Open ClassroomAnas SoryPas encore d'évaluation
- td2 Mes Inté 2023-2Document1 pagetd2 Mes Inté 2023-2Thinkpad LenovoPas encore d'évaluation
- Cheikh-Rabii-Faleh L'innocence Des Honnêtes Gens de Ce DontDocument20 pagesCheikh-Rabii-Faleh L'innocence Des Honnêtes Gens de Ce Dontasam93Pas encore d'évaluation
- Prise en Charge Des Vertiges en UrgenceDocument30 pagesPrise en Charge Des Vertiges en UrgenceAbdelmoumen DjazairiPas encore d'évaluation
- Chapitre 1 Mathématiques Groupe 4Document138 pagesChapitre 1 Mathématiques Groupe 4nadasamsunga03corePas encore d'évaluation
- BusinessDocument4 pagesBusinessdonasarahtPas encore d'évaluation
- Lecture Suivie ADocument1 pageLecture Suivie AnadiahettarPas encore d'évaluation
- Séquence 0Document34 pagesSéquence 0rihab Bouabid100% (1)
- CRPE Frs Sujet Zéro1Document5 pagesCRPE Frs Sujet Zéro1gaspar 70Pas encore d'évaluation
- Exercices Corriges Integrales GeneraliseesDocument13 pagesExercices Corriges Integrales Generaliseesjossef belkhierPas encore d'évaluation
- Mémoire-Master 2 Isil-ConvertiDocument75 pagesMémoire-Master 2 Isil-Convertiimene IBPas encore d'évaluation
- Expression Ecrite StrategiesDocument15 pagesExpression Ecrite StrategiesPapa NguiranePas encore d'évaluation
- L'étude de La RenaissanceDocument33 pagesL'étude de La RenaissanceE. R (Orion85)Pas encore d'évaluation
- InformatiqueDocument26 pagesInformatiqueimed imddPas encore d'évaluation
- Sapiro CVDocument30 pagesSapiro CVJeannePas encore d'évaluation
- Chapitre 1 OO - Classe-TransitionDocument41 pagesChapitre 1 OO - Classe-TransitionCho ChiPas encore d'évaluation
- TrigoReciproque 2020Document21 pagesTrigoReciproque 2020asflbleau footloisirPas encore d'évaluation
- Missel Romain Plaquette de PresentationDocument2 pagesMissel Romain Plaquette de PresentationmarthaenPas encore d'évaluation
- 1 Eso - Le Présent Du Verbe ÊtreDocument4 pages1 Eso - Le Présent Du Verbe ÊtrevaleriePas encore d'évaluation
- Sujets PFE: Rue de Lac Ghar El Melh Les Berges Du Lac 1053 TunisDocument16 pagesSujets PFE: Rue de Lac Ghar El Melh Les Berges Du Lac 1053 TunisFARAH BEN AMORPas encore d'évaluation