Polynmes de Tchebychev

Pafnouti Lvovitch Tchebychev, mathmaticien russe , est n Borovsk en 1821 et mort Saint-Ptersbourg en 1894.

1) Dnition et existence
a) Polynmes de Tchebychev de 1re espce : Tn . Soit n un entier naturel. Il existe un et un seul polynme not Tn tel que R, Tn (cos ) = cos(n). Unicit. Tn est dtermin sur [1, 1] qui est inni et donc uniquement dtermin. Existence. Soient n un entier naturel et un rel.
n

cos(n) = Re(ein ) = Re((cos + i sin )n ) = Re

k=0 E(n/2)

Ck (cos )nk (i sin )k n

E(n/2)

=
p=0 E(n/2)

(1)p C2p (cos )n2p (sin )2p = n

p=0

(1)p C2p (cos )n2p (1 cos2 )p n

et le polynme
p=0

(1)p C2p Xn2p (1 X2 )p convient. n

E(n/2)

n N, Tn =

(1)p C2p Xn2p (1 X2 )p . n

p=0

b) Polynmes de Tchebychev de 2me espce : Un . Soit n un entier naturel non nul. Il existe un et un seul polynme not Un tel que R, sin Un (cos ) = sin(n). Unicit. Un est dtermin sur ] 1, 1[ qui est inni et donc uniquement dtermin. Existence. Soient n un entier naturel et un rel.
n

sin(n) = Im(ein ) = Im((cos + i sin )n ) = Im

k=0 E((n1)/2)

Ck (cos )nk (i sin )k n

E((n1)/2) 2p+1 (1)p Cn (cos )n2p1 (1 cos2 )p p=0

=
p=0

2p+1 (1)p Cn (cos )n(2p+1) (sin )2p+1 = sin

E((n1)/2)

et le polynme
p=0

2p+1 (1)p Cn Xn2p1 (1 X2 )p convient.

E((n1)/2)

n N , Un =

2p+1 (1)p Cn Xn2p1 (1 X2 )p . p=0

2) Relation entre Tn et Un
Soit n un entier naturel non nul. Pour tout rel , on a Tn (cos ) = cos(n). En drivant cette relation, pour tout rel on obtient
sin Tn (cos ) = n sin(n),

http ://www.maths-france.fr

c Jean-Louis Rouget, 2007. Tous droits rservs.

ou encore R, sin Par unicit de Un , on a donc n N , Un = 1 T . n n 1 Tn n

(cos ) = sin(n).

3) Relation de rcurrence
Pour tout rel et tout entier naturel n, on a cos(n) + cos((n + 2)) = 2 cos cos((n + 1)), ce qui fournit encore R, Tn (cos ) + Tn+2 (cos ) = 2 cos Tn+1 (cos ). ou enn x [1, 1], Tn (x) + Tn+2 (x) = 2xTn+1 (x). Ainsi, les polynmes Tn + Tn+2 et 2XTn+1 concident en une innit de valeurs et sont donc gaux. n N, Tn+2 2XTn+1 + Tn = 0.

4) Premires expressions de Tn et Un
A partir de la relation de rcurrence ou partir de lexpression de Tn du 1)a) ou encore en calculant directement cos(2), cos(3), . . . , on obtient : T0 = 1, T1 = X, T2 = 2X2 1, T3 = 4X3 3X, T4 = 8X4 8X2 + 1 et T5 = 16X5 20X3 + 5X. De mme, partir de lgalit Un = 1 T , on obtient n n

U1 = 1, U2 = 2X, U3 = 4X2 1, U4 = 8X3 6X et U5 = 16X4 12X2 + 1.

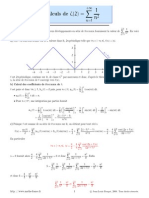
5) Graphes des premiers Tn

1 T0

T1

http ://www.maths-france.fr

T2

c Jean-Louis Rouget, 2007. Tous droits rservs.

T3

6) Degr, coecient dominant

1 re solution. Soit n N . On rappelle que
E(n/2)

Tn =
p=0

(1)p C2p Xn2p (1 X2 )p . n

n Puisque pour tout entier naturel p 0, E( ) , on a n 2p + 2p = n, Tn est un polynme de degr infrieur ou gal n. 2 De plus, le coecient de Xn dans Tn vaut C0 + C2 + C4 + . . . = n n n 1 1 ((C0 + C1 + C2 + C3 + . . .) + (C0 C1 + C2 C3 + . . .)) = ((1 + 1)n + (1 1)n ) n n n n n n n n 2 2 1 n = (2 + 0) ((1 1)n = 0 car n 1) 2 = 2n1 .

2 me solution. Montrons par rcurrence que n N , deg(Tn ) = n et dom(Tn ) = 2n1 . On a dj deg(T1 ) = 1, deg(T2 ) = 2, dom(T1 ) = 1 = 211 et dom(T2 ) = 2 = 221 . Le rsultat est donc vrai pour n = 1 et n = 2. Soit n 1. Supposons que deg(Tn ) = n, deg(Tn+1 ) = n + 1, dom(Tn ) = 2n1 et dom(Tn+1 ) = 2n alors deg(Tn+2 ) = deg(2XTn+1 Tn ) = deg(XTn+1 ) = 1 + n + 1 = n + 2, et dom(Tn+2 ) = dom(2XTn+1 ) = 2 2n = 2n+1 . Le rsultat est dmontr par rcurrence. T0 = 1 et n N , deg(Tn ) = n et n N , dom(Tn ) = 2n1 . Par drivation , on obtient n N , deg(Un ) = n 1 et n N , dom(Un ) = 2n1 .

7) Parit
Pour tout naturel n, Tn a la parit de n. En eet,
E(n/2) E(n/2)

Tn (X) =
p=0

(1)p C2p (X)n2p (1 (X)2 )p = (1)n n

p=0

(1)p C2p Xn2p (1 X2 )p = (1)n Tn . n

On peut aussi crire pour tout rel : Tn ( cos ) = Tn (cos( + )) = cos(n + n) = (1)n cos(n) = (1)n Tn (cos), et donc, pour tout rel x de [1, 1], Tn (x) = (1)n Tn (x). Puisque [1, 1] est inni, les polynmes Tn (X) et (1)n Tn sont gaux. On peut encore utiliser la relation de rcurrence du 3). Tout dabord, T0 (X) = (1)0 T0 et T1 (X) = (1)1 T1 . Ensuite, si pour n 0 Tn (X) = (1)n Tn et Tn+1 (X) = (1)n+1 Tn+1 alors Tn+2 (X) = 2(X)Tn+1 (X) Tn (X) = 2(1)n+2 XTn+1 (1)n Tn = (1)n+2 (2XTn+1 Tn ) = (1)n+2 Tn+2 . Pour tout naturel n, Tn a la parit de n. Par drivation , on obtient encore : pour tout naturel non nul n, Un a la parit contraire de n.

http ://www.maths-france.fr

c Jean-Louis Rouget, 2007. Tous droits rservs.

8) Tn(1), Tn(1), Tn(0) (=coecient constant)

Soit n N. Tn (1) = Tn (cos 0) = cos(n 0) = 1. Tn (1) = (1)n Tn (1) = (1)n . T2n+1 est impair et donc T2n+1 (0) = 0. Puis T2n (0) = T2n (cos ) = cos(n) = (1)n . 2 En rsum n N, Tn (1) = 1, n N, Tn (1) = (1)n , n N, T2n+1 (0) = 0 et T2n (0) = (1)n ou encore Tn (0) = cos(n ). 2

9) Equation direntielle vrie par Tn. Coecients de Tn

a) Equation direntielle vrie par Tn . Pour trouver les coecients de Tn , on cherche dabord une quation direntielle linaire dont Tn est solution. Soit n N. En drivant lgalit Tn (cos ) = cos(n), on obtient :
R, sin Tn (cos ) = n sin(n),

puis en redrivant
R, cos Tn (cos) + sin2 Tn (cos ) = n2 cos(n) = n2 Tn (cos),

ou encore,
x [1, 1], xTn (x) + (1 x2 )Tn (x) = n2 Tn (x).

Ainsi, puisque [1, 1] est inni,

n N, (1 X2 )Tn XTn + n2 Tn = 0 (E).

b) Coecients de Tn . Soit n 2. Puisque Tn est de degr n et a la parit de n, on peut poser Tn =

0k n 2

ak Xn2k .

Reportons alors cette criture de Tn , dans le premier membre de lquation (E).

(1 X2 )Tn XTn + n2 Tn = (1 X2 )

(n 2k)(n 2k 1)ak Xn2k2 X

0k n 1 2 0k n1 2

(n 2k)ak Xn2k1

+ n2
0k n 2

ak Xn2k (n 2k)(n 2k 1)ak Xn2k2 (n 2k)(n 2k 1)ak Xn2k

0k n 2

=
0k n 2

0k n 1 2

(n 2k)ak Xn2k + n2
0k n 2

ak Xn2k

= +
0k n 2

(n 2(k + 1) + 2)(n 2(k + 1) + 1)ak Xn2(k+1)

0k n 1 2

((n 2k)(n 2k 1) (n 2k) + n2 )ak Xn2k (n 2k + 2)(n 2k + 1)ak1 Xn2k +

1k n 2 0k n 2

= =
1k n 2

(4kn 4k2 )ak Xn2k

[(n 2k + 2)(n 2k + 1)ak1 + 4k(n k)ak ]Xn2k .

Par suite, http ://www.maths-france.fr 4

c Jean-Louis Rouget, 2007. Tous droits rservs.

En tenant compte de a0 = dom(Tn ) = 2n1 ak =

(1 X2 )Tn XTn + n2 Tn = 0 k N, (1 k

n (n 2k + 2)(n 2k + 1)ak1 + 4k(n k)ak = 0). 2 n , pour 1 k , on a alors 2

(n 2k + 1)(n 2k + 2) (n 2k + 3)(n 2k + 4) (n 1)n ... a0 4k(n k) 4(k 1)(n k + 1) 4 1 (n 1) (1)k (n 2k + 1) (n 2k + 2) (n 2k + 3) (n 2k + 4) . . . (n 1) n n1 2 = 4k k (k 1) . . . 2 1 (n 1) (n 2) . . . (n k) (n k)! n n!/(n 2k)! = (1)k 2n2k1 = (1)k 2n2k1 k! (n 1)!/(n k 1)! n k k!(n 2k)! n Ck . = (1)k 2n2k1 n k nk n Ck Xn2k . n k nk

ce qui reste vrai pour k = 0. n N , Tn = (1)k 2n2k1

0k n 2

10) Racines de Tn et factorisation de Tn

Soient R et n N . cos(n) = 0 n + Z + Z. 2 2n n

Pour k 0, n 1 , posons alors k =

k + puis xk = cos k . On a dune part 2n n 0< = 0 < 1 < . . . < n1 = < , 2n 2n

et donc, par stricte dcroissance de la fonction x cos x sur [0, ],

1 > x0 > x1 > . . . > xn1 > 1.

En particulier, les n nombres xk , 0 k n 1, sont deux deux distincts. Mais dautre part, pour k 0, n 1 , Tn (cos k ) = cos(nk ) = 0. et les n nombres xk , 0 k n 1 sont n racines deux deux distinctes du polynme Tn qui est de de degr n. Ce sont donc toutes les racines de Tn , toutes relles simples et dans ] 1, 1[. En tenant compte de dom(Tn ) = 2n1 , on a montr que 1) n N , Tn a n racines relles deux deux distinctes, toutes dans ] 1, 1[.
n1

2) n N , Tn = 2n1

X cos
k=0

k + 2n n

11) Diverses expressions de Tn et Un

a) Pour x dans [1, 1]. Soit n N. Soient x [1, 1] puis = Arccos x. On a alors [0, ] et cos = x. Lgalit Tn (cos) = cos(n) scrit encore : n N, x [1, 1], Tn (x) = cos(n Arccos x). De mme, lgalit sin Un (cos ) = sin(n) scrit encore : n N, x ] 1, 1[, Un (x) = sin(n Arccos x) . 1 x2

b) Pour |x| 1. Montrons par rcurrence que, pour tout entier naturel n et tout rel , on a Tn (ch ) = ch(n). Cest clair pour n = 0 et n = 1. Soit n 0. Supposons que Tn (ch ) = ch(n) et que Tn+1 (ch ) = ch((n + 1)). On en dduit que Tn+2 (ch ) = 2(ch )Tn+1 (ch ) Tn (ch) = 2(ch )(ch(n + 1)) ch(n) = ch((n + 2)) ch(n) + ch(n) = ch((n + 2)). http ://www.maths-france.fr 5
c Jean-Louis Rouget, 2007. Tous droits rservs.

On a montr par rcurrence que n N, R, Tn (ch ) = ch(n).

En drivant, on obtient sh Tn (ch ) = n sh(n) et, en tenant compte de Tn = nUn , on obtient

n N , R, (sh )Un (ch ) = sh(n). Soient alors x un rel suprieur ou gal 1 puis = argch x = ln(x + x2 1). Tn (x) = Tn (ch ) = ch(n) 1 n ln(x+x2 1) 1 2 e (x + = + en ln(x+ x 1) = 2 2 1 = (x + x2 1)n + (x x2 1)n (car (x + 2 x [1, +[, Tn (x) =

x2 1)n + (x + x2 1)(x

x2 1)n

x2 1) = 1).

1 (x + x2 1)n + (x x2 1)n . 2

Par parit, on peut obtenir les valeurs de Tn pour x 1. En drivant, on obtient pour x > 1 : x 1 1 x 1 T (x) = n (1 + )(x + x2 1)n1 + (1 )(x n n 2 n x2 1 x2 1 1 = (x + x2 1)n (x x2 1)n . 2 x2 1 1 n N , x ]1, +[, Un (x) = (x + x2 1)n (x x2 1)n . 2 x2 1 c) Pour z complexe non nul. Lgalit Tn (cos ) = cos(n), valable pour tout rel , scrit encore Tn 1 i (e + ei ) 2 = 1 in (e + ein ), 2

Un (x) =

x2 1)n1

ou encore, pour tout nombre complexe z de module 1, Tn Par suite, les polynmes Xn Tn en dduit que z C , Tn 1 1 (z + ) 2 z = 1 n 1 (z + n ). 2 z 1 n 1 (X + n ) 2 X 1 1 (z + ) 2 z et = 1 2 zn + 1 . zn

1 2n (X + 1) concident en une innit de valeurs et sont donc gaux. On 2

12) Extrema de Tn et Un sur [1, 1]

a) Extrema de Tn Daprs 11)a), pour tout rel et tout entier naturel n, Tn (ch ) = ch(n). Ceci montre que pour x rel lment de ]1, +[ et n entier naturel non nul, on a Tn (x) > 1. Par parit de Tn , on a donc x R, n N , (|x| > 1 |Tn (x)| > 1).

Mais puisque pour tout R et tout entier naturel non nul n Tn (cos ) = cos(n), on a aussi x R, n N , (|x| 1 |Tn (x)| 1).

http ://www.maths-france.fr

c Jean-Louis Rouget, 2007. Tous droits rservs.

Soient alors x un rel de [1, 1] et = Arccos x. |Tn (x)| = 1 | cos(n)| = 1 n Z k k Z k Z/ x cos k 0, n / x cos . n n n

Lquation |Tn (x)| = 1 admet, dans R, exactement n + 1 solutions, toutes dans [1, 1], savoir k les n + 1 rels xk = cos , k 0, n . n

On en dduit encore n N, b) Extrema de Un Tout dabord on note que n N , R, | sin(n)| n| sin |. Montrons le rsultat par rcurrence. Soit R. Cest clair pour n = 1. Soit n 1. Si | sin(n)| n| sin | alors | sin((n + 1))| = | sin(n) cos + cos(n) sin | | sin(n)| | cos | + | cos(n)| | sin | | sin(n)| + | sin | n| sin | + | sin | = (n + 1)| sin |, ce qui dmontre par rcurrence lingalit propose. Par suite, pour n entier naturel non nul et non dans Z, |Un (cos )| = valable pour x = 1 ou x = 1 par continuit) : n N , x [1, 1], |Un (x)| n. Soit n 2. En reprenant le raisonnement par rcurrence ci-dessus, si on a | sin(n)| = n| sin | alors toutes les ingalits crites sont des galits et on a ncessairement | sin(n)| = | sin((n 1))| | cos | + | cos((n 1))| | sin | = | sin((n 1))| + | sin | = n| sin |. Ceci impose | sin((n 1))| = 0 car si | sin((n 1))| = 0 alors Z, puis | cos | < 1 et on na pas lgalit. En rsum, / si Z, Un (cos )| = / sin(n) < n. sin sin(n) , on obtient |Un (1)| = |Un (1)| = n. sin sin(n) n ou encore (lingalit restant sin
x[1,1]

Max |Tn (x)| = 1.

Maintenant, quand tend vers 0 ou vers dans lgalit Un (cos )| = Finalement n N,

x[1,1]

Max |Un (x)| = n.

Pour n 2, lquation |Un (x)| = n admet dans [1, 1] exactement deux solutions savoir 1 et 1.

13)

forme de la fonction nulle sur [1, 1].

Soit n N . Soit tn = Tn 2n1 1 et P un polynme unitaire de degr n 1. Il sagit de montrer que ||tn|| = o ||P|| = Max |P(x)|.
x[1,1]

Tn 2n1

est le polynme unitaire de degr n ralisant la meilleure approximation uni-

1 2n1

||P|| .

Supposons par labsurde que ||P|| <

1 = ||tn || . 2n1 7
c Jean-Louis Rouget, 2007. Tous droits rservs.

http ://www.maths-france.fr

Considrons les nombres xk = cos tn (x2 ) = 1 2n1 > P(x2 ). . .

k 1 1 , 0 k n. Alors tn (x0 ) = n1 > P(x0 ) puis tn (x1 ) = n1 < P(x1 ) puis n 2 2

Ainsi, le polynme tn P change de signe dans chacun des n intervalles ]xk , xk+1 [, 0 k n 1 et admet donc au moins n racines deux deux distinctes. Mais ce polynme est de degr infrieur ou gal n 1 car P et tn sont unitaires de degr n. Donc tn P est nul cce qui contredit ||P|| < ||tn || . Finalement, pour tout polynme P unitaire de degr n 1, ||P|| 1 1 = n1 Tn . 2n1 2

1 Montrons de plus que tn est lunique polynme unitaire P de degr n vriant ||P|| = n1 . 2 1 Soit donc P un polynme unitaire de degr n tel que ||P|| = n1 puis Q = tn P. Soit LQ le polynme dinterpolation 2 k , 0 k n. On rappelle que de Lagrange de Q en les n + 1 rels xk = cos n
n

LQ =
k=0

k
j=k

(X xi ) o k =

Q(xk ) (xk xj )
j=k

Par hypothse, x [1, 1],

1 2n1

P(x)

1 2n1

et comme tn (xk ) =

(1)k , on en dduit que 2n1

k 0, n , (1)k Q(xk ) 0. Dautre part, (1)k

j=k

(xk xj ) 0 et donc k 0, n , k 0.

Maintenant, Q et LQ sont deux polynmes de degr au plus n qui concident en les (n + 1) rels deux deux distincts xk , 0 k n. On a donc LQ = Q et en particulier, deg(LQ ) = deg(Q) n 1. Le coecient de Xn dans LQ est donc nul. Ceci fournit
n

k = 0.
k=0

Finalement, les k sont des rels positifs de somme nulle et ils sont donc tous nuls. On en dduit que Q = 0 et donc P = tn . pour tout polynme P, unitaire de degr n 1, ||P|| avec galit si et seulement si P = 1 1 = n1 Tn 2n1 2

1 Tn . 2n1

14) Srie entire associe Tn et Un

Soit z = rei , r R+ , R un nombre complexe tel que |r| < 1. + 1 Le dveloppement = zn valable quand |z| < 1 fournit 1z
n=0 +

rn ein =
n=0

1 rei 1 r cos + ir sin 1 = , = i i )(1 rei ) 1 re (1 re 1 2r cos + r2

et par identication des parties relles et imaginaires, on obtient :

+

r ] 1, 1[, R, , ce qui scrit encore http ://www.maths-france.fr

rn cos(n) =
n=0

1 r cos et 1 2r cos + r2 8

rn sin(n) =
n=0

r sin . 1 2r cos + r2

c Jean-Louis Rouget, 2007. Tous droits rservs.

r ] 1, 1[, R, , ou enn

n=0

1 r cos r Tn (cos ) = et sin 1 2r cos + r2

n

rn Un (sin ) =
n=0

r sin , 1 2r cos + r2

t ] 1, 1[, x [1, 1], ,

tn Tn (x) =
n=0

1 t cos et 1 2t cos + t2

tn Un (x) =
n=0 +

t . 1 2t cos + t2 t ). 1 2tx + t2

(Pour t x dans ] 1, 1[ et x {1, 1}, le plus simple est de vrier directement On obtient aussi
+

tn Un (x) =
n=0

1+2
n=0

tn Tn (x) = 2

1 t2 1 tx 1 +1= . 1 2tx + t2 1 2tx + t2

On peut procder autrement. Un calcul formel fournit

+ + + +

2xt
n=1

Tn (x)tn = = t2

(Tn1 (x) + Tn+1 (x))tn+1 = t2

n=1 + + n=1

Tn1 (x)tn1 +
n=1

Tn+1 (x)tn+1

1+
n=1

Tn (x)tn

+
n=1

Tn (x)tn xt,

puis
+ +

(t2 2xt + 1)
n=1

Tn (x)tn = xt t2 et donc (t2 2xt + 1) 1 + 2

n=1

Tn (x)tn

= 1 t2 .

Rciproquement, x rel x, la fraction rationnelle en srie entire. Si on pose, pour x rel x, 1 t2 = 1 2tx + t2
+

1 t2 nadmet donc pas zro pour ple et est donc dveloppable 1 2tx + t2
+

an (x)tn pour t dans ] R, R[,

n=0

lgalit (t2 2xt + 1)

n=0

an (x)tn = 1 t2 valable pour t ] R, R[ fournit

+ + +

an (x)tn 2x
n=0 n=1

an1 (x)tn +
n=2

an2 (x)tn = 1 t2 .

Par suite, a0 (x) = 1, a1 (x) = 2x = 2T1 (x), a2 (x) = 4x2 2 = 2T2 (x) et pour n 3, an (x) 2xan1 (x) + an2 (x) = 0. Par rcurrence, il est alors clair que pour tout rel x, a0 (x) = 1 et que n 1, an (x) = 2Tn (x). Maintenant, si |x| 1, les ples de la fraction rationnelle sont de module 1 et on sait que le rayon de convergence de la srie est 1. Si x > 1, les ples sont x x2 1 et x + x2 1 avec 0 < x x2 1 < x + x2 1 et dans ce cas, le rayon, qui est le minimum des modules des ples, est R = x x2 1. Si x < 1, les ples sont encore x x2 1 et x + x2 1 avec x x2 1 < x + x2 1 < 0 et dans ce cas, le rayon est R = x x2 1. En rsum, si |x| > 1, la srie a un rayon de convergence gal |x| x2 1.

http ://www.maths-france.fr

c Jean-Louis Rouget, 2007. Tous droits rservs.

15) Orthogonalit des polynmes Tn

a) Un produit scalaire sur R[X]. Soit : R[X] R[X] R . Montrons que est un produit scalaire sur R[X]. 2 1 P(t)Q(t) (P, Q) dt 1 1 t2

P(t)Q(t) est continue sur ] 1, 1[ et donc localement Tout dabord, si P et Q sont deux polynmes, la fonction t 1 t2 P(t)Q(t) 1 P(t)Q(t) intgrable sur ] 1, 1[. De plus, quand t tend vers 1, = O = et quand t tend vers 1, 1t 1 t2 1 t2 P(t)Q(t) 1 est intgrable sur ] 1, 1[. (que 1 ou 1 soient ou non racines de P ou Q) et donc la fonction t O 1+t 1 t2 Ainsi, pour tous polynmes P et Q, (P, Q) existe dans R. La bilinarit , la symtrie et la positivit de sont claires. Soit enn P R[X]. (P, P) = 0 P2 (t) dt = 0 1 t2 1 t ] 1, 1[, P2 (t) = 0 (fonction continue, positive, dintgrale nulle sur ] 1, 1[) P = 0 (polynme ayant une innit de racines). R[X] R[X] (P, Q) b) Orthogonalit des polynmes Tn . 2
1 1 1

R est un produit scalaire sur R[X]. P(t)Q(t) dt 1 t2

car sin 0 pour [0, ]. On obtient Tn |Tm = 2

1 1 0

Soient n et m deux entiers naturels. En posant t = cos pour [0, ], on a dt = sin d ou encore d =

1 dt 1 t2

Tn (t)Tm (t) dt 1 t2

2 = 2 =

Tn (cos )Tm (cos ) (d) cos(n) cos(m) d =

0

(cos((n + m)) + cos((n m))) d

0

Ainsi, si n = m, (Tn , Tm ) = 0, si n = m = 0, (Tn , Tm ) = 1 si n = m = 0, (Tn , Tm ) = 2. Finalement, puisque dautre part n N, deg(Tn ) = n, on a montr que : T0 ( ) (Tn )nN est une base orthonorme de lespace prhilbertien (R[X], |) o 2 2 1 P(t)Q(t) (P, Q) (R[X])2 , P|Q = dt. 1 1 t2

16) Intervention des polynmes de Tchebychev dans linterpolation de Lagrange

Cest lun des intrts principaux des polynmes de Tchebychev. Rappelons une expression de lerreur commise dans linterpolation de Lagrange. Si f est une fonction de classe Cn+1 sur [a, b], si x0 < . . . < xn sont n + 1 rels deux deux distincts de [a, b] et si Lf est le polynme dinterpolation de Lagrange en x0 ,. . . , xn alors, pour tout rel x de [a, b], il existe un rel c dans ]a, b[ tel que f(x) Lf (x) = N(x) http ://www.maths-france.fr f(n+1) (c) o N(x) = (n + 1)! 10
n

(x xk ),
k=0

c Jean-Louis Rouget, 2007. Tous droits rservs.

et en particulier sup |f(x) Lf (x)| sup |N(x)| sup

x[a,b]

x[a,b]

|f(n+1) (c)| . t[a,b] (n + 1)!

On se place sur [a, b] = [1, 1]. Pour minimiser lerreur commise dans linterpolation de Lagrange, il sagit de choisir N de sorte que sup |N(x)| soit le plus petit possible. N est un polynme unitaire de degr n + 1 et le 13) montre que
x[a,b]

sup |N(x)| est minimum pour N =

x[1,1]

1 Tn+1 . 2n

http ://www.maths-france.fr

11

c Jean-Louis Rouget, 2007. Tous droits rservs.