Af 141

Dossier délivré pour
DOCUMENTATION
19/09/2008
Séries de Fourier
par Hervé QUEFFÉLEC

Professeur de mathématiques à l’Université de Lille
1. Coefficients de Fourier d’une fonction 2π – périodique ................ AF 141 - 3

1.1 Classes de fonctions localement intégrables............................................. — 3
1.2 Formules de Fourier ..................................................................................... — 3
1.3 Convolution de deux fonctions et théorème d’unicité .............................. — 4
1.4 Cas des séries uniformément convergentes.............................................. — 5
1.5 Règles de calcul ............................................................................................ — 6
2. Développement en série de Fourier..................................................... — 6
2.1 Noyau de Dirichlet........................................................................................ — 6
2.2 Théorème de Dirichlet.................................................................................. — 7
2.3 Principe de localisation de Riemann et retour à Dirichlet......................... — 8
3. Exemples de développement en série de Fourier ............................ — 9
3.1 Cas des fonctions paires ou impaires......................................................... — 9
3.2 Fonction signal. Fonction triangle............................................................... — 10
3.3 Fonction |cos|. Théorème de Weierstrass .................................................. — 10
4. Cas des fonctions localement de carré intégrable ......................... — 11
4.1 Base des exponentielles imaginaires ......................................................... — 11
4.2 Inégalité de Bessel. Identité de Parseval .................................................... — 12
4.3 Fonctions de classe C 1 et convergence normale. ..................................... — 13
4.4 Retour au théorème de Weierstrass ........................................................... — 13
5. Équation de la chaleur pour une barre finie...................................... — 13
5.1 Modélisation du problème .......................................................................... — 13
5.2 Séparation des variables et séries de Fourier............................................ — 14
5.3 Principe du maximum.................................................................................. — 14
5.4 Théorème d’existence et d’unicité .............................................................. — 15
6. Applications diverses des séries de Fourier ..................................... — 16
6.1 Inégalité de Wirtinger................................................................................... — 16
6.2 Une équation aux différences ..................................................................... — 17
6.3 Critère de Weyl. Loi de Benford .................................................................. — 18
Références bibliographiques .......................................................................... — 20
appelons qu’une fonction f : R → C est dite T – périodique si,

R f (x + T ) = f (x )
pour tout x réel ;
On peut toujours se ramener à T = 2 π, quitte à considérer g(x) = f  ------- .
Tx
2π
Une des propriétés essentielles du nombre π est que les fonctions cos nx,
sin nx, einx (où n est entier), appelées « signaux élémentaires », sont 2 π - pério-
diques ainsi que leurs combinaisons linéaires ; une question naturelle se pose
alors : obtient-on ainsi toutes les fonctions 2 π – périodiques ? On va voir que la
réponse est essentiellement « oui » si on autorise les combinaisons linéaires
infinies (séries), mais des problèmes délicats de régularité de la fonction f et de
convergence des séries surgissent.
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
© Techniques de l’Ingénieur, traité Sciences fondamentales AF 141 − 1

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
SÉRIES DE FOURIER ____________________________________________________________________________________________________________________
La théorie des séries de Fourier, initiée par Fourier dans sa Théorie analyti-
que de la chaleur, avait au départ un but analogue : montrer que toutes les solu-
tions d’une certaine équation aux dérivées partielles, dite équation de la chaleur
(nous l’étudierons dans les applications), s’obtiennent comme superposition de
solutions élémentaires ; cette théorie a aujourd’hui pour but de préciser
comment une fonction f 2 π – périodique plus ou moins arbitraire peut s’obtenir
à partir des signaux élémentaires et réciproquement de voir les fonctions f qu’on
obtient en prenant des combinaisons linéaires infinies plus ou moins arbitraires
∑ cn e
i nx
des signaux élémentaires, disons :
— la première opération s’appelle l’analyse de f ;

— la seconde la synthèse des signaux cn einx.
Ces deux opérations sont inverses l’une de l’autre, comme la dérivation et

l’intégration.
Considérons l’exemple du noyau de Poisson Pr , donné par la formule :
2
1–r
P r ( t ) = --------------------------------------- (0 < r < 1). (A)
2
1 – 2 r cos t + r
L’analyse de Pr , 2 π – périodique, conduit à montrer qu’il se représente par la

série normalement convergente :
∞
∑r
n i nt
e . (B)
–∞
n
Inversement, la synthèse des signaux r eint conduit à :
∞ ∞ ∞
∑r e ∑r e + ∑r e
n i nt n i nt n – i nt
= – 1 = (1 – r eit )–1 + (1 – r e–it )–1 – 1
–∞ 0 0
2
1–r
= ---------------------------------------2 ,
1 – 2 r cos t + r
et on retrouve la relation (A).
On dispose alors pour Pr de deux avatars (c’est l’un des grands intérêts de la
théorie, limité par le principe d’incertitude d’Heisenberg) :
— l’avatar « fonction » (A), sur lequel on lit par exemple la positivité de Pr , peu
claire sous la forme (B) ;
— l’avatar « série de Fourier » (B), sur lequel on lit par exemple que :
1
------
2π
E
0
2π
P r ( t )d t = 1 ,
ce qui est peu clair sous la forme (A).
De façon générale, comment fait-on pour associer à une fonction f une série de
∞
∑ cn e
i nx
Fourier , c’est-à-dire comment fait-on pour calculer les cn en fonction
–∞
de f ? C’est ce que nous allons voir dans la suite.
AF 141 − 2 © Techniques de l’Ingénieur, traité Sciences fondamentales

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
____________________________________________________________________________________________________________________ SÉRIES DE FOURIER
Il sera commode d’introduire également l’espace C k (k > 0) des

1. Coefficients de Fourier fonctions 2π – périodiques k fois continûment dérivables et de
d’une fonction poser :
2π – périodique ||f ||∞ = sup {|f (t )| ; t ∈R} pour f ∈ C 0
E
2π
1
||f ||1 = ------- f(t) dt pour f ∈ L 1.
2π 0
1.1 Classes de fonctions localement
intégrables
1.2 Formules de Fourier
Nous aurons besoin des relations d’orthogonalité simples sui-
vantes, où δp, q désigne le symbole de Kronecker :
Soit f ∈ L 1 ; motivés par le cas particulier précédent, définissons
E les coefficients de Fourier an (f ), bn (f ), cn (f ) par les formules :

2π
i(p – q)t dt
e ------- = δ p , q (p, q ∈ Z ) (3)
E
0 2π 2π
1
a n ( f ) = --- f ( t ) cos n t d t (n ∈ N) (6)
π
E E
2π 2π 0
dt dt 1
cos p t cos qt ------- = sin p t sin q t ------- = --- δ p, q (p, q ∈ N*) (4)
E
0 2π 2π 2 2π
0 1
b n ( f ) = --- f ( t ) sin n t d t ( n ∈ N* ) (7)
π
E
2π 0
dt
sin p t cos q t ------- = 0 (p, q ∈ N). (5)
E
2π 2π
0 1 – i nt
c n ( f ) = ------- f ( t )e dt (n ∈ Z) (8)
Considérons une combinaison linéaire finie f de signaux 2π 0
élémentaires :
On pose aussi fˆ (n ) = cn (f ) et fˆ : Z → C s’appelle la transformée
N N
a de Fourier de la fonction f.
∑ ck e = -----0- + ∑ ( a k cos k t + b k sin k t ) .
i kt
f(t) =
2 La proposition suivante rassemble quelques règles de calcul
–N 1
utiles.
Si |n | < N , on voit à l’aide de (3) que :
Proposition 1
E E
2π N 2π N
– i nt d t i(k – n)t dt
f ( t )e ------- =
2π ∑ ck 0
e ------- =
2π ∑ c k δ k, n = c n , Soit f ∈ L 1, a ∈ R, n ∈ N* ; alors :
E E E E
0
–N –N 2π a + 2π 2π 2π
et de même : a) f ( t )d t = f ( t )d t = f ( t + a )d t = f ( – t )d t
0 a 0 0
Eft
π
1 a an – i bn an + i bn
a n = --- ( ) cos nt d t (0 < n < N) , b) c 0 = -----0- ; c n = -------------------- ; c –n = --------------------
π 0 2 2
-
2
-
Eft
π c) a0 = 2c0 ; an = cn + c–n ; bn = i(cn – c–n )
1
b n = --- ( ) sin n t d t (1 < n < N) .
π 0 On a posé : an = an (f ), bn = bn (f ), cn = cn (f ).
■ On peut donc reconstituer les coefficients an , bn , cn à l’aide Preuve. ◊ Il s’agit de vérifications faciles ; par exemple, utilisant
d’intégrales portant sur f ; ici, f est continue et les intégrales en ques- la 2π–périodicité de f, on a :
tion sont des intégrales de Riemann de fonctions continues sur le
E Eft E E
a + 2π 0 2π 2π + a
segment [0, 2π] : leur existence ne pose donc pas de problème. Il
n’en est plus de même pour une fonction f quelconque. C’est pour- f ( t )d t = ( )d t + f ( t )d t + f ( t )d t
a a 0 2π
quoi nous allons restreindre notre étude aux deux classes
E E E
suivantes : 0 2π a
— la classe 5 des fonctions 2π – périodiques Riemann – = ... + ... + ...

a 0 0
intégrables sur tout segment [a, b] de R ;
E
2π
— la classe L 1 des fonctions 2π – périodiques Lebesgue –
intégrables sur tout segment [a, b] de R (on dit aussi localement = f ( t )d t . ◊
0
intégrables), avec l’abus de langage habituel qui consiste à identi-
fier deux fonctions f et g de L 1 égales presque partout (en toute Pour N entier > 0, la quantité :
rigueur, il faudrait parler de classes d’équivalence de fonctions,
N N
nous nous en abstiendrons ici). a
∑ cn e = -----0- + ∑ ( a n cos n x + b n sin n x )
i nx
SN ( f , x ) =
Si f ∈ 5 , on manipulera des intégrales de Riemann ; si f ∈ L 1, on 2
–N 1
manipulera des intégrales de Lebesgue.
Le lecteur réfractaire à ces dernières peut tout penser, sans grand s’appelle la valeur en x de la somme partielle d’indice N de f ; la
dommage, en termes d’intégrales de Riemann ; mais l’un des inté- fonction x ° SN (f, x ) est la somme partielle d’indice N de f.
rêts du point de vue de Lebesgue est de manipuler des espaces Pour n ∈ Z , en est la fonction x ° einx, et on a donc :
fonctionnels complets, et d’obtenir des énoncés très précis en
réponse aux questions de l’introduction : par exemple le fait que les N
eint (n ∈ Z) forment une base hilbertienne de l’espace L 2 (cf. § 4, SN (f ) = ∑ cn (f ) en .
théorème 11). –N

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
1.3 Convolution de deux fonctions

et théorème d’unicité a) L’homomorphisme f ° fˆ n’est pas surjectif.
b) On a cependant le résultat suivant, qui indique qu’on n’a
L 1 muni de la norme || ||1 est ce qu’on appelle un espace de rien de mieux pour la suite fˆ que d’être de limite nulle (contrai-
Banach, c’est-à-dire un espace vectoriel normé complet ; mais le
produit usuel fg de deux fonctions f, g ∈ L 1 n’est pas en général rement à ce qui se passera pour f ∈ L 2) : si (εn ) ∈ c0 , on peut
dans L 1. trouver f ∈ L 1 telle que :
Il existe cependant sur L 1 un autre produit, appelé produit de
convolution, et noté *, qui rend les plus grands services : | fˆ (n )| > |εn | pour tout n ∈ Z
E et telle que :
2π
1
(f * g ) ( x ) = ------- f ( x – t ) g ( t )d t . (9) ||f ||1 < M sup ε n
2π 0 n
où M est une constante numérique.

Théorème 1. Le produit de convolution a les propriétés
suivantes :
a) f * g ∈ L 1 Si ^ n’est pas surjectif, on a toutefois le théorème fondamental
suivant.
et :
||f * g ||1 < ||f ||1 ||g ||1
b) L’opération * dans L 1 est commutative, associative et distri- Théorème 2 (théorème d’unicité). f → fˆ est un homomor-
butive sur l’addition. phisme injectif de norme 1 de L 1 dans c0 .
c) Si f ∈ L 1 et n ∈ Z :
f * en = cn (f )en Preuve. ◊
E E
2π 2π
d) f ° fˆ est un homomorphisme de l’algèbre L 1 dans 1 – i nt 1
fˆ( n ) = ------- f ( t )e d t < ------- f(t) dt = f ,
l’algèbre c0 des suites ( c n ) n ∈ Z tendant vers zéro à l’infini 2π 0 2π 0
1
( lim c n = 0 ) . donc :
n →∞ fˆ c0 = sup fˆ( n ) < f 1 ,
n
ce qui montre que ^ est de norme au plus 1.
Preuve. ◊ La commutativité s’établit ainsi, à l’aide de la proposi-
tion 1.
Si f est la fonction constante égale à 1 :
E gx E
a) est admis. 2π x
1 1 ||f ||1 = 1 , fˆ (0) = 1,
b) (g * f )(x ) = ------- ( – t ) f ( t )d t = ------- g ( u ) f ( x – u )d u
2π 0 2π x – 2π
E fx d’où fˆ = 1 et ^ est de norme 1.

2π c0
1
= ------- ( – u ) g (u )du = (f * g )(x )
2π 0
■ L’injectivité est plus difficile à établir ; posons, pour N entier
E E >1:
2π 2π
1 in(x – t) i nx 1 – i nt
c) (f * en )(x ) = ------- e f ( t )d t = e ------- e f ( t )d t 1 1 + cos t N
2π 0 2π 0 K N ( t ) = ------  ---------------------- ,
εN 2
= cn (f )en (x )
d) Si l’on utilise le théorème de Fubini [AF 143] (facile à justifier), où εN > 0 est tel que :
on obtient :
E
2π
dt
E E E K N ( t ) ------- = 1
2π 2π 2π
^ 1
f *g ( n ) = ------- ( f * g ) ( x )e
– i nx 1
d x = ---------2 f ( x – t ) g ( t )d t e–inxdx 0 2π
2π 0 4π 0 0
et notons que :
E E 1
2π 2π
1 – i nx ε N > --------- . (10)
= ---------2 g(t) f ( x – t )e dt 4N
4π 0 0
En effet, on a :
E
2π
1 – i nt ˆ
g ( t ) [ 2πe f ( n ) ]d t = fˆ( n ) ĝ ( n ) .
E
= ---------2 2π
1 + cos t N
---------------------- d t
4π 0 1
ε N = -------  
2π 0 2
^ ^
Les propriétés f + g = fˆ + ĝ et λf = λfˆ étant claires, on a le résul-
E E
π π
1 1 + cos t N
 --------------------- 1 1 + cos t N
 ---------------------
tat annoncé (f ° fˆ ), modulo le lemme suivant qui sera établi dans le = --- 0
- d t >  ---
 
-  sint dt
 
π 2 π 0 2
fascicule [AF 143]. ◊
Ex
1
2 N 2 1
= --- d x = ----------------------- > --------- .
Lemme 1 (lemme de Riemann-Lebesgue). Soit f ∈ L 1 [a, b] ; π 0 π(N + 1) 4N
E
alors : b
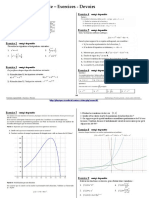
i λt Le graphe de KN a l’allure d’une courbe en cloche de Gauss
lim f ( t )e d t = 0 (λ ∈ R).
λ →∞ a (figure 1).

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
En effet :
E
2π
1
(f * KN )(x ) – f (x ) = ------- [ f ( x – t ) – f ( x ) ] KN (t )dt,
2π 0
kN d’où, en utilisant le théorème de Fubini :
E
2π
−−π π t 1
||f * KN – f ||1 = ------- ( f * KN ) ( x ) – f ( x ) d x
2π 0
E
2π
Figure 1 – Graphe de KN 1
< ------- K N ( t ) g ( t )d t ,
2π 0
où :
E
■ Montrons ensuite les deux propriétés suivantes de KN où δ est un 2π
réel non nul entre 0 et π et g un élément de C 0 : 1
g ( t ) = ------- f(x – t) – f(x) dx .
EK
π 2π 0
N ( t )d t → 0 quand N → ∞. (11) Or, on démontre (continuité de la translation dans L 1) que g ∈ C 0 ;

δ
puisque g (0) = 0, (12) et la majoration précédente donnent bien la
On a : relation (14).
Pour finir, (13) et (14) donnent :
EK E E
π π π
1 + cos t N
 --------------------- 1 + cos δ  N
 -----------------------
N ( t )d t < 4 N - d t < 4N - dt ||f ||1 = 0, c’est-à-dire f = 0 dans L 1
δ δ 2  δ 2 
cela signifie précisément que f est nulle presque partout ; si f est de
1 + cos δ N
< 4 N π  -----------------------  , plus continue, f est nulle partout. ◊
 2 
1 + cos δ
et : ----------------------- < 1 . Le théorème 2 d’unicité est de la plus grande importance :
2 c’est lui qui entraînera, paragraphe 1.4, que (en ) est une base
E
2π
1 hilbertienne de L 2.
------- K N ( t ) g ( t )d t → g ( 0 ) quand N → ∞. (12)
2π 0
Soit, en effet ε > 0, M = ||g ||∞ et δ ∈]0, π[ tel que :

1.4 Cas des séries uniformément
|g (t ) – g (0)| < ε si |t | < δ, convergentes
on a :
Soit ( c n ) n ∈ Z une suite de nombres complexes telle que la suite
E E
2π π
1 1 de fonctions SN , où :
------- K N ( t ) g ( t )d t – g ( 0 ) = ------- K N ( t ) [ g ( t ) – g ( 0 ) ]d t N
2π 0 2π –π
∑ ck e
i kx
SN ( x ) = ,
E EK
δ π –N
1 2M
< ------- εK N ( t )d t + --------- N ( t )d t
2π –δ π δ soit uniformément convergente, ce qui est par exemple le cas si
∞
∑ ck < ∞ à l’aide du critère de Cauchy de convergence uniforme.

EK
π
2M
< ε + --------- N ( t )d t
–∞
π δ Soit f la limite de SN ; f ∈ C 0 et on peut chercher ses coefficients de
Fourier. Le théorème suivant dit qu’on retombe sur les cn et que
< 2ε si N > N0
l’analyse est l’opération inverse de la synthèse ; bien qu’il s’agisse
N
d’après la relation (11).  
de séries à double sens  ∑  , on exprime aussi la convergence
 –N 
■ Reste à montrer que ^ est injectif, autrement dit que fˆ = 0 ∞
∑ ck e
entraîne f = 0, ce qui va résulter des relations (13) et (14) suivantes : i kx
uniforme de SN en disant que la série trigonométrique
–∞
● f * KN = 0. (13) converge uniformément.
KN est de la forme : Théorème 3.

∞
N
∑ ck e
i kx
∑ λk ek a) Soit
–∞
une série trigonométrique uniformément
–N
convergente de somme f (f ∈ C 0). Alors :
donc :
N N cn (f ) = cn , ∀ n ∈ Z .
f * KN = ∑ λk f * ek = ∑ λkfˆ( k ) ek = 0 , b) De même, si une série trigonométrique
–N –N a0 ∞
------ + ∑ ( a n cos n x + b n sin n x ) converge uniformément vers une
d’après le théorème 1. 2
1
fonction f, on a :
● ||f * KN – f ||1 → 0 quand N → ∞. (14) an (f ) = an et bn (f ) = bn , ∀n > 0.

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
Preuve. ◊ (série de Bertrand divergente) et donc qu’une série trigonométrique

a) Fixons n ∈ Z et prenons N > |n | ; nous avons vu, paragraphe 1.1, peut converger uniformément sans converger normalement.
que :
E
2π
1
------- S N ( t )e
– i nt
d t = cn . (15)
1.5 Règles de calcul
2π 0
Les coefficients de Fourier « complexes » cn se prêtent mieux au
Compte tenu de la convergence uniforme de SN vers f, le passage
calcul que les coefficients an , bn pour une raison précise : l’équation
à la limite dans la relation (15) donne :
fonctionnelle de la fonction exponentielle :
E
2π
1 – i nt ea+b = ea · eb
------- f ( t )e d t = cn ,
2π 0
est plus simple que les équations fonctionnelles des fonctions cosi-
autrement dit : cn (f ) = cn . nus et sinus, exprimées par les formules d’addition de la trigono-
b) Se prouve de même. ◊ métrie.
Nous nous limiterons donc aux cn , étant entendu qu’on revient
On démontre que le théorème 3 reste valable si SN (t ) facilement aux an , bn à l’aide de la proposition 1 ; pour f ∈ L 1 et
converge simplement vers f (t ), sauf peut-être sur un ensemble a ∈ R , on pose :
dénombrable D et si de plus f ∈ L 1 ; c’est par exemple le cas fa (t ) = f (t + a ).
pour la série :
∞ Certaines des relations qui suivent sont déjà dans le d) du théo-
cos nt
∑ ----------------
ln n
= C ( t ) (t ≠ 2k π), rème 1.
2 Proposition 2
mais ce n’est plus le cas pour la série partout convergente :
∞ Soit f, g ∈ L 1, a ∈ R , k ∈ Z ; alors :
sin n t
∑ --------------
ln n
- = S(t) a) cn (f + g ) = cn (f ) + cn (g ) et cn (λf ) = λcn (f )
2
car cette fois S ∉ L1 (S se comporte comme t –1(ln t –1)–1 quand b) cn (f * g ) = cn (f )cn (g )
> c) cn (fa ) = einacn (f )
t → 0 ).
Mais la preuve de ce nouveau théorème est fort difficile, d) cn (ekf ) = cn –k (f )
même quand D = ∅ et f = 0 [3]. e) cn (f (k) ) = (in ) kcn (f ) si k ∈N et f ∈C k.
∞
Application. Soit α > 0 et f une fonction de la classe de Gevrey
∑ an z
n
Exemple 1Soit F (z ) = la somme d’une série entière de
d’indice α, c’est-à-dire 2π – périodique indéfiniment dérivable et
0
rayon de convergence > 1 ; alors si 0 < r < 1 : vérifiant des inégalités de la forme (où a, b > 0) :
 1
E |f (k )(x )| < abk(k !)α.
2π
 ------- it
F (r e )e
– i nt
d t = an r
n
si n>0
 2π 0 (16)
Alors, les coefficients de Fourier de f vérifient des inégalités de la

 et = 0 si n < 0. forme :
∞ |cn(f )| < a’exp(–b’|n |1/α). (19)
∑an r
n i nt
En effet, la série trigonométrique e converge normale-
En effet :
0
ment, donc uniformément vers F (r eit ). |cn(f )| = |n |–k |cn(f (k ) )| < |n |–k ||f (k )||∞
Exemple 2Soit : ∞ < |n|–k ab k k kα ;

sin nt
f ( t ) = ∑ -------------- ; on optimise approximativement cette inégalité en prenant
n ln n
alors : 2
n 1⁄α
1 k =  ------ , où [ ] désigne la partie entière, ce qui donne la rela-
b n (f ) = ------------ pour n>2. (17) e
n ln n tion (19) pour des constantes (> 0) a ’, b ’ convenables.
En effet, on verra dans le paragraphe 2.1 que :
N
sin n t
∑ -------------
n
- <C (18)
où C est une constante numérique.

1
2. Développement en série
En écrivant :
de Fourier
-------------- = ε n  -------------- ,
sin n t sin nt
n ln n  n 
où εn = (lnn ) –1, on voit alors que le critère d’Abel uniforme s’applique 2.1 Noyau de Dirichlet
∞
sin nt
et que la série ∑ -------------- converge uniformément, donc (17) résulte du N
n ln n
∑e
i nt
2 Pour N > 0, posons D N ( t ) = ; DN s’appelle le noyau de
théorème 3.
–N
Remarquons au passage que : Dirichlet d’ordre N ; c’est lui qui va régir le comportement de SN (f ),
∞
comme le montre le théorème suivant, où f ∈ L 1.
∑ ( n ln n )
–1
||sin nt ||∞ = 1 et =∞
2 Preuve. ◊

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
où rN (t ) est une quantité uniformément bornée. Enfin, un change-

Théorème 4. Soit t réel tel que 0 < |t | < π ; alors : ment de variable et une intégration par parties montrent que :
sin  N + --- t
E E E
1 t Nt Nt
 2 sin Nu sin v 1 – cos Nt 1 – cos v
------------------ d u = ------------d v = --------------------------- + -dv ,
----------------------
a) D N ( t ) = ------------------------------------- 0 u 0 v Nt 0 v
2
sin ---  t
 2
1 – cos x
et cette quantité est uniformément bornée puisque ----------------------- est
x
sin Nt
E E
b) DN (t ) = 2 ---------------- + u (t )sinNt + cosNt, Nt ∞
t + 1 – cos v 1 – cos v
borné sur R et - d v majoré par
----------------------
2
-dv = π . ◊
----------------------
2
où u est une fonction bornée. 0 v 0 v
c) SN (f ) = f * DN .
2N ( 2 N + 1 )i t
2.2 Théorème de Dirichlet
e –1
∑e
– iNt i nt – i Nt
a) D N ( t ) = e = e --------------------------------
-
0
it
e –1 Supposons maintenant que f ∈ L 1 a, au voisinage de x0 ∈ R , un
comportement relativement régulier, au sens où :
 N + --1- i t +
 2
(*) lim f ( x ) = f
2i sin   N + --- t sin   N + --- t
1 1 >
e x → x0
– i Nt  2   2 
=e -----------------------------------------------------------------
t
= -.
------------------------------------ et :
i ---  t
2
e 2i sin ---  t sin ---
 2 lim f ( x ) = f
–
 2 < x
x→ 0
existent (f possède une limite à droite et une limite à gauche en x0) ;

sin Nt cos  --- + sin  --- cos Nt
t t
 2  2 t f(x) – f
+
+
b) D N ( t ) = ------------------------------------------------------------------------------- = sin Nt cotg --- + cos Nt (**) lim --------------------- = ,
 t 2 > x – x0
sin --- x → x0
 2
et :
–
= sinNt  --- + u ( t ) + cosNt , où u est bornée. f(x) – f
2 –
t  lim --------------------- = ,
< x – x0
x → x0
c) D’après le théorème 1 : existent (f est en un certain sens dérivable à droite et dérivable à

gauche en x0).
N N
Sous ces hypothèses, on a le théorème suivant, qui est historique-
SN ( f ) = ∑ cn (f ) en = ∑f * en ment le premier théorème de convergence des séries de Fourier
–N –N démontré rigoureusement.
N
 
= f *  ∑ e n = f * D N . ◊ Théorème 5 (théorème de Dirichlet ponctuel). Si la fonc-
 –N  tion f vérifie (*) et (**), on a :
1
Un corollaire de l’étude du noyau de Dirichlet est la preuve de lim S N ( f , x 0 ) = --- (f + + f –). (20)
N→∞ 2
l’inégalité (18).
Corollaire 1. Schéma de preuve. ◊ On peut supposer x0 = 0. Le théorème 4

et la parité de DN nous donnent :
Il existe une constante numérique C telle que :
E
π
1 1 + –
N SN (f, 0) – --- (f + + f –) = ------- [ f ( t ) + f ( – t ) – f – f ] DN (t )dt
sin nt
∑ --------------
n
- <C. 2 2π 0
Eht
1
π
( ) sin  N + --- t d t ,
1
=
Preuve. ◊ On peut supposer que 0 < t < π.  2
0
N où :
Puisque D N ( t ) = 1 + 2 ∑ cos nt , + –
f ( t ) – f + f ( –t ) – f
1 h ( t ) = ------------------------------------------------- (0 < t < π) .
2π sin  ---
t
on a :  2
E E
N t t Les hypothèses (*) et (**) entraînent l’intégrabilité de h sur
sin nt 1 sin Nu
∑ --------------
n
- = ---
2 0
[ D N ( u ) – 1 ]d u =
0
------------------ d u + r N ( t ) ,
u [0, π], et le lemme 1 (lemme de Riemann-Lebesgue) donne la
1 conclusion. ◊

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
Soit a ∈ C\ Z et f la fonction de L 1 définie par :
f (t ) = eiat si – π < t < π ; x0 = π.

g
On voit que (*) et (**) sont vérifiées avec :
0
I 2π
f – = eia π ; , = ia eia π ; f + = e–ia π ; , = ia e–ia π
– +
J
–i a π
(par exemple : lim f ( x ) = lim f ( x – 2π ) = lim f ( y ) = e ).
> > >
x →π x →π y → –π Figure 2 – Hypothèses pour démontrer le principe de localisation
de Riemann
On a, d’autre part :
E
π
1 i at –i nt n sin π a Preuve. ◊
c n (f ) = ------- e e d t = ( –1 ) -------------------- ,
2π –π π(a – n)
■ Montrons d’abord comment le théorème 7 entraîne le théo-
d’où : rème 6.
N N
in π sin π a a) Soit g ∈ C 1, égale à 1 sur I et égale à 0 sur [0, 2π] \ J (figure 2) ;
S N ( f, π ) = ∑ cn (f )e = ∑ --------------------
π(a – n) l’hypothèse sur f entraîne que fg = 0.
–N –N
Le théorème 7 entraîne donc que g SN (f ) → 0 uniformément sur
N R , a fortiori sur I ; mais :
sin π a 2 a sin π a 1
= --------------- + ----------------------
πa π ∑ -----------------
2 2 . g (x )SN (f , x ) = SN (f , x ) pour x ∈ I,
1 a – n
Le théorème de Dirichlet donne donc : d’où le résultat.
∞
sin π a 2 a sin π a 1 1 + – b) Se déduit de a) en considérant f – g.
--------------- + ----------------------
πa π ∑ -----------------
2 2
= --- ( f + f ) = cos π a ,
2
1 a –n
■ Voici le principe de la preuve du théorème 7 ; fixons g et
formule qu’on écrit plutôt sous la forme : posons :
∞ TN (f ) = SN (fg ) – gSN (f ) ;
1 1
π cot π a = --- + 2 a ∑ ----------------- .
a 2 2 nous avons :
a –n 1
E fxt
π
1
Il est logique de se demander ce qui se passe si f se comporte bien TN (f , x ) = ------- ( – ) [g (x – t ) – g (x )] DN (t ) dt ;
2π –π
non seulement en x0 , mais sur tout un intervalle I (c’est-à-dire véri-
fie (*) et (**) pour tout x0 ∈ I ). On pourrait alors espérer que SN (f , x ) Le théorème des accroissements finis (où M = ||g ’||∞) et le théo-
converge uniformément sur I ; c’est ce qui se passe, comme on va le rème 4 montrent que :
voir dans le paragraphe suivant.
1
|g (x – t ) – g (x )| |DN (t )| < M |t | --------------------- < M π,
sin  ---
t
 2
2.3 Principe de localisation de Riemann d’où :
et retour à Dirichlet
E
π
1
|TN (f , x )| < M π ------- f ( x – t ) d t = M π||f ||1,
Riemann a mis en évidence le fait que le comportement de SN (f ) 2π –π
au voisinage d’un point x0 ne dépend que du comportement de f au puis :

voisinage de x0 , ce qui n’a rien d’évident a priori puisque les coeffi-
cients de Fourier de f font intervenir son intégrale sur tout le seg- ||TN (f )||∞ < M π ||f ||1 .
ment [0, 2π]. De façon précise, on a le résultat suivant.
Les applications linéaires TN : L 1 → C 0 sont donc uniformément
bornées en norme ; de plus :
Théorème 6 (principe de localisation de Riemann). Soit
f, g ∈ L 1 et J un intervalle de [0, 2π]. TN (ek ) = SN (gek ) – gek
a) On suppose f nulle sur J ; alors SN (f ) converge vers zéro
pour N > |k |, et gek ∈ C 1, donc SN (gek ) → gek uniformément,
uniformément sur tout segment I intérieur à J.
comme nous le verrons indépendamment au paragraphe 4 ; donc,
b) On suppose f et g égales sur J ; alors, SN (f ) – SN (g ) TN (ek ) → 0 dans C 0 ; de plus, la relation (14) montre que l’espace
converge vers zéro uniformément sur tout segment I intérieur vectoriel V engendré par les ek est dense dans L 1 (car f * KN ∈ V ), et
à J. le théorème 7 s’ensuit. ◊
Une importante application du principe de Riemann est donnée
par le théorème suivant.
La preuve du théorème 6 est une conséquence facile du résultat
suivant, dû à Steinhaus.
Théorème 8 (théorème de Dirichlet local). Soit f ∈ L 1, de

Théorème 7. Si f ∈ L 1 et g ∈ C 1, alors : SN (fg ) – g SN (f ) → 0 classe C 1 sur un intervalle J de [0, 2π] ; alors : SN (f, x ) → f (x )
uniformément sur R . uniformément sur tout segment I intérieur à J.

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
Preuve. ◊ Soit J 1 un intervalle ouvert, tel que I ⊂ J 1 ⊂ J , et ■ Soit, maintenant, γ un arc fermé du cercle de convergence ne
g ∈ C 1, égale à f sur J 1 ; on a alors : contenant pas 1 :
SN (f ) – SN (g ) → 0 uniformément sur I, γ = {eix ; a < x < b , 0 < a < b < 2π}
et :
SN (g ) → g uniformément sur R , et f est de classe C 1 sur ]0, 2π[, donc le théorème de Dirichlet local
(théorème 8) entraîne la convergence uniforme de SN (f, x ) sur [a, b],
en particulier : ∞
∑ an u
n
SN (f, x ) → g (x ) = f (x ) uniformément sur I. ◊ autrement dit la convergence uniforme de pour u ∈γ.
0
Un cas particulier important, dont nous nous sommes servis On peut montrer (par une analyse directe de SN (f, 0)) que la série
dans la preuve du théorème 7, et qui sera prouvé plus tard (théo- ∞
rème 14), est le suivant.
∑ an converge avec pour somme 0.
0
Le théorème de convergence non tangentielle d’Abel [4] entraîne la

Théorème 9 (théorème de Dirichlet global). Si f (ou ∈C 1 ∞
même si f ∈ C 0 est C 1 par morceaux), la série de Fourier de f est
∑ an z
n
normalement, en particulier uniformément, convergente. convergence uniforme de sur tout secteur :
0
|1 – z | < C (1 – |z |) ;
∞ ∞
F ( z ) = exp  ------------ =
z+1
∑ an z ∑ an z
n n
, |z | < 1 mais il n’y a pas convergence uniforme de sur le cercle
z–1
0 0
1 1
(l’existence des an vient de la théorie des fonctions holomorphes). z – --- = --- , tangent intérieurement en 1 au cercle unité (soit δ ce cer-
2 2
∞
z+1
∑ an z cle). En effet, l’homographie z ° ------------ transforme δ en une droite per-
n
On se propose de montrer que la série entière , de rayon de z–1
0 pendiculaire à l’axe réel en –1, donc en la verticale 5 w = –1, d’où :
convergence 1, converge uniformément sur tout arc γ (fermé) du cer-
cle de convergence qui ne contient pas 1. ∞
= exp  5 ------------ = e
z+1
∑ an z
n –1
si z ∈ δ et z ≠ 1,
 z – 1
■ Notons, d’abord, que : 0
∞ ∞
 1 – z 2
∑ an = 0 , ce qui exclut la convergence uniforme de ∑ a n z
n
F ( z ) = exp  – ----------------2- <1 , alors que
 1 –z  0 0
sur δ et fournit un bel exemple du caractère optimal du théorème
et que : d’Abel.
it
lim F (r e ) = f ( t ) ,
<
r→1
avec f ( t ) = exp – icot --- si 0 < t < 2π ; f (0) = 0.

t
 2 3. Exemples
■ Ensuite, la relation (16) nous donne : de développement
 1
E en série de Fourier
2π
 ------- it
F (r e )e
–i nt
d t = an r
n
pour n>0
 2π 0

 et = 0 pour n<0
< 3.1 Cas des fonctions paires ou impaires
Le passage à la limite, quand r → 1 , justifié par l’emploi du théo-
rème de convergence dominée de Lebesgue (|F (r e it )| < 1) conduit à :
Proposition 3
 1
E
2π
 ------- f ( t )e
–i nt
d t = an pour n>0 Soit f ∈ L 1 , an = an (f ) , bn = bn (f ) , cn = cn (f ).
 2π 0 (21)
 a) Si f est paire, on a bn = 0
 et = 0 pour n < 0
et : a N N
N S N ( f , x ) = -----0- + ∑ a n cos nx = c 0 + 2 ∑ c n cos nx .
2
∑ an e
i nx
Autrement dit = S N ( f , x ) et la série entière devient, sur 1 1
0 b) Si f est impaire, on a an = 0
son cercle de convergence, une série de Fourier (la remarque en est
et : N N
souvent utile).
SN ( f , x ) = ∑ bn sin nx = 2i ∑ c n sin nx .
1 1
C’est une vérification facile ; mais la proposition 3 se révèle utile

dans la pratique.

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
3.2 Fonction signal. Fonction triangle Autrement dit, on a :

ε
σε * σε = --- ∆ 2 ε ,
■ Soit ε ∈]0, π[ et σε ∈ L 1 la fonction signal (figure 3) définie par : π
d’où :
σε (t ) = 1 si |t | < ε, 2π
∆ ε = ------- σε/2 * σε/2 (0 < ε < π).
=0 si ε < |t | < π. ε
Il en résulte que :
Le signal σε est pair, donc :
2
2π 2 2π sin n ( ε ⁄ 2 )
2ε c n ( ∆ ε ) = ------- 1 c n ( σ ε ⁄ 2 )2 = ------- -----------------------------
-,
a 0 ( σ ε ) = ------ , ε ε n π
2 2
π
soit :
E
ε
1 2 sin nε 1 – cos n ε
a n ( σ ε ) = --- cos nt d t = ------------------- pour n > 1, c n ( ∆ ε ) = -------------------------- ;
π –ε nπ n πε
2
et : ε
N avec c 0 ( ∆ ε ) = ------- .
ε sin nε cos nx 2π
S N ( σε , x ) = --- + 2 ∑ ----------------------------------- .
π nπ D’après la proposition 3, on a :
1
Le théorème de Dirichlet ponctuel (théorème 5) s’applique en N

ε 1 – cos nε
+ – + –
x0 = ε avec σ ε = 0, σ ε = 1, , = , = 0, d’où : S N ( ∆ ε , x ) = ------- + 2 ∑ --------------------------
2
cos nx .
2π n πε 1
∞
ε sin 2 nε 1 Le théorème de Dirichlet global (théorème 9) s’applique à ∆ ε , qui
--- + ∑ ------------------- = --- ,
π nπ 2 est C 1 par morceaux (on voit d’ailleurs que sa série de Fourier est
1
normalement convergente), d’où :
soit encore en posant 2ε = α :
∞
∞ ε 1 – cos nε
sin nα π–α ∆ ε ( x ) = ------- + 2 ∑ -------------------------- cos nx , ∀ x ∈ R.
∑ ----------------
n
- = -------------
2
si 0 < α < 2π . 2π n πε
1
2
1
x = 0 et ε = π donnent :
■ Soit ∆ε ∈ L 1 la fonction triangle (figure 4) définie par : ∞
1 4 1
--- = -----2- ∑ -----------------------2- ,
2 π
∆ ε (t ) = max  1 – ----,0 pour |t | < π . 0 (2p + 1)
t
ε d’où :
π ∞
Calculons d’abord, pour 0 < ε < --- , la convolution σε * σε . Cette 1 π
2
convolution est paire, nulle sur [2ε, π]. 2 ∑ -----------------------2-

= ------
8
0 (2p + 1)
Pour 0 < x < 2ε on a : et :
E E
π ε ∞ ∞ 2
1 4 1 π
1
σε * σε (x) = -------
2π 2π
1
σ ε ( x – t ) σ ε ( t )d t = -------
–ε
σ ε ( x – t ) dt ∑ -------2 = --- ∑ -----------------------2- = ------ .
3 (2p + 1) 6
–π 1 n 0
E E
x+ε ε
1 1
= ------- σ ε ( u )du = ------- du
2π x–ε 2π x–ε 3.3 Fonction |cos|.
2ε – x ε Théorème de Weierstrass
= --------------- = ---  1 – -------
x
2π π 2ε  Si f (t ) = |cost |, f est paire et ∈ C 0, donc les bn (f ) sont nuls et :
E E
π π
1 2
a n (f ) = --- cos t cos nt dt = --- cos t cos n t dt
π π
σε –π 0
E E
π⁄2 π
2
= --- cos t cos nt dt – cos t cos nt dt
--π --ε ε π π 0 (π ⁄ 2)
E
π⁄2
2 n
Figure 3 – Définition de la fonction signal = --- 11 + ( –1 ) 2 cos t cos nt dt ,
π 0
en faisant le changement de variable t = π – u dans la seconde

intégrale ; d’où :
a2n + 1(f ) = 0
∆ε et :
E
π⁄2
2
a 2 n (f ) = --- [ cos ( 2 n + 1 ) t + cos ( 2 n – 1 ) t ] dt
π 0
--π --ε ε π n–1
2 sin ( 2 n + 1 )π ⁄ 2 sin ( 2 n – 1 )π ⁄ 2 4 ( –1 )
= --- ------------------------------------------ + ------------------------------------------ = --- -.
--------------------
π 2n + 1 2n – 1 π 4n – 1
2
Figure 4 – Définition de la fonction triangle

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
Le théorème de Dirichlet global (théorème 9) et la proposition 3 QN est un polynôme de degré au plus N et la relation (23) montre
donnent : que :
∞ n–1
2 4 ( –1 ) 4 1
< --- ∑ ------------------
2  ----------------
1
– -----------------
1
π n > N 4 n 2 – 1 π n∑
f ( t ) = cos t = --- + --- ∑ --------------------
- cos 2 nt , t ∈ R . (22) F – QN ∞
- = ---
 2 n – 1 2 n + 1
π π 4n 2 – 1 > N
1 0 0
■ Considérons maintenant la fonction F définie sur [–1, 1] = I par 2 1 2

= --- -------------------- < --------- ;
F (x ) = |x | et cherchons à l’approcher uniformément sur I par une π 2 N0 + 1 π N
suite de polynômes. Une façon de procéder est d’utiliser le dévelop-
pement binomial fractionnaire : la relation (24) en découle.
∞
Plus généralement, étant donné F continue sur [–1, 1], on appelle
série de Fourier-Tchebycheff de F la série :
1 – u = 1 – ∑ an u
n
pour – 1 < u < 1,
0 ∞
a
-----0- + ∑ a n T n (25)
 an  2
1
où an est équivalent à cn –3/2 - → 1 quand n → ∞ , c étant
 -------------------
–3 ⁄ 2
 cn  où an = an (f ) et f (t ) = F (cost ) (f est une fonction paire).
une constante > 0.
Les sommes partielles de (25) fournissent souvent d’excellentes
Nous obtenons, pour x ∈ I : approximations polynomiales de F [1] et d’un point de vue plus
∞
théorique une légère modification de (25) conduit au résultat sui-
2 n vant.
1 – ( 1 – x ) = 1 – ∑ an ( 1 – x )
2
x =
0
et F est limite uniforme sur I des polynômes PN , où : Théorème 10 (théorème de Weierstrass). Toute fonction F
N continue sur un segment [a, b] est limite uniforme sur ce seg-
2 n
PN (x ) = 1 – ∑ an ( 1 – x ) ; ment d’une suite de polynômes.
0
mais cette approximation n’est pas très bonne ; en effet : Schéma de preuve. ◊ Soit λ : [–1, 1] → [a, b] une bijection
Et
∞ ∞ affine.
–3 ⁄ 2 –1 ⁄ 2
F – PN ∞
= sup F ( x ) – P N ( x ) =
x∈I
∑ an ∼ c d t = 2 cN , Si on peut approcher F s λ par un polynôme P, on peut approcher
N+1 N F par le polynôme P s λ –1.
donc la vitesse d’approximation de F par des polynômes de degré Il suffit donc de traiter le cas a = –1, b = 1.
au plus 2N (le degré d’un polynôme mesurant la complexité de ce Soit de nouveau :
polynôme), ici les PN , est de l’ordre de N –1/2. f (t ) = F (cost ) ;
■ Rappelons, de plus, qu’il existe une suite ( T n ) n > 0 de polynômes f est limite uniforme de fN , où fN = f * KN et où KN est comme dans
de degré n, appelés polynômes de Tchebycheff, et tels que : la preuve du théorème 2, (cf. relation (12)) ; fN est paire et de la
N
Tn (cost ) = cosnt ;
forme ∑ cn , N cos n t ; si donc :
cette suite est définie par les relations de récurrence : 0
T0 (x ) = 1 ; T1 (x ) = x ; Tn + 1(x ) + Tn – 1(x ) = 2x Tn (x ) ; N
qui suivent la formule :

QN ( x ) = ∑ cn , N Tn ( x ) ,
0
cos(n + 1) t + cos(n – 1)t = 2 cosnt cos t .
F est limite uniforme de la suite de polynômes QN , puisqu’on a :
Observons que la relation (22) se lit aussi :
sup F ( x ) – Q N ( x ) = sup F ( cos t ) – Q N ( cos t ) = f – f N ∞
. ◊
∞ n–1 x ∈ [–1,1] t ∈R
2 4 ( –1 )
F ( x ) = --- + --- ∑ --------------------
- T ( x ) , x ∈ I. (23)
π π 4 n 2 – 1 2n
1
■ Posons EN = inf{||F – P ||∞ }, où ∞ = sup et où P parcourt les

x ∈I
polynômes de degré (complexité) au plus N ; nous allons voir que :
2 –1
4. Cas des fonctions
E N < --------- = 0 ( N ) , (24)
πN localement de carré
ce qui, d’une part, est bien meilleur que le N –1/2 obtenu avec les PN , intégrable
et, d’autre part, se révèle être le bon ordre de grandeur pour EN .
Posons, pour cela :
N N 1
4.1 Base des exponentielles imaginaires
N 0 = ---- > ---- – --- (où [ ] est la partie entière)
2 2 2
et : Soit L 2 l’ensemble des fonctions f ∈ L 1 telles que :
N0
E
n–1
2 4 ( –1 ) b
Q N = --- + --- ∑ --------------------
-T ; 2
π π 4 n 2 – 1 2n f ( t ) d t < ∞ pour tous a, b ∈ R (a < b ) ;
1 a

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
L 2 est un sous-espace vectoriel strict de L 1 et ||f ||1 < ||f ||2 pour rier et, en opposition au théorème 1, l’application f ° fˆ est une
f ∈ L 2 (inégalité de Cauchy-Schwarz) où on pose : 2
isométrie surjective de L 2 sur l’espace , des suites (cn ) telles que
E ∑ cn
2π 1⁄2 2
< ∞.
=  ------- f ( t ) d t
1 2
f 2  2π
;
0
On n’a rien de tel pour l’espace C 0 des fonctions continues
|| ||2 s’appelle la norme L 2 et elle est associée au produit scalaire : 2π – périodiques par exemple et on peut montrer le théorème
suivant.
E
2π
1
( f ⁄ g ) = ------- f ( t )g ( t )d t ,
2π 0
Théorème 13. Soit c = (cn ) ∈ , , et ||c ||2 =
2
( ∑ cn 2 )1 ⁄ 2 ;
qui fait de L 2 un espace de Hilbert ; la complétude de L 2 pour || ||2
n’est pas évidente ; elle découle du théorème de Riesz-Fischer que alors, on peut trouver f ∈ telle que : C0
nous admettrons ici. a) fˆ ( n ) > c , ∀n ∈ Z ;
n
Les formules de Fourier ont une interprétation agréable en termes b) ||f ||∞ < M ||c ||2 (où M est une constante numérique).
du produit scalaire de L 2 ; on a, en effet, de façon évidente :
cn (f ) = (f/en ) pour f ∈ L 2. (26)

Ce théorème, dû à Kahane Katznelson, De Leeuw (1980) a vu sa
Le théorème suivant est fondamental. preuve récemment simplifiée par Nazarov (1995). Il montre, en par-
ticulier, qu’on ne peut rien dire de mieux sur la taille des coefficients
de Fourier d’une fonction de C 0 que sur celle des coefficients d’une
fonction de L 2 ; la différence entre L 2 et C 0 se fera de façon compli-
Théorème 11. Les fonctions en (n ∈ Z ) forment une base
quée au niveau des arguments des cn (f ).
orthonormale (on dit aussi hilbertienne) de l’espace de Hilbert
L 2. Exemple 1Dans l’exponentielle apériodique (eiat ) considérée précé-
demment (§ 2.2), prenons a ∈ R\Z ; alors :
Preuve. ◊ L’orthonormalité des en vient de la relation (3). |f (t )| = 1 ∀ t et ||f ||2 = 1.
Selon la théorie générale des espaces de Hilbert, montrer qu’elles L’identité de Parseval donne donc :
forment une base revient à montrer que :
∞
sin π a 2
(f /en ) = 0 ∀ n ∈ Z ⇒ f = 0. 1 =  --------------- ∑ -------------------2 ,
(27) 1
 π 
– ∞ (a – n)
Or, si f ∈ L 2, l'hypothèse de la relation (27) se lit aussi fˆ = 0,
puisqu’on a L 2 ⊂ L 1. soit encore :
∞
Le théorème d’unicité 2 donne donc f = 0. ◊ π 2
 ----------------- 1
 sin π a
- = ∑ -------------------2 ( a ∈ R\Z ) . (28)
–∞ (a – n)
4.2 Inégalité de Bessel. Exemple 2Changeons a en ia (a > 0) dans l’exponentielle

Identité de Parseval considérée ; on a alors :
|f (t )| = e–at | si |t | < π,
Le théorème 11 et la théorie des espaces de Hilbert ont d’impor- d’où :
tantes applications aux séries de Fourier, comme l’exprime le théo- 2 sh2π a
rème suivant. f 2 = ----------------- ,
2π a
et l’identité de Parseval donne :
Théorème 12
2 ∞
a) Si f ∈ L 2, on a : sh2π a sh π a 1
----------------- = ---------------
2π a 2
- ∑ -------------------2 ,
π –∞ ia – n
1⁄2
( ∑ cn (f ) 2 ) < f 2 (inégalité de Bessel) ;
soit encore :
en particulier : ∑ c n (f ) < ∞ . ∞
2
1 π
∑ -----------------
2
- = --- coth π a .
2 a
(29)
b) Si f ∈ L 2, on a plus précisément : –∞ n +a
>
1⁄2 Quand a → 0 , on a notoirement :
( ∑ cn (f ) 2 ) = f 2 (identité de Parseval).
1 πa 2
∞ coth π a = ------ + ------ + 0 ( a ) ,
πa 3
c) Réciproquement, si ∑ c n < ∞ , il existe une unique fonction
2
–∞ et l’équation (29) se lit :

f ∈ L 2 telle que :
∞ 2
cn (f ) = cn , ∀ n ∈ Z . 1 1 1 π
----2- + 2 ∑ -----------------
2
- = ----2- + ------ + 0 ( a ) .
2
a 1 n + a a 3
On voit donc que l’appartenance d’une fonction à L 2 se lit entière-

ment sur la taille (c’est-à-dire le module) de ses coefficients de Fou-

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
1
Après simplification par -----2- , il vient : 4.4 Retour au théorème de Weierstrass
a
∞ 2 La théorie des espaces de Hilbert et le théorème 11 entraînent en
π
2∑ n
–2
= ------ particulier le théorème suivant
3
1
et on retrouve la célèbre relation : Théorème 15. Si f ∈ L 2 et N > 0, SN (f ) est la meilleure

∞ 2 approximation en moyenne quadratique (c’est-à-dire en norme
π
∑n
–2
= ------ . L 2) de f par des polynômes trigonométriques de degré < N
6 N
1
(c’est-à-dire par des fonctions de la forme ∑ λn en , λn ∈ C ).
–N
4.3 Fonctions de classe C 1

et convergence normale Soit, en effet, V le sous-espace de L 2 engendré par les en , où
|n | < N ; f – SN (f ) est orthogonal à V puisque, si |n | < N :
Voici une application plus théorique de l’inégalité de Bessel (théo-
((f – SN (f ))/en) = (f /en) – (SN (f )/en) = cn (f ) – cn (f ) = 0.
rème 12), qui donne notamment la preuve du théorème de Dirichlet
global (théorème 9). On voit donc que SN (f ) est la projection orthogonale de f sur V.
Le point de vue hilbertien et le théorème 15 expliquent heuristi-
Théorème 14. Soit f une fonction de C 0 et cn = cn (f ). quement pourquoi les sommes partielles de la relation (25) donnent
souvent une bonne approximation uniforme sur [–1, 1] de F par des
a) Si ∑ cn < ∞ , alors : polynômes de degré au plus N ; en effet, la relation (4) s’écrit
encore :
∞
∑ cn e E
i nx π
f (x) = , ∀x ∈ R . dt 1
–∞ cos pt cos qt ------ = --- δ p,q si p, q ∈ N∗,
0 π 2
b) Si f est C 1 par morceaux, on a :
soit, en faisant le changement de variable x = cos t :
∑ cn <∞,
E
1
dx 1
et donc : T p ( x ) T q ( x ) ----------------------- = --- δ p,q ;
–1 2 2
∞ π 1–x
∑ cn e
i nx
f (x) = .
–∞
autrement dit, les polynômes T0 , 2 Tn (n > 1) forment une base
orthonormale de l’espace de Hilbert L 2(µ), où µ est la mesure de pro-
Preuve. ◊ dx
babilité ----------------------- .
a) L’hypothèse et le théorème 3 entraînent la convergence nor- 2
π 1–x
∞
∑ cn e
i nx
male, donc uniforme, de la série trigonométrique vers une a N
–∞ La somme partielle -----0- + ∑ a n T n représente donc, la meilleure
2 1
fonction g ∈ C 0 telle que cn (g ) = cn pour tout n. On a donc :
approximation de F dans L 2(µ ) par des polynômes de degré < N ; il
fˆ = ĝ , n’est donc pas trop étonnant que cette somme partielle soit égale-
ment proche de la meilleure approximation en norme uniforme,
et le théorème d’unicité 2 donne : d’autant que les polynômes de Tchebycheff oscillent beaucoup sur
[–1, 1].
f = g.
b) f ’∈ L 2
et la relation cn (f ’) = in cn (f ) de la proposition 2 est
encore valable pour f C 1 par morceaux.
L’inégalité de Cauchy-Schwarz et celle de Bessel donnent alors 5. Équation de la chaleur
pour N entier > 1 :
pour une barre finie
1⁄2
 N –2  2 1⁄2
∑ cn <  2 ∑ n   ∑ c n (f ′) 
0 < n <N  1  0 < n <N
5.1 Modélisation du problème
π
< ------- f ′ 2,
3 Considérons une barre métallique de longueur L, assimilée au
segment [0, L], et appelons u (x, t ) la température du point d’abs-
d’où en faisant tendre N vers l’infini : cisse x à l’instant t, sachant que les extrémités de la barre sont en
contact avec l’extérieur (elles sont froides) et que, à l’instant zéro, le
∞
π point d’abscisse x est porté à la température h (x ).
∑ cn < c 0 + ------- f ′
3
2 .
Comment la barre va-t-elle se refroidir, autrement dit comment va
–∞
évoluer u (x, t ) ? Cette évolution se fait suivant la loi du refroidisse-
Pour conclure, il n’y a plus qu’à appliquer a. ◊ ment de Newton, ce qui, en omettant les constantes physiques et en

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
2
posant Ω = ]0, L[ × ]0, ∞[ (Ω est un ouvert du plan R ), conduit au
problème suivant :
h
−−π 0
u (0, t ) = u (L, t ) = 0 pour t > 0 (conditions aux limites) (30)
π
H
u (x, 0) = h (x ) où h (0) = h (L ) = 0 (conditions initiales) (31)
et où h ∈ C 0 ([0, L]).
2 Figure 5 – Fonction H impaire 2π – périodique
∂ u ∂u
---------2 = ------- sur Ω (équation d’évolution) (32)
∂x ∂t
et u ∈ C 2(Ω ) ∩ C 0 (Ω ) . vérifie aussi (30) et (32) et le principe est de considérer des

combinaisons linéaires infinies : on retrouve l’idée d’obtenir toutes
La fonction u doit donc être solution d’une certaine équation aux les fonctions 2π – périodiques comme superposition infinie de
dérivées partielles (dite équation de la chaleur) et vérifier des condi- signaux élémentaires. Prolongeons d’abord h en une fonction H
tions initiales et des conditions aux limites ; telle est la modélisation impaire 2π – périodique (figure 5), en posant :
du problème.
D’un point de vue mathématique se posent maintenant les ques- H (x ) = h (x ) si 0 < x <π;
tions d’existence et d’unicité de u vérifiant les relations (30), (31)
et (32). H (x ) = – h (– x ) si –π < x <0;
H (x + 2π) = H (x ).
5.2 Séparation des variables Si on cherche u sous forme d’une combinaison infinie :
et séries de Fourier ∞
Cherchons d’abord une solution de l’équation (32) sous forme u (x, t ) = ∑ bn sinnx exp(– n2t ),
d’une fonction à variables séparées : 1
u (x, t ) = f (x ) g (t ) la relation (31) donne :

Il nous faut avoir :
∞
f ”(x ) g (t ) = f (x ) g’ (t ), u (x, 0) = ∑ bn sinnx = H (x ),
soit encore : 1
f ′′ ( x ) g′(t) ce qui suggère de prendre pour les bn les coefficients de Fourier
--------------- = ------------ = constante .
f(x) g(t) de H :
La nécessité de vérifier (30) conduit à prendre la constante de la
E Eht
π π
forme –ω 2, où ω > 0, et donne (puisque f (0) = 0) : 1 2
bn = bn (H ) = --- H ( t ) sin nt d t = --- ( ) sin nt d t . (34)
f (x ) = C te X sinω x, π –π π 0
–ω t
2
Cependant, cette façon de procéder est un peu arbitraire et rien ne
g (t ) = C te X e ,
dit qu’on n’a pas laissé échapper une ou plusieurs solutions ; d’autre
soit : part, des problèmes de convergence de la série considérée se
–ω t
2
posent, au moins pour t = 0.
u (x, t ) = b sinω x e ,
Ces deux doutes vont être levés l’un après l’autre par le principe
où b est une constante.
du maximum (§ 5.3).
On doit de plus avoir :
u (L, t ) = 0,
soit : 5.3 Principe du maximum
π
sinω L = 0 et ω = n ---- , où n ∈N∗ .
L
Nous allons montrer le théorème suivant.
On obtient donc des solutions à variables séparées (où bn est une
constante) :
Théorème 16 (principe du maximum pour l’équation de la
π  2 π2 
u (x, t ) = bn sin  n ---- x exp – n ------
- t . (33) chaleur ou principe de la casserole sans couvercle).
L  L 
2
Soit : T > 0 ;
Ω = ]0, π[ X ]0, ∞[ ; ΩT = ]0, π[ X ]0, T [ ;
À partir de maintenant, pour alléger les notations, nous sup-
poserons que L = π. ∂1ΩT la partie de la frontière de ΩT constituée des (x, t ) tels que
x = 0 ou π, ou t = 0.
Nos solutions (33) s’écrivent alors : Soit w ∈ C 2(Ω) ∩ C 0( Ω ), solution de l’inéquation de la chaleur
P (w ) > 0, où :
u (x, t ) = bn sinnx exp(–n2t )
2
∂ w ∂w
et vérifient les relations (30) et (32), mais n’ont aucune raison de P ( w ) = ----------
- – --------
∂x
2 ∂t
vérifier (31) ; mais, comme (32) est une équation linéaire, toute
combinaison linéaire finie : Alors :
N
nx n2t sup w ( m ) = sup w ( m ). (35)
∑ bn sin exp(– ) m ∈ ΩT m ∈ ∂1 ΩT
1

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
Le principe du maximum [relation (35)] entraîne donc :
w (x, T ) < 0,
∂1 ΩT ΩT ∂1 ΩT soit :
u (x, T ) < v (x, T ),
puis :
∂1ΩT
u (x, T ) = v (x, T )
puisque u et v jouent des rôles symétriques ; T étant arbitraire, on a
Figure 6 – Principe de la casserole sans couvercle
bien : u = v.
b) Supposons d’abord h de classe C 1 ; alors :
Intuitivement, la relation (35) dit que la fonction température w
atteint son maximum, dans la casserole ΩT (figure 6), au fond de ∞
cette casserole (t = 0) ou sur ses parois (x = 0 ou π). H ∈ C1 et ∑ bn ( H ) <∞
1
Preuve. ◊ Soit d’abord ε > 0 et wε = w + ε x 2, qui vérifie :
d’après le théorème 14.
P (wε ) = P (w ) + 2ε > 2ε > 0 ; 2
–n t
La série de fonctions continues bn (H ) sinnx e est donc norma-
soit m0 = (x0 , t0) un point du compact ΩT où wε atteint son maxi-
mum. lement convergente sur Ω et sa somme u (x, t ) définit une fonction
u ∈ C 0 (Ω ) ∩ C 2(Ω), vérifiant les relations (30), (32) et aussi (31) puis-
■ Si m0 ∉ ∂1ΩT, alors :
que, pour 0 < x < π :
a) 0 < x0 < π, donc :
∞
∂ wε
---------- ( m 0 ) = 0
∂x
u (x, 0) = ∑ bn ( H ) sinnx = H (x ) = h (x )
1
et : d’après le théorème 14.

2
∂ wε Cela prouve déjà au passage l’existence et l’unicité d’une solution
- ( m0 ) < 0
------------
∂x
2 u de l’équation de la chaleur quand h est de classe C 1, à savoir :
∞
b) 0 < t0 < T, donc : 2
∑ bn ( H ) sin nx e
–n t
u (x, t ) = (0 < x < π, t > 0) ;
1
∂w w ε ( x 0, t 0 – h ) – w ε ( x 0, t 0 )
---------ε- ( m 0 ) = lim -------------------------------------------------------------------
- >0.
∂t >
h→0
–h mais le principe du maximum (théorème 16) va permettre d’aller un
peu plus loin ; en effet, il nous donne :
Il en résulte que P (wε ) (m0) < 0, ce qui est une contradiction. Tt h (x ) = u (x, t ) < sup u < sup h ( x ) = h ∞,
∂1 Ωt x
■ Donc m0 ∈ ∂1ΩT et on obtient :

et de même :
sup w ( m ) < sup w ε ( m ) = sup w ε ( m ) < sup w ( m ) + ε π 2 , –Tt h (x ) < ||h ||∞ ,
m ∈ ΩT m ∈ ΩT m ∈ ∂1 ΩT m ∈ ∂1 ΩT
d’où b) quand h est C 1.
ce qui donne la relation (35) en faisant tendre ε vers 0. ◊
De plus, l’inégalité évidente :
Le théorème 16 donne immédiatement le résultat d’unicité sui-
vant. ∞ 2
||Tt h1 – Tt h2||∞ < ||h1 – h2||∞ ∑ e
–n t
Théorème 17 (théorème d’unicité pour l’équation de la montre que, pour t > 0 fixé, Tt h est une fonction continue de h.
chaleur)
a) Si u, v sont deux solutions des relations (30), (31) et (32), Les fonctions de classe C 1 étant denses dans E, b) est valable
alors u = v. pour toute fonction continue h. ◊
b) Pour t > 0, posons :
∞ 2
∑ bn ( H ) sin nx e
–n t
Tt h(x) = ; 5.4 Théorème d’existence et d’unicité
1
alors : ||Tt h ||∞ < ||h ||∞ (où || ||∞ désigne la norme sup dans La version quantitative b) du théorème d’unicité fournit presque
l’espace E des fonctions continues sur [0, π]). gratuitement le théorème suivant, qui résout complètement l’équa-
tion de la chaleur.
Preuve. ◊
Théorème 18 (théorème d’existence et d’unicité). Pour
a) Soit w = u – v et T > 0 ; P (w ) = 0 et w est nulle sur ∂1ΩT ; en toute donnée initiale h continue sur [0, π] (avec h (0) = h (π) = 0),
effet, u et v sont nulles sur les parois verticales de la casserole et : l’équation de la chaleur (relations (30), (31) et (32)) possède une
w (x, 0) = u (x, 0) – v (x, 0) = h (x ) – h (x ) = 0 solution et une seule.

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
Preuve. ◊ Posons : Soit b > 0 et y de classe C 1 à valeurs réelles sur [0, b], telle que :
∞
 2 y (0) = y (b ) = 0.
 u ( x, t ) = ∑ b n ( H ) sin nx e
–n t
si x ∈ [ 0, π ]et t > 0
 1 Alors :

Ey Ey
 u ( x, 0 ) = h ( x ) b b
b 2
Le seul point délicat est la continuité de u sur Ω , c’est-à-dire en 2
( t )d t <  --- ′ 2 ( t )d t . (37)
0  π 0
(x, 0) ; il va résulter, avec les notations du théorème 17, de la pro-
priété suivante :
Si, de plus, y est de classe C 2, on a aussi :
lim T t h – h ∞ = 0. (36)
Ey Ey
> b b
t→0 2
′ 2 ( t )d t <  ---
b
Soit, pour cela, ε > 0 et h0 de classe C 1 telle que ||h – h0||∞ < ε. ′′ 2 ( t )d t . (38)
0  π 0
D’après la preuve du théorème 17, on peut trouver δ > 0 tel que :
Preuve. ◊
||Tt h0 – h0 ||∞ < ε pour 0 < t < δ ;
pour un tel t, on a donc : ■ Supposons d’abord b = π. L’hypothèse permet de prolonger y
en une fonction impaire, 2π – périodique, C 1 sur R , avec donc
||Tt h – h ||∞ < ||Tt h – Tt h0 ||∞ + ||Tt h0 – h0 ||∞ + ||h0 – h ||∞ c0(y ) = 0.
< 2||h – h0 ||∞ + ||Tt h0 – h0 ||∞ < 3ε, L’identité de Parseval (§ 4.2) appliquée à y et y ’ donne alors :
Ey E
d’où la relation (36). π π ∞
1
y ( t )d t = π ∑ c k ( y ) ∑
2 2 2 2
La continuité de u en (x0 , 0) en résulte immédiatement ; en effet : ( t )d t = --- =π ck ( y )
0 2 –π k≠0
–∞
u (x, t ) – u (x0 , 0) = Tt h (x ) – h (x0) = Tt h (x ) – h (x ) + h (x ) – h (x0),
< π ∑ k c k ( y ) = π ∑ c k (y ′ )
2 2 2
d’où :
|u (x, t ) – u (x0 , 0)| < ||Tt h – h ||∞ + |h (x ) – h (x0)|.
E Ey
π π
1
u est donc solution de l’équation de la chaleur ; c’est la seule = --- y ′ 2 ( t )d t = ′ 2 ( t )d t .
2 –π 0
d’après le théorème 17 d’unicité ; les séries de Fourier ont joué un
rôle décisif, ce qui est un juste retour des choses... Si, de plus, y est de classe C 2 :
E
Exemple : h (x ) = x (π – x ) ; si bn = bn (H ), deux intégrations par π
parties donnent : 1 y ( π ) – y ( –π )
c 0 (y ′ ) = ------- y ′ ( t )d t = --------------------------------- = 0,
2π 2π
Et E E
π π π –π
π 1 1
--- b n = ( π – t ) sin nt d t = --- ( π – 2 t ) cos nt d t = -----2- 2 sin nt d t et le même calcul que ci-dessus montre que :
2 0 n 0 n 0
2 ( 1 – cos n π ) ∑ ck ( y ′ ) ∑ ck ( y ′′ )
2 2
-,
= ---------------------------------- < .
3
n
Cela prouve les relations (37) et (38) dans le cas particulier consi-
donc : déré.
8
b2k = 0 , b2k +1 = --- (2k + 1)–3,
π ■ Dans le cas général, posons :
et l’unique solution de l’équation de la chaleur avec donnée initiale h
est donnée par la formule :
z ( x ) = y  --- x
b
; z (0) = z (π) = 0,
∞ π
8
∑
–3
u (x, t ) = --- (2k + 1) sin((2k + 1)x) exp(– (2k + 1)2t ).
π
k=0 donc, le cas particulier précédent donne :
Ez Ez
Pour un barreau de longueur L et h (x ) = x (L – x ), on obtiendrait : π π
2
2 ∞ ( x )d x < ′ 2 ( x )d x ,
π  2 π 
2
( 2 k + 1 ) sin  ( 2 k + 1 ) --- x exp  – ( 2 k + 1 ) -----2-t .
8L
3 ∑
–3 0 0
u (x, t ) = --------- 
π k=0 L   L  soit encore :
Ey Ey
π π
2b b 2
--- x d x <  --- ′ 2  --- x d x ,
b
0 π   π 0 π 
ce qui donne la relation (37) par changement de variable ; la

6. Applications diverses relation (38) s’établit de même. ◊
des séries de Fourier Voici une application : considérons l’équation différentielle
linéaire à coefficients non constants :
y ’’ + py ’ + qy = 0,
6.1 Inégalité de Wirtinger
où p, q : R → C sont continues et telles que :
Il s’agit d’une inégalité reliant les normes L 2 d’une fonction et de
sa dérivée ; de façon précise, on a la proposition suivante. |p (x )| < M1 , |q (x )| < M2 ,
Proposition 4 (inégalité de Wirtinger). pour tout x réel.

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
On sait que les zéros d’une solution (non identiquement nulle) les nombres algébriques forment un sous-corps dénombrable Q de
sont isolés ; on va montrer plus quantitativement que l’écart mini- l’ensemble des réels.
mum b entre deux de ces zéros est assez grand, puisqu’il vérifie
l’inégalité :
2
Définition 2. La norme d’un réel x, notée ||x ||, est la distance
b b de x à l’entier le plus proche :
1 < M 1 --- + M 2 -----2- . (39)
π π ||x || = dist (x, Z ) = inf {|x – n | ; n ∈ Z }
On peut supposer :
y (0) = y (b) = 0, = min {|x – n | ; n ∈ Z }.
E
b 1⁄2
1
et on note ||f ||2 la quantité  f ( t ) d t
2
. On a toujours 0 < ||x || < --- ; par exemple, ||3/4|| = 1/4 et ||3,1416||
 0 2
= 0,1416. L’inégalité suivante se révèlera utile :
On a :
y ’’ = – py ’ – qy , 4||x || < |e2iπx – 1| < 2π||x ||. (39)
donc :
Écrivons, en effet :
|y ’’| < M1|y ’| + M2 |y |
et : x = n + r, où n ∈ Z et |r | = ||x || ;
||y ’’||2 < M1 ||y ’||2 + M2 ||y ||2 ; utilisant l’encadrement :
soit encore, en utilisant l’inégalité de Wirtinger : 2 π

--- |u | < |sinu | < |u | pour |u | < --- ,
π 2
 b b 
2
||y ’’||2 <  M 1 --- + M 2 -----2- ||y ’’||2 . nous obtenons :
 π π 
|e2iπx – 1| = 2|sinπr | > 4|r | = 4||x ||,
On peut simplifier par ||y ’’||2 > 0 pour obtenir la relation (39) ; car,
si on avait ||y ’’||2 = 0, y serait affine sur [0, b ], donc nulle sur [0, b ] et de même :
puisqu’elle s’annule en 0 et b ; et y serait identiquement nulle, |e2iπx – 1| < 2π||x ||.
contrairement à l’hypothèse.
Théorème 19 (théorème de Liouville). Si α est irrationnel
(39) admet la version légèrement améliorée suivante, due à algébrique de degré d (P (α ) = 0, P ∈ Z [X ], P de degré d mini-
Opial : mum), il existe une constante δ > 0 telle que :
2
b b ||qα || > δq 1 – d pour tout entier q > 1. (40)
1 < 2 M 1 -----2- + M 2 -----2- . (37bis)
π π
p
Preuve. ◊ Soit M = sup{|P ’(x )| ; |x – α | < 1} ; si --- est un rationnel :
q
P  --- = -----
p N
6.2 Une équation aux différences d
-≠0,
q q
Intéressons-nous à l’équation (rencontrée notamment en théorie
où N est un entier ; et donc : P  --- > -----
ergodique) : p 1
- ; distinguons maintenant
f (x + 2πα ) – f (x ) = g (x ) (38) q  d
deux cas. q
où g est une fonction donnée, 2π – périodique de moyenne nulle et p 1
de classe C ∞ ; α un nombre irrationnel fixé et l’inconnue f une fonc- Cas 1 : α – --- > -----d-
q q
tion continue 2π – périodique.
La solution de ce problème dépend étroitement de la nature p 1
« arithmétique » de α et nous allons le résoudre dans un cas particu- Cas 2 : α – --- < -----d- ( < 1).
q q
lier en utilisant les séries de Fourier ; il nous faut d’abord deux défi-
nitions et un théorème. Alors, le théorème des accroissements finis et la remarque initiale
Définition 1. α est dit algébrique s’il existe un polynôme à 1à savoir P  p--q- > q-----1- 2 donnent :
d
coefficients entiers :
d
∑ ak X - < P  --- = P ( α ) – P  --- < M α – --- .

P(X) =
k
, 1 p p p
-----
d q  q  q
0 q
avec d > 1 et ad ≠ 0, tel que P (α ) = 0.

La relation (40) s’ensuit avec δ = min  1, ----- . ◊
1
 M
1 1+ 5
Ainsi, α = 2 , α = ------- , le nombre d’or α = ----------------- sont algébri-
3
Théorème 20. Soit α un irrationnel algébrique ; alors
2 2
l’équation aux différences (38) possède une solution f continue
ques puisqu’ils vérifient respectivement : et 2π – périodique et, de plus, f est de classe C ∞.
α 3 – 2 = 0 ; 2α 2 – 1 = 0 ; α 2 – α – 1 = 0 ; Deux solutions de (38) diffèrent d’une constante.

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
Preuve. ◊ Supposons le problème résolu, et prenons les coeffi- H. Weyl a remarqué qu’on peut écrire la relation (42) sous la
cients de Fourier des deux membres de la relation (38) en utilisant la forme :
E
proposition 2 pour obtenir : N 1
1
(e2in πα – 1)cn(f ) = cn(g ). ----
N ∑ 1I ( { xn } ) → 1 ( t )d t
0 I
(42bis)
n=1
Si n ≠ 0, e2iπnα – 1 ≠ 0 puisque α est irrationnel, et cn (f ) est parfai- où 1I est la fonction indicatrice de I et où le premier membre de
tement déterminé (rappelons que c0(g ) = 0) : (42bis) rappelle une somme de Riemann.
cn ( g ) Cette forme plus fonctionnelle de l’équirépartition l’a conduit au
c n (f ) = -------------------------
-.
e
2iπ nα
–1 résultat suivant, dont la preuve utilise les séries de Fourier.
D’après le théorème d’unicité (théorème 2), f – c0(f ) est entière-

ment déterminée ; on ne peut rien dire de plus puisqu’il est clair que Théorème 21 (critère de Weyl). Soit ω = ( x n ) n >1 une suite
si f est solution de (38) et c une constante, f + c est encore solution de réels ; on a équivalence entre :
de (38). Cela règle le problème de l’unicité modulo les constantes a) ω est équirépartie modulo 1 ;
dans le théorème 20. Il reste le problème de l’existence ; posons
Ef t
N 1
pour le résoudre : 1
cn ( g )
b) ----
N ∑ f ( { xn } ) →
0
( )d t
f ( x ) = ∑ -------------------------
i nx
2iπ nα
-e . (41) n=1
n≠0 e –1 pour toute fonction f Riemann-intégrable sur [0, 1] ;
N
1
∑
La série au second membre de (41) est normalement 2iπ hx n
c) ---- e → 0 pour tout entier h ≠ 0.
convergente ; en effet, d’après les relations (39) et (40), on a la N
n=1
minoration :
|e2iπnα – 1| > 4|| |n |α || > 4δ|n |1–d, Nous allons admettre ce théorème [2], mais nous en servir pour
d’où : donner un exemple de suite équirépartie modulo 1 et une applica-
tion aux séries entières et au développement en base 10.
cn ( g ) 1
- |n|d – 1|cn(g)| = εn .
- < -----
-------------------------
2iπ nα 4δ Proposition 5.
e –1
∞
Soit α un nombre irrationnel.
La série ∑ εn est convergente d’après la proposition 2 et le théo- a) La suite ω = ( nα ) n >1 est équirépartie modulo 1.
–∞
rème 14 ; en effet : ∞
∑
n
|n |d –1|cn(g )| = |cn(g (d –1))| b) La série entière A ( z ) = { nα } z n’a sa somme bornée au
n=1
et g est de classe C d, donc g (d –1) est de classe C 1 ; f est donc parfai- voisinage d’aucun point du cercle de convergence Γ = {z ; |z | = 1} ;
cn ( g ) en particulier, Γ est une coupure pour la série entière.
tement déterminée et : c n (f ) = -------------------------
- pour n ≠ 0, d’après le
e
2iπ nα
–1 Preuve. ◊
théorème 3. a) Utilisons le c) du critère de Weyl, en remarquant que e2iπhα ≠ 1
Remontant les calculs (on peut aussi procéder directement à par- puisque α est irrationnel ; on a :
tir de (41)), on voit que les fonctions f (x + 2πα ) – f (x ) et g (x ) ont N 2iπ hα 2iπ hNα
1 e 1–e
∑
2iπ hnα
même transformée de Fourier, donc sont égales d’après le théorème ε N = ---- e = ---------------- -----------------------------
2iπ hα
,
d’unicité ; enfin, il est clair que (41) peut être dérivée terme à terme N N 1–e
n=1
autant de fois qu’on veut, puisque : et :
2
ε N < ----------------------------------
-,
∑n
k
|cn(g)| < ∞ pour tout k ∈N ; N1–e
2iπ hα
f est donc C ∞ et la démonstration est achevée. ◊ ce qui donne le résultat.

b) Démontrons la propriété préliminaire suivante :
c1 + … + cN ∞
------------------------------- → c ⇒ lim ( 1 – r ) ∑ c n r = c .
n
6.3 Critère de Weyl. Loi de Benford N <
(43)
r→1 1
Définition 3. Si x ∈ R, [x] désigne la partie entière de x et : Posons en effet :

∞
∑ cn r
n
{x} = x – [x] C(r) = .
1
s’appelle sa partie fractionnaire ; 0 < {x } < 1. <
On a notoirement, quand r → 1 :
∞ ∞
C (r ) = (1 – r ) ∑ ( c 1 + … + c N ) r = (1 – r ) ∑ ( Nc + s ( N ) ) r
N N
Définition 4. Une suite ω = ( x n ) n >1 de réels est dite équiré- 1 1

partie modulo 1, si on a : ∞ ∞
= c (1 – r ) ∑ N rN + (1 – r ) ∑ s ( N ) r N
A ( I, N, ω )
lim -------------------------- = I (42) 1 1
N→∞ N
s  -------------------
r 1–r
= c (1 – r ) ------------------2- +
pour tout intervalle semi-ouvert à droite I = [a, b [ de [0, 1[, où  2
(1 – r) (1 – r)
|I| = b – a est la longueur de I et A (I, N, ω) le nombre d’indices
= ----------- + s  ----------- ,
cr 1
n < N tels que la partie fractionnaire {xn } de xn appartienne à I.
1–r 1 – r 

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
donc : (1 – r )C (r ) → c . premier chiffre en base 10 qui apparaît dans 2n ; les premières

valeurs de n donnent le tableau ci-après :Au vu de ce tableau, où 8
apparaît cinq fois comme premier chiffre dans les quarante-trois
Considérons maintenant A (r e2ik πα ), où k est un entier non nul : premières puissances de 2, alors que 7 n’apparaît comme tel que
∞ N dans la quarante-sixième puissance de 2 (et 9 encore plus tard), on
A (r e2ik πα ) = ∑ { nα } e2ik πnαr n = ∑ f ( { xn } ) r n pourrait penser que la proportion de 8 est plus forte que celle de 7 ;
n=1 n=1 on va voir qu’il n’en est rien, et qu’on a le résultat suivant.
où : f (t ) = t e2iπkt et xn = nα ;
d’après le b) du critère de Weyl : Théorème 22 (loi de Benford). Soit k ∈ {1, 2, ..., 9} ; alors
Et
N 1 la fréquence asymptotique Fk du nombre de puissances de 2
1 1
∑
2iπ kt commençant par le chiffre k en base 10 est :
---- f ( { xn } ) → e d t = ------------ = c ≠ 0 ;
N 0 2i k π
n=1
F k = log 10  1 + --- = lg  1 + ---
1 1
d’après (43) : (44)
k k
(1 – r )A (r e2ik πα ) → c ≠ 0 ; En particulier, Fk décroît avec k et F8 < F7 .

<
en particulier, A (r e2ik πα ) n’est pas bornée quand r → 1 . Les points
de la forme e2ik πα étant denses dans Γ, A n’est bornée au voisinage Preuve. ◊ Soit EN (k ) l’ensemble des n < N tels que 2n com-
d’aucun point de Γ. ◊ mence par k en base 10 ; il s’agit de montrer que :
lim ---- E N ( k ) = lg  1 + --- .

Considérons maintenant le développement en base 10 des puis- 1 1
(45)
sances successives de 2 et intéressons-nous particulièrement au N→∞ N  k
n 2n n 2n
2 4 28 2 6 8 4 3 5 4 3 6
3 ➇ 29 5 3 6 8 7 0 9 1 2
4 1 6 30 1 0 7 3 7 4 1 8 2 4
5 3 2 31 2 1 4 7 4 8 3 6 4 8
6 6 4 32 4 2 9 4 9 6 7 2 9 6
7 1 2 8 33 ➇ 5 8 9 9 3 4 5 9 2
8 2 5 6 34 1 7 1 7 9 8 6 9 1 8 4
9 5 1 2 35 3 4 3 5 9 7 3 8 3 6 8
10 1 0 2 4 36 6 8 7 1 9 4 7 6 7 3 6
11 2 0 4 8 37 1 3 7 4 3 8 9 5 3 4 7 2
12 4 0 9 6 38 2 7 4 8 7 7 9 0 6 9 4 4
13 ➇ 1 9 2 39 5 4 9 7 5 5 8 1 3 8 8 8
14 1 6 3 8 4 40 1 0 9 9 5 1 1 6 2 7 7 7 6
15 3 2 7 6 8 41 2 1 9 9 0 2 3 2 5 5 5 5 2
16 6 5 5 3 6 42 4 3 9 8 0 4 6 5 1 1 1 0 4
17 1 3 1 0 7 2 43 ➇ 7 9 6 0 9 3 0 2 2 2 0 8
18 2 6 2 1 4 4 44 1 7 5 9 2 1 8 6 0 4 4 4 1 6
19 5 2 4 2 8 8 45 3 5 1 8 4 3 7 2 0 8 8 8 3 2
20 1 0 4 8 5 7 6 46 ➆ 0 3 6 8 7 4 4 1 7 7 6 6 4
21 2 0 9 7 1 5 2 47 1 4 0 7 3 7 4 8 8 3 5 5 3 2 8
22 4 1 9 4 3 0 4 48 2 8 1 4 7 4 9 7 6 7 1 0 6 5 6
23 ➇ 3 8 8 6 0 8 49 5 6 2 9 4 9 9 5 3 4 2 1 3 1 2
24 1 6 7 7 7 2 1 6 50 1 1 2 5 8 9 9 9 0 6 8 4 2 6 2 4
25 3 3 5 5 4 4 3 2 51 2 2 5 1 7 9 9 8 1 3 3 6 8 2 4 8
26 6 7 1 0 8 8 6 4 52 4 5 0 3 5 9 9 6 2 7 3 7 0 4 9 6
27 1 3 4 2 1 7 7 2 8 53 ➈ 0 0 7 1 9 9 2 5 4 7 4 0 9 9 2

DOCUMENTATION
19/09/2008
DOCUMENTATION
19/09/2008
, ,
Or, n ∈ EN (k ) ⇔ n < N et k · 10 < 2 n < (k + 1) 10 pour un , ∈ N. et :
{nα } ∈ [lg k, lg (k + 1)[ = I.
log 2
Posons provisoirement α = ---------------- = lg2 ; α est irrationnel et : D’après le critère de Weyl appliqué à l’irrationnel α :
log 10
EN ( k )
n ∈ EN (k ) ⇔ n < N lim --------------
- existe et vaut |I|, autrement dit F existe et vaut
N→∞
N k
et : 1
lg(k + 1) – lg k = lg (1 + --- ). ◊
lg k + , < nα < lg (k + 1) + , ⇔ n < N k
Références bibliographiques
[1] DAVIS (P.). – Interpolation and approximation. [3] ZYGMUND (A.). – Trigonometric Series, [4] ARNAUDIES (J.M.) et FRAYSSE (H.). – Cours
[2] KUIPERS (L.) et NIEDERREITER (H.). – Uni- Second Edition. Cambridge University Press, de mathématiques, tome 3. Dunod.
form distribution of sequences. Wiley-Inters- 1959.
cience Series, 1974.

DOCUMENTATION
19/09/2008

Af 141

Transféré par

Informations du document

Titre original

Copyright

Formats disponibles

Partager ce document

Partager ou intégrer le document

Options de partage

Avez-vous trouvé ce document utile ?

Ce contenu est-il inapproprié ?

Droits d'auteur :

Formats disponibles

Af 141

Transféré par

Droits d'auteur :

Formats disponibles

Dossier délivré pour

par Hervé QUEFFÉLEC

1. Coefficients de Fourier d’une fonction 2π – périodique ................ AF 141 - 3

appelons qu’une fonction f : R → C est dite T – périodique si,

Dossier délivré pour

— la première opération s’appelle l’analyse de f ;

Ces deux opérations sont inverses l’une de l’autre, comme la dérivation et

Considérons l’exemple du noyau de Poisson Pr , donné par la formule :

L’analyse de Pr , 2 π – périodique, conduit à montrer qu’il se représente par la

et on retrouve la relation (A).

ce qui est peu clair sous la forme (A).

Dossier délivré pour

Il sera commode d’introduire également l’espace C k (k > 0) des

2π – périodique ||f ||∞ = sup {|f (t )| ; t ∈R} pour f ∈ C 0

E les coefficients de Fourier an (f ), bn (f ), cn (f ) par les formules :

— la classe 5 des fonctions 2π – périodiques Riemann – = ... + ... + ...

Dossier délivré pour

1.3 Convolution de deux fonctions

où M est une constante numérique.

E fx d’où fˆ = 1 et ^ est de norme 1.

Dossier délivré pour

N ( t )d t → 0 quand N → ∞. (11) Or, on démontre (continuité de la translation dans L 1) que g ∈ C 0 ;

Soit, en effet ε > 0, M = ||g ||∞ et δ ∈]0, π[ tel que :

∑ ck < ∞ à l’aide du critère de Cauchy de convergence uniforme.

KN est de la forme : Théorème 3.

Dossier délivré pour

Preuve. ◊ (série de Bertrand divergente) et donc qu’une série trigonométrique

Exemple 2Soit : ∞ < |n|–k ab k k kα ;

où C est une constante numérique.

Dossier délivré pour

où rN (t ) est une quantité uniformément bornée. Enfin, un change-

existent (f possède une limite à droite et une limite à gauche en x0) ;

c) D’après le théorème 1 : existent (f est en un certain sens dérivable à droite et dérivable à

Corollaire 1. Schéma de preuve. ◊ On peut supposer x0 = 0. Le théorème 4

Dossier délivré pour

Soit a ∈ C\ Z et f la fonction de L 1 définie par :

f (t ) = eiat si – π < t < π ; x0 = π.

au voisinage d’un point x0 ne dépend que du comportement de f au puis :

Théorème 8 (théorème de Dirichlet local). Soit f ∈ L 1, de

Dossier délivré pour

Le théorème de convergence non tangentielle d’Abel [4] entraîne la

avec f ( t ) = exp – icot --- si 0 < t < 2π ; f (0) = 0.

C’est une vérification facile ; mais la proposition 3 se révèle utile

Dossier délivré pour

3.2 Fonction signal. Fonction triangle Autrement dit, on a :

Le théorème de Dirichlet ponctuel (théorème 5) s’applique en N

convolution est paire, nulle sur [2ε, π]. 2 ∑ -----------------------2-

en faisant le changement de variable t = π – u dans la seconde

Dossier délivré pour

■ Considérons maintenant la fonction F définie sur [–1, 1] = I par 2 1 2

qui suivent la formule :

■ Posons EN = inf{||F – P ||∞ }, où ∞ = sup et où P parcourt les

Dossier délivré pour

cn (f ) = (f/en ) pour f ∈ L 2. (26)

4.2 Inégalité de Bessel. Exemple 2Changeons a en ia (a > 0) dans l’exponentielle

–∞ et l’équation (29) se lit :

On voit donc que l’appartenance d’une fonction à L 2 se lit entière-

Dossier délivré pour

et on retrouve la célèbre relation : Théorème 15. Si f ∈ L 2 et N > 0, SN (f ) est la meilleure

4.3 Fonctions de classe C 1

Dossier délivré pour

et u ∈ C 2(Ω ) ∩ C 0 (Ω ) . vérifie aussi (30) et (32) et le principe est de considérer des

u (x, t ) = f (x ) g (t ) la relation (31) donne :