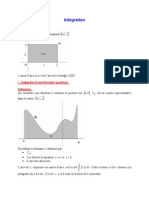
Calcul intégral Cours

CHAPITRE 16 : CALCUL INTEGRAL

La notion d’intégrale a été définie au chapitre 9.

Rappelons que l’on a toujours a ≤ b

1. Propriétés de l’intégrale

1.1. Relation de Chasles

Soit f continue sur I, trois réels a, b et c quelconques de l’intervalle I,

b c b

∫ a
f ( x) dx = ∫ f ( x) dx + ∫ f ( x) dx
a c

Démonstration admise (dans le cas général, on peut facilement la démontrer lorsque f est positive
sur I )

Exemple
2π

Calculer ∫ 0
sin x dx

On utilise la relation de Chasles

2π π 2π π 2π

∫ sin x dx = ∫ sin x dx + ∫ (− sin x )dx = [ − cos x ] + [ cos x ] = 4

0 0 π 0 π

© Gérard Hirsch – Maths54 1

 Calcul intégral Cours

1.2. Linéarité

1.2.1. Intégrale et addition des fonctions

Propriété
b b b

∫ a
( f ( x) + g ( x))dx = ∫ f ( x) dx + ∫ g ( x) dx
a a

Démonstration
En effet, si F et G désignent une primitive sur I de f et g respectivement, alors
b

( f ( x) + g ( x))dx = [ F ( x) + G ( x) ] = [ F (b) + G (b) ] − [ F (a) + G (a) ] =

b

∫ a a

b b

[ F (b) − F (a)] + [G (b) − G (a)] = ∫ a

f ( x) dx + ∫ g ( x) dx
a

1.2.2. Intégrale et constante multiplicative

Propriété
b b

∀k ∈ R , ∫ a
k f ( x) dx = k ∫ a
f ( x) dx

Démonstration
Si F désigne une primitive de f, alors
b b

k f ( x) dx = [ kF ( x) ] = k [ F (b) ] − k [ F (a )] = k [ F (b) − F (a) ] = k ∫ f ( x) dx

b

∀k ∈ R , ∫ a a a

Remarque
En appliquant les deux propriétés précédentes, on obtient ;
Si f1 et f 2 sont des fonctions continues sur [ a , b ] , alors
b b b

∀k1 ∈ R , ∀k2 ∈ R , ∫ [ k1 f1 ( x) + k2
a
f 2 ( x) ] dx = k1 ∫ a
f1 ( x) dx + k2 ∫ f 2 ( x) dx
a

© Gérard Hirsch – Maths54 2

 Calcul intégral Cours

1.2.3. Interversion des bornes

Propriété
a b

∫ b
f ( x) dx = − ∫ f ( x) dx
a

Démonstration
a b

∫ b
f ( x) dx = F (a ) − F (b) et ∫ a
f ( x) dx = F (b) − F (a )

1.3. Ordre et intégration

Propriété
b

i). si ∀x ∈ [ a , b ] , f ( x) ≥ 0 alors ∫ f ( x) dx ≥ 0
a

ii). si ∀x ∈ [ a , b ] , f ( x) ≤ 0 alors ∫ f ( x ) dx ≤ 0
a

b b

iii). si ∀x ∈ [ a , b ] , f ( x) ≤ g ( x) alors ∫ f ( x) dx ≤ ∫ g ( x) dx
a a

Démonstration
b

i) ∫ a
f ( x) dx représente une aire, qui par définition est un réel positif

ii) ∫ a
f ( x) dx est égale à l’opposé de l’aire

iii) si ∀x ∈ [ a , b ] , f ( x) ≤ g ( x) alors f ( x ) − g ( x) ≤ 0
b

et d’après ii) ∫ [ f ( x) − g ( x)] dx ≤ 0 , soit en appliquant la linéarité de l’intégrale 1.2

a

b b

alors ∫ a
f ( x) dx ≤ ∫ g ( x) dx
a

© Gérard Hirsch – Maths54 3

 Calcul intégral Cours

1.4. Valeur moyenne d'une fonction et inégalité de la moyenne.

1.4.1. Valeur moyenne d’une fonction

Définition
f une fonction continue sur un intervalle I, on appelle valeur moyenne de f sur [ a , b ]

1 b
b − a ∫a
le nombre réel égal à f ( x) dx

Exemple
 π
Calculer la valeur moyenne de la fonction f : x a cos x sur  0, 
 2
π/2 π/ 2
Nous avons ∫ cos x dx = [sin x ] =1
0 0

 π 1 2
La valeur moyenne de la fonction f : x a cos x sur  0,  est égale à =
 2 π π
2

1.4.2. Inégalité de la moyenne

Théorème
Soit f est une fonction continue sur un intervalle I et a et b deux réels ∈ I
i) Si ∀x ∈ I , il existe deux réels m et M avec m ≤ f ( x) ≤ M alors
b

m(b − a) ≤ ∫ f ( x) dx ≤ M (b − a )
a

ii) Si ∀x ∈ I , il existe un réel M > 0 avec f ( x) ≤ M

b

∫ a
f ( x) dx ≤ M (b − a)

© Gérard Hirsch – Maths54 4

 Calcul intégral Cours

Démonstration
Si ∀x ∈ I , il existe deux réels m et M avec m ≤ f ( x) ≤ M , en intégrant entre a et b, puisqu’il y a
conservation de l’ordre, on obtient :
b b b

∫ a
m dx ≤ ∫ f ( x) dx ≤ ∫ M dx
a a

b b

Puisque ∫ a
m dx = (b − a )m et ∫ a
M dx = M (b − a )

On a bien m(b − a ) ≤ ∫ f ( x) dx ≤ M (b − a )
a

Exemple
1 1

Comparer les deux intégrales I = ∫ x 2 dx et J =∫ 1 + x 4 dx

0 0

On a ∀x ∈ R, x 4 < 1 + x 4

la fonction ϕ : X a X est strictement croissante sur [ 0 , + ∞[

et donc, en particulier ∀x ∈ [ 0 , 1 ] , x 2 < 1 + x 4

1 1

et I = ∫ x 2 dx < J = ∫ 1 + x 4 dx
0 0

1.5. Intégrales de fonctions paires, impaires, périodiques

Propriété
a a

i) Si f est une fonction paire et si f est continue sur [ − a , a ] alors ∫ f ( x) dx = 2 ∫ f ( x) dx

−a 0

ii) Si f est une fonction impaire et si f est continue sur [ − a , a ] alors ∫ f ( x) dx = 0

−a

iii) Si f est continue sur R et de période T alors quel que soit le nombre réel α
α+T T

∫ α
f ( x) dx = ∫
0
f ( x) dx

© Gérard Hirsch – Maths54 5

 Calcul intégral Cours

Exemple
π
x
Calculer ∫ −π
sin sin 2 x dx
3
x
La fonction f : x a sin sin 2 x est continue sur [ −π , π] et impaire
3
π
x
Donc ∫ −π
sin sin 2 x dx = 0
3
π/4

De même ∫ −π/ 4
tan x dx = 0 (continuité et imparité )

 π π
La fonction f : x a tan x est continue sur  − ,  et impaire
 4 4

Exemple
1

∫
3
Calculer x dx
−1

est continue sur [ −1, 1 ] et paire

3
La fonction f : x a x
1
1 1
 x4  1
∫ dx = 2∫
3
x x dx = 2   =
3
−1 0
 4 0 2

Exemple
2π
sin x
Calculer l’intégrale I = ∫ dx
0 2 + cos x sin 2 x
sin x
La fonction f : x a est continue sur R , donc I existe
2 + cos x sin 2 x
Puisque ∀x ∈ R, f ( x + 2π) = f ( x) , la fonction f est de période T = 2π
En appliquant la propriété iii) avec α = −π
2π
sin x π
sin x
on a ∫
0 2 + cos x sin x
2
dx = ∫
− π 2 + cos x sin
2
x
dx

© Gérard Hirsch – Maths54 6

 Calcul intégral Cours

La fonction f est aussi impaire et son intégrale sur [ − π , π ] est nulle

2π
sin x
donc I = ∫ dx = 0
0 2 + cos x sin 2 x

2. Lien entre intégrale et primitive

Théorème
f une fonction continue sur un intervalle I et a ∈ I
x

La fonction F définie sur I par : F ( x) = ∫ f (t ) dt est l’unique primitive sur I de la fonction f qui
a

s’annule sur I.

Application
1
1) Montrer que, pour tout t ≥ 0 , 1− t ≤ ≤ 1− t + t2
1+ t
x2 x 2 x3
2) En déduire que pour x ≥ 0, x− ≤ ln(1 + x) ≤ x − +
2 2 3
On étudie le signe des différences
1 1 − (1 − t 2 ) t2
− (1 + t ) = = qui est un nombre positif lorsque t ≥ 0
1+ t 1+ t 1+ t
1
Donc ∀t > 0, 1− t ≤
1+ t
De même
1 (1 − t + t 2 )(1 + t ) − 1 t 3
1− t + t2 − = = qui est un nombre positif lorsque t ≥ 0
1+ t 1+ t 1+ t
1
Donc ∀t > 0, ≤ 1− t + t2
1+ t
x

Utilisons le théorème : la fonction F définie sur I = [ 0, x ] par : F ( x) = ∫ f (t ) dt est l’unique

0

primitive sur [ 0 , x ] de la fonction f qui s’annule en 0.

© Gérard Hirsch – Maths54 7

 Calcul intégral Cours

Si x ≥ 0 , les inégalités précédentes sont valables sur [ 0, x ] , et donc

x x
dt x

∫0
(1 − t ) dt ≤ ∫
0 1+ t
≤ ∫ (1 − t + t 2 ) dt
0

soit
x2 x 2 x3
∀x ≥ 0, x− ≤ ln(1 + x) ≤ x − +
2 2 3

Application
x
dt
F est la fonction définie sur R par F ( x) = ∫
0 1+ t2
Déterminer le sens de variation de F sur R
1
La fonction f : t a est continue sur R , donc F existe et F est l’unique primitive de f qui
1+ t2
s’annule pour x = 0 .

 x dt ′ 1
F est dérivable sur R et ∀x ∈ R , F '( x) =  ∫ 2 
=
 0 1+ t  1+ x
2

donc ∀x ∈ R , F '( x) > 0

Fest strictement croissante sur R

3. Calcul de volume

r r r
L’espace est muni d’un repère orthonormé ( O ; i , j , k )
L’unité de volume est le volume du cube ayant pour arête l’unité de longueur définie par le
repère

Théorème
On considère un solide délimité par les plans d’équations respectives z = a et z = b .
On désigne par B( z ) la section plane de ce solide avec le plan perpendiculaire à Oz de cote z
( a ≤ z ≤ b)

© Gérard Hirsch – Maths54 8

 Calcul intégral Cours

On note S ( z ) l’aire de la section B( z )

Le volume V, en unités de volume, de ce solide est égal à :
b

V = ∫ S ( z ) dz
a

Exemple
Volume d’une sphère
Considérons la sphère de centre O et de rayon R.
Elle est située entre les plans de cotes -R et R
Soit z un réel de [ − R , R ] . L’intersection de la sphère et du plan de cote z est le disque B( z ) de

rayon r = R 2 − z 2 dont l’aire est égale à S ( z ) = π r 2 = π( R 2 − z 2 )

La fonction f : z a S ( z ) est une fonction continue sur [ − R , R ]

Le volume de la sphère est donc égal à :

R
R R
 z3   2R3 2R3  4 3
V = ∫ S ( z ) dz = ∫ π( R − z ) dz = π  R 2 z −  = π 
2 2
−( ) = πR
−R −R
 3 −R  3 3  3

© Gérard Hirsch – Maths54 9