Académique Documents
Professionnel Documents
Culture Documents
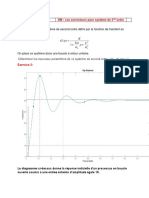
SMV CH 2 Séance Du 21 Octobre 2020
Transféré par
SALIM BOUAZIZITitre original
Copyright
Formats disponibles
Partager ce document
Partager ou intégrer le document
Avez-vous trouvé ce document utile ?
Ce contenu est-il inapproprié ?
Signaler ce documentDroits d'auteur :
Formats disponibles
SMV CH 2 Séance Du 21 Octobre 2020
Transféré par
SALIM BOUAZIZIDroits d'auteur :
Formats disponibles
Cours de systèmes multivariables
Chapitre 2 : Commandabilité, Observabilité et Formes standards
I. Introduction
Un système multivariable est décrit, dans l'espace d'état, par la représentation d'état suivante :
X(t) = A X(t) + B u(t)
(II.1)
y(t) = C X(t) + D u(t)
où : X(t) n est le vecteur d'état, u m est le vecteur des entrées et y l est le
vecteur des sorties ; les matrices A, B, C et D sont de dimensions convenables. Celui-ci peut
être caractérisé par une matrice fonction de transfert G(p) irréductible.
La question qui se pose est comment connaitre, sans calculer G(p), que l'ordre de la
représentation d'état est minimal ?
Pour répondre et comme on a vu dans le cours de régulation industrielle, deux propriétés sont
à considérer : les notions de commandabilité et d'observabilité.
II. Commandabilité
Contrairement au cas monovariable, deux types de commandabilité sont à étudier dans le cas
multivariable : la commandabilité d'état et celle de sortie.
II.1. Commandabilité d'état
La définition est similaire à celle du système monovariable : "Il existe une commande u(t), sur
un intervalle [t0 , t1], qui permet de ramener le vecteur d'état X(t) d'un état initial X(t0) à un
état final X(t1) arbitraires.
Théorème : Le système, décrit par (II.1), est commandable d'état, ou commandable tout
cours, si et seulement si la matrice C, dite de commandabilité, donnée par l'expression :
C = [B, AB, A2B, ... , An-1B], est de rang égal à n.
Exemple : Soit un système, d'ordre 2, décrit par les matrices A et B suivantes :
0 1 1 1
A= et B = = [b1 b2].
1 0 1 −1
- Commandabilité par rapport aux deux entrées :
1 1 1 −1
On a : C = [B, AB] = ; elle est de rang égal à 2 ; ce qui fait que le système
1 −1 1 1
est commandable d'état par rapport aux deux entrées.
Il est à signaler, dans le cas multivariable, qu'il n'est pas toujours nécessaire de calculer tous
les éléments de la matrice de commandabilité. Par exemple, dans cette application, on a un
nombre d'entrée égal à l'ordre du système, ce qui fait que la matrice B est carrée. Si son
déterminant est non nul, et c'est le cas, alors le système est bien commandable d'état.
Chapitre 2 -1- M. GASMI
Cours de systèmes multivariables
- Commandabilité par rapport aux entrées isolées :
1 1
– Pour l'entrée u1, on a : C1 = [b1 Ab1] = , de rang 1. Donc le système n'est pas
1 1
commandable par rapport à la première entrée isolée.
1 −1
– Pour l'entrée u2, on a : C2 = [b2 Ab2] = , de rang 1 aussi. Donc le système
−1 1
n'est pas commandable par rapport à la deuxième entrée isolée.
On peut montrer que lorsque le système est commandable d'état par rapport à toutes les
entrées, il peut être commandable par rapport à une seule entrée combinaison linéaires de
celles-ci.
1
Pour l'exemple, si on choisit une entrée u' telle que : u' = [u1 + u 2 ] , on obtient une matrice
2
1 1 1 0
de commande b donnée par : [b1 + b2 ] = . On a alors : C' = [b Ab] = , de rang
2 0 0 1
égal à 2. Le système est donc commandable par rapport à l'entrée u'.
II.2. Commandabilité de sortie
Définition : Un système multivariable est dit commandable de sortie, ou commandable
fonctionnel ou commandable f, si pour un vecteur de sortie y, il existe un vecteur de
commande, définis pout t > 0, qui permet de générer y à partir des conditions initiales.
Théorème : Pour un système décrit par la représentation d'état II.1, on a :
– si : l = m, le système est commandable de sortie si le déterminant de G(p) est non nul,
– si : l < m, le système est commandable de sortie s'il existe au moins un mineur de G(p),
d'ordre (l x l), non nul,
– si : l > m, le système est non commandable de sortie.
Remarques :
– Lorsqu'on parle de commandabilité tout cours, on veut dire commandabilité d'état.
– La commandabilité d'état n'implique pas la commandabilité de sortie et vice-versa.
1 1
p p + 1
Exemple 1 : Soit un système décrit par : G(p) = .
1 1
p + 2 p
1 1
On a : m = l = 2 et |G(p)| = − 0 le système est commandable f.
2 (p + 1)(p + 2)
p
1 1 1
p p p + 1
Exemple 2 : Pour le système décrit par : G(p) = , on a : m = 3 et l = 2
1 1 1
p + 2 p+2 p
donc : l < m. On a trois mineurs :
Chapitre 2 -2- M. GASMI
Cours de systèmes multivariables
1 1 1 1
p p p p +1
|G1(p)| = = 0 et |G2(p)| = |G3(p)| = 0
1 1 1 1
p+2 p+2 p+2 p
le système est donc commandable f.
T
1 1 1
p p p + 1
Exemple 3 : Pour le système décrit par : G(p) = , on a : m = 2 et l = 3
1 1 1
p + 2 p+2 p
donc : l > m le système est non commandable f.
II.3. Observabilité
La définition est similaire à celle du cas monovariable : En suivant la sortie et l'entrée sur un
intervalle donné, on peut déterminer l'état initial X(0).
Théorème : Le système multivariable, décrit par II.1, est observable si et seulement si le
rang de la matrice observabilité O, donnée par :
C
CA
O = C A CT AT CT A 2T CT
2
A(n −1)T CT ,
n −1
C A
est égal à l'ordre n du système.
Exemple : Soit un système décrit par le triplet matriciel suivant :
0 1 1 2 1 1
A= , B = −3 −4 et C = −2 −2 .
−3 −4
Il est simple de voir que les valeurs propres de A sont : (–1) et (–2) ; la matrice observabilité
1 −2 −3 6
correspondante est donnée par : O = CT ATCT =
1 −2 −3 6
Elle est de rang 1 ce qui fait que le système est non observable.
1 −2 −2
p + 2 4 4
La matrice fonction de transfert correspondante est telle que : G(p) = . Il est
simple de constater qu'elle possède un seul pôle égal à (– 2). Ce qui montre que le pôle (– 1) a
été simplifié, d'où la non observabilité du système.
Remarques :
– Comme il a été déjà vu dans le cours de Régulation industrielle, l'ordre d'un système est
celui de la matrice fonction de transfert irréductible ce qui correspond à l'ordre d'une
représentation d'état conduisant à un système commandable et observable.
– Toutes les définitions et théorèmes relatives au cas continu restent valables pour le cas
discret ; il suffit de remplacer p par z et la dérivée X' par X(k+1).
Chapitre 2 -3- M. GASMI
Cours de systèmes multivariables
III. Formes standards
III.1. Cas de la représentation d'état
III.1.1. Forme canonique de commandabilité
Pour le système décrit par (II.1) supposé commandable, on calcule la matrice de passage T à
la forme canonique de commandabilité. Pour cela, on forme d'abord la matrice
commandabilité c suivante : c = B AB A 2B A n −1B
Les vecteurs sont étalés comme suit :
n −1 n −1
c = b1 b 2 b m A b1
2
A b m A b1
2
A bm A b1 A bm
B AB A2B An–1B
Algorithme à suivre :
(i) Inspecter les colonnes de la gauche vers la droite et tirer les n premiers vecteurs
linéairement indépendantes.
(ii) Arranger ceux-ci pour former la matrice suivante :
= b1 A b1 A1 −1 b1 b 2 A b2 A 2 −1 b2 bm A m −1 b m
Les coefficients i, ou encore max i , sont les indices de commandabilité.
i
(iii) On calcule l'inverse −1 et on la met sous la forme :
1T
T i
−1 2
= , où : k est la ième ligne avec : k i = j , i = 1, ... , m.
T
i
T j=1
n
(iv) Avec les lignes Tk , on forme la matrice de passage T qui se présente comme suit :
i
T
k1
T
A
k1
T 1 −1
A
T = k1
T
km
T Am −1
k m
(v) La forme ( A , B , C ) est donnée par : A = T A T −1 , B = T B et C = CT −1 avec :
A11 A1m B1
A= et B=
A m1 A mm Bm
où, pour : i,j = 1, ... , m, les blocs des matrices A ii , de dimension (i x i), Aij , de dimension
Chapitre 2 -4- M. GASMI
Cours de systèmes multivariables
(i x j) et Bi , de dimension (i x m) , sont respectivement données par les formes :
0 1 0 0
0 0 0 0 0
1 0
Aii = 0 , Aij = et Bi =
0 0 0 0
0 0 1
x x x x x x 0 0 1 x x
La dernière ligne des matrices Bi débute par des zéros jusqu'à la colonne (i–1), ensuite, on
place 1 dans la ième colonne ; le reste des éléments sont quelconques. La matrice C n'a pas de
forme particulière.
Exemple : Soit un système, d'ordre 3 et ayant 2 entrées, décrit par les matrices A et B
suivantes :
1 2 3 1 0
A= 2 3 4 et B = 0 1
3 4 5 0 0
La matrice de commandabilité correspondante est donnée comme suit :
c = b1 b 2 | Ab1 Ab 2 | A 2b1 A 2b 2
1 0 1 2 14 20
= 0 1 2 3 20 29
0 0 3 4 26 38
On constate que les trois premières colonnes sont linéairement indépendantes ; on les arrange
1 1 0
donc comme suit pour obtenir la matrice suivante : = [b1 Ab1 b2] = 0 2 1
0 3 0
On voit bien que : 1 – 1 = 1 (l'exposant de A pour b1) 1 = 2
2 – 1 = 0 (l'exposant de A pour b2) 2 = 1
On calcule l'inverse de la matrice , on obtient :
1
1 0 − 3 T
1
−1 = 0 0 = T
1
3
2
T
0 1 − 2 3
3
1 2
D'un autre côté, on a : k1 = j = 1 = 2 et k 2 = j = 1 + 2 = 3 , ce qui donne :
j=1 j=1
Tk = T2 et Tk = 3T
1 2
Il vient la matrice de passage T telle que :
Chapitre 2 -5- M. GASMI
Cours de systèmes multivariables
1
0 0 23 4
T 3
− 1 −
2 3 3
4 5 −1
T = 2 A = 1
T
T = 2 0 1
3 3 3
3
T 0 0
0 1 − 2
3
Ce qui conduit à la forme canonique de commandabilité suivante :
0 1 0 0 0
B1
−1 A11 A12 80 26 10 4
A =T AT = = et B = T B = = 1 .
A 21 A 22 9 3 9 B2 3
8 1 0 1
0
3 3
Les éléments en gras peuvent constituer des balises ; elles sont connues à l'avance.
III.1.2. Forme canonique d'observabilité
De même, pour le système (II.1), on obtient la matrice d'observabilité suivante :
o = [CT ATCT ... A(n–1)TCT]
qui se présente comme suit :
(n −1)T T (n −1)T T
= c1T cT2 T T T
cl A c1
T T
A cl A c1
2T T 2T T
A cl A c1 A cl
CT ATCT A2TCT A(n–1)TCT
Algorithme à suivre :
(i) Inspecter les colonnes de la gauche vers la droite et tirer les n premiers vecteurs
linéairement indépendantes.
(ii) Arranger ceux-ci pour former la matrice suivante :
= c1T AT c1T A (1 −1)T c1T cT A T cT A ( 2 −1)T cT cT A (l −1)T cT
2 2 2 l l
Les coefficients i, ou encore max i , sont les indices d'observabilité.
i
(iii) On calcule l'inverse −1 et on la met sous la forme :
1T
T i
−1 2
= , où : k est la ième ligne avec : k i = j , i = 1, ... , l.
T
i
T j=1
n
(iv) Avec les lignes Tk , on forme la matrice de passage T qui se présente comme suit :
i
T = k1 A k1 A1 −1 k1 kl Al −1 kl
(v) La forme ( A , B , C ) est donnée par : A = T −1 A T , B = T −1 B et C = CT , avec :
A11 A1l
A= et C = C1 Cl
Al1 All
Chapitre 2 -6- M. GASMI
Cours de systèmes multivariables
où, pour : i,j = 1, ... , l, les blocs des matrices A ii , de dimension (i x i), Aij , de dimension
(i x j) et Ci , de dimension (l x i) , sont respectivement données par les formes :
0 0 0
0 0 0 x
1 0 0 x
x 0
Aii = 0 1 , Aij = et C =
i 1
0 x x
0 0 1 x
0 0 x
0 0 x
D'une façon similaire à la matrice Bi , la dernière colonne des matrices Ci débute par des
zéros jusqu'à la ligne (i–1), ensuite, on place 1 dans la ième ligne ; le reste des éléments sont
quelconques. La matrice B n'a pas de forme particulière.
Exemple : Soit un système, d'ordre 3 et ayant 2 sorties, décrit par les matrices A et C
suivantes :
1 2 0
0 1 0 c1
A = −3 −4 1 et C = =
0 0 1 c2
1 1 −2
La matrice d'observabilité est donnée par :
o = c1T cT2 | A T c1T A T cT2 | A 2T c1T A 2T cT2
0 0 −3 x x x
= 1 0 4 x x x
0 1 1 x x x
On forme la matrice de la façon suivante :
0 −3 0
= c1T A T c1T cT2 = 1 4 0
0 1 1
avec : 1 – 1 = 1 1 = 2 et 2 – 1 = 0 2 = 1
4
− 3 1 0 T
1
−1 1
= − 0 0 = T2
3
T
1 0 1 3
3
1
1
On a : k1 = j = 1 = 2 T
k1
= T
2 = − 0 0
j=1 3
2
1
k 2 = j = 1 + 2 = 3 T
k2
= 3T = 0 1
j=1 3
Chapitre 2 -7- M. GASMI
Cours de systèmes multivariables
1 1 1 2
− 3 − 3 3 − 3 − 3 1
Il vient : T = k 2
A k2 k3 = 0 1 0 T −1 = 0 1 0
1 1
0 − 1 0 1
3 3
Ce qui donne :
13 8
0 − 9 − 3
0 1 0
−1 A11 A12 10 T T
A=TAT = = 1 − 0 et C = CT = C1 C2 = 1
−
21
A A 22 3
0 1
2 5 3
0 −
9 3
De même, les éléments en gras peuvent constituer des balises ; elles sont connues à l'avance.
III.2. Cas de la matrice fonction de transfert
Pour une matrice fonction de transfert G(p), de dimension (l x m), on distingue deux formes
standards : le forme de Smith et la forme de Mc Millan.
Comme on a vu dans le chapitre précédent, G(p) peut être écrite sous la forme :
1
G(p) = N(p)
d(p)
avec :
– d(p) est le plus petit commun dénominateur de tous les éléments de G(p),
– N(p) est une matrice polynômiale (ses éléments sont des polynômes).
On note par fi(p), qui doit être monique, le plus grand facteur commun de tous les mineurs
d'ordre i de N(p). Par convention, on prendra : f0(p) = 1.
III.2.1. Forme de Smith
Selon les paramètres m et l, la forme de Smith est présentée comme suit :
– si : m > l, on a : S(p) = diag(i (p)) Ol , m−l
– si : m = l, on a : S(p) = diag(i (p))
diag( i (p))
– si : m < l, on a : S(p) =
O
l − m, m
f (p)
avec : i (p) = i
fi −1(p)
III.2.2. Forme de Mc Millan
La forme de Mc Millan est obtenue à partir de la matrice S(p) selon l'expression suivante :
1
M(p) = S(p)
d(p)
Chapitre 2 -8- M. GASMI
Cours de systèmes multivariables
Exploitation de la matrice M(p) : Après toutes les simplifications possibles, les pôles du
système sont tous les zéros des dénominateurs des éléments de M(p) tandis que les zéros sont
tous les zéros des numérateurs.
Exemple 1 : Soit à déterminer les pôles et les zéros de la matrice G(p) définie par :
1 2
p +1 p + 3 1 p + 3 2(p + 1)
G(p) = =
1 1 (p + 1)(p + 3) p + 3 p + 3
p +1 p +1
p + 3 2(p + 1)
On a : d(p) = (p+1) (p+3) et N(p) =
p + 3 p + 3
Ce qui donne : f0(p) = 1, f1(p) = 1 et f2(p) = |N(p)| = – (p + 3) (p – 1)
Comme les éléments f1(p) doivent être moniques, on prendra : f2(p) = (p + 3) (p – 1), ce qui
f (p) f (p)
conduit à : 1(p) = 1 = 1 et 2 (p) = 2 = (p + 3)(p − 1)
f0 (p) f1(p)
Ce qui donne, puisque m = l, la matrice de Smith sous la forme :
(p) 0 1 0
S(p) = 1 =
0 1(p) 0 (p + 3)(p − 1)
Elle conduit à la matrice de Mc Millan suivante :
1
0
1 1 0 (p + 3)(p + 1)
(p + 1)(p + 3) 0 (p + 3)(p − 1)
M(p) = =
(p − 1)
0
(p + 1)
Ce qui correspond à un seul zéro : (– 1) et trois pôles : (– 3) simple et (– 1) double.
Exemple 2 : Soit à déterminer les pôles et les zéros de la matrice G(p) définie par :
1 2
p +1 p + 3
p + 3 2(p + 1)
1 1 1 p + 3 p + 3
G(p) = =
p + 1 (p + 1)(p + 3)
p +1 p + 1 2(p + 3)
1 2
p + 3 p +1
p + 3 2(p + 1)
On a : d(p) = (p+1) (p+3) et N(p) = p + 3 p + 3
p + 1 2(p + 3)
Ce qui donne : f0(p) = 1, f1(p) = 1 et
p + 3 2(p + 1)
f21(p) = |N(p)|21 = = (p + 3) (p – 1) (monique)
p+3 p+3
p + 3 2(p + 1)
f22(p) = |N(p)|22 = = (p + 2) (monique)
p + 1 2(p + 3)
Chapitre 2 -9- M. GASMI
Cours de systèmes multivariables
On voit qu'il n'est pas nécessaire de calculer le troisième mineur puisque, pour les deux
premiers, ils n'ont pas de facteur commun f2(p) = 1.
1
(p + 1)(p + 3) 0
1 0
1
Ce qui conduit à : S(p) = 0 1 M(p) = 0
(p + 1)(p + 3)
0 0
0 0
Donc on n'a pas de zéro et on a : (– 1) et (– 3) des pôles doubles.
Exemple 3 : Même question que celle de l'exemple 2 mais pour une matrice G(p) définie par :
1 1 1
p +3 p +3 p+3
G(p) =
p + 2 p + 2 2(p + 2)
p +1 p + 3 p + 1
1 p +1 p +1 p +1
= (p + 2)(p + 3) (p + 1)(p + 2) 2(p + 2)(p + 3
(p + 1)(p + 3)
p +1 p +1 p +1
On a : d(p) = (p+1) (p+3) et N(p) =
(p + 2)(p + 3) (p + 1)(p + 2) 2(p + 2)(p + 3
Ce qui donne : f0(p) = 1, f1(p) = 1 et
p +1 p +1
f21(p) = |N(p)|21 = = (p + 1)(p + 2) (monique)
(p + 2)(p + 3) (p + 1)(p + 2)
p +1 p +1
f22(p) = |N(p)|22 = = (p + 1)(p + 2)(p + 3) (monique)
(p + 2)(p + 3) 2(p + 2)(p + 3)
p +1 p +1
f23(p) = |N(p)|23 = = (p + 1)(p + 2)(p + 5) (monique)
(p + 1)(p + 2) 2(p + 2)(p + 3)
Ce qui donne : f2(p) = (p + 1)(p + 2)
1
0 0
1 0 0 (p + 1)(p + 3)
Il vient : S(p) = M(p) = (p + 2)
0 (p + 1)(p + 2) 0 0
0
(p + 3)
Donc on a (–2) comme zéro et trois pôles : (– 1) simple et (– 3) double.
Chapitre 2 -10- M. GASMI
Vous aimerez peut-être aussi
- Chapitre 3Document6 pagesChapitre 3kawtherPas encore d'évaluation
- TP Multivariable: Etude D'un Réservoir D'eau: Master: Contrôle, Informatique Industrielle, Signaux Et SystèmesDocument7 pagesTP Multivariable: Etude D'un Réservoir D'eau: Master: Contrôle, Informatique Industrielle, Signaux Et SystèmesSafaePas encore d'évaluation
- TDasservissementDocument10 pagesTDasservissementSIDATIPas encore d'évaluation
- 2-Série TD EE PDFDocument2 pages2-Série TD EE PDFHfgjjPas encore d'évaluation
- Mai 2015Document6 pagesMai 2015Ali brahim MahamatPas encore d'évaluation
- Stabilite Des Systemes Lineaires 2Document12 pagesStabilite Des Systemes Lineaires 2Moubarak Abdoulnassour100% (1)
- TP AutomatiqueDocument24 pagesTP AutomatiqueHoussam Haddani100% (1)
- Asservissement Cour 2Document5 pagesAsservissement Cour 2drizihamzaPas encore d'évaluation
- td2 - Représentation D'étatDocument3 pagestd2 - Représentation D'étatCode CodeurPas encore d'évaluation
- Systèmes Du Second Ordre PDFDocument6 pagesSystèmes Du Second Ordre PDFTony TonyPas encore d'évaluation
- Systèmes Du Second OrdreDocument6 pagesSystèmes Du Second Ordretrawri007Pas encore d'évaluation
- TP1 Asservissement ING1 ISIMMDocument8 pagesTP1 Asservissement ING1 ISIMMlahmar RayenPas encore d'évaluation
- Chapitre 3 - SLMDocument4 pagesChapitre 3 - SLMmohamed kolliPas encore d'évaluation
- TD PDFDocument20 pagesTD PDFabidinePas encore d'évaluation
- Auto CttransfertDocument15 pagesAuto CttransfertMaher Chi ChibaniPas encore d'évaluation
- TD Atomatique Avancee 2021Document20 pagesTD Atomatique Avancee 2021souhil berrahalPas encore d'évaluation
- Auto1 Exercices2Document2 pagesAuto1 Exercices2Julien FernandezPas encore d'évaluation
- TP 2 CommandeDocument14 pagesTP 2 CommandeDilekh AnisPas encore d'évaluation
- Chapitre 1 Avec Exemples D'applicationsDocument10 pagesChapitre 1 Avec Exemples D'applicationsMohammed ALMUSHIAAPas encore d'évaluation
- 5385 B 108129 DDDocument5 pages5385 B 108129 DDImmamHadramy100% (1)
- TPs Automatique 1Document6 pagesTPs Automatique 1HolaPas encore d'évaluation
- TP2 Auto WissalDocument10 pagesTP2 Auto WissalWissal MNARIPas encore d'évaluation
- TD 01 GPCDocument2 pagesTD 01 GPCkhaledteslaPas encore d'évaluation
- Cours MAP434: Contrôle de Modèles Dynamiques Séance 1, 06 Mars 2019 Contrôlabilité Des Systèmes LinéairesDocument6 pagesCours MAP434: Contrôle de Modèles Dynamiques Séance 1, 06 Mars 2019 Contrôlabilité Des Systèmes LinéairesAurelien YeremouPas encore d'évaluation
- TP1 MatlabDocument5 pagesTP1 MatlabwalidPas encore d'évaluation
- Chapitre 1 ASC 22Document35 pagesChapitre 1 ASC 22Aymen BhdPas encore d'évaluation
- 2021 2022 TD Commande Optimale LQRDocument1 page2021 2022 TD Commande Optimale LQRmarwane kamili100% (1)
- TD Automatique 1A JMD 2011Document20 pagesTD Automatique 1A JMD 2011Hajri MohamedPas encore d'évaluation
- ExercicesDocument7 pagesExercicesTasnim amdouniPas encore d'évaluation
- Projet 1100Document13 pagesProjet 1100Sofiane BenbraikPas encore d'évaluation
- Chapitre 4 Transformee en ZDocument7 pagesChapitre 4 Transformee en ZGray AbPas encore d'évaluation
- Auro1a2 TPDocument3 pagesAuro1a2 TPAzou Azzeddine AzzeddinePas encore d'évaluation
- 2020-TP5Document4 pages2020-TP5nevilleilunga5Pas encore d'évaluation
- Devoir Auto2 19-20Document5 pagesDevoir Auto2 19-20Houda BourimechPas encore d'évaluation
- Chapitre 4 Fonction de Transfert Et Schemas Blocs Et DiagrammesDocument7 pagesChapitre 4 Fonction de Transfert Et Schemas Blocs Et DiagrammesxBlack-Gamer3 JalilPas encore d'évaluation
- Chapitre 5 Fonction Transfert Schemas Blocs DiagrammesDocument7 pagesChapitre 5 Fonction Transfert Schemas Blocs DiagrammesWardat Eljanoud SouklahadPas encore d'évaluation
- TP 3 ModDocument7 pagesTP 3 ModabdousewagerPas encore d'évaluation
- Chapitre 3Document11 pagesChapitre 3fihakhir aminePas encore d'évaluation
- Compte Rendu D'automatiqueDocument12 pagesCompte Rendu D'automatiqueMOHAMED TAMZAITIPas encore d'évaluation
- TPIdentification ET Régulation (ZENDAOUI Elmehdi Gecsi-2)Document10 pagesTPIdentification ET Régulation (ZENDAOUI Elmehdi Gecsi-2)Mehdi ZendaouiPas encore d'évaluation
- Chapitre 3 - SLMDocument5 pagesChapitre 3 - SLMMuhammad BneijaraPas encore d'évaluation
- BTS GR - A Mai 2013Document7 pagesBTS GR - A Mai 2013Adoudi DoudiPas encore d'évaluation
- tp3 CommandeDocument6 pagestp3 CommandeabdousewagerPas encore d'évaluation
- TDN 3Document3 pagesTDN 3Mazen TouaitiPas encore d'évaluation
- 2020 2021 Représentation D'état Chapitre 3Document25 pages2020 2021 Représentation D'état Chapitre 3Mounaim MatiniPas encore d'évaluation
- Correction td3Document5 pagesCorrection td3GxfhjjPas encore d'évaluation
- Soit Un Système de Second Ordre Défini Par La Fonction de Transfert en Boucle OuverteDocument3 pagesSoit Un Système de Second Ordre Défini Par La Fonction de Transfert en Boucle OuverteamalPas encore d'évaluation
- Cours Auto Chapitre 1Document4 pagesCours Auto Chapitre 1Nabil TAALLAHPas encore d'évaluation
- Corrigé D'examen - Systèmes Multivariables 2016 - 2017Document4 pagesCorrigé D'examen - Systèmes Multivariables 2016 - 2017Nadir BouhaddaPas encore d'évaluation
- TP N°3Document7 pagesTP N°3ddPas encore d'évaluation
- Exercices d'intégrales de lignes, de surfaces et de volumesD'EverandExercices d'intégrales de lignes, de surfaces et de volumesPas encore d'évaluation
- Exercices d'intégrales et d'équations intégro-différentiellesD'EverandExercices d'intégrales et d'équations intégro-différentiellesPas encore d'évaluation
- Série Champ Magnétique Web PDFDocument3 pagesSérie Champ Magnétique Web PDFNassim Chraiti100% (1)
- Chaos en Mecanique QuantiqueDocument160 pagesChaos en Mecanique QuantiqueJean philippe PayetPas encore d'évaluation
- 1 - TD13 Cinématique Schémas CinématiquesDocument6 pages1 - TD13 Cinématique Schémas CinématiquesCorentin ProdPas encore d'évaluation
- Elfi Dic2 2019Document211 pagesElfi Dic2 2019IbrahimPas encore d'évaluation
- Série 1 Electricité1 PDFDocument2 pagesSérie 1 Electricité1 PDFOtman RamliPas encore d'évaluation
- Nouveau Programme 1èreDocument16 pagesNouveau Programme 1èreAntoine GressetPas encore d'évaluation
- Alge Bre 8-2 2023-2024Document6 pagesAlge Bre 8-2 2023-2024Jacques GerardinPas encore d'évaluation
- Intégrale de Surface - WikipédiaDocument6 pagesIntégrale de Surface - Wikipédiagloiredinho242Pas encore d'évaluation
- TD Espaces Vectoriels Et Applications Linéaires PDFDocument7 pagesTD Espaces Vectoriels Et Applications Linéaires PDFFogang Zacharie TenePas encore d'évaluation
- Espace Vectoriel Euclidien Produit Scala PDFDocument15 pagesEspace Vectoriel Euclidien Produit Scala PDFRAKOTOMALALAPas encore d'évaluation
- Arnold - Trivium Mathematique (Exos Math)Document14 pagesArnold - Trivium Mathematique (Exos Math)paulb75Pas encore d'évaluation
- BenkiniouarDocument8 pagesBenkiniouarFahem OuazenePas encore d'évaluation
- Geometrie Dans L Espace Resume de Cours 2Document2 pagesGeometrie Dans L Espace Resume de Cours 2mohmedPas encore d'évaluation
- Chapitre 1 TensorielDocument16 pagesChapitre 1 TensorielPape Moussa DiopPas encore d'évaluation
- TenseurDocument59 pagesTenseurAnas Kerty100% (1)
- Mode GlissantDocument6 pagesMode GlissantDîɖEn ElkêBîrPas encore d'évaluation
- Mécanique Des SolidesDocument78 pagesMécanique Des Solidesslimi83% (6)
- Algèbre 3Document291 pagesAlgèbre 3Kodjo Gabin DEGUENON100% (1)
- Chapitre 04Document47 pagesChapitre 04Mariona AutranPas encore d'évaluation
- Maths Centrale PSI 2002 M2 (Enoncé)Document6 pagesMaths Centrale PSI 2002 M2 (Enoncé)LM --Pas encore d'évaluation
- TP Sur Les Lois de NewtonDocument5 pagesTP Sur Les Lois de NewtonmedinaPas encore d'évaluation
- Problèmes de Lieux Géométriques 37: Définition D'introductionDocument18 pagesProblèmes de Lieux Géométriques 37: Définition D'introductionIgnace BagrePas encore d'évaluation
- Agrégation Algèbre Et Géométrie Euclidienne Et Hermitienne - Frédéric PaulinDocument149 pagesAgrégation Algèbre Et Géométrie Euclidienne Et Hermitienne - Frédéric PaulinmohamedefarouePas encore d'évaluation
- Resume Du Cours Electrocinetique 2020 (1) : June 2020Document15 pagesResume Du Cours Electrocinetique 2020 (1) : June 2020adadadPas encore d'évaluation
- Cours Calcul VectorielDocument15 pagesCours Calcul VectorielBrahim MouhcinePas encore d'évaluation
- Chapitre 2. Systèmes de Forces THDocument25 pagesChapitre 2. Systèmes de Forces THsinaly coumarePas encore d'évaluation
- Support Cours MecaAppli 2022 2023 GMDocument170 pagesSupport Cours MecaAppli 2022 2023 GMnouhaila RahmouniPas encore d'évaluation
- Psi MathsDocument26 pagesPsi MathsMoustakimPas encore d'évaluation
- Matrice Sous MatlabDocument71 pagesMatrice Sous Matlabhitmann47Pas encore d'évaluation