NOUVELLE FORMULATION DE L’ÉTUDE DE LA

FLEXION TRANSVERSALE SUIVANT LA MÉTHODE

DE MM. GUYON ET MASSONNET

La méthode de calcul des effets de la flexion transversale dans les tabliers de ponts dalles ou de ponts à pou-
tres multiples par la méthode dite de « Guyon – Massonnet », basée sur la théorie des dalles orthotropes, est
encore très utilisée par les bureaux d’études.
Malgré les perfectionnements successifs qui lui ont été apportés, elle souffre de certains inconvénients gê-
nants :
− Les résultats pratiques sont présentés à la fois sous forme de tables, incompatibles avec les moyens de
calcul actuels, et sous une forme analytique compliquée, se prêtant mal à la programmation, et encore
moins à des opérations très utiles en pratique, telles que la dérivation ou l’intégration.
− Il n’est pas possible de prendre en compte un coefficient de Poisson ν non nul lorsque la dalle n’est pas
isotrope, ce qui introduit une discontinuité dans la méthode, qui ne donne le choix qu’entre les formules
relatives aux dalles isotropes, avec ν quelconque, et celles relatives aux dalles orthotropes, avec ν = 0 .
− Dans la pratique, on rencontre souvent des coefficients de torsion α supérieurs à 1, pour lesquels la mé-
thode n’a pas été développée.
La présente étude tente de pallier ces inconvénients, en suivant la même démarche que celle de MM. Guyon
et Massonnet, mais en résolvant l’équation qui en résulte de manière un peu différente, aboutissant à des
calculs simples, faciles à programmer, et très généraux.
En outre, la méthode initiale n’a été développée que pour des dalles à bords libres. La présente approche
autorise d’imposer très simplement des conditions aux limites quelconques sur les deux bords latéraux de la
dalle, ce qui permet d’une part l’étude de la flexion locale des hourdis et d’autre part l’assemblage des matri-
ces de rigidité de plusieurs dalles contiguës. Cette dernière possibilité est notamment utile pour l’étude des
ponts à nervures ou des ponts comportant des poutres différentes, à la fois sous l’aspect de la flexion locale
et de la flexion générale et constitue ainsi une généralisation de la méthode de dite de « Cart – Fauchart ».
Cet article comporte deux parties :
− Formulation générale et étude des cas de base, qui développe l’analyse du problème et donne ses solu-
tions analytiques. Elle s’achève par une comparaison avec les résultats donnés par un programme à bar-
res, qui met en évidence une excellence concordance entre les deux méthodes.
− Étude d’un ensemble de dalles contiguës, appuyées ou non sur des poutres, qui constitue la généralisation
de la méthode pour l’étude des ponts à poutres ou à nervures. Cette partie s’achève par une comparaison
avec une étude aux éléments finis.
Signalons que la méthode d’origine a donné lieu à de très nombreuses publications et développements par
différents auteurs ; la bibliographie placée en fin d’article est de ce fait volontairement très succincte. En
pratique, nous nous sommes essentiellement appuyés sur le livre très complet de MM. Barès et Massonnet
« Le calcul des grillages de poutres et dalles orthotropes », cité en référence [1] de la bibliographie (cet ou-
vrage comporte lui-même 159 références bibliographiques !).
Signalons enfin que tous les calculs formels ont été vérifiés à l’aide du logiciel Maple 7.

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 1

 PREMIÈRE PARTIE : FORMULATION GÉNÉRALE

1) Théorie de la plaque orthotrope symétrique

Les hypothèses de base exposées en [1] concernant les plaques orthotropes aboutissent à des relations de la
forme :
⎡ Ex
⎡ Ex ε x = σ x − ν x σ y ⎡σ x = Ex ε x + ν x E y ε y ⎢ Ex = 1 − ν ν
⎢ ⎢ ⎢ x y
⎢ Eyε y = σ y − ν yσx soit: ⎢σ y = E y ε y + ν y Ex ε x avec: (1.1)
⎢ Ey
⎢ 2Gε xy = τ xy ⎢ τ xy = 2Gε xy ⎢ Ey =
⎣ ⎣ 1 − νxν y
⎢⎣

sachant que le théorème de Maxwell et Betti impose E y ν x = Ex ν y .

Suivant les hypothèses des plaques, on peut écrire :

∂u ∂2 w ∂v ∂2 w 1 ⎛ ∂u ∂v ⎞ ∂2w
εx = = −z 2 εy = = −z 2 ε xy = ⎜ + ⎟ = − z (1.2)
∂x ∂x ∂y ∂y 2 ⎝ ∂y ∂x ⎠ ∂x ⋅ ∂y

Les conventions de signe utilisées sont celles de la mécanique, à savoir σ > 0 pour les tractions. Les mo-
r
ments fléchissants et les efforts tranchants sont quant à eux définis de telle sorte que, si n désigne la normale
r r
à une facette portée par le plan XOY, les composantes du moment m et de l’effort tranchant q par unité de
longueur exercé par l’extérieur de la facette sur l’intérieur soient :

Qx Qy

d y ⎛ mx ⎞ ⎛ M xy −M y ⎞
⎜ ⎟ ⎜ ⎟ ⎛ nx ⎞
⎜ my ⎟ = ⎜ M x M yx ⎟ ⋅ ⎜ ⎟ (1.3)
ny
Mxy
⎜q ⎟ ⎜ Q
⎝ z⎠ ⎝ x Qy ⎟⎠ ⎝ ⎠
x -My
Mxy Mx

Ces conventions, peu habituelles, sont choisies pour préserver la cohérence avec les ouvrages [1] et [2] ( M x
porté par OY, M y porté par OX). En reportant les expressions (1.2) dans (1.1) et en intégrant, il vient :

⎡ d/ 2
∂2w ∂2w ⎡ d3 ( EI ) x
⎢ M x = ∫ σ x z ⋅ dz = −ρ x 2 − ρ xy 2 ⎢ρ x = E x =
⎢ − d/ 2
∂x ∂y ⎢ 12 1 − ν x ν y
⎢ d/ 2
∂ w
2
∂2w ⎢ d3 ( EI ) y d3
⎢ M y = ∫ σ y z ⋅ dz = −ρ y 2 − ρ xy 2 avec : ⎢ρ y = E y = γ=G
⎢ − d/ 2
∂y ∂x ⎢ 12 1 − ν x ν y 12
⎢ ⎢
⎢ρ xy = ν x ρ y = ν y ρ x
d/ 2
⎢ M = − τ z ⋅ dz = − M = 2γ ∂ w
2

⎢ xy
⎣
∫ xy
− d/ 2
yx
∂x ⋅ ∂y ⎢⎣

La suite des calculs est développée dans tous les ouvrages traitant de la théorie des plaques (cf. [1], [2], [3]).
Notamment, l’équilibre des moments permet d’exprimer les efforts tranchants par :
⎡ ∂M x ∂M yx ∂3w ∂3 w
⎢ xQ =
∂x
+
∂y
= −ρ x
∂x 3
− ( 2 γ + ρ xy )
∂x ⋅ ∂y 2
⎢ (1.4)
⎢ ∂M y ∂M xy ∂3 w ∂3w
⎢Q y = − = −ρ y 3 − ( 2γ + ρ xy )
⎢⎣ ∂y ∂x ∂y ∂y ⋅ ∂x 2

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 2

L’équilibre des forces verticales impose quant à lui :
∂Qx ∂Qy ∂4w ∂4 w ∂4w
+ = − p ( x, y ) ⇒ ρx + 2(2 γ + ρ xy ) + ρ y = p ( x, y ) (1.5)
∂x ∂y ∂x 4 ∂x 2 ⋅ ∂y 2 ∂y 4

Cette dernière relation, variante de l’équation de Lagrange, constitue l’équation fondamentale de la plaque.
Comme il est également exposé dans [1], [2] et [3], cette équation ne possède pas suffisamment de degrés de
liberté pour pouvoir exprimer toutes les conditions aux limites et, en particulier, que les moments de torsion
sont nuls sur les bords de la plaque. Ce problème, traité par Kirchhoff, peut être « contourné » en considérant
que les efforts tranchants doivent être remplacés sur les bords de la plaque par des efforts « corrigés », valant
respectivement suivant les bords parallèles à y et à x :
⎡ ∂M xy ∂3 w ∂3w
⎢Qx = Qx − = −ρ x 3 − (4γ + ρ xy )
⎢ ∂y ∂x ∂x ⋅ ∂y 2
(1.6)
⎢ ∂M yx ∂3 w ∂3w
⎢Q y = Q y + = −ρ y 3 − (4γ + ρ xy )
⎢⎣ ∂x ∂y ∂y ⋅ ∂x 2

2) Étude d’un grillage de poutres de même hauteur

Le présent paragraphe a pour seul objet d’étendre la théorie d’origine par l’introduction de la notion de
« coefficient de Poisson équivalent », ν , qui permet de prendre en compte l’influence de ν pour une dalle
orthotrope quelconque. On se borne à étudier un grillage de poutres rectangulaires composées du même ma-
tériau et de même hauteur, suivant le schéma ci-après :
y L
On pose : k x =
∑b i
ky =
∑a i

2B L

b a Par analogie avec l’étude du paragraphe (1), on cher-

che une relation de la forme :
2B x ⎡ ∂2w ∂2 w
M
⎢ x = a x + bx
⎢ ∂x 2 ∂y 2
(2.1)
B0 L0 ⎢ ∂2 w ∂2w
⎢ M y = a y 2 + by 2
⎢⎣ ∂y ∂x

Introduisons une courbure constante ( ∂ 2 w / ∂x 2 ) et admettons que σ y = 0 sur les poutres, (1.1) et (1.2)
permettent d’écrire :
1 ∂2w ν ∂2 w
εx = σx = − z 2 εy = − σx = −z 2
E ∂x E ∂y

Faisons l’hypothèse un peu « brutale » mais exacte aux deux limites( k x = 0 , k x = 1 ) que les entretoises se
déforment sous l’effet du coefficient de Poisson dans leurs parties communes avec les poutres. Dans ces
conditions, l’allongement global d’une entretoise à la cote z vaut :
ν (1+εyp) bi
δ = ε yp ∑ bi = − σ x ∑ bi = −ν ⋅ ε x ∑ bi
E
soit une déformation moyenne :
y
δ ∂2w ∂2 w
εy = = −ν ⋅ ε x k x = ν ⋅ k x z 2 = − z 2 entretoise
2b ∂x ∂y
poutre

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 3

La courbure ( ∂ 2 w / ∂x 2 ) des poutres entraîne donc une courbure moyenne des entretoises :

∂2w ∂2 w
= −ν ⋅ k x avec : M y = 0
∂y 2 ∂x 2

En remplaçant dans (2.1) puis par symétrie, on trouve : by = ν ⋅ a y k x bx = ν ⋅ ax k y .

EI x EI y
ainsi que : ax = − ay = −
1 − ν2kx k y 1 − ν2kx k y

Soit, finalement :
⎡ ⎛ ∂2w ∂2w ⎞ ⎡ EI x d3
M
⎢ x = −ρ P⎜ + ν ⎟ ⎢ρ P = ν x = ν ⋅ kx I x = kx
⎢ ⎝ ∂x
2 y
∂y 2 ⎠ ⎢ 1 − ν xν y 12
⎢ avec : (2.2)
⎛ 2 ∂2w ⎞ ⎢ EI y d3
⎢ M y = −ρ E ⎜ ∂ w + ν ⎟ ⎢ρ E = ν y = ν ⋅ ky I y = ky
⎢⎣ ⎝ ∂y
2 x
∂x 2 ⎠ ⎣⎢ 1 − ν xν y 12

qui vérifie bien ρ P ⋅ ν y = ρ E ⋅ ν x .

On trouve donc des relations analogues à celles de la plaque orthotrope avec des coefficients de Poisson :
ν x = ν ⋅ kx ν y = ν ⋅ ky

Comme, dans les cas courants, k x << 1 , k y << 1 , et ν ≤ 0,5 , on conçoit que l’influence du coefficient de
Poisson soit minime dans le cas d’un grillage de poutres. En poursuivant le raisonnement de [1], mais sans
négliger le coefficient de Poisson, on arrive à l’équation :
∂4 w ⎛ γP + γE ⎞ ∂ w ∂4 w
4
ρP + 2 ⎜ + ν ⋅ ρ ρ
P E ⎟ + ρ E = p ( x, y ) (2.3)
∂x 4 ⎝ 2 ⎠ ∂x ⋅ ∂y
2 2
∂y 4

où l’on a posé :
ν = ν xν y = ν kx k y ⇒ ρ P ⋅ ν y = ρ E ⋅ ν x = ν ⋅ ρ Pρ E

et où γ P et γ E représentent les rigidités de torsion des poutres et des entretoises par unité de longueur :
Cp CE EK i
γP = γE = Ci = GK i =
B0 L0 2(1 + ν )

L’équation (2.3) est donc formellement identique à l’équation (1.5) avec :

ρP = ρx ρE = ρ y γ P + γ E = 4γ (2.4)

Par commodité pour la suite, on écrira l’équation (2.3) sous la forme :

ρP ∂ 4 w ρP ∂ 4 w ∂ 4 w p ( x, y )
+ 2 α + =
ρ E ∂x 4 ρ E ∂x 2 ⋅ ∂y 2 ∂y 4 ρE
(2.5)
γP + γE
α= +ν paramètre de torsion
2 ρPρE

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 4

Par ailleurs, on tire de (1.4), (1.6), (2.2), des équivalences (2.4) et de la définition de α :
⎡ ⎛ ∂2w ρE ∂ 2 w ⎞ ⎛ ∂2 w ρ ∂2w ⎞
⎢ M x = −ρ P ⎜⎜ 2 + ν ⎟ M y = −ρ E ⎜⎜ 2 + ν P ⎟
⎢ ⎝ ∂x ρ P ∂y 2 ⎟⎠ ⎝ ∂y ρ E ∂x 2 ⎟⎠
⎢ (2.6)
⎢Q = −ρ ⎛ ∂ w + α ρP ∂ w ⎞ ⎛ ∂3 w ρ ∂3w ⎞
3 3

⎜
⎜ ∂y 3 ⎟ Qy = −ρ E ⎜⎜ 3 + (2α − ν ) P ⎟
⎢ ρ E ∂y ⋅ ∂x 2 ⎟⎠ ρ E ∂y ⋅ ∂x 2 ⎟⎠
y E
⎣ ⎝ ⎝ ∂y

3) Résolution de l’équation de Lagrange

3.1) Généralités

z y L Considérons un grillage de poutres vérifiant les

hypothèses du paragraphe (2), chargé en y = 0 par
une charge de type « couteau », développée en
série de Fourier sous la forme :
x ∞
mπx
2b P ( x) = ∑ Pm ⋅ sin
m =1 L (3.1)

Suivant la méthode de Guyon et Massonnet, on cherche les solutions sous la forme d’une série de Lévy :
∞ ∞
mπx
w ( x, y ) = ∑ wm ( x, y ) = ∑ Wm ( y ) ⋅ sin (3.2)
m =1 m =1 L

Notons que cette forme implique w = 0 et ∂ 2 w / ∂x 2 = 0 pour x = 0 et x = L et n’est donc compatible

qu’avec une dalle sur appuis simples. Posons :
b ρP
θ= 4 paramètre d'entretoisement
L ρE
(3.3)
σ y L mπx x
σ m = mπθ βm = m Ym = σ m = βm y λm = Xm = =
b b mπ L λm

Avec ces notations, on obtient, pour le rang m :

ρP ∂2 1 ∂ ∂
= βm2 λ m2 =− 2 = βm
ρE ∂x 2
λm ∂y ∂Ym

L’équation (2.5) devient, en désignant par Wm( n ) (Ym ) la dérivée d’ordre n de Wm par rapport à Ym :
∞ p ( x, y )
∑β
m =1
4
m ⋅ ⎡⎣Wm(4) (Ym ) − 2α ⋅ Wm(2) (Ym ) + Wm (Ym ) ⎤⎦ ⋅ sin X m =
ρE
(3.4)

Dans la suite de ce paragraphe, nous nous intéresserons à la résolution de l’équation pour un harmonique m
donné, de ce fait, pour alléger les notations, l’indice m sera systématiquement omis.

3.2) Solution homogène

D’après (3.4), l’équation homogène pour chaque harmonique s’écrit :

WH( 4 ) (Y ) − 2α ⋅ WH( 2 ) (Y ) + WH (Y ) = 0 (3.5)

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 5

Posons :
⎡ 1+ α 1− α
⎢si α ≤ 1 r = cos µ = s = sin µ = ⇒ α = cos ( 2µ )
⎢ 2 2
⎢ 1+ α α −1
⎢si α ≥ 1 r = cosh µ = s = sinh µ = ⇒ α = cosh ( 2µ )
⎣ 2 2

Avec ces notations, les solutions de l’équation caractéristique sont :

⎡ r1234 = ± ( cos µ ± i ⋅ sin µ ) = ± ( r ± i ⋅ s ) si α ≤ 1
⎢
⎢⎣ r1234 = ± ( cosh µ ± sinh µ ) = ± ( r ± s ) si α ≥ 1

En pratique, pour des raisons de stabilité numérique et de symétrie, on choisit la famille de fonctions sui-
vante, qui prend des valeurs simples sur les bords de la dalle :
⎡ F0 (Y ) = cosch ⎡⎣ s ( σ − Y ) ⎤⎦ ⋅ e − r ( σ−Y )
⎢ ⎡ sin u
⎢ F1 (Y ) = −sinsh ⎡ s ( σ − Y ) ⎤ ⋅ e − r ( σ−Y )
⎣ ⎦ ⎢cosch u = cos u sinsh u =
s
si α ≤ 1
⎢ avec : ⎢
⎢ F2 (Y ) = cosch ⎡ s ( σ + Y ) ⎤ ⋅ e − r ( σ+Y ) ⎢cosch u = cosh u sinh u
⎢ ⎣ ⎦ sinsh u = si α ≥ 1
⎢⎣ s
⎢ F3 (Y ) = −sinsh ⎡ s ( σ + Y ) ⎤ ⋅ e − r ( σ+Y )
⎣ ⎣ ⎦

sinsh ( sY )
La fonction sinsh est introduite afin que ait pour limite Y lorsque µ → 0 (α → 1) .
s

En notant, comme pour W, F ( n ) la dérivée d’ordre n par rapport à Y des fonctions F et en étendant la nota-
tion à n < 0 pour des primitives particulières, on montre par récurrence que :
⎡ F0( n ) (Y ) = + cosch ⎡⎣ s ( σ − Y ) − nµ⎤⎦ ⋅ e ( )
− r σ−Y
= (−1) n F2( n ) ( −Y )
⎢
⎢ F1( n ) (Y ) = −sinsh ⎡⎣ s ( σ − Y ) − nµ⎤⎦ ⋅ e ( )
− r σ−Y
= (−1) n F3( n ) ( −Y )
⎢ (3.6)
⎢ F2( n ) (Y ) = (−1) n cosch ⎡ s ( σ + Y ) − nµ⎤ ⋅ e − r ( σ+Y ) = (−1) n F0( n ) ( −Y )
⎢ ⎣ ⎦
⎣ F3 (Y ) = −(−1) sinsh ⎡⎣ s ( σ + Y ) − nµ⎤⎦ ⋅ e = (−1) n F1( n ) ( −Y )
− r ( σ+Y )
⎢ ( n ) n

Par ailleurs, on montre facilement que ces fonctions sont également solutions de (3.5) pour tout n. Finale-
ment, la solution homogène peut être exprimée sous la forme :
3
WH (Y ) = ∑ Ai ⋅ Fi (Y ) WH (Y ) = [ F (Y ) ] ⋅[ A]
T
ou : (3.7)
i =0

3.3) Solution particulière

La dalle est supposée infiniment large et chargée par la charge de type « couteau » définie par (3.1). Par sy-
métrie, on peut se limiter à l’étude de y ≥ 0 . En dehors de l’axe y = 0 , qui constitue une singularité, la solu-
tion est une solution de type homogène, vue au paragraphe (3.2), avec la restriction que si l’on considère
y → ∞ , il ne doit pas rester d’exponentielle à coefficient positif. Par ailleurs, la dérivée doit être nulle en 0
par symétrie.
On montre finalement que W est de la forme :
WP (Y ) = W0 ⋅ sinsh ( sY + µ ) ⋅ e − rY

Ce qui amène à introduire la fonction représentative de la solution particulière, au facteur W0 près :

ϕ (Y ) = sinsh ( s Y + µ ) ⋅ e
−r Y

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 6

Cette fonction est formellement identique à F3( −1) ( Y ) , avec σ = 0 . On en déduit que les dérivées et des pri-
mitives particulières sont données par :

ϕ( n ) (Y ) = ( −sgn (Y ) ) ⋅ sinsh ( s Y − (n − 1)µ ) ⋅ e

n −r Y (3.8)

Avec sgn (Y ) = −1 pour Y < 0 et sgn (Y ) = +1 pour Y ≥ 0 , la dérivée donnée par cette expression en Y = 0
sera la dérivée à droite.

Il découle de même de cette similitude que les fonctions ϕ( n ) sont solutions de (3.5) pour tout n, en dehors de
Y = 0 . Pour trouver W0, exprimons l’effort tranchant d’après (2.6) en Y = 0 :
1 P
Qy = −W0 ⋅ ρ E ⋅β3 ⋅ ( ϕ(3) ( 0 ) − α ⋅ ϕ(1) ( 0 ) ) ⋅ sin X = − P ⋅ sin X ⇒ W0 =
2 4ρ E β3 r

D’où découle l’expression finale de la solution particulière :

P
⋅ sinsh ( s Y + µ ) ⋅ e
−r Y
WP (Y ) = = W0 ⋅ ϕ(Y )
4ρ E β r
3

Si l’on considère maintenant que l’on place la charge en y = e au lieu de 0, la solution devient :
P e
WP (Y ) = W0 ⋅ ϕ (Y − E ) W0 = avec : E = σ (3.9)
4ρ E β3 r b

Malgré les apparences, on vérifie bien par (3.3) que cette solution ne dépend pas de b.

3.4) Note sur l’intégration de la fonction φ

Comme il a été dit, l’expression (3.8) donne des primitives particulières de φ pour n < 0, qui ne permettent
pas dans le cas général de calculer des intégrales définies du type :
Y2

∫ ϕ (Y ) ⋅ dY = Φ (Y ) − Φ (Y )
Y1
2 1

qui nécessite que la fonction Φ soit continue, ce qui n’est pas le cas de ϕ( −1) .

De façon générale, les fonctions ϕ( n ) (Y ) sont continues en Y = 0 pour n pair et pour n impair, on a :

lim− ( ϕ (Y ) ) = +sinsh ( (1− n) µ) lim+ ( ϕ (Y ) ) = −sinsh ( (1− n) µ)

( n) ( n)

Y →0 Y →0

Pour n = –1, les limites à gauche et à droite sont donc respectivement 2r et –2r. Pour rendre la fonction
continue, il suffit donc de retrancher 2r pour Y < 0 et d’ajouter 2r pour Y ≥ 0 . On introduira donc les fonc-
tions continues :
ϕ(I −1) (Y ) = ϕ( −1) (Y ) + 2r ⋅ sgn (Y ) ϕ(I −2) (Y ) = ϕ( −2) (Y ) + 2r ⋅ Y (3.10)

Telles que :
Y Y

∫ ϕ ( α ) ⋅ d α = ϕI ( Y ) ∫ ϕ ( α ) ⋅ d α = ϕ (Y )
( −1) ( −1) ( −2)
I I
0 0

On notera que les fonctions ϕ(I −1) (Y ) et ϕ(I −2) (Y ) ne sont pas solutions de (3.5).

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 7

3.5) Conditions aux limites

La solution générale s’exprime en sommant (3.7) et (3.9) :

W (Y ) = W0 ⋅ ϕ (Y − E ) + ⎡⎣ F (Y ) ⎤⎦ ⋅[ A]
T
(3.11)

Les conditions aux limites sont exprimées sur les bords parallèles à x ( Y = ±σ ), où l’on peut définir des dé-
placements ou des efforts imposés.
Les expressions (2.6) permettent d’exprimer les efforts en tout point de la dalle (pour l’harmonique m) :
⎡ ρP
⎢ M x = + λ 2 (W (Y ) − ν ⋅ W (Y ) )
(0) (2)

⎢
⎢ M y = −ρ E β2 ⋅ (W (2) (Y ) − ν ⋅ W (0) (Y ) ) (3.12)
⎢
⎢Qy = −ρ E β3 ⋅ (W (3) (Y ) − α ⋅ W (1) (Y ) )
⎢
⎢Qy = −ρ E β3 ⋅ (W (3) (Y ) − (2α − ν ) ⋅ W (1) (Y ) ) = ρ E ⋅β3 ⋅ (W ( −1) (Y ) − ν ⋅ W (1) (Y ) )
⎣

La deuxième expression de Q y s’obtenant en remarquant que les fonctions ϕ( n ) et F ( n ) sont solutions de

(3.5), donc que Fi ( n + 4) (Y ) = 2α ⋅ Fi ( n + 2) (Y ) − Fi ( n ) (Y ) .
z
La relation (1.3) et la prise en compte de l’effort tran-
chant corrigé de Kirchhoff permettent d’écrire sur les t1 t2 y
bords libres :
⎛ t z ⎞ ⎛ Qy ⎞ c1 c2
⎜ ⎟ = ⎜⎜ ⎟⎟ ⋅ n y n1
⎝ cx ⎠ ⎝ − M y ⎠

cx et t z étant les densités linéiques de moments fléchis-

sants et de forces appliquées aux bords. x

En prenant n y = +1 pour le bord droit (indice 2), et n y = −1 pour le bord gauche (indice 1), on obtient :

⎛ t 2 ⎞ ⎛ Qy ( σ ) ⎞ ⎛ t1 ⎞ ⎛ −Qy ( −σ ) ⎞
⎜ ⎟ = ⎜⎜ ⎟⎟ ⎜ ⎟ = ⎜⎜ ⎟⎟
⎝ c2 ⎠ ⎝ − M y ( σ ) ⎠ ⎝ c1 ⎠ ⎝ M y ( −σ ) ⎠

Tenant compte de l’expression de la rotation en tout point ω = ∂w / ∂y = β W (1) , les déplacements et rotations
sur les deux bords s’expriment par :
⎛ W2 ⎞ ⎛ W ( σ ) ⎞ ⎛ W1 ⎞ ⎛ W ( −σ ) ⎞
⎜ ⎟=⎜ ⎟ ⎜ ⎟=⎜ ⎟
⎝ Ω2 ⎠ ⎝ βW ( σ ) ⎠ ⎝ Ω1 ⎠ ⎝ βW ( −σ ) ⎠
(1) (1)

Par commodité, les conditions aux limites seront finalement exprimées par :

⎛ t ⎞ ⎡ ( −1) ( σ ) − ν ⋅ W (1) ( σ ) ⎤
3 W ⎛ W2 ⎞ ⎛ W ( σ ) ⎞
(0)

[T2 ] = ⎜ β ⋅2c ⎟ = +ρ E ⋅β ⎢ (2) ⎥ [U 2 ] = ⎜ Ω ⎟ = ⎜⎜ (1) ⎟⎟

⎣W ( σ ) − ν ⋅ W ( σ ) ⎦ ⎝ 2 / β ⎠ ⎝ W (σ) ⎠
(0)
⎝ 2⎠
(3.13)
⎛ t ⎞ ⎡W ( −1) ( −σ ) − ν ⋅ W (1) ( −σ ) ⎤ ⎛ W ⎞ ⎛ W ( −σ ) ⎞
(0)

[T1 ] = ⎜ β ⋅1c ⎟ = −ρ E ⋅β3 ⎢ (2) ⎥ [U1 ] = ⎜ Ω /1 β ⎟ = ⎜⎜ (1) ⎟⎟

⎣ W ( −σ ) − ν ⋅ W ( −σ ) ⎦ ⎝ 1 ⎠ ⎝ W ( −σ ) ⎠
(0)
⎝ 1⎠

Il devient alors possible d’exprimer toutes les conditions aux limites à partir des valeurs des fonctions F en σ,
que l’on notera Fi ( n ) = Fi ( n ) ( σ ) , et des valeurs des fonctions F en E.

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 8

Pour ce faire, les valeurs des fonctions F en (–σ) sont transformées par les relations (3.6) :
Fi ( n ) ( −σ ) = (−1) n ⋅ Fi +( n2) ( σ ) (mod 4)

En ce qui concerne les fonctions ϕ( n ) , on montre que :

(
⎡ϕ( n ) ( σ − E ) = (−1)( n −1) sinsh ( ( n-1) µ ) ⋅ F0 ( E ) + cosch ( ( n-1) µ ) ⋅ F1 ( E )
⎢
)
⎢ϕ( n ) ( −σ − E ) =
⎢⎣ (
− sinsh ( ( n-1) µ ) ⋅ F2 ( E ) + cosch ( ( n-1) µ ) ⋅ F3 ( E ) )
Tous calculs faits, on aboutit, pour les déplacements, aux relations (I4 désigne la matrice dérivée de la ma-
trice unité en plaçant –1 au rang 4) :
⎡U ⎤
[U ] = ⎢U2 ⎥ = W0 ⋅ I4 ⋅ΦU ⋅ ⎡⎣F ( E)⎤⎦ + I4 ⋅ MU ⋅ [ A]
⎣ 1 ⎦
(3.14)
⎛Φ 0 ⎞ ⎛ 1 −r ⎞ ⎛M MU1 ⎞ ⎛ 1 0⎞ ⎛ F0 F0 ⎞
ΦU = ⎜ U 0 ⎟ ΦU 0 = ⎜ ⎟ MU = ⎜ U 0 ⎟ MU 0 = ⎜ ⎟ MU1 = ⎜ 21 31 ⎟
⎝ 0 ΦU 0 ⎠ ⎝0 1 ⎠ ⎝ MU1 MU 0 ⎠ ⎝ r 1⎠ ⎝ F2 F3 ⎠

Pour les efforts, on obtient :

⎡T ⎤
[T ] = ⎢T2 ⎥ = −W0 ⋅ρE ⋅β3 ⋅ I4 ⋅ΦF ⋅ ⎣⎡F ( E)⎤⎦ + ρE ⋅β3 ⋅ I4 ⋅ MF ⋅ [ A]
⎣ 1⎦
⎛Φ 0 ⎞ ⎛ 2r −(α − ν) ⎞
ΦF = ⎜ F 0 ⎟ ΦF 0 = ⎜ ⎟
(3.15)
⎝ 0 ΦF 0 ⎠ ⎝1 + ν r(1 − ν) ⎠
⎛M MF1 ⎞ ⎛ r(1 − ν) −(1 + ν) ⎞ ⎛ F −1 − νF21 F3−1 − νF31 ⎞
MF = ⎜ F 0 ⎟ MF 0 = ⎜ ⎟ MF1 = ⎜ 22 0 ⎟
⎝ α−ν ⎝ F2 − νF2 F3 − νF3 ⎠
0 2
⎝ MF1 MF 0 ⎠ 2r ⎠

Soit 8 équations à 4 inconnues qui permettent d’imposer 4 conditions physiquement compatibles aux bords.
Lorsque les 4 conditions imposent des valeurs nulles, on obtient les coefficients Ai par une équation de la
forme :
W0 ⋅Φ⋅ ⎡⎣F ( E ) ⎤⎦ + M ⋅ [ A] = 0 ⇒ [ A] = −W0 ⋅ G ⋅ ⎡⎣F ( E)⎤⎦ avec: G = M-1 ⋅Φ

Ce qui permet d’exprimer la solution complète :

(
W (Y ) = W0 ⋅ ϕ (Y − E ) − ⎡⎣ F (Y ) ⎤⎦ ⋅ G ⋅ ⎡⎣ F ( E ) ⎤⎦
T
) W0 =
P
4ρ E β3 r
(3.16)

D’après le théorème de Maxwell et Betti, on doit avoir W (Y , E ) = W ( E,Y ) , ce qui implique que la matrice G
soit symétrique. On vérifiera au paragraphe (3.6) ci-après que c’est bien le cas.

3.6) Calcul pratique

Lorsque les conditions aux bords sont symétriques la structure des matrices M et Φ est la suivante :
⎛ M M1 ⎞ ⎛a c⎞ ⎛d f ⎞ ⎛Φ 0 ⎞
M =⎜ 0 ⎟ M0 = ⎜ ⎟ M1 =⎜ ⎟ Φ =⎜ 0 ⎟
⎝ M1 M0 ⎠ ⎝ c' b⎠ ⎝f' e⎠ ⎝ 0 Φ0 ⎠

on peut montrer que M-1 est de la forme :

1 ⎛ ⎛ M0 M1 ⎞ ⎛ M1 M0 ⎞ ⎞
M −1 = ⋅ ⎜ D0 ⋅ ⎜ ⎟ + D1 ⋅ ⎜ ⎟⎟
D ⎜⎝ ⎜ M1 M 0 ⎟⎠ ⎜ M0 M1 ⎟⎠ ⎟⎠
⎝ ⎝

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 9

Avec :
D0 = ab − cc '+ de − ff '
⎛ b −c ⎞ ⎛ e −f ⎞
M0 = ⎜ ⎟ M1 = ⎜ ⎟ D1 = fc '− ae + cf '− bd
⎝ −c ' a ⎠ ⎝− f ' d ⎠ D = ( D0 + D1 )( D0 − D1 )

Donc, G est de la forme :

1 ⎛ ⎛ G0 G1 ⎞ ⎛ G1 G0 ⎞ ⎞ ⎡G = M 0 ⋅ Φ 0
G= ⋅ ⎜ D0 ⎜ ⎟ + D1 ⎜ ⎟⎟ avec : ⎢ 0
D ⎝ ⎝ G1 G0 ⎠ ⎝ G0 G1 ⎠ ⎠ ⎢⎣ G1 = M1 ⋅ Φ 0

Après calculs, on trouve :

− pour une dalle avec deux bords libres :

⎡
⎡
⎢
⎛ − (1 + ν )2 − 4r 2
⎜ ( 2
)
r (1 − ν ) + 2 ( α − 1) ⎞
⎟
⎢ H = 4r − (1 + ν )
2
⎢G 0 = ⎜
2

⎢ D = H 1 − e −4 r σ
⎢ 0 ( ) ⎢ ⎝ ( )
⎜ r (1 − ν ) + 2(α − 1) − r (1 − ν ) − ( α − ν ) ⎟
2 2 2 2 ⎟

⎠
⎢
⎢
( )
⎢⎣ D1 = 2r (1 − ν ) + 2 ( α − 1) ( − F3 )
⎢ ⎛ F3 − F2 ⎞
1 1
2 0
⎢G1 = H ⋅ ⎜⎜ 1 1⎟
⎟
⎢⎣ ⎝ − F2 ( α − 1) / 2 ⋅ F3 ⎠

− pour une dalle avec deux bords appuyés :

⎡ H = −2r
⎢ ⎛ 2r −2r 2 ⎞ ⎛ F1 − F21 ⎞
⎢ D0 = 2r ⋅ (1 + e )
−4 r σ
G 0 = ⎜⎜ ⎟ G1 = H ⋅ ⎜⎜ 3 1 1⎟
⎢ ⎝ −2r
2
( α − 1) ⋅ r ⎟⎠ ⎝ − F2 ( α − 1) / 2 ⋅ F3 ⎟⎠
⎣ D1 = −4r ⋅ F2
0

− pour une dalle avec deux bords encastrés :

⎡H = 1
⎢ −4 r σ ⎛1 −r ⎞ ⎛ F1 − F21 ⎞
⎢ D0 = 1 − e G0 = ⎜
− +
⎟ G1 = H ⋅ ⎜⎜ 3 1 ⎟⎟
( α − 1) / 2 ⋅ F ⎠
r2 ⎠ ⎝ − F2
1
⎝ r 1
⎢⎣ D1 = 2r ⋅ F30 3

Ce qui confirme bien le caractère symétrique de G. En outre, deux observations traduisant les propriétés phy-
siques du système sont intéressantes :
− D1 et G1 tendent rapidement vers zéro avec σ, ce qui a pour effet de rendre indépendantes les conditions
aux limites sur chacun des bords pour σ élevé, c’est à dire pour les harmoniques élevés.
− Pour une dalle avec deux bords libres, les termes diagonaux de la matrice G0 sont négatifs, contrairement
aux cas d’une encastrée. D’après (3.16), cela reflète qualitativement le fait qu’une dalle à bords libres
prend des flèches plus importantes que la dalle infiniment large ayant servi à établir la solution particu-
lière, et inversement pour une dalle encastrée.

4) Expressions de la déformée et des efforts

Nous adopterons à partir d’ici les conventions de signe habituelles de la R.D.M., à savoir σ > 0 pour les
compressions, ce qui revient à changer de signe tous les efforts internes.
y L
z Reprenons le chargement de référence (3.1),
mais avec des coefficients négatifs, afin que le
chargement externe, vertical descendant, soit
2b e positif.
x
∞
mπx
P ( x ) = −∑ Pm ⋅ sin
m =1 L

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 10

Pour les flèches, la solution générale est donnée par (3.16) pour chaque harmonique, l’expression de la ma-
trice G étant à choisir parmi celles données au paragraphe (3.6), en fonction des conditions d’appui aux
bords :

Wm (Ym , Em ) = −
Pm
4ρ E βm r
3 (
⋅ ϕ (Ym − Em ) − ⎡⎣ F (Ym ) ⎤⎦ ⋅ G m ⋅ ⎡⎣ F ( Em ) ⎤⎦
T
)
En posant :

W m (Ym , Em ) = ϕ (Ym − Em ) − ⎡⎣ F (Ym ) ⎤⎦ ⋅ G m ⋅ ⎡⎣ F ( Em ) ⎤⎦

T
(4.1)

la solution de l’équation fondamentale (3.2) peut être écrite, pour l’harmonique m :

βm λ m4
wm ( x, y, e ) = − Pm ⋅ ⋅ W m (Ym , Em ) ⋅ sin X m (4.2)
4ρ P r

Les efforts en tout point de la dalle sont donnés par (3.12) (en tenant compte du changement de signe des
efforts internes) :
⎡
⎢ M xm = Pm ⋅
⎢
βm λ m2
4r
(0)
(
⋅ W m (Ym , Em ) − ν ⋅ W m (Ym , Em )
(2)
) ⋅ sin X m

⎢ 1
(
⎢ M ym = − Pm ⋅ 4rβ ⋅ W m (Ym , Em ) − ν ⋅ W m (Ym , Em )
(2) (0)
) ⋅ sin X m
⎢ m (4.3)
⎢
⎢Qym =
⎢
1
4r
(
− Pm ⋅ ⋅ W m (Ym , Em ) − α ⋅ W m (Ym , Em )
(3) (1)
) ⋅ sin X m

⎢Q =
⎢⎣ ym
1
(
( −1)
Pm ⋅ ⋅ W m (Ym , Em ) − ν ⋅ W m (Ym , Em )
4r
(1)
) ⋅ sin X m

5) Coefficients de Guyon – Massonnet

Comme il a été dit dans l’introduction, ainsi que dans la préface de [1], la méthode de Guyon–Massonnet
(qui ne s’applique qu’aux dalles à bords libres) est basée sur des « coefficients de répartition », publiés sous
forme d’abaques, dont les plus connus sont le coefficient K, « coefficient de répartition transversale », et le
coefficient µ, « coefficient de calcul des moments fléchissants transversaux ».
Bien que l’utilisation de ces coefficients ne soit pas indispensable dans le cadre de la présente étude, entiè-
rement basée sur des expressions analytiques explicites, elle présente de l’intérêt à plusieurs titres :
− la méthode est souvent utilisée pour des ouvrages hyperstatiques, avec application du coefficient K à mi-
portée à l’ensemble de la travée,
− donner des expressions simples de ces coefficients, encore très utilisés,
− enfin, valider les résultats obtenus.

5.1) Flèches et moments longitudinaux

La méthode du coefficient de répartition transversale K, consiste à comparer la déformée w( x, y ) et les mo-

ments M x ( x, y ) en un point d’une dalle soumise à une charge de type « couteau », comme celle du paragra-
phe (4) ci-dessus avec la déformée w0 ( x) et les moments M x 0 ( x) que cette même charge provoquerait si
elle était uniformément répartie sur toute la largeur de la dalle. Rappelons rapidement le raisonnement, trans-
posé dans le contexte du présent article :
− On intègre (4.2) sur la largeur de la dalle pour obtenir la « flèche moyenne » pour la charge couteau :
σ
λ 4m m

w0 m ( x, e ) = − Pm ⋅ ⋅ ∫ W m (Ym , Em ) ⋅ dYm ⋅ sin X m

4ρ P r −σm

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 11

− On définit K de sorte que :
wm ( x, y , e ) W m (Ym , Em )
K m ( y, e ) = =
w0 m ( x, e ) σm

βm ⋅ ∫ W (Y
−σm
m m , Em ) ⋅ dYm

D’où résulte la propriété :

b
1
K m ( y, e ) ⋅ d y = 1
2b −∫b

Ainsi que la propriété de symétrie, en raison du théorème de Maxwell et Betti et de la démonstration du pa-
ragraphe (3.6) :
K m ( y, e ) = K m ( e, y )

Une autre propriété fondamentale provient de l’expression (4.1), où les fonctions φ et F et la matrice Gm ne
y e
dépendent que de α, ν , σm = mπθ , Ym = mπθ et Em = mπθ , ce qui signifie que :
b b
⎛ e y⎞ ⎛ e y⎞
K m ⎜ α, ν, θ, , ⎟ = K1 ⎜ α, ν, mθ, , ⎟
⎝ b b⎠ ⎝ b b⎠

ce qui constitue une condition indispensable pour pouvoir travailler avec plusieurs harmoniques sur la base
d’abaques.
Comme il a été dit au paragraphe (2), la formulation du problème par Guyon et Massonnet, essentiellement
axée sur les grillages de poutres, néglige explicitement l’influence du coefficient de Poisson. Dans ce cas,
(4.2) et (4.3) montrent que l’on peut indifféremment raisonner sur la flèche ou sur le moment de flexion lon-
gitudinal, qui sont proportionnels. Il en résulte qu’un seul coefficient K, conforme à la définition ci-dessus,
est suffisant.
Dans la présente étude, où aucune hypothèse restrictive n’est faite sur le coefficient de Poisson, on est amené
à introduire deux coefficients K, l’un pour les flèches et l’autre pour les moments longitudinaux.
Pour ce faire, on prendra comme élément de référence non pas la dalle elle-même, mais la poutre de même
longueur et de même rigidité de flexion soit 2b ⋅ ρ P . En effet, si on place la charge de façon uniformément
répartie sur la largeur 2b de la dalle, la déformée n’est plus indépendante de y dans le cas général, ce qui rend
la notion de « flèche moyenne » délicate à manipuler.
Sous l’effet de la charge P(x), il est facile de montrer que la poutre de référence prend une déformée et est
soumise à un moment par unité de largeur :
λ 4m λ m2
w0 m ( x ) = − Pm ⋅ sin X m M 0 m ( x ) = Pm ⋅ sin X m (5.1)
2b ⋅ ρ P 2b

ce qui permet d’introduire les deux coefficients de répartition transversale :

wm ( x, y , e ) σm
K wm ( y, e ) = = ⋅ W m (Ym , Em )
w0 m ( x ) 2r
(5.2)
M ( x, y , e ) σ m
K Mm ( y , e ) = xm
M 0m ( x )
=
2r
(
⋅ W m (Ym , Em ) − ν ⋅ W m (Ym , Em )
(2)
)

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 12

On notera que dans le cas général (coefficient de Poisson non nul), les propriétés relatives au coefficient K de
Guyon et Massonnet se « répartissent » entre K wm et K Mm :

K wm ( y, e ) = K wm ( e, y ) K Mm ( y, e ) ≠ K Mm ( e, y )
b b
1 1
K wm ( y, e ) ⋅ d y ≠ 1 K Mm ( y, e ) ⋅ d y = 1
2b −∫b 2b −∫b

La dernière égalité, physiquement évidente, est due au fait que la somme des moments longitudinaux sur la
largeur de la dalle est égale au moment total. Il est néanmoins utile de la démontrer à titre de vérification des
calculs formels, ce qui revient, pour un harmonique donné, à :

( )
σ
1
W (Y , E ) − ν ⋅ W (Y , E ) ⋅ dY = 1
(2)
∫
4r −σ

En utilisant l’expression (4.1) de W et la propriété d’intégration (3.10) des fonctions φ, on voit que cela
revient à montrer :
σ
⎡W ( −1) (Y , E ) − ν ⋅ W (1) (Y , E ) ⎤ = 0
⎢⎣ ⎥⎦ −σ

ce qui résulte directement des conditions aux limites t1 = 0 et t2 = 0 dans les expressions (3.13).

5.2) Moments transversaux

Puisque, contrairement au cas des moments longitudinaux, il n’existe pas de grandeur simple de comparai-
son, le « coefficient de calcul des moments fléchissants transversaux » est directement défini par :
mπx
M ym ( x, y, e) = Pm b ⋅ µ m ( y, e) ⋅ sin (5.3)
L
Ce qui donne immédiatement par (4.3) :

µ m ( y , e) = −
1
4r σ m
(W m (Ym , Em ) − ν ⋅ W m (Ym , Em )
(2)
) (5.4)

5.3) Tests numériques

Des tests numériques intensifs de comparaison avec les résultats publiés dans [1] ont été effectués :
− tables donnant K et µ pour ν = 0 et α = 0 , α = 1 ,
− tables donnant K et µ pour ν = 0,15 et α = 1 ,
− expression analytique de K et µ pour α = 1 et ν quelconque.

Il en résulte, dans le cas α = 1 , une parfaite concordance entre le coefficient K de Guyon–Massonnet et le

coefficient K w donné ci-dessus, ainsi qu’entre les coefficients µ obtenus par les deux méthodes. Dans le cas
α = 0 , un peu plus complexe numériquement, de légères différences aléatoires ne dépassant jamais 10-3 ont
été constatées.
On peut en outre noter qu’en toute rigueur les valeurs de K publiées par ces auteurs pour ν ≠ 0 ne
s’appliquent qu’aux flèches et sont légèrement fausses pour les moments, l’expression à utiliser étant alors
l’expression de K M donnée ci-dessus. Il en va en particulier ainsi pour les tables et les formules analytiques
données pour les dalles isotropes.

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 13

6) Effets de différents types de charges
On reprendra ici, à titre d’illustration, les résultats classiques que l’on obtient pour une charge linéique et une
charge rectangulaire constantes.
De par la nature même de la méthode, ces résultats peuvent être étendus sans difficulté à toute les charges
linéiques développables en série de Fourier. En outre, les propriétés d’intégration (3.10) permettent aussi de
traiter facilement le cas de charges surfaciques d’intensité linéairement variable suivant y, qui est un cas que
l’on rencontre fréquemment dans les calculs de poids propre.

6.1) Charge linéique constante

z y 2c La décomposition en série de Fourier, sur un intervalle de
longueur L, d’une charge totale P d’étalement 2c, centrée
sur la section d, est donnée par :
e ∞
2 mπc mπd mπx
d
x P ( x) = − P ∑ ⋅ sin ⋅ sin ⋅ sin
m =1 mπc L L L

que l’on notera :

mπc
sin
2P ∞ mπx L ⋅ sin mπd ⎛ lim a = sin mπd ⎞
P ( x) = − ∑
L m =1
am ⋅ sin
L
am =
mπc L ⎝
⎜ c →0 m
L ⎠
⎟
L

Les expressions (5.1), (5.2) et (5.3) donnent immédiatement :

PL3 ∞
am mπx
w ( x, y , e ) = −
bρ P π4
∑m
m =1
4
K wm ( y, e ) ⋅ sin
L
PL ∞
am mπx
M x ( x, y , e ) =
bπ 2
∑m
m =1
2
K Mm ( y, e ) ⋅ sin
L
(6.1)

2 Pb ∞
mπx
M y ( x, y , e ) =
L
∑
m =1
am µ m ( y, e ) ⋅ sin
L

6.2) Charge rectangulaire constante

Il suffit d’intégrer entre e1 et e2 la charge linéique. P représentant toujours le poids total de la charge, on a :

PL3 a ∞ ⎛ e2 mπx ⎞
w ( x, y , e ) =
bρ P π4 ( e2 − e1 )
∑ m ⎜⎜ ∫ K ( y, e ) ⋅ de ⎟⎟ ⋅ sin L
m
4 wm
m =1 ⎝ e1 ⎠
PL a ∞ ⎛ e2
mπx ⎞
M x ( x, y , e ) =
bπ ( e2 − e1 )
2 ∑ m ⎜⎜ ∫ K ( y, e ) ⋅ de ⎟⎟ ⋅ sin L
m
2 Mm
m =1 ⎝ e1 ⎠
2 Pb ∞ ⎛ e2
⎞
mπx
M y ( x, y , e ) =
L ( e2 − e1 )
∑ a ⎜⎜ ∫ µ ( y, e ) ⋅ de ⎟⎟ ⋅ sin L
m m
m =1 ⎝ e1 ⎠

Toutefois, ces formules faisant intervenir des intégrales définies, il convient de tenir compte des remarques
développées au paragraphe (3.4) et de remplacer dans l’expression de W la fonction ϕ( −1) par la fonction
ϕ(I −1) .

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 14

7) Comparaison avec un calculateur à barres
Le recoupement de la méthode de Guyon–Massonnet avec un calculateur à barres présente un double intérêt :
− évaluer les différences entre la modélisation par un grillage de poutres et la modélisation par la théorie
des dalles orthotropes ;
− explorer la validité du domaine α > 1, qui n’a pas été considéré comme physiquement représentatif par
MM. Guyon et Massonnet (bien qu’il s’agisse de l’argument « officiellement » avancé, nous pensons
plutôt que les auteurs n’ont pas voulu compliquer la méthode en doublant le volume des expressions ma-
thématiques, déjà très complexes) ;

Naturellement, compte tenu du caractère « filaire » des barres, seul le cas ν = 0 a pu être modélisé.
Le programme utilisé est le programme ST1 du Sétra qui, par la grande richesse de son langage de comman-
des permet d’effectuer facilement des études paramétriques. Le grillage utilisé comporte 21 poutres et 17
entretoises. Afin de restreindre le nombre considérable de comparaisons possibles, seuls ont été étudiés :
− les moments longitudinaux M x dans la section médiane de chaque poutre, ramenés au mètre de largeur
de la dalle, soit 21 résultats pour chaque cas de charge,
− les moments « transversaux » M y , représentés par les moments longitudinaux de l’entretoise médiane,
ramenés au mètre de longueur de la dalle.
En outre, pour améliorer la représentativité du modèle, deux précautions ont été prises :
− Affecter la rigidité de torsion uniquement aux entretoises afin d’éviter les discontinuités de moment
transversal au droit des poutres (dans le modèle de la plaque orthotrope seul intervient γ P + γ E ). Cette
précaution présente en particulier comme avantage d’obtenir M y = 0 aux deux extrémités de l’entretoise.

− Corriger les moments dans les poutres, qui sont des moments discrets, par le facteur :
M xt 21
ρ= avec : M xt = ∑ M i
M + M 21
M xt − 1 i =1
2
de sorte que l’intégrale du diagramme continu évaluée par la méthode des trapèzes soit égale à M xt .

7.1) Charges sinusoïdales

La première comparaison à effectuer porte bien évidemment sur chaque terme des séries de Fourier, soit sur
les charges de la forme :
mπx
P ( x) = Pm ⋅ sin
L
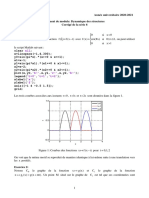
À titre d’exemple, les graphiques ci-après illustrent les résultats donnés par la méthode de Guyon–Massonnet
(ligne continue) et ceux données par le calculateur à barres (points discrets). Ils donnent les coefficients K1 et
µ1 à mi-portée de la dalle, pour une charge placée respectivement sur l’axe, aux trois quarts et sur le bord de
la dalle, en mettant en évidence l’influence du paramètre de torsion (α = 0, 1, 2).
On peut constater que les deux méthodes se recoupent en général de façon excellente. Les moins bons résul-
tats sont obtenus pour les moments transversaux engendrés par une charge placée en bord de dalle avec
α = 0, ce qui s’explique aisément : en bord de dalle, le modèle à barres possède une poutre, qui résiste direc-
tement à la charge, alors que, dans le modèle « plaque », il est nécessaire de faire contribuer une certaine
largeur de dalle pour reprendre ces mêmes efforts.

Ce phénomène s’atténue d’ailleurs rapidement lorsque α croît, c’est-à-dire lorsque les entretoises travaillent
en torsion et minimisent l’influence de la poutre de rive.

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 15

 K (α = 0) µ (α = 0)

K (α = 1) µ (α = 1)

K (α = 2) µ (α = 2)

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 16

Ces résultats permettent d’établir deux points importants :
− la modélisation d’une plaque orthotrope par un grillage de poutres est tout à fait légitime (et réciproque-
ment) ;
− les résultats trouvés pour α > 1 sont en très bon accord avec le modèle à barres.

7.2) Charges ponctuelles

D’autres comparaisons entre les deux modèles ont également été effectuées sur des charges ponctuelles, ri-
ches en harmoniques de rang élevé, afin d’étudier les conditions de convergence.
Pour n harmoniques, on obtient des grandeurs adimensionnelles et facilement comparables aux résultats don-
nés par le modèle à barres à l’aide des relations (5.1) et (6.1) :
n
am mπx
M ( x, y , e ) ∑ m
K ( y , e ) ⋅ sin
2 m
L
Kn ( x, y , e ) = xn
= m =1

M ( x) a n
mπx
0n
∑ m ⋅ sin L
m =1
m
2

L n
mπx
µ n ( x, y , e ) = M yn ( x, y, e) = ∑ am µ m ( y , e) ⋅ sin
2 Pb m =1 L

Les graphiques ci-après illustrent les résultats obtenus pour n = 50 avec une charge placée en milieu de tra-
vée, dans des conditions identiques aux charges sinusoïdales étudiés en (7.1).
On constate là-encore que le modèle à barres donne des résultats très acceptables, excepté pour les pics situés
au droit de la charge, qui ne peuvent être totalement mis en évidence en raison de la discrétisation (il est fa-
cile de voir que la série donnant µn est divergente en y = e).
En comparant avec les résultats obtenus pour les charges sinusoïdales, on constate également que l’on com-
met une erreur très importante en affectant à ce type de charges le seul coefficient K1, comme c’est quelque-
fois le cas.

K (α = 1) µ (α = 1)

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 17

 DEUXIÈME PARTIE : ÉTUDE D’UN ENSEMBLE DE DALLES CONTIGUËS
La première partie de cette étude a permis de généraliser la méthode de Guyon – Massonnet aux dalles rec-
tangulaires orthotropes simplement appuyées sur deux bords opposés de sorte à s’abstraire :
− des limitations sur le coefficient de Poisson ν et le coefficient de torsion α,
− de l’obligation que les deux autres bords de la dalle soient libres.
La clé de cette généralisation réside essentiellement dans l’expression (4.1), exprimant la « flèche réduite »
de la dalle :
⎛ F0 ( E ) ⎞
⎜ ⎟
⎜ F1 ( E ) ⎟
W (Y , E ) = ϕ(Y − E ) − ( F0 (Y ) , F1 (Y ) , F2 (Y ) , F3 (Y ) ) ⋅ G ⋅
⎜ F2 ( E ) ⎟
⎜⎜ ⎟⎟
⎝ F3 ( E ) ⎠

Cette expression, très simple et très facilement dérivable ou intégrable, permet d’exprimer aisément les ef-
forts internes dans la dalle, ainsi que les flèches et les rotations.
Cette dernière propriété a été jugée intéressante à explorer dans la mesure où elle permet de relier les char-
gements appliqués sur les bords « libres » aux déplacements de ces mêmes bords, c’est-à-dire de calculer la
« matrice de rigidité » de la dalle. Il est ainsi possible d’étudier, par des méthodes strictement analogues à
celles des programmes à barres, plusieurs dalles contiguës de caractéristiques différentes reliées entre elles.
Le principal intérêt de cette approche est de permettre l’étude de tabliers du type ponts à nervures ou ponts à
poutres, en bénéficiant simultanément des résultats relatifs à la flexion générale et à la flexion locale.

8) Matrice de rigidité d’une dalle orthotrope

Plaçons nous dans le cas d’une dalle non chargée et cherchons à exprimer les efforts à appliquer sur les bords
de la dalle en fonction des déplacements de ceux-ci. Avec W0 = 0 , les relations (3.14) et (3.15) donnent :

[T ] = ρE ⋅β3 ⋅ I4 ⋅ MF ⋅ MU-1 ⋅ I4 ⋅ [U ] (8.1)

L’algorithme vu au paragraphe (3.6) permet d’exprimer MF ⋅ MU−1 sous la forme :

1 ⎛ MF0 M F 1 ⎞ ⎛ ⎛ MU 0 MU 1 ⎞ ⎛ MU 1 MU 0 ⎞ ⎞
M F ⋅ MU-1 = ⋅⎜ ⎟ ⋅ ⎜ D0 ⎜ ⎟ + D1 ⎜ ⎟⎟
D ⎝ M F1 M F 0 ⎠ ⎜ ⎜⎝ MU 1 MU 0 ⎟⎠ ⎜ MU 0
⎝ MU 1 ⎟⎠ ⎟⎠
⎝

D0 et D1 étant les mêmes que pour la dalle avec deux bords encastrés. Il s’ensuit que (8.1) s’exprime par :

1 ⎛ ⎛ R R1 ⎞ ⎛ R1 R0 ⎞ ⎞ ⎡R0 = MF 0 ⋅ MU 0 + MF1 ⋅ MU1

[T ] = ρE ⋅β3 ⋅ I4 ⋅ ⎜ D0 ⋅ ⎜ 0 ⎟ + D1 ⋅ ⎜ ⎟ ⎟ ⋅ I4 ⋅ [U ] avec: ⎢
D ⎝ ⎝ R1 R0 ⎠ ⎝ R0 R1 ⎠ ⎠ ⎣⎢R1 = MF 0 ⋅ MU1 + MF1 ⋅ MU 0

Tous calculs faits, on trouve :

D0 = 1 − e −4 rσ D1 = 2r ⋅ F3(0)
⎛ 2r (1 + e −4 rσ ) −(1 + ν ) (1 − e −4 rσ ) ⎞ ⎛ 2 F2(0) (1 − ν ) F3(0) ⎞
R0 = ⎜ ⎟ R1 = −2r ⋅ ⎜ ⎟
⎜ −(1 + ν ) (1 − e −4 rσ ) 2 r (1 + e −4 r σ
) ⎠ ⎟ ⎝ (1 − ν ) F3
(0)
−2 F2(0) ⎠
⎝

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 18

ce qui permet finalement d’exprimer la matrice de rigidité pour chaque harmonique sous la forme :
⎛ T1 ⎞ ⎛ β2 a −β c β2 d β f ⎞ ⎛ W1 ⎞
⎜ ⎟ ⎜ ⎟⎜ ⎟
⎜ C1 ⎟ = ρ β ⋅ ⎜ −βc b −β f −e ⎟ ⎜ Ω1 ⎟ (8.2)
⎜ T2 ⎟ E
⎜ β2 d −β f β2 a β c ⎟ ⎜ W2 ⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎜ ⎟
⎝ C2 ⎠ ⎝ βf −e βc b ⎟⎠ ⎜⎝ Ω 2 ⎟⎠

qui ne dépend que de 6 coefficients a, b, c, d, e, f.

9) Assemblage des matrices de rigidité de plusieurs dalles

Considérons plusieurs dalles contiguës reliées entre C0 Ci Cn
elles et supposons que cet assemblage est soumis à
chaque nœud de jonction à des chargements T0, C0,
T1, C1, …, suivant la figure ci-contre. 1 i i+1 n
T0 Ti Tn

On suppose également que des « poutres additionnel- ⎛ EI ⎞

⎜ 4 0 ⎟
les » peuvent être disposées à chaque nœud, avec des ⎛ T ⎞ ⎜ λm ⎟ ⋅ ⎛ Wi,m ⎞
P

⎟⎟ = ⎜
i ,m
matrices de rigidité : ⎜⎜ ⎜ ⎟
P
⎝C ⎠ ⎜ 0
i ,m GK ⎟ ⎝ Ωi,m ⎠
⎜ ⎟
⎝ λ2m ⎟⎠

Le chargement du nœud i, développé en série de Fourier, se répartit entre la poutre et les dalles i et i+1 :
Ti,m = Ti,Pm + T2,Di,m + T1,Di+1,m
Ci,m = CiP,m + C2,Di,m + C1,Di+1,m

En imposant la continuité de la flèche et de la rotation ⎛ T0,m ⎞ ⎛ W0,m ⎞

à chaque jonction entre dalles on peut donc, pour cha- ⎜ ⎟ ⎜ ⎟
⎜ C0,m ⎟ ⎜ Ω0,m ⎟
que harmonique, assembler de façon très classique les ⎜ ... ⎟ = Rm ⋅ ⎜ ... ⎟ (9.1)
matrices de rigidité (8.2) de chaque dalle pour obtenir ⎜ ⎟ ⎜ ⎟
la matrice de rigidité globale sous la forme ci-contre. ⎜ Tn,m ⎟ ⎜ Wn,m ⎟
⎜C ⎟ ⎜Ω ⎟
⎝ n,m ⎠ ⎝ n,m ⎠

On obtient ainsi une matrice de rigidité globale pour chaque harmonique, dont la principale propriété est de
posséder une « largeur de bande » très faible et constante, égale à 4. Le temps d’inversion de l’ensemble des
matrices de rigidité est donc simplement proportionnel au nombre d’harmoniques et au nombre de plaques.
En pratique, cela signifie qu’il n’est pas nécessaire de restreindre la finesse du modèle pour obtenir des temps
de calcul acceptables.

10) Étude d’un tablier formé de plusieurs dalles contiguës

Considérons maintenant que l’ensemble de dalles
défini au paragraphe (9) forme une travée isostatique
supportant des charges extérieures données.
1 i i+1 n

Suivant la méthode classique de relaxation des nœuds, il est possible d’étudier séparément chacune des dalles
avec le chargement qui lui est directement appliqué et en supposant que ses bords sont bi-encastrés (système
A).
On tire de cette étude les réactions d’appui nécessaires pour assurer l’encastrement de chaque dalle : T1,i, C1,i,
T2,i, C2,i, …, ainsi que la déformée et les efforts internes qu’elle subit, ce qui revient à connaître la fonction de
déplacement WA (Y ) pour chaque harmonique et pour chaque dalle.

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 19

 C1,i C2,i C1,i+1 C2,i+1 –C2,i-1–C1,i –C2,i–C1,i+1 –C2,i+1–C1,i+2

i i+1 i i+1

T1,i T2,i T1,i+1 T2,i+1 –T2,i-1–T1,i –T2,i–T1,i+1 –T2,i+1–T1,i+2

Système A Système B

Étudions maintenant la même structure, mais uniquement soumise à l’opposé des réactions d’appui calculées
ci-dessus (système B).
L’inversion du système (9.1) permet de trouver le déplacement et la rotation des bords de chaque dalle soit,
en reprenant les notations du paragraphe (3.5) :
⎛ Wi , m ⎞ ⎛ Wi −1, m ⎞
[U 2 ] = ⎜ Ω ⎟ [U1 ] = ⎜ Ω ⎟
⎝ i , m / βi , m ⎠ ⎝ i −1,m / βi , m ⎠

Dans le système B, chaque dalle est donc une dalle non chargée soumise aux conditions aux limites U2, U1.
L’équation (3.14) permet de trouver les coefficients Ai de la fonction de déplacement sous la forme :
⎡U ⎤
[ A] = I4 ⋅ M−1 ⋅ ⎢U2 ⎥
⎣ ⎦
U
1

MU−1 est calculable par l’algorithme du paragraphe (3.6), ce qui permet par (3.11) d’exprimer la fonction dé-
placement du système B pour chaque harmonique et pour chaque dalle :
⎡U ⎤
WB (Y ) = ⎡⎣ F (Y ) ⎤⎦ ⋅I 4 ⋅ M −U1 ⋅ ⎢ 2 ⎥
T

⎣U 1 ⎦

Enfin, de façon très classique, la superposition des systèmes A et B donne la fonction de déplacement de
chaque dalle dans la configuration réelle :
W (Y ) = WA (Y ) + WB (Y )

ce qui résout entièrement le problème, puisque la fonction déplacement donne accès à l’ensemble des efforts
internes dans chaque dalle.
L’une des premières questions qui se posent est de savoir si ce modèle est compatible avec le modèle à dalle
unique, autrement dit, de savoir si les résultats obtenus sont identiques pour une dalle seule et la même dalle
modélisée sous forme d’une juxtaposition de dalles de mêmes caractéristiques.
Or, entre deux dalles adjacentes, nous avons imposé la continuité de la flèche, et de la rotation, ce qui impli-
que la continuité de :
∂n w ∂w
∀n et :
∂x n ∂y

Nous avons également imposé la continuité de M y et de l’effort tranchant corrigé de Kirchhoff Q y . On voit
∂2w ∂3w
alors par (2.6) que cela impose la continuité de et de , soit de tous les efforts internes dans les dal-
∂y 2 ∂y 3
les, résultats qui ont été parfaitement confirmés par des tests numériques.
En définitive, cette méthode s’est avérée très puissante et permet d’abandonner la modélisation classique, où
l’ensemble du tablier est considéré comme une « gigantesque » dalle orthotrope, au profit d’une modélisation
plus fine où les poutres, nervures, hourdis, peuvent être considérés comme des éléments autonomes.

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 20

11) Exemple d’un tablier à deux nervures larges
Des comparaisons numériques ont été effectuées par G. Lacoste, V. Le Khac et N. Van Ké, du Sétra, entre la
méthode du paragraphe (10) et des calculs aux éléments finis sur différents types de tabliers. Nous présen-
tons ci-après, à titre d’exemple, les résultats obtenus sur un tablier à deux nervures larges de 25 mètres de
portée, dont la coupe transversale est la suivante :

A B C

h =1,00
d = 0,22

1,50 Ln = 2,50 4,00 Ln = 2,50 1,50

Une charge de 15 t et d’impact 0,50 m × 0,50 m est successivement placée au milieu de l’encorbellement
gauche, au milieu de la nervure gauche et au milieu du hourdis central (A, B, C).
On adopte : E = 200 000 MPa, ν = 0,20.

11.1) Modélisation par la méthode de Guyon – Massonnet

Nous passerons rapidement sur le calcul des caractéristiques :

− Les portions de hourdis sont considérées comme des dalles isotropes infinies (cf. [1]) :
E d3
ρP = ρE = ⋅ = 36,9722 MN ⋅ m
1 − ν 2 12
d3
γP = γE = G ⋅ = 29,5778 MN ⋅ m
6
− Longitudinalement, les nervures sont également considérées comme des dalles infinies :
E h3
ρE = ⋅ = 3472, 2222 MN ⋅ m
1 − ν 2 12
h3
γE = G ⋅ = 2777,7778 MN ⋅ m
6
− Transversalement, l’inertie de flexion des nervures est calculée de telle sorte que l’inertie totale du tablier
soit conservée en considérant que le hourdis est centré sur l’axe neutre et l’inertie de torsion est celle du
rectangle constituant la nervure ramenée à l’unité de longueur, ce qui donne :
E I
I n = 0, 2979 m 4 ρE = ⋅ n = 4964,5387 MN ⋅ m
1 − ν Ln
2

Jn
J n = 0,6198 m 4 γE = G ⋅ = 4132,1767 MN ⋅ m
Ln

Il apparaît ainsi que les nervures ne peuvent pas être réduites à de simples dalles isotropes, ce qui conserve
tout l’intérêt de l’analyse relative aux dalles orthotropes. Bien qu’ils n’interviennent pas dans le calcul, on
peut calculer les coefficients de Poisson correspondants en x et y :
ρP ρE
νx = ν ⋅ = 0, 293 νy = ν ⋅ = 0,167
ρE ρP

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 21

11.2) Modélisation par éléments finis

L’étude a été menée avec le programme Systus. La travée est modélisée par 19392 éléments de coque spa-
tiale à 6 degrés de liberté par nœud, avec un pas transversal de 12,5 cm.

11.3) Comparaison

Les graphiques ci-après montrent, pour les trois cas de charge, l’excellente concordance entre la modélisation
par la méthode de Guyon – Massonnet (trait continu) et le calcul aux éléments finis (points discrets).

Charge au milieu de l’encorbellement

Moment longitudinal Moment transversal

Charge au milieu de la nervure

Moment longitudinal Moment transversal

Charge au milieu du hourdis central

Moment longitudinal Moment transversal

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 22

12) Conclusion
La méthode de « Guyon – Massonnet » a été conçue à l’origine dans le but de donner un outil de calcul effi-
cace aux ingénieurs, à une époque où les moyens de calcul automatique étaient encore très peu développés.
Cela explique que le souci majeur de leurs auteurs ait été de produire des abaques et non de raffiner inutile-
ment une théorie sans en attendre de retombées pratiques.
Toutefois, malgré ses hypothèses restrictives (travée droite sur appuis simples), cette méthode est suffisam-
ment puissante et générale pour conserver un intérêt dans le cadre des moyens de calculs actuels et elle méri-
tait donc à ce titre d’être réactualisée.
Sur la base de la nouvelle formulation présentée dans cet article, il a été possible de montrer que la méthode
pouvait être largement généralisée et affinée, et qu’elle permettait de mettre au point des moyens de calcul
simples et aux résultats directement exploitables, susceptibles de satisfaire la plupart des besoins courants
relatifs à l’étude de la flexion transversale.
Ces améliorations donnent notamment accès à une modélisation individuelle de chaque constituant du tablier
(poutres, nervures, hourdis) et permettent d’obtenir directement les efforts dans chacune de ces parties, en-
corbellements compris, sans qu’il soit nécessaire de distinguer les traditionnels effet de flexion générale et de
flexion locale.

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 23

Bibliographie
[1] R. Barès, C. Massonnet − Le calcul des grillages de poutres et dalles orthotropes selon la méthode Guyon–
Massonnet– Barès. Dunod, 1966.
[2] S. Timoshenko − Théorie des plaques et coques. Librairie Polytechnique Ch. Beranger, 1961.
[3] J. Courbon − Résistance des Matériaux. Dunod, 1964. Tome I, ch. XXIX.
[4] C. Massonnet − Compléments à la méthode de calcul des ponts à poutres multiples. Annales de l’ITBTP, janvier
1962, n°169.

Nouvelle formulation de la méthode de MM. Guyon et Massonnet – page : 24